基于神经网络的柳林地区煤储层渗透率预测方法

汪雷, 汤达祯, 许浩, 孟艳军, 喻廷旭, 陈林

(1.中国地质大学(北京)能源学院, 北京 100083; 2.西南石油大学地球科学与技术学院, 四川 成都 610500)

0 引 言

中国煤层气资源丰富,分布广泛,共计42个主要含气盆地,其中埋深2 000 m以浅煤层气地质资源量36.8×1012m3,埋深1 500 m以浅煤层气可采资源量10.9×1012m3。煤层气的运移和产出都与煤层渗透性有极大的关系,表征渗透性的量为渗透率。在煤层气勘探过程中,渗透率是资源评价和开发选区的重要参数;在探明煤层气资源量的前提下,煤储层渗透率又是制约煤层气开发成败的关键因素之一[1-2]。鉴于此,国内外诸多学者针对煤储层渗透率的分析预测提出了不同的研究方法,煤储层渗透率的研究也逐渐从定性评价发展为结合神经网络、数理统计分析方法、分形理论、测井评价和三轴应力实验等先进技术的定量评价[3]。其中,数理统计分析方法已较为完善,在常规油气领域中,该方法对渗透率的分析起到了很大作用,但应用的广度和深度尚不够。近年来,在常规油气领域里,神经网络越来越多被应用到储层地质参数的预测中,并已取得了不错的效果[4-6]。煤储层与常规油气储层之间存在较大差异,用神经网络模型预测煤层渗透率的研究成果虽有报道[7],但基于测井信息的煤层渗透率神经网络文献尚未见及。本文拟在山西柳林区块3+4号煤层试井有效渗透率的基础上,结合丰富的测井信息,利用灰色关联分析法和GA-BP神经网络对该区块3+4号煤层渗透率进行预测分析,建立煤层原地渗透率预测的数学模型,实现全区煤层高渗区的半定量预测。

1 地质概况

柳林区块位于山西省西部,鄂尔多斯盆地东缘中段,南邻石楼北区块,东邻杨家坪区块,北邻三交区块;区块面积194.42 km2,煤层气资源量369.21×108m3。

柳林区块构造上位于鄂尔多斯盆地东缘石鼻状构造南翼[8-9]。在研究区北部,地层向西倾斜,向南逐渐转为向西南倾斜,总体为一向西或西南倾斜的单斜构造。地层产状平缓,倾角约3 °～8 °。在鼻状构造的背景上,发育有起伏微弱的次级小褶曲,起伏高度一般小于50 m。区内断层不发育,仅在区块北部发育有由聚财塔南北向正断层组成的地堑及其派生的小型断层。地表未见陷落柱,也未见岩浆活动。

柳林地区出露地层由老到新依次太古界、寒武系、奥陶系、石炭系、二叠系、三叠系和新近系,其中上石炭统太原组(C3t)和下二叠统山西组(P1s)为主要含煤层系(见图1),而石盒子组、本溪组仅含薄煤层或煤线,基本无开采价值。

该区以焦煤为主,可采煤层大约在10层左右,其中煤层气开发目标层位为山西组的3号、4号、5号煤层和太原组的8号、9号、10号煤层。

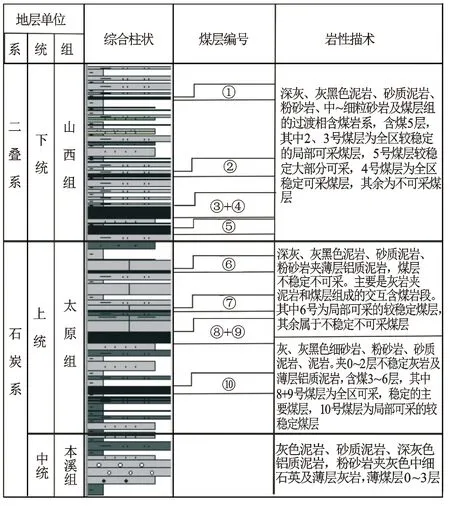
图1 柳林区块含煤地层综合柱状图

2 煤层渗透率GA-BP神经网络建模

2.1 基于遗传优化的神经网络(GA-BP)模型

BP(Back Propagation)神经网络[10]是一种按误差逆传播算法训练的多层前馈网络。BP神经网络模型拓扑结构包括输入层、隐含层和输出层。BP算法因其简单、易行、计算量小、并行性强等优点,曾是神经网络使用最多的算法之一[11]。但随应用范围逐步扩大,BP神经网络也暴露出很多缺点和不足,如训练时间长、不能保证权值为误差平面的全局最小值、网络隐含层的层数和单元数的选择尚无理论上的指导等。

为解决渗透率预测的复杂非线性问题,将BP神经网络与遗传算法(genetic algorithms,GA)[12]结合起来,用遗传算法优化网络结构和连接权值,提出一种用于预测渗透率的GA-BP方法。该方法既减小了人为选择网络结构的盲目性,又能全局优化神经网络的权值,达到预测模型收敛速度快,易于训练的目的。

遗传算法与神经网络的结合主要有2个目的:一是用于网络训练,优化网络各层间的连接权值;二是学习网络的拓扑结构,优化网络的隐含层神经元个数[13]。

2.2 煤层渗透率预测参数优选

为取消各维数据间的数量级差别,避免因为输入和输出数据数量级差别较大而造成预测误差较大,必须对数据组进行归一化处理。最常用的归一化方法是最大最小法,函数形式为

xk=(x0-xmin)/(xmax-xmin)

(1)

式中,xk为经归一化计算后的测井曲线,xk∈[0,1];x0是原始测井数据;xmax及xmin分别为该测井曲线的极大值和极小值。

多种测井手段获得的数据是多元化的,若直接用到建模中,必定引入某些噪音信息,导致所建立模型的可信度降低。有人在建模前拟对变量进行加权处理,这实际上不可取,因为这会破坏原始数据的真实统计分布特征。对于GA-BP神经网络模型而言,选择合适的输入变量尤为重要,不恰当的变量将直接导致网络收敛的局部过优(过训练)。本文采用灰色关联分析法,它是一种多因素统计分析方法,以各因素的样本数据为依据用灰色关联度描述因素间关系的强弱、大小和次序,若样本数据反映出的两因素变化的态势(方向、大小和速度等)基本一致,则它们之间的关联度较大;反之,关联度较小。该方法的优点在于思路明晰,减少由于信息不对称带来的损失,并且对数据要求较低,工作量较少。最终可计算出研究对象与待识别对象各影响因素之间的关联度,通过比较各关联度的大小判断待识别对象对研究对象的影响程度。从众多变量值中提取强影响力自变量作为GA-BP神经网络的输入端,从而减少噪音信息,提高模型可信度。

通过对全区已获得的56组数据施以灰色关联分析后发现,各测井响应对于渗透率参数具有不同的影响(见表1)。由灰色关联分析的基本原理可知,关联度大表明该影响因子对于输出变量具有较大的影响力,即具有强的全局相关性,因而对于输出变量具有较好的预测能力。GA-BP神经网络能否预测成功,很大程度上取决于变量选择是否合理。

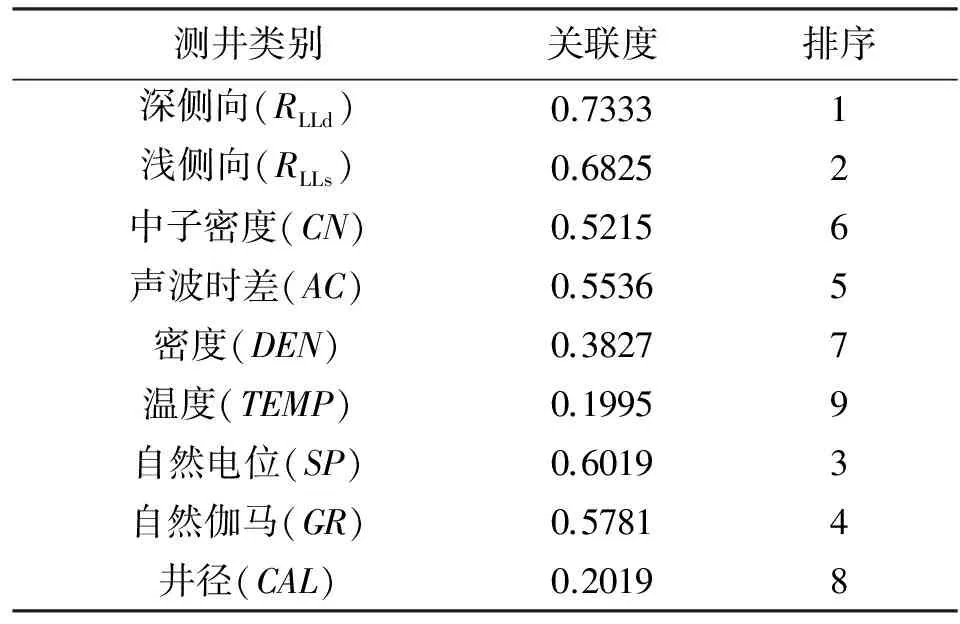
表1 灰色关联分析结果

根据表1的分析结果,选用关联度排序前6的深侧向、浅侧向、自然电位、自然伽马、声波时差、中子密度作为输入变量。

2.3 煤层渗透率的GA-BP神经网络预测

经过模糊曲线分析后,选择深侧向、浅侧向、自然电位、自然伽马、声波时差、中子密度6种曲线作为模型的输入因子,渗透率则单独作为输出变量。从56组测试数据中随机抽取30组作为训练样本,其余用来测试预测精度。为达到提高收敛速度和训练结果可靠性的目的,选择简单的3层BP神经网络(见图2)。

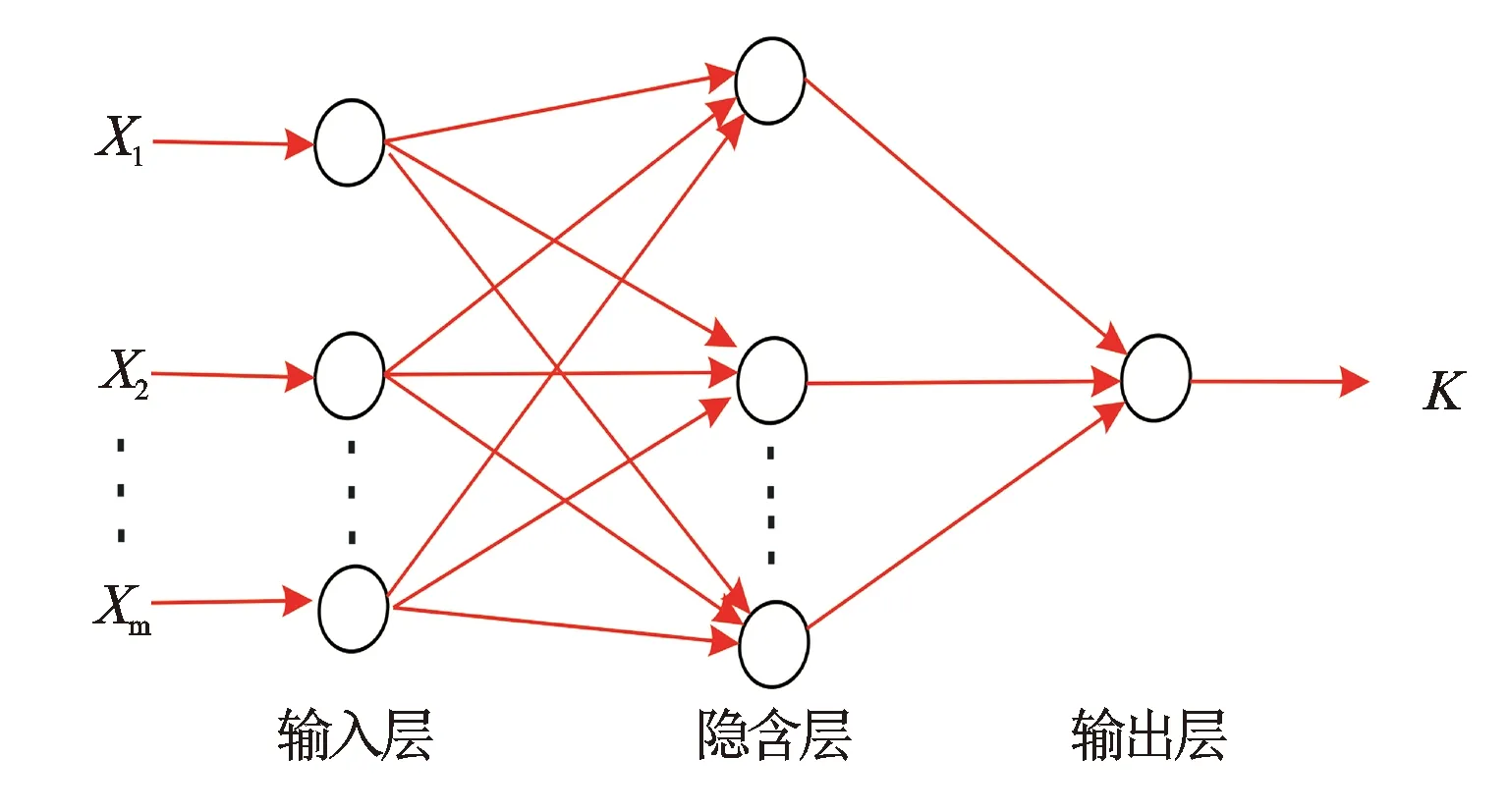
图2 预测时使用的BP神经网络结构示意图

在对30组样本经过近20 000次的训练之后,网络趋于稳定。把其余26组数据作为检验样本,在所有数据输入网络后,就可得到预测结果。再把预测的渗透率和试井渗透进行拟合,发现二者的相关性较好,复相关系数R2达到0.996 2(见图3)。

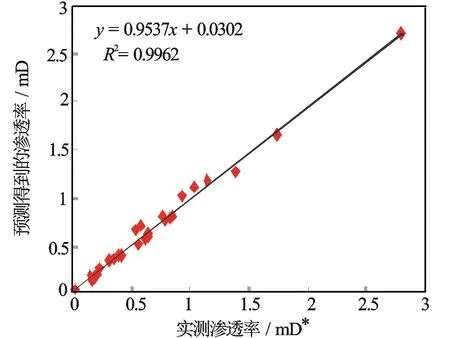
图3 GA-BP神经网络模型的预测值与实测值的拟合关系*非法定计量单位,1 mD=9.87×10-4 μm2,下同

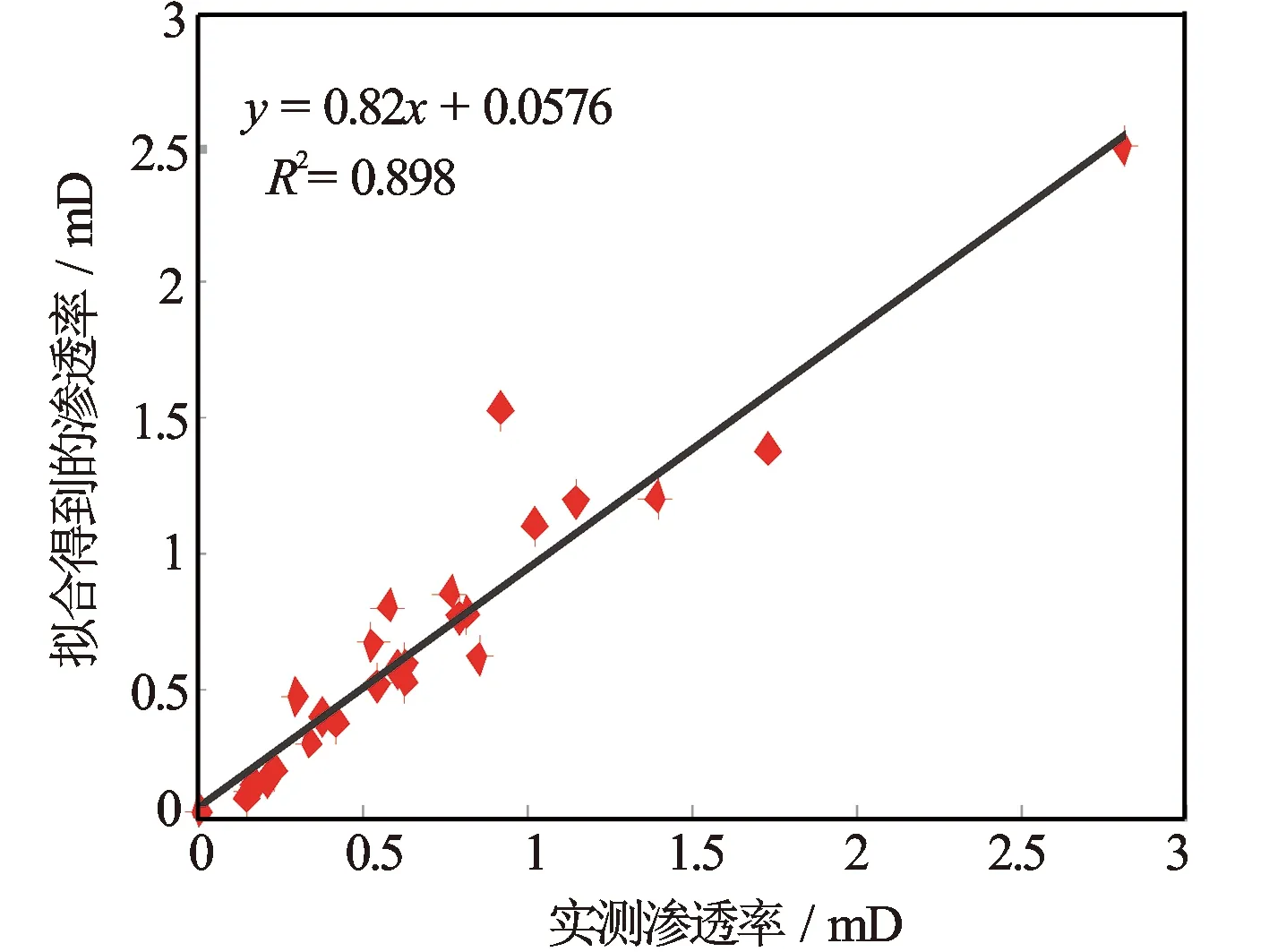
图4 逐步回归的预测值与实测值的拟合关系

为验证神经网络模型应用到预测煤储层渗透率中的合理性,用数理统计分析的方法计算该区3+4号煤层的渗透率。同样,在56组数据中随机挑选30组数据进行逐步回归分析,得到线性拟合公式

K=-0.062SP-0.009GR-0.014AC-

0.001CN-0.005RLLs+0.004RLLd+12.472

(2)

然后用该公式计算出另外26组测井数据的预测渗透率值,同样将二者进行线性拟合,其拟合结果见图4。对比图3和图4可以发现,较回归分析而言,由灰色关联和神经网络建立的渗透率预测模型具有更高的精度。

3 模型应用

山西组3号、4号煤层为柳林区块的主力煤层,多煤层发育地区常常是中国煤层气资源集中赋存区,煤层气开发前景巨大。对多煤层发育地区实施分层压裂、合层排采工艺技术是降低煤层气开发成本、提高产能的重要举措之一[14],因而山西组3号、4号煤层往往是作为合层开采的,记为3+4号。在研究过程中,一般定义参数c,称之为产气能力。

c=h×s×K

(3)

式中,h、s、K分别为煤储层的有效厚度、含气量和渗透率。可见,渗透率参数对资源评价和高产区预测有着重要的作用。然而,由于试井资料往往很有限,而经岩心测试的渗透率又不能完全反映煤层在地下的真实情况,即原位渗透率,这导致柳林地区的渗透率资料稀缺,从而使得高产区预测成为了开发中亟待解决的难题。在柳林区块的南区和北区曾开展过大量的测井解释工作,所以测井数据较充足。

前文对GA-BP神经网络用作煤储层渗透率预测的合理性进行过验证,证明这是一种简单、直观、准确的预测方法,这就为获取该区更多渗透率值提供一种行之有效的途径。据此,采用所建立的预测模型和方法获得了覆盖全区3+4号煤层渗透率,为柳林地区煤层气开发工程优化部署提供了重要依据。

4 结 论

(1) 在测井资料的基础上,用GA-BP神经网络方法预测渗透率可获得钻井剖面中连续、完整的渗透率变化和分布特征。利用煤层试井渗透率数据和测井信息对柳林区块煤储层渗透率进行预测,建立了一种适合于柳林区块地质条件的煤层渗透率GA-BP神经网络预测模型。

(2) 模型建立之前,参数优选是必不可少的一项工作,灰色关联分析法可解决此类问题。其次,要充分利用测井参数信息和基础地质资料建立全面、合理的训练样本,使预测结果更加接近客观实际。

(3) 回归分析方法在预测储层地质参数的应用由来已久,但地质参数与测井响应值之间往往不是简单的线性关系。相比之下,神经网络是一个具有高度非线性的动力学系统,它在预测复杂非线性关系时,优势明显。所以在预测模型的选择中,神经网络要优于线性回归分析的方法。

参考文献:

[1] 薄冬梅, 赵永军, 姜林. 煤储层渗透性研究方法及主要影响因素 [J]. 油气地质与采收率, 2008, 15(1): 18-21.

[2] 艾池, 粟爽, 李净然, 等. 煤岩储层渗透率动态变化模型 [J]. 特种油气藏, 2013(1): 71-73.

[3] 王相业, 李建武, 杨志远, 等. 柳林地区煤层渗透率逐步回归分析与预测 [J]. 煤田地质与勘探, 2013, 41(3): 18-22.

[4] 娄建立, 谭世君. 神经网络技术用于测井解释的评述 [J]. 测井技术, 1999, 23(5): 389-392.

[5] 李勇, 刘宗林. 利用测井与地球化学信息判断储层水淹程度 [J]. 油气地质与采收率, 2002, 9(3): 40-42.

[6] 李凤杰, 王多云, 苑克增, 等. 人工神经网络技术在油田储层物性预测中的应用——以西峰油田为例 [J]. 天然气地球科学, 2004, 15(3): 243-246.

[7] 尹光志, 李铭辉, 李文璞, 等. 基于改进BP神经网络的煤体瓦斯渗透率预测模型 [J]. 煤炭学报, 2013, 38(7): 1179-1184.

[8] 袁鼎, 单业化. 山西柳林鼻状构造曲率特征及其与煤层气的关系 [J]. 中国煤田地质, 1999, 11(2): 28-31.

[9] Yuan D S, Shan Y H. CurvatureFeatures of Liulin Nose Structure of Shanxi Province and the Relationship with Coal Bed Gas [J]. Coal Geology of China, 1999, 11(2): 28-31.

[10] 李晶, 栾爽, 尤明慧. 人工神经网络原理简介 [J]. 现代教育科学, 2010, 24(1): 45-50.

[11] 吴建生, 金龙, 农吉夫. 遗传算法BP神经网络的预报研究和应用 [J]. 数学的实践与认识, 2005, 35(1): 83-88.

[12] 刘春艳, 凌建春, 寇林元, 等. GA-BP神经网络与BP神经网络性能比较 [J]. 中国卫生统计, 2013(2): 173-176.

[13] 李大卫, 王梦光. 一种改进的混合遗传算法 [J]. 信息与控制, 1997, 26(6): 449-454.

[14] 邵长金, 邢立坤, 李相方, 等. 煤层气藏多层合采的影响因素分析 [J]. 中国煤层气, 2012(3): 8-12.