城市建筑物出口与道路连接处通行能力研究

熊文华 林 思

（1.广州市交通规划研究院 广州510030；2.佛山市交通运行监测中心 广东 佛山528011）

0 引 言

交通影响评估工作是提高城市土地开发利用科学性和合理性的重要手段之一。近年来，国内城市已越来越重视交通影响评估工作，尤其像广州等大城市已将此工作纳入城市规划管理的主要环节。但如何确定城市道路两侧的建筑物出口与道路连接处的通行能力，历来是交通影响评估研究的难点所在。国外的相关研究中，以美国的研究工作最具代表性。从文献［1-4］可以看出，美国主要是利用出入口管理手册（access management manual，AM）对大型公共建筑机动车出入口交通问题进行研究，其研究对象为各级道路的出入口。但美国主要是通过对开发地块通道和交叉口的有效治理来保证道路出入口交通的安全与顺畅，对建筑物出入口到底能够有多少车流可以插入到主路的研究并不多。在国内的研究中，主要还是集中在道路路段和道路交叉口的通行能力研究等方面，如文献［6］提出了系统的道路通行能力理论，文献［7-8］对信号交叉口的插入间隙模型进行了研究，文献［9-11］主要是对非信号交叉口通行能力等有所研究。上述研究对道路和交叉口的，但建筑物出口对道路交通的影响主要在于车辆通过道路车流间的交通流特性进行了研究，对本次研究具有一定参考意义。

但建筑物出入口车流从出口汇入到道路的过程中，汇入车辆会对道路的上游车流造成干扰，从而降低上游车流通过能力；而车辆在汇入道路后，也会增加道路外侧车道的流量，伴随着道路车流量的增加，道路车流速度和道路饱和度也随着变化，从而影响道路车流的通行。由于一直以来都忽视了对这一问题的研究，导致在进行城市道路交通影响评估时，总是难于获得理想的效果。因此，近年来国内交通界开始针对建筑物出入口进行研究，其中文献［5］通过分析机动车出入口的车头时距，利用排队论的方法建立了出入口通行能力和服务水平的模型，但该研究成果主要是为解决出入口设置的问题，并未回答“建筑物出入口处能够插入多少车流”这个问题。

实际上，从几何特征来看，建筑物出口与道路之间组成一个“T”形的交叉口形式，这与主路优先的无信号“T”形交叉口的图谱结构具有一较高的相似性。因此，本次研究主要是参照主路优先的无信号交叉口次要道路车流插入的可接受间隙理论模。但是目前的可接受插入间隙理论模型主要是针对城市道路主次干道相交路口进行的理论研究，与城市道路两侧的建筑物出口与道路连接处的通行能力研究还存在一定的差异性。因此本文在参照主路优先的无信号交叉口次要道路的车流插入间隙理论模型基础上，通过实际调查数据对模型参数进行修正和标定，获得了城市建筑物出口与道路连接处的通行能力模型，较好地解决交通影响评估存在的难于合理确定城市土地利用开发对道路交通影响的难题。

1 可接受间隙理论模型及其局限性分析

可接受间隙理论模型主要是针对主要道路与次要道路组成的交叉口。模型假设主路车流优先通过交叉口，即通过交叉口时不受影响，不产生延误，而从离开的车辆（次路车流）必须在交叉口前等待，只有当主路车流出现足够大的间隔，次要道路的车辆才能利用主路车流的间隙通过。在该假设下，若已知主路车流的流率及车流中车头间隙的分布规律，则能求出次要道路在一定时段内经间隙插入主路车流的车辆数［4－5］。

根据上述假设可得到

式中：Q为主路车流的流量；Qm为次路车流的流量；tc为主路车流可插入临界间隙；tf为次路车流跟随时间，一般情况下tc＝6～8s，tf＝3～5s。

由可接受间隙理论前提假设可知，该模型应用于建筑物出口可插入车流能力计算时，还存在以下局限性。

1）主路可接受间隙tc和次要道路车辆跟随间隙tf是固定值，不能体现不同等级道路对建筑物的可插入流量的容忍差异。

2）模型假设次要道路可容纳无穷多辆车排队，即n可以为无穷大，而实际上，建筑物出口前因空间有限，可容纳排队车辆数为有限值。

2 模型的修正及参数标定

根据对现有模型的分析可知，建筑物出口前因空间有限，可容纳排队车辆数n为有限值，同时Q，tc等2个参数会受主路车流速度的影响而变化。因此笔者主要研究建筑出口可容纳排队车辆数n、主路车流速度对模型的影响，并加以修正。

2.1 建筑物出口可容纳排队车辆数对模型的影响分析

假设建筑物出口最多可容纳n辆车排队，则为当主路车流间隙为t时，有k辆建筑物的车辆进入主路 （k≤n），其概率pk（t）有

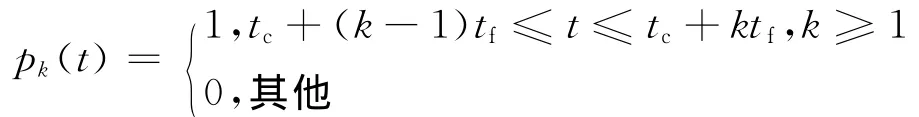
则建筑物的车辆利用间隙t进入主路的车辆数为：

由于建筑物出口可以容纳n辆车排队，因此当t＞tc＋ntf时，次路进入主路车辆达到最大数n，车辆数并不会随着主路的间隙t的增大而增加。故原推导公式（t）·g（t）dt应分为2个阶段，即当tc＋（n－1）tf≤t≤tc＋ntf时，有Qm＝f（t）·g（t）dt，当t＞tc＋ntf时，有Qm＝f（t）dt，因此建筑物出口车流Qm应为

由上式可知，建筑物出口可容纳排队车辆数对原模型的影响系数a为 （1－e－nQtf），该系数的取值范围小于或等于1，说明建筑物出口的可容纳排队车辆数对原模型具有折减作用，下图是a随着n增大的变化情况（假设Q＝600pcu，tf＝3s）。

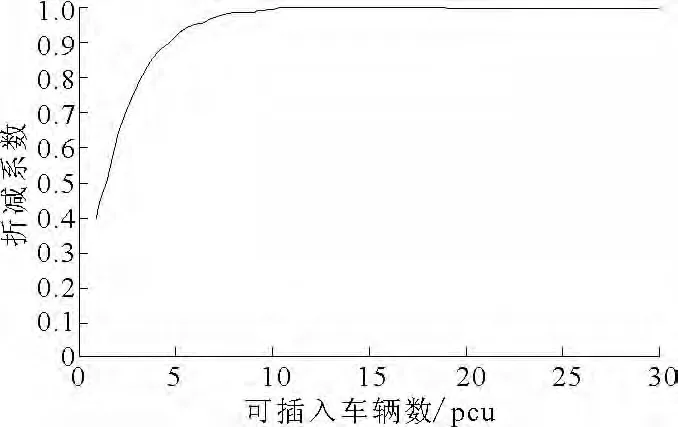
图1 折减系数a随可容纳车辆数n的变化情况Fig.1 The relationship between reduction factor a and accommodate vehicle number n

2.2 主路车流速度对主路可接受间隙tc的影响分析

根据既有理论可知，主路的临界间隙（tc）是指在主路车流中出现的驾驶人能接受的最小间隙，一般情况下，驾驶人会拒绝1个小于临界间隙的时间间隔而接受1个大于临界间隙的时间间隔。实际上，驾驶人可接受的临界间隙不是1个常量，它的分布函数及其参数值不能直接测量获得，目前大多数的应用多取其经验值（大型车取10～8s，混合车取8～6s，小型车取6s）。

假设建筑物出口是右转进入主路，初始速度为v0，主路车流速度为v，车身长度为L0，主路车流行驶时最小安全间距为h（前车后悬与后车前悬之间的距离），建筑物出口车辆可汇入主路时主路车流的间距为L（前车后悬与后车前悬之间的距离），次路车辆汇入主路所用时间为t。

在次路车辆汇入主路过程中，次路车辆从速度v0加速到速度v，其在主路行驶的距离为：S1

此过程中，主路前车和后车行驶的距离为：S2＝v·t

为了使建筑物出口车辆汇入主路过程中不影响主路车辆行驶，应该满足插入车辆与前车和后车均要保持安全距离，即：前车与插入车之间间距（前车后悬与后车前悬之间的距离）L1＝S2－S1

插入车与后车之间间距（前车后悬与后车前悬之间的距离）

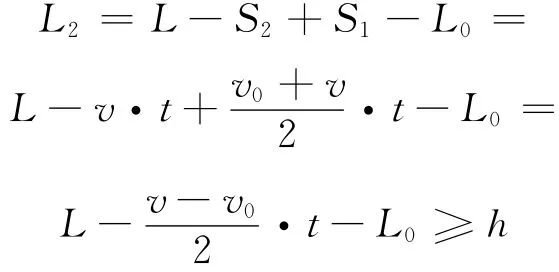
得出：L≥L0＋h＋

于是得出主路车流可插入临界间距L与主路车流速度v、次路车辆速度v0之间的关系，Lmin

若把次路车辆在插车过程中，看作是匀加速运动，汽车加速度为a，根据物理学定义，汽车在加速过程中有

v＝v0＋a·t得，代入上式，可得

（1）参数标定。车辆长度L0。汽车长度跟汽车车型设计有关，参考规定中的机动车尺寸如下。

表1 不同车型车长参考值Tab.1 The vehicle length reference value of different types

（2）安全间距h。是指车辆在行驶过程中后车车头与前车车尾间距离，是保证前后2车不发生追尾事故的重要参数，一般而言，前车发生制动操作后，后车驾驶人在开始制动前需要0.7s的反应时间（驾驶人反应时间与制动器反应时间），因此安全间距是保证在此反应时间内，后车不会追上前车的距离。表2是在不同速度下的安全间距要求。

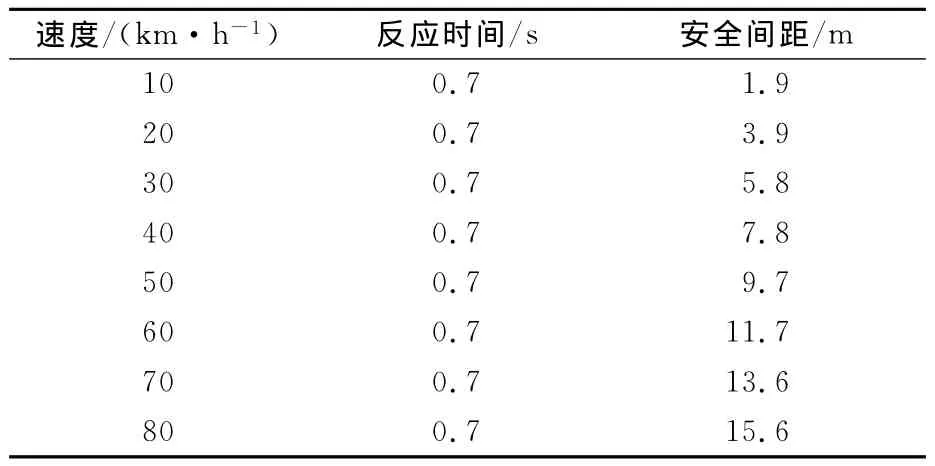
表2 不同速度下车辆制动反应纵向安全间距情况Tab.2 The reaction safe distance with different speeds

（3）加速度a。本次定义的加速度是汽车在操作过程中的平均加速度，其大小不仅与汽车性能有关，还与在操作过程中驾驶人的操作熟练程度有关，通过在不同路段的右转车辆汇入主路加速时间的调查，可以统计得出车辆在不同情况下的平均加速度，本次研究建议加速度a的取值为2.5～3.5m／s2。

表3 不同速度下车辆右转汇入主路时间统计情况Tab.3 The time of turn right into the main road with different speeds

2）主路车流可插入临界间距L的回归分析。通过多次调查记录主路上每个间距的大小L和在该间距中插入的车辆数，再以每辆车的可插入平均间距进行线性回归，得出可插入临界间距L的观测值，与公式推导的计算值（取小客车L0＝5 m，a＝3m／s2）进行对比分析，见表4。

调查发现，主路的可插入临界间距随着主路速度的增加而增加，通过回归分析，主路不同速度的情况下，主路可插入临界间距的观测值与推导公式计算值之间的偏差范围在10%以内，属于可接受偏差范围，可见模型公式的建立是可接受的。

3）可接受的临界间隙（tc）的修正。根据定义，主路可接受间隙tc是主路车流中2辆车的车头时距，即

由以上函数关系式可知，主路车流可接受临界间隙tc与主路车流速度（v）、次路车辆起始速度（v0）、车型（L0）和插车过程的操作（a）等因素有关。主路车流速度越大，需要的可接受临界间隙越大；车型越大，可接受临界间隙越大；插车过程操作越困难，需要的可接受临界间隙越大；低速插入比停车插入通过的可接受临界间隙小。

式中，对于停车待机通过者，若取v0＝0，a＝3m／s2，小汽车L0＝5m，则

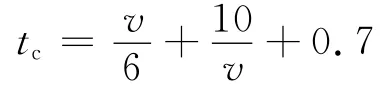
2.3 主路车流速度与主路流量的关系对模型的影响分析

车流速度v、道路交通量流Q和交通流密度是交通流理论三大参数，车流速度与交通流量之间有着内在的联系，同一道路的不同流量，车流速度也不一样，两者关系可以用v＝v（Q）来表示。从定性上分析，车流在稳定流范围内，Q越大，速度v越小。本次研究通过参照广州模型采用的速度流量函数关系，归纳得出v与Q的定量关系式，各路段类型流量速度关系见表5。

另一方面，随着建筑物的车流插入到主路，主路车流下游的流量将增加，伴随着主路车流速度将会降低，从而进一步影响建筑物插入的车辆数，主路车流与建筑物出口可插入车流量相互制约的过程是1个动态的过程。

表5 各路段类型的速度流量函数关系Tab.5 The V-C function relationship of different road grade

3 不同等级道路建筑物出口可插入车流能力模型

综合以上各种情况分析可知，不同等级道路情况下建筑物出口可插入车流量是不同的，此数值与建筑物出口的可容纳排队车辆数有关，更与主要道路的车流速度有关，主路车流速度又与主路流量息息相关，会随着主路车流量的变化而变化，综合考虑以上各因影响因素，得出不同等级道路条件下，建筑物出口可插入车流量的计算过程如下。

第1步。根据主路的车流状况Q，结合道路等级，根据表5中函数关系计算出主路车流速度。

第3步。根据公式Qm＝Q·（1－e－nQtf），计算出建筑物出口可插入车流量Qm1。

第4步。令Q＝Q＋Qm1，计算出建筑物出口可插入车流量初始值后，根据主路最新的流量情况，重复前3步操作，计算Qm2。

第5步。重复迭代计算，当前1次计算的Qm（n－1）与后 1 次计算的 Qm（n）相 等，即 Qm（n）＝Qm（n－1）或Qm（n）＝Qm（n－2）时，停止计算，次要道路最终的建筑物出口可插入车流量Qm＝Qm（n）。

根据以上的计算过程，计算不同道路等级道路条件下建筑物出口可插入车流量，得出建筑物出口可插入车流量随道路等级变化关系图，见图2。

图2 建筑物出口可插入车流量与道路等级关系图Fig.1 The relationship between insertable traffic volume in entrance of buildings with road grad

4 结束语

为提高城市规划的科学性和合理性，国内外一些大城市都研究建立了基于城市土地利用开发的交通影响评估机制。笔者针对交通影响评估工作存在的难于准确确定城市道路两侧的建筑物出口的可插入车流量这一难点问题进行研究。本次研究目的主要是基于交通调查和广州交通模型的成果而进行的。本次研究通过分析建筑出口可容纳排队车辆数及主路车流速度对建筑物出口可插入车流能力的影响，对既有可接受插入间隙理论模型的参数进行修正和标定，得出了不同等级道路两侧建筑物出入可插入车流量的计算模型。通过对建筑物出入口交通特征的观察，本次研究建立的模型对实际运行状具有更好的拟和性，比较接近实际交通运作特征，由此可见研究成果基本可以验证该方法在技术上是基本可行的。目前该成果已在广州市交通影响评估工作得到实际运用。但由于很多应用项目尚处于规划或建设阶段，短期内难以项目难以建成或达到正常运营的阶段，因此，建筑物出入口开通前后的实测数据难以获取，因此模型的精度等还需要今后进一步采集数据后验证。同时，建筑物出口内路侧视距、公交汽车站、混合交通等均对建筑物出口与道路连接处的通行能力产生一定程度的影响，也需要在下一步将通过收集更多实际交通数据，进一步细化和校正模型的相关参数，以提高模型的准确性和实用性。

［1］ Transportation Research Board of the National A-cademies.Highway capacity manual［M］.Washington.DC，Transportation Research Board，2010.

［2］ Aty Mohamed A，Roundabouts design，modeling and simulation［R］.Florida：Department of Civil and En-vironmental Engineering.University of Central Florida，2001.

［3］ Rouphail N，Tarko A，Jing L.Traffic flow theory.Part 9：Traffic Flow at Signalized Intersections［M］.Federal：Federal Highway Administration，2011.

［4］ Hagring O.Derivation of a capacity equation for a roundabout entry with mixed circulating and exiting flow［R］Washington.DC：Transportation Research Board，2001：91-99.

［5］ 钟 园.建设项目出入口通行能力研究［D］.北京：北京工业大学，2010.ZHONG Yuan.Study on the capacity of constructive project access［D］.Beijing：Beijing University of Technology，2010.（in Chinese）.

［6］ 张亚平.道路通行能力理论［M］.哈尔滨：哈尔滨工业大学出版社，2007.ZHANG Yaping.Theory of road capacity［M］.Harbin：Harbin Institute of Technology，2007.（in Chinese）.

［7］ 郭瑞军.基于间隙接受理论的环形交叉口通行能力研究［D］.北京：北京交通大学，2013.GUO Ruijun.Study on capacity of roundabouts based on gap acceptance theory［D］.Beijing：Beijing Jiaotong University，2013.（in Chinese）.

［8］ 郑 柯，张起森.无信号交叉口可接受间隙理论模型修正分析 ［J］.长沙交通学院学报，2001，17（1）：125-129.ZHENG Ke，ZHANG Qisen.Analysis of amending gap acceptance theory′s model at un-signalized intersections［J］.Journal of Changsha Communications University Natural Sciences，2001，17（1）：125-129.（in Chinese）.

［9］ 张兰芳，方守恩.公路平面交叉口合理间距研究［J］.重庆交通大学学报，2008，27（2）：276-278.ZHANG Lanfang，FANG Shouen.Study on the reasonable spacing of highway intersections［J］.Journal of Chongqing Jiaotong University Natural Sciences，2008，27（2）：276-278.（in Chinese）.

［10］ 曹晓奎，裴玉龙，李 龙，等.停车场出入口布置相关问题研究 ［J］.城市交通，2010，8（2）：61-65.CAO Xiaokui，PEI Yulong，LI Long，et al.A study on parking entrance／exit layout design ［J］.Urban Transport of China，2010，8 （2）：61-65.（in Chinese）.

［11］ 马 琳.快速路公交站设置对出入口通行能力影响的研究［D］.北京：北京交通大学，2010.MA Lin.Impact analysis of public stops layout on capacity of exit and entrance of urban expressway［D］.Beijing：Beijing Jiaotong University，2010.（in Chinese）.