利用速度信息改进城市道路短时交通量预测

张润民 夏井新 黄 卫

（东南大学智能运输系统研究中心 南京210096）

0 引 言

短时交通流预测是智能交通系统的重要组成部分，它是实现城市道路交通先进控制与诱导的基础和关键，因此与其相关的理论和应用研究已成为交通领域的研究重点和热点之一。在过去的几十年里，研究者们做了大量的工作并提出了各种的短时交通流预测模型，它们大致可以分为7类：基于统计方法的模型、动态交通分配模型、交通仿真模型、非参数回归模型、神经网络模型、基于混沌理论的模型、综合模型等［1，2］。在众多的短时交通量预测模型中，基于统计理论中最优估计的卡尔曼滤波模型由于具有预测因子选择灵活、模型参数少、计算效率高、在线预测能力强等特点，在交通流量预测领域中得到了广泛应用。

卡尔曼滤波是Kalman［3］于1960年提出的1种最优状态估计方法，可以应用于受随机干扰的动态系统。该算法由一系列递归数学公式组成，它们提供了1种高效可计算的方法来估计过程的状态，并使估计均方误差最小。卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质［4］。Okutani等［5］最先将卡尔曼滤波算法应用于交通流量预测并取得了令人满意的计算结果，Whittaker等［6］将卡尔曼滤波算法应用于城际公路的交通量预测，杨兆升等［7］提出了基于卡尔曼滤波理论的交通流实时预测模型，Yue［8］对在相邻位置观察到的交通流进行时空关系分析，建立了时空卡尔曼滤波模型。此外，还陆续发展出各种基于卡尔曼滤波算法的混合预测模型和组合测模型［9–15］。

现有基于卡尔曼滤波的交通量预测模型中，状态变量会被假设为平稳的，并采用单位矩阵作为状态转移矩阵；然而城市交通流一般具有明显的动态性，因此采用时变矩阵作为状态转移矩阵，将更能符合实际情况。另一方面，现有模型通常只采用交通流量信息作为输入数据，没有包括其他的交通状态变量；但随着科技的不断进步，安装在道路上的检测设备除了能够获取交通流量信息外，还可以同时得到诸如速度、占有率、车头时距等其他的交通相关信息，而根据交通流理论可知，速度是与交通流量密切相关的，因此若能充分利用已知的速度信息，则有望进一步提高预测的准确度。

1 利用速度信息改进预测模型

1.1 基于卡尔曼滤波的短时交通量预测模型

利用卡尔曼滤波算法进行交通流量预测时，一般假设某路段l在τ＋k时段的交通量z（τ＋k）是各上游路段ei（i＝1，2，…，m）在τ时段及之前r个时段的交通量f（τ），f（τ－1），…，f（τ－r）的线性函数

式中：Hj（τ）（j＝0，1，…，r）为参数矩阵；f（τ）＝ ［f1（τ），f2（τ），…，fn（τ）］T为各上游路段交通量组成的向量，w（τ）为误差项。设

则式（1）可改写为以下形式

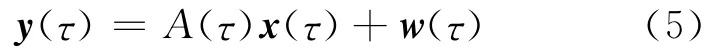
同时令

式中：B（τ；τ－1）为参数矩阵；u（τ－1）为误差项。经上述变换后，以式 （5）作为观测方程，式（6）作为状态方程，便可得到1个状态空间模型，继而可以利用如下的卡尔曼滤波算法递推方程组，对状态变量x（τ）的估计值＾x（τ）进行求解

式中：K（τ）为卡尔曼增益矩阵；P（τ｜τ－1）和P（τ）分别为＾x（τ｜τ－1）和＾x（τ）的估计误差协方差矩阵；Q（τ）为系统过程噪声w（τ）的协方差矩阵；R（τ）为观测噪声u（τ）的协方差矩阵，均为对称非负定矩阵。

1.2 模型的改进

在基于卡尔曼滤波的短时交量预测模型中，通常会假设状态变量x（τ）是平穏的，因而状态转移矩阵B（τ；τ－1）可取单位矩阵I，使得式（6）简化为

上述的状态变量x（τ）是由式（1）中的系数矩阵Hi（τ）所组成，通过分析交通流运作机理可知，Hi（τ）的取值主要会受到2方面的因素影响：①上游车辆的路径选择；②车辆的行程时间。由于车辆的行程时间是随着路面的交通状况而变化的，具有一定的时变特性，若状态转移矩阵B（τ；τ－1）的取值选为时间变量τ的函数而非固定值，令x（τ）具有适当的动态性，会更符合实际情况。

假设车辆从上游路段ei的检测断面到达目标路段l的检测断面所经历的行程时间为ξei，l，则ξei，l与该行程上的行驶速度vei，l的倒数有关，因此vei，l应该是影响状态变量x（τ）的因素之一；另一方面，根据交通流理论，速度是描述交流状态的主要指标之一，因此在式（6）中的状态转移矩阵B（τ；τ－1）应与速度信息有关。然而，vei，l随时间和位置变化，要准确获得其数值将需要采用复杂的检测技术并且费用高昂，因而在实际操作上往往并不可行。尝试利用可获取的断面平均车速来对其进行近似估计。将路段l及其上游路段ei在τ时段内所检测到的车辆平均速度（τ）及（τ）的算术平均值（τ）＋（τ））／2作为整个行程的平均速度i的近似值，亦即以起点及终点的速度来估算整个行程的平均速度，则行程时间ξei，l与2／（τ）＋（τ））相关。然而，两者之间的具体函数关系尚未能决定，因此一般可假设ξei，l与2／（τ）＋（τ））的n次方相关。其中：n为待定系数。显然，除了n＝0和n＝1的情况外，都将会出现非线性关系。考虑到所采用的卡尔曼滤波模型属于线性模型，为避免引入非线性项，因此对上述变量之间的相关性进行对数变换，由于［2／（（τ）＋（τ））］n取 对 数 后 转 化 为n×［ln（2）－ln（τ）＋（τ））］，因此不管n的实际值是多少，该表达式均保持为线性的。

按照以上的分析，则式（6）中的状态转移矩阵B（τ；τ－1）采用由（r＋1）×m 个元素bj，i（τ；τ－1），（j＝0，1，2，…，r；i＝1，2，…，m）组成的对角阵组成的对角阵，具体形式如下

其中的对角元素bj，i（t；s）按如下方式取值

由于待定系数n同时出现在分子和分母，因而相互抵消掉，所以无需对其进行求值。而按照式（13）及式（14）定义的B（t；s）能满足以下要求［16］

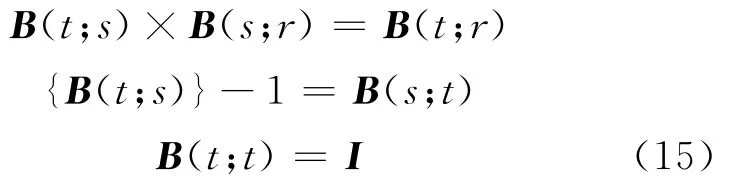
此外，当各路段上的速度保持稳定不变时，对角元素bj，i（t；s）的值将全部等于1，状态矩阵B（t；s）将退化为单位矩阵，假设x（τ）为平穏时所得的模型一致。

2 模型性能评估

为检验由式（5）、（6）、（13）及（14）所组成的改进模型的预测效果，本文利用由微波车辆检测器采集的昆山市城市道路断面交通流量和车辆平均速度数据来进行预测试验。选取了前进西路由东往西方向以及长江中路由南往北方向各1个路段（以下分别称为路段1及路段2）作为研究对象，前者属于城市主干道，而后者则属于省道。数据采集日期为2012年9月24～27日，采集时间为全天24h，采样间隔为15min。利用2种模型进行交通量预测对比分析，并假设目标路段的交通量与上游路段交通量的关系对应于式（1）中k＝r＝1的情况，原模型采用单位矩阵作为状况转移矩阵，而改进模型则按式（13）及（14）确定状况转移矩阵。预测结果如图1、图2所示。

为了能够评价和比较预测试验的结果，将使用如下几个性能指标进行分析

平均相对误差

平均绝对相对误差

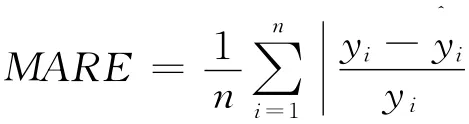
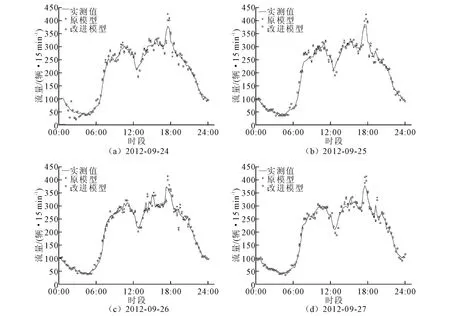
图1 路段1的预测结果Fig.1 Forecasting results of road segment I

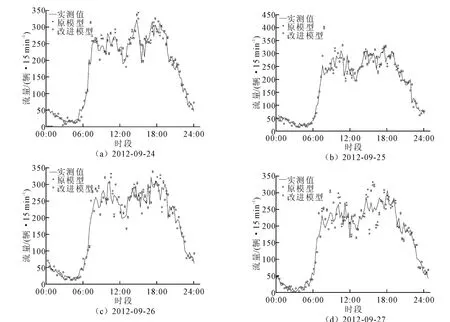
图2 路段2的预测结果Fig.2 Forecasting results of road segment II

最大绝对相对误差

相对误差平方和均值平方根

均等系数

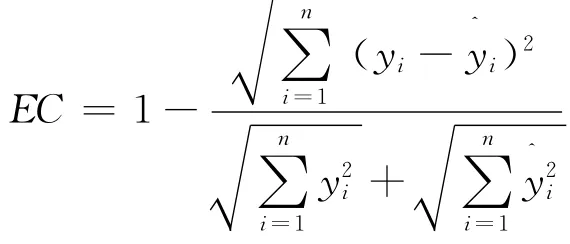
上述各式中，n为样本数；yi为实际观测值；＾yi为预测值。均等系数EC反应了预测值与实际值的拟合度，一般在0.9上为比较好的拟合；而其余各项误差指标的数值越小，预测效果越好，反之预测效果越差。2种模型的预测结果（从第20项开始计算）比较如表1所示，改进模型的预测结果在各项误差指标上均优于原模型，说明了在状态转移矩阵中引入速度信息能有助进一步提高模型的预测精度。而对于交通量急速变化的时段，提高的幅度更为明显。例如路段一在每天17：00～19：00时的时段，原模型的平均絶对相对误差（MARE）为0.084 5，而改进模型则为0.072 0，降低了14.8%。这是由于交通量的急速变化将会导致路段的平均速度明显改变，改进模型具有反映速度变化的状态转移矩阵，所以能作出更准确的预测；但当路段的平均速度变化幅度不大时，改进模型的状态转移矩阵将近似于单位矩阵，亦即与原模型非常相似，此时两者的预测结果十分接近。

表1 交通量预测结果比较Tab.1 Comparison of traffic volume forecasting results%

3 结束语

笔者在分析城市道路交通流时空关系的基础上，根据流量与速度的相关性，采用与速度信息相关的时变矩阵作为卡尔曼滤波预测模型中的状态转移矩阵，从而建立了1种改进的短时交通流量预测模型。该模型放松了对状态变量的平稳性要求，并充分利用了现代交通检测设备所采集到的各类信息，能更好地反映交通流的时变特性。其算法简单、易于编程实现，亦能满足实时应用的要求。今后可以进一步研究把占有率和车头时距等其他参数加入到状态方程中，从而能更全面地捕捉交通流的动态性，以期得到更能适应各种交通环境的预测模型。

［1］ 王 进，史其信.短时交通流预测模型综述［J］.中国公共安全：学术版，2005，1（1）：92-98.WANG Jin，SHI Qixin.The summery of the shortterm traffic flow predicts model［J］.China Public Security：Academy Volume Edition，2005，1（1）：92-98.（in Chinese）

［2］ 贾显超，陈旭梅，弓晋丽，等.基于混沌理论的短期交通流量多步预测［J］.交通信息与安全，2013，31（6）：27-32.JIA Xianchao，CHEN Xumei，GONG Jinli，et al.Multi-step short-term traffic flow prediction based on chaotic theory［J］.Journal of Transport information and Safety，2013，31（6）：27-32.（in Chinese）

［3］ KALMAN R E.A New approach to linear filtering and prediction problems［J］.ASME Journal of Basic Engineering，1960，82（Series D）：35-45.

［4］ WELCH G，BISHOP G.An introduction to the Kalman filter［R］.Chapel Hill，NC，USA：University of North Carolina at Chapel Hill，1995.

［5］ OKUTANI I，STEPHANEDES Y J.Dynamic prediction of traffic volume through Kalman filtering theory［J］.Transportation Research Part B：Methodological，1984，18（1）：1-11.

［6］ WHITTAKER J，GARSIDE S，LINDVELD K.Tracking and predicting a network traffic process［J］.International Journal of Forecasting，1997（13）：51-61.

［7］ 杨兆升，朱 中.基于卡尔曼滤波理论的交通流量实时预测模型［J］.中国公路学报，1999，12（3）：63-67.YANG Zhaosheng，ZHU Zhong.A real-time traffic volume prediction model based on the Kalman filtering theory［J］.China Journal of Highway and Transport，1999，12（3）：63-67.（in Chinese）

［8］ YUE Y.Spatial-temporal dependency of traffic flow and its implications for short-term traffic forecasting［D］.Hong Kong：University of Hong Kong，2005.

［9］ XIE Y，ZHANG Y，YE Z.Short-term traffic volume forecasting using Kalman filter with discrete wavelet decomposition［J］.Computer-Aided Civil and Infrastructure Engineering，2007，22（5）：326-334.

［10］ WU W，LIU H D，ZHOU W G.KF-MA model for short-term traffic flow prediction based on SCATS data［J］.Applied Mechanics and Materials，2010，44-47：3418-3422.

［11］ 沈国江，王啸虎，孔祥杰.短时交通流量智能组合预测模型及应用［J］.系统工程理论与实践，2011，31（3）：561-568.SHEN Guojiang，WANG Xiaohu，KONG Xiangjie.Short-term traffic volume intelligent hybrid forecasting model and its application［J］.Systems Engineering-Theory ＆ Practice，2011，31（3）：561-568.（in Chinese）

［12］ ZHANG L，SUN Y，MA J.An adaptive kalman filter for short-term traffic flow forecasting［C］.Third International Conference on Tansportation Engineering（ICTE），Chengdu，China：Southwest Jiaotong University，2011：97-102.

［13］ 聂佩林，余 志，何兆成.基于约束卡尔曼滤波的短时交通流量组合预测模型［J］.交通运输工程学报，2008，8（5）：86-90.NIE Peilin，YU Zhi，HE Zhaocheng.Constrained Kalman filter combined predictor for short-term traffic flow［J］.Journal of Traffic and Transportation Engineering，2008，8（5）：86-90.（in Chinese）

［14］ 朱征宇，刘 琳，崔 明.一种结合SVM 与卡尔曼滤波的短时交通流预测模型［J］.计算机科学，2013，40（10）：248-251，278.ZHU Zhengyu，LIU Lin，CUI Ming.Short term traffic flow forecasting model combining SVM and kalman filtering［J］.Computer Science，2013，40（10）：248-251，278.（in Chinese）

［15］ 郭海锋，方良君，俞 立.基于模糊卡尔曼滤波的短时交通流量预测方法［J］.浙江工业大学学报，2013，41（2）：218-221.GUO Haifeng，FANG Liangjun，YU Li.A short term traffic flow prediction model based on fuzzy Kalman filtering［J］.Journal of Zhejiang University of Technology，2013，41（2）：218-221.（in Chinese）

［16］ CHUI C，CHEN G.Kalman filtering with real-time applications［M］.4thEdition.Berlin：Springer-Verlag，2009.