基于灰色理论的矿井涌水量预测

叶永芳，陈 娟

（江西省煤田地质局224地质队，江西 分宜336600）

矿井涌水量是确定矿床水文地质条件复杂程度的重要指标之一，而矿井涌水事故会给煤矿生产带来巨大的财产及安全危害。矿井涌水量预测准确度的影响因素很多，如地质、开采状况、气象等。而传统的预测方法，如水文地质比拟法、水均衡法、解析法等多适用于水文地质条件简单的矿井，考虑因素较为单一，且难以对涌水量进行动态预测。在对顾桥矿南二采区水文地质条件充分认识的基础上利用灰色理论建立GM（1，1）模型对其－796m水平2013年矿井涌水量进行定量动态预测，较科学、客观地预测未来年份或月份的矿井涌水量的取值范围。

1 研究区水文地质概况

顾桥南二采区主要含水层由新生界松散砂层孔隙水、二叠系砂岩裂隙水和石灰岩岩溶裂隙水组成。各含水层之间均有有效隔水层和相对隔水层间隔。煤系中各层位的砂岩裂隙含水层，一般情况下与采区矿坑涌水没有直接关系，只有13－1、11－2、8～6－2煤层顶底板砂岩与矿坑充水有关，是煤层开采的直接充水含水层。

太原组灰岩岩溶裂隙含水层是淮南矿区的重要含水层，直接赋存在二叠系底部1煤下，是1煤层底板突水的水源。采区内煤层埋深大，在本区1煤非主采煤层，并与8、6－2煤层距离较远，对矿坑充水没有直接影响。煤系砂岩分布在煤层、泥岩和粉砂岩之间，砂层厚度小，分布不稳定，又有煤层和泥质岩石相隔，断层带一般含水性极弱，导水性差，因此砂岩之间一般无水力联系。开采浅部煤层时，新生界第四含水层（组）地下水通过基岩风化带垂直渗入补给。6－1～17－1煤远距太原组灰岩，4煤层与太原组灰岩之间有一定厚度隔水层（组）存在，天然状态下无水力联系。

区域内，在古地形隆起带，太原组灰岩接受新生界下部四含水渗入补给。从区域范围看，奥灰水也可因断层或其它因素导致其直接与太灰含水组发生水力联系，奥灰水补给太灰含水组，补给水源丰富。

2 灰色数列预测

以南二采区南翼－796m水平为例，本文主要从理论上对该区域2013年的涌水量进行分析预测，利用灰色理论对2013年上半年已观测得到的涌水量数据进行分析，从而建立GM（1，1）模型，并结合最小二乘法对时间t（月）和涌水量（Q）的函数关系进行拟合，求解出相应的函数关系式，进而预测矿井的涌水量。

2.1 灰色数列预测原理

灰色数列预测在形式上，只运用预测对象自身的时间序列，而与预测对象相关联的其它因素没有参与运算和建模，灰色系统理论把影响客观系统的诸多因素及它们之间的关系定为灰色量。对这样的灰色量进行预测，就可以从自身的时间序列中寻找有用信息，发现内在规律，建立模型进行预测。其中GM（1，1）模型是灰色理论中应用最广泛的一种灰色动态预测模型，该模型由一个单变量的一阶微分方程构成。它主要用于复杂系统某一主导因素特征值的拟合和预测，以揭示主导因素变化规律和未来发展趋势〔1－5〕。

2.2 GM（1，1）模型预测及算法过程

2013年1～6月份－796m水平南翼矿井涌水量见表1。

表1 2013年上半年涌水量观测值

（1）原始子数据序列

令 X（0）＝〔X（0）（1），X（0）（2），X（0）（3），X（0）（4），X（0）（5），X（0）（6）〕＝〔39.7，40.1，36.6，33.5，34.8，35.3〕

（2）对子数据序列作一次累加生成（1－AGO）即：

从而有 X（1）＝〔X（1）（1），X（1）（2），X（1）（3），X（1）（4），X（1）（5），X（1）（6）〕＝〔39.7，79.8，116.4，149.9，184.7，220.0〕

注：X（1）（1）＝ X（0）（1）

（3）定义 GM（1，1）

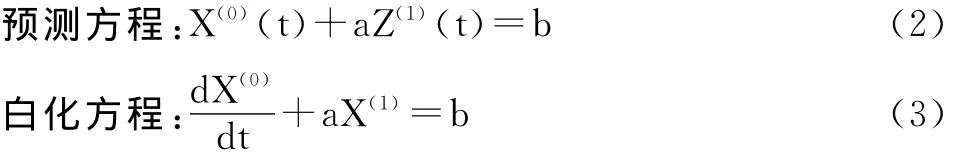
白化预测方程：

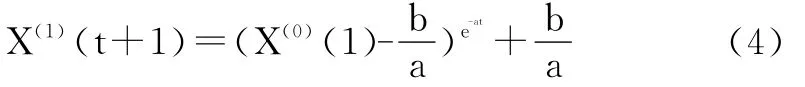
反推方程：

式中：a为发展系数；b为灰色量。

定义：

按最小二乘法求解可得：

式中：n为数据个数。

根据以上公式及数据可求解出：a＝0.0355，b＝40.756。所以：

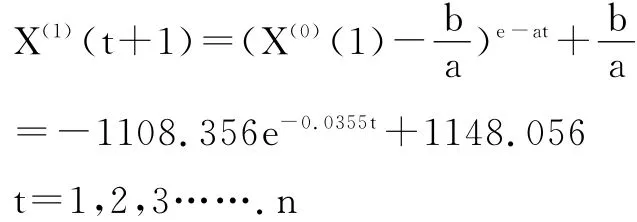
GM（1，1）是指数模型，在应用动态数据进行预测时，可对原始数据进行预处理，以便消弱数据列极值的影响，减小其随机性，强化原始数据列的大致趋势，提高预测的精度和可信度。本文采用滑动平均法来进行原始数据的预处理。

对于两端点，用下式处理：

对于中间各数据点，用下式计算其滑动平均值：

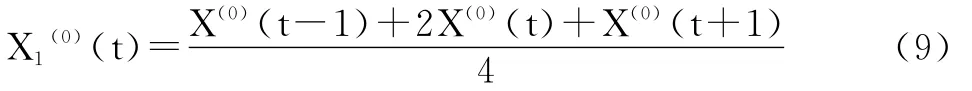
这样得到一个新的原始序列X1（0）＝ 〔39.8，35.175，39.125，36.7，34.6，34.6〕，重复上述过程可得出采用滑动平均法处理后的GM（1，1）模型，即：

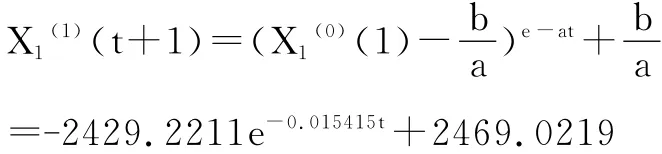
通过计算可计算出研究区在给定时间间隔内的涌水量预测值，采用原始观测值数据建模预测结果与用滑动平均法处理后建模的预测结果分别见表2、表3。涌水量Q与时间t及相对误差与时间t的关系曲线见图1～图4。

表2 采用原始数据建模的涌水量预测结果

图1 采用原始数据建模每月涌水量预测值

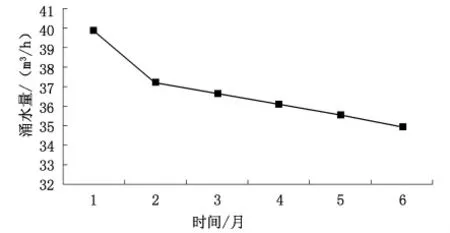
图2 采用预处理数据建模每月涌水量预测值

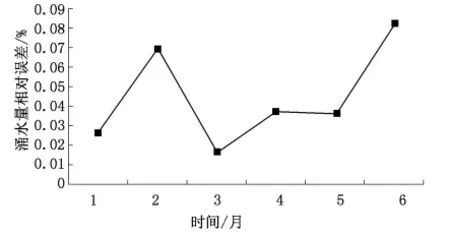
图3 采用原始数据建模涌水量相对误差随时间变化趋势

图4 采用预处理数据建模涌水量相对误差随时间变化趋势

由表1、表2及图3、图4可知，涌水量观测值与预测值的相对误差平均值分别为0.045%，0.03%。相比较而言，采用预处理后所建立的模型其预测精度较高，更符合要求。

3 结语

通过灰色理论建立GM（1，1）模型对顾桥南二采区矿井涌水量进行动态预测，预测时间内涌水量平均值分别为35.438m3／h、36.666m3／h，观测时间内平均涌水量36.667m3／h，由此可以看出经滑动平均法处理后的预测结果更为准确。该方法对矿井涌水量进行动态预测具有一定的借鉴意义。

〔1〕陈建宏，蒋 权，李贤云，等.基于Visual Modflow和灰色理论的铝土矿矿井涌水量预测〔J〕.矿业工程学院，2011，26（03）：43－47.

〔2〕李春华，李春静.GA优化GNNM（1，1）的煤矿涌水量预测〔J〕.水电能源科学，2011，29（02）：25－27.

〔3〕蔡 森，孙亚军，徐智敏，等.一种具有时空特征的工作面涌水量预测新方法〔J〕.煤矿安全，2013，44（07）：175－178.

〔4〕高志扬，徐 杰，等.基于优化GM（1，1）模型的矿井涌水量预测及算法实现〔J〕.矿业安全与环保，2013，40（01）：74－76.

〔5〕张宏刚.灰色系统模型在矿井涌水量预测中的应用〔J〕.水利科技与经济，2012，18（12）：36－38.