Optimization and coordination modelof information system security investment for interdependent risk

Gu Jianqiang Mei Shu’e Zhong Weijun

(School of Economics and Management, Southeast University, Nanjing 211189, China)



Optimization and coordination modelof information system security investment for interdependent risk

Gu Jianqiang Mei Shu’e Zhong Weijun

(School of Economics and Management, Southeast University, Nanjing 211189, China)

The impact of risk correlation on firm’s investments in information system security is studied by using quantification models combining the ideas of the risk management theory and the game theory. The equilibrium levels of self-protection and insurance coverage under the non-cooperative condition are compared with socially optimal solutions, and the associated coordination mechanisms are proposed. The results show that self-protection investment increases in response to an increase in potential loss when the interdependent risk is small; the interdependent risk of security investments often induce firms to underinvest in security relative to the socially efficient level by ignoring marginal external costs or benefits conferred on others. A subsidy on self-protection investment from the government can help coordinate a firm’s risk management decision and, thereby, improve individual security level and overall social welfare.

interdependent risk; cyber security insurance; self-protection; coordination

Various companies are subject to different types of epidemic risks such as worms, viruses and botnets. To reduce the probability of risks, they generally invest in advanced security devices such as antivirus, firewalls and intrusion detection systems (IDSs)[1-4]. However, because of the widespread usage of electronic data interchange (EDI) and the more recent vendor managed inventory (VMI) program, the security of one firm may depend on not only the security measures taken by itself but also the security measures taken by other firms. Therefore, considering a company’s information security investment strategy and security level under interdependent risk has become an important question of information security economics.

There has been a growing body of literature concerning the interdependent risk of information security. Heal and Kunreuther[5]characterized a class of interdependent security risks and demonstrated that firms generally underinvest in security relative to the social optimum.They also noted that some methods of coordination are needed to ensure that the optimum is achieved. Since then, there has been much literature specifically addressing the information security investment of interdependent organizations. Bandyopadhyay et al.[6]studied the impact of network security vulnerability and supply chain integration on firms’ incentives to invest in information security. Gao et al.[7]studied the relationship between decisions made by two similar firms pertaining to knowledge sharing and investment in information security. The analysis shows that the complementary nature of information assets possessed by the two firms plays a crucial role in influencing these decisions.

The above authors showed the existence of interdependent risk and the value of collaboration, but they did not research subsidies as a social intervention policy to induce a firm to invest at socially optimal levels and only considered self-protection as an instrument to manage risk.

In view of the self-protection inevitable barriers to 100% risk mitigation, some researchers suggested using cyber insurance, which can transfer the security risks to the commercial insurance market[8-9].Their results show that risk correlation and unproved loss cause a firm to invest less in self-protection, compared to that at the socially optimal level.

Although information security investment is a widely discussed topic among the practitioner community, very few papers have developed economic models to understand self-protection investment under interdependent risk combined with cyber insurance from the perspective of subsidy policies. The purpose of this paper is to study the role of interdependent risk in self-protection and insurance coverage of firms from a public policy perspective.Our findings suggest that the government should offer a subsidy on self-protection to achieve socially optimal results.From the interdependent risk perspective, our findings have significant implications for the design of effective public policy, if firms’ security investments cannot be coordinated.

1 Model Description

Consider two firms,iandj. The information systems of the two firms are physically connected through a communication network. The communication network is vulnerable to the propagation of security breaches from one firm to another[6]. Thus, the two firms are both subjected to direct attacks and to indirect attacks[8,10]. In order to reduce the probability of a successful invasion from hackers, it is necessary to invest in information security technology.

The probability of breach for firm,Bi(zi,zj), may depend on not only the self-protection investment of itself but also the self-protection investment of the other firm.Bi(zi,zj) can be expressed as[6]

Bi(zi,zj)=p(zi)+(1-p(zi))qp(zj)=

1-(1-p(zi))(1-qp(zj))

(1)

Note that (1-p(zi))(1-qp(zj)) is the probability that the firm does not suffer from either a direct or an indirect breach.Bi(zi,zj) has the following properties:

These properties show that an increase inqincreases the breach probability for both firms and an increase in a firm’s self-protection investment decreases its own as well as the other firm’s breach probability.

Similar to Ref.[8], we consider each firm with an initial wealthwiand utility functionU(·). We assume that both firms are rational and averse to risk, indicating that the firm’s utility function is increasing and concave (U′(·)>0,U″(·)<0) and with a constant absolute risk aversion (coefficient of risk aversion,r=-U″/U′). LetLi∈(0,ωi) denote the monetary loss associated with the threat against the information system of each firm.

We assume that there is a market for security technology and cyber insurance. Firms are able to reduce the probability of a successful invasion by investing in information security technology and are also able to transfer the information system security risk by purchasing insurance. In the cyber insurance market, the firm pays a premium ofπiIi, whereπiis the price of insurance coverage, andIiis the indemnity paid by the insurer if a security incident occurs to the firm’s information systems. But in reality, the insurance price may be expressed asπi=(1+λ)Bi(zi,zj), whereλ≥0 is the loading factor. The loading factor resembles the profitability per contract that the insurer is keen on making. If competition in the insurance market is ideal, then the loading factorλtends to 0.

Next, we consider that both firms can manage the information system risk by investing in self-protection and purchasing cyber insurance. According to this hypothesis, the firm’s utility function isUi(ωi-Li+(1-πi)Ii-zi) when it suffers a security breach and the firm’s utility function isUi(ωi-πiIi-zi) when it does not suffer any security breach.

Therefore, the expected utilityVfor firmiis given by

(1-Bi(zi,zj))Ui(ωi-πiIi-zi)}

whereBi(zi,zj)=1-(1-p(zi))(1-qp(zj)).

In the next section, we will analyze a firm’s self-protection level and insurance coverage in the non-cooperative situation and cooperative situation, and compare these two game equilibrium results.

2 Model Analysis

2.1 Non-cooperative game situation

In this section, we study the equilibrium level where the two firms cannot contract on the level of investment. Since they aim to maximize their own respective payoffs, their incentives may not be aligned. Firmi’s expected utilityVis

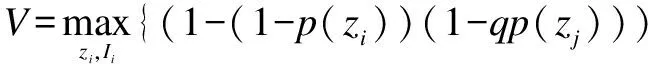
Ui(ωi-Li+(1-πi)Ii-zi)+

(1-p(zi))(1-qp(zj)Ui(ωi-πiIi-zi)}

(2)

According to Ref.[9,11], any well-behaved utility function can be expanded by a Taylor series approximation. We use the Taylor series approximation:

ωi-Li+(1-πi)Ii-zi≤ξ≤ωi-πiIi-zi

ωi-Li+(1-πi)Ii-zi≤ξ≤ωi-πiIi-zi

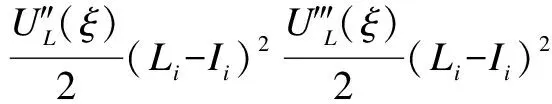
(3)

From Eq.(2), the first-order condition with respect toIican be expressed as

(1+λ)(1-(1-p(zi))(1-qp(zj))))-

(1-p(zi))(1-qp(zj)))=0

(4)

Substituting Eq.(3) into Eq.(4), we obtain

(1-(1-p(zi))(1-qp(zj)))U″L(Li-Ii)=0

Therefore, the optimal level of cyber insurance can be expressed as

After substitutingr=-U″/U′,Iisimplifies to

(5)

From Eq.(2), the first-order condition with respect tozican be expressed as

p′(zi) (1-qp(zj))(UL-UN)-

((1+λ)p′(zi)(1-qp(zj))Ii+1)((1-

(6)

Similarly, substituting Eq.(3) into Eq.(6), we obtain

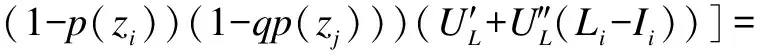
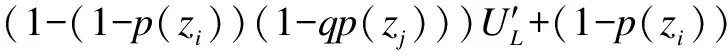
which can be further rewritten as

(7)

Substituting Eq.(5) into Eq.(7), we obtain

(8)

Symmetric parameters between the firms characterize this case:zi=zj, and the equilibrium level of insurance coverage and self-protection investment are determined by

(9)

(10)

Hereafter, we refer toISB,zSBas the optimal insurance coverage and self-protection investment in the non-cooperative situation.

Proposition 1 If the loading factor is greater than zero, then the firm buys less insurance and invests more in self-protection.

Proof Substitutingλ=0 into Eq.(10), we obtain

(11)

Proposition 2 When the interdependent risk approaches 0, the self-protection investment increases in response to an increase in potential loss.

Proof From Eq.(10), we obtain

which can be written as

Therefore,

2.2 Socially optimal self-protection and insurance coverage

If the firms can contract on the externalities, i.e. they jointly determine and implementzi,zj. In this case,zi=zj=z.

Firmi’s expected utilityVis

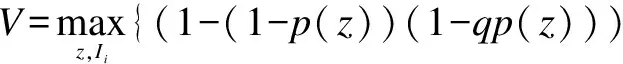
Ui(ωi-Li+(1-πi)Ii-z)+(1-p(z))·

(1-qp(z)Ui(ωi-πiIi-z)}

We also use the first-order Taylor series approximation, then the equilibrium level of insurance coverage and self-protection investment are determined by

(12)

(13)

we refer toIFB,zFBas the optimal insurance coverage and self-protection investment in the cooperative game situation.

2.3 Comparison

In this section, we compare the optimal level of investment in self-protection and insurance coverage in the non-cooperative situation with both of them in the cooperative situation.

Proposition 3 Under the non-cooperative situation, firms invest in self-protection and insurance coverage less than that of the socially optimal level.

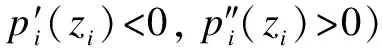
Comparing Eq.(9) with Eq.(12), sincezFB>zSB, we obtainIFB>ISB.

Proposition 3 shows that the firms invest less than the socially optimal level of self-protection. The reason is that when firms maximize their own utility, a firm does not consider the effect of marginal external costs or benefits conferred on other firms, which is an externality. Due to the complementary relationship between self-protection and insurance, the firm also buys less insurance.

3 Improving Welfare Through Subsidies on Self-Protection

In this prescriptive research, we show that under-investment in self-protection and insurance coverage relative to the socially efficient level is a common phenomenon. To solve the above mentioned problem, we design an appropriate social intervention policy to induce a firm to invest at socially optimal levels.

Assume that the government offers a subsidy ofs≤1 for each unit of investment by a firm in self-protection.In order to fund the subsidy, the government charges a lump-sum tax ofki=sizito the firm. Firmi’s expected utilityVis

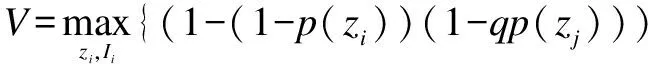
Ui(ωi-Li+(1-πi(zi,zj))Ii-(1-s)zi-ki)+

(1-p(zi))(1-qp(zj))Ui(ωi-πi(zi,zj)Ii-

(1-s)zi-ki)}

(14)

Proof The firm maximizes the expected payoff with respect toIi, then we obtain the optimal insurance coverage as

(15)

The first-order conditions with respect tozican be expressed as

p′(zi) (1-qp(zj))(UL-UN)-

((1+λ)p′(zi)(1-qp(zj))Ii+(1-s))·

(16)

Substituting Eq.(3) into Eq.(16), we obtain

(17)

Rewriting Eq.(17), we obtain

(18)

Substituting Eq.(15) into Eq.(18), we obtain

(19)

Comparing Eq.(10) with Eq.(19), we obtain

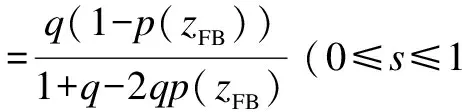
Proposition 4 shows that a subsidy on self-protection can effectively reduce the marginal cost of investment in self-protection.Through the optimal level of subsidy, the marginal revenue declines since interdependent risk is a partial offset, so as to internalize negative externalities and guide firms to invest in the socially optimal self-protection. Once the firms invest in socially optimal self-protection, the optimal insurance coverage must be purchased at the socially optimal level.

4 Numerical Analysis

We illustrate our above analysis with a numerical example and plot three figures to illustrate the above proposition.The primary purpose of the numerical analysis is to assess the impact of interdependent risk on firms’ insurance coverage and self-protection investment. For the numerical analysis, we choose the following parameters:L=0.5,p(z)=e-kz,k=3,λ=0.1,r=2. When examining the effect ofqon insurance coverage, self-protection investment and the optimal level of subsidy, we allowqto vary in the range of [0,0.1] (see Figs.1,2 and 3).

Fig.1 Impact of interdependent risk on self-protection investment

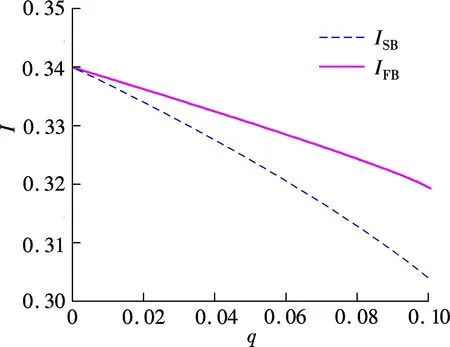
Fig.2 Impact of interdependent risk on the insurance coverage

Fig.3 Impact of interdependent risk on the optimal level of the subsidies

Fig.1 and Fig.2 show the impact of interdependent risk on the insurance coverage and self-protection investment, respectively. From Fig.1 and Fig.2, we find the following observations: 1) The firm invests less in self-protection and buys less insurance in response to an increase in the interdependent riskq; 2) In the non-cooperative situation, the firm buys less than the socially optimal insurance coverage and invests less than the socially optimal level of self-protection.

Fig.3 depicts the effect of interdependent risk on the optimal level of subsidy. We find that a high degree of interdependent risk increases the optimal level of subsidy when firms make investment decisions individually.

5 Conclusion

In this paper, we compare the optimal level of investment in self-protection and insurance coverage in the non-cooperative situation with both of them at the socially optimal level. We note that in the non-cooperative situation, individuals inefficiently underinvest in self-protection and insurance coverage. This raises the question about regulatory mechanisms that provide stronger incentives for firms to invest at the socially optimal level and, thereby, improve both individual and social welfare. We show that this can be achieved by offering a subsidy for each unit of investment by a firm in self-protection. As usual, a number of avenues remain for future research. One should consider the impact of the firms’ risk aversion on the optimum investment. Another possibility is to collect firms’ data on attack incidents, expected loss and investment, so as to prove the rationality of the social intervention policy.

[1]Gao X, Zhong W J, Mei S E. A game-theory approach to configuration of detection software with decision errors[J].ReliabilityEngineering&SystemSafety, 2013, 119(11): 35-43.

[2]Zhao L R, Mei S E, Zhong W J. Configuration strategy of two information security technologies based on risk preference[J].JournalofSystemsEngineering, 2014, 29(3): 324-333. (in Chinese)

[3]Zhao L R, Mei S E, Zhong W J. Game analysis on optimal configuration strategy of virtual private network and intrusion detection systems[J].JournalofIndustrialEngineering/EngineeringManagement, 2014, 28(4): 187-192. (in Chinese)

[4]Cavusoglu H, Raghunathan S. Configuration of and interaction between information security technologies:the case of firewalls and intrusion detection systems[J].InformationSystemsResearch, 2009, 20(2): 198-217.

[5]Heal G, Kunreuther H. Modeling interdependent risks[J].RiskAnalysis, 2007, 27(3): 621-634.

[6]Bandyopadhyay T, Jacob V, Raghunathan S. Information security in networked supply chains: impact of network vulnerability and supply chain integration on incentives to invest[J].InformationTechnologyandManagement, 2010, 11(1): 7-23.

[7]Gao X, Zhong W J, Mei S E. A game-theoretic analysis of information sharing and security investment for complementary firms[J].JournaloftheOperationalResearchSociety, 2014, 65(11): 1682-1691.

[8]Ogut H, Menon N, Raghunathan S. Cyber security risk management:public policy implications of correlated risk, imperfect ability to prove loss, and observability of self-protection[J].RiskAnalysis, 2011, 31(3): 497-512.

[9]Woohyun S. An analysis of information security management strategies in the presence of interdependent security risk[J].AsiaPacificJournalofInformationSystems, 2012, 22(1): 79-101.

[10]Zhuang J. Impacts of subsidized security on stability and total social costs of equilibrium solutions in an N-player game with errors [J].TheEngineeringEconomist, 2010, 52(2): 131-149.

[11]Schoemaker P. The expected utility model: its variants, purposes, evidence and limitations[J].JournalofEconomicLiterature, 1982, 20(2): 529-563.

风险相互依赖下的信息系统安全投资协调优化模型

顾建强 梅姝娥 仲伟俊

(东南大学经济管理学院, 南京 211189)

结合风险管理理论和博弈理论, 运用定量化模型研究了风险关联对企业信息系统安全投资的影响.通过对比非合作博弈和社会最优下的自我防御投资和网络安全保险水平, 提出相应的协调机制.研究结果表明：当关联性风险趋于很小时, 自我防御投资水平随其潜在安全损失的上升而增大;企业在进行信息系统安全投资时往往会忽略对其他企业的边际外部成本或收益的影响, 这种负外部性特征会导致企业自我防御投资和网络安全保险水平均低于社会最优化水平.政府通过补贴企业自我防御投资可以在一定程度上协调企业的风险管理决策，进而改善企业安全水平,有效提高社会福利.

风险相互依赖;网络安全保险;自我防御;合作协调

TP309

Foundation item：The National Natural Science Foundation of China(No.71071033).

：Gu Jianqiang, Mei Shu’e, Zhong Weijun. Optimization and coordination model of information system security investment for interdependent risk[J].Journal of Southeast University (English Edition),2015,31(2):288-293.

10.3969/j.issn.1003-7985.2015.02.023

10.3969/j.issn.1003-7985.2015.02.023

Received 2014-09-27.

Biographies：Gu Jianqiang (1979—), male, graduate; Mei Shu’e (corresponding author), female, doctor, professor, meishue@seu.edu.cn.