人工神经网络在聚氨酯配方设计中的应用研究

2015-05-08唐颂超徐世爱李水强

实验科学与技术 2015年1期

关键词：人工神经网络聚氨酯梯度

滕鑫，唐颂超，徐世爱，李水强

(华东理工大学材料科学与工程学院，上海 200237)

·软件开发与应用·

人工神经网络在聚氨酯配方设计中的应用研究

滕鑫，唐颂超，徐世爱，李水强

(华东理工大学材料科学与工程学院，上海 200237)

人工神经网络；BP反向传播网络；聚氨酯；应用

实验中分析处理所得到的数据往往是简单的信息。比如，在设计一种新的聚合物配方以期望达到某些特定性能指标时，往往需要在实验的基础上设计好若干份组分不同的试样进行实验，通过测试试样的性能后，再在其基础上适当调整成分或工艺参数，一般需要经过反复多次才能达到或接近预期目的。然而，有时即使是通过大量的实验也不一定能够找到理想的方案。因为，在工作中所碰到的大多数问题都是非线性的多变量的问题，简单的数据处理方法，往往只是把复杂的非线性的多变量的问题简化为简单的单个变量或者两个变量的问题。所以，面对这类实际生产中的问题，必须改变处理数据的方法[1]。在材料科学的研究中，优化算法在材料工程中取得了一定的进展，比较活跃的领域有计算材料(computational materials science)和人工神经网络[2](artificial neural networks)。

1 人工神经网络理论

人工神经网络就是所谓的神经网络，它是对人脑的抽象、简化和模拟仿真。神经网络的研究是从人脑的生理结构出发来研究人的智能行为,模拟人脑信息处理的功能，是根植于神经科学、数学、统计学、物理学、计算机科学及工程学科的一门技术[3]。

BP算法是用于多层网络的学习算法[4]，它含有输入层、输出层以及处于输入、输出层之间的中间层。中间层有单层或多层，由于它们和外界没有直接的联系，故也称为隐含层。在隐含层中的神经元也称隐单元。隐含层虽然和外界不连接，但是它们的状态会影响输入、输出之间的关系。即是说，改变隐含层的权系数，可以改变整个多层神经网络的性能。

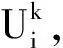
1)对权系数Wij置初值。对各层的权系数Wij置一个较小的非零随机数，但其中Win+1=-θ。

2)输入一个样本X=(x1，x2，…，xn，1)，以及对应期望输出Y=(Y1，Y2，…，Yn)。

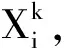
4)求各层的学习误差dik，对于输出层有k=m，有：

对于其他各层，有：

5)修正权系数Wij和阀值θ。

6)当求出了各层各个权系数之后，可按给定品质指标判别是否满足要求。如果满足要求，则算法结束；如果未满足要求，则返回3)执行。

这个过程，对于任一给定的样本Xp=(xp1，xp2，…，xpn，1)和期望输出Yp=(Yp1，Yp2，…，Ypn)都要执行，直到满足所有输入、输出要求为止。

2 聚氨酯配方实验设计

主要是考察聚氨酯配方中的异氰酸酯含量、加工温度、试用期、后固化温度及比重等五个因素对力学性能的影响[5]。法国博雷公司共制备了12组实验样本，测得数据如表1所示。将这些数据进行神经网络训练，再利用训练好的网络模型，能够比较准确地预测聚氨酯未知配方的力学性能。

表1 聚氨酯制备工艺参数与获得的材料的100拉伸强度值

为了消除不同因子之间由于量纲和数值大小的差异而造成的误差，以及由于输入变量过大造成的学习溢出的问题，需要对原始数据进行归一化处理。将实验数据按照下列公式计算[6]：

式中：xN表示归一化处理后的值，其值在[0，1]之间；x表示原来的值，xmax和xmin分别表示数组中的最大值和最小值。

归一化处理完后，还要选择几组数据作为验证数据，检验网络的具体训练情况，看是否能达到训练的预期。表2和表3即为训练数据和测试数据。

利用人工神经网络技术，采用Matlab软件[7]设计BP网络模型，建立聚氨酯配方组分与其材料力学性能的复杂的非线性关系。

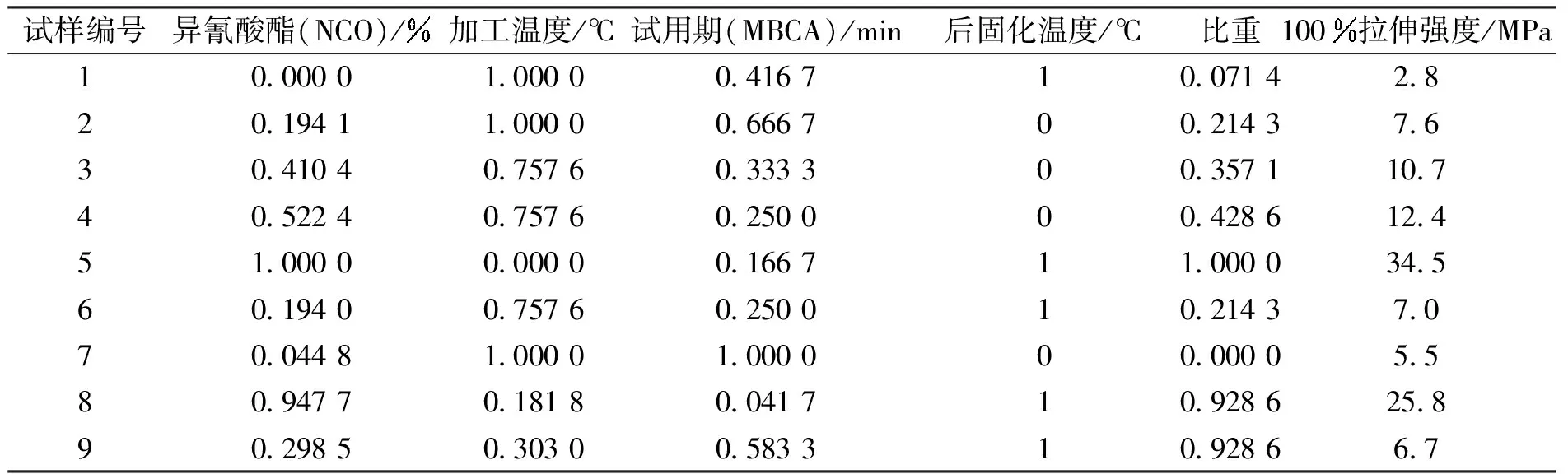
表2 经过归一化处理的学习训练数据样本集

表3 经过归一化处理的测试数据样本集

1)定义输入、输出样本向量

2)定义测试样本数据

ptest=[x(:,1),x(:,2),x(:,3),x(:,4),x(:,5);]′

ttest=x(:,6)′

3)构建一个新的BP网络

inputbias=net_1.b{1}

layerbias=net_1.b{2}

net_1.trainParam.lr = 0.05;

net_1.trainParam.mc = 0.9;

4)对网络进行训练

5)训练结束后，对网络进行仿真

A = sim(net_1,p);

6)应用均方误差(MSE)函数计算仿真误差，评价网络训练情况

E = t - A;

MSE=mse(E)

7)将检验数据输入网络，查看检验向量输入网络，评价网络

rtest = sim(net_1,p);

rdelta = rtest-t;

result_test = sim(net_1,ptest);

delta = result_test-ttest;

result=[ttest′ result_test′ delta′];

3 聚氨酯配方设计实验部分

3.1 神经网络的学习训练阶段

运行编好的程序段要解决两个比较重要的问题：网络隐含层节点数的确定和网络训练方法的合理选择。隐含层节点数的选择是一个非常复杂的问题[8]，且目前并没有统一的理论指导[9]。隐含层单元数目与问题的要求、输入/输出单元数都有直接关系。隐含层单元数太少，网络可能训练不出来，或网络容错性差；但隐含层单元数太多又使学习时间过长，误差也不一定能达到最佳。一般情况下，仅能靠经验和实验来确定隐含层单元数。将训练方法进行适当的更改，我们选择标准的梯度下降算法，在newff函数中，设定学习训练算法为traingd。采用使隐含层单元数可变的变结构法，即开始放入比较少的隐含层单元数，学习一定次数后，若不成功，就增加隐含层单元数[10]，一直达到比较合理的隐含层单元数为止。

通过计算结果得出，当节点数达到10时，曲线已经能够完美达到训练预期，收敛速度比较快且没有出现曲线波动、震荡剧烈等情况，如图1所示。

图1 隐含层节点数为10时的MSE曲线图

BP网络的训练就是网络的自学习过程，一般BP网络的训练算法是标准的梯度下降法[11]。标准的梯度下降法在调整权值时，仅仅按照当前时刻的负梯度方向进行调整，并没有考虑以前各次运算步骤中的梯度方向。因此，新的样本对迭代过程影响太大，易陷入局部极小点，导致不稳定和收敛速度慢的问题。为此，人们提出了多种高效BP算法来避免局部最小和提高收敛速度的改进方法[12]，包括：(1)加动量算法。为了加速算法的收敛速度，可考虑一动量项常数μ，动量项的贡献就是在权值调整的过程中，保存了上一个循环中的值。由于加入了以前梯度的贡献，就相当于给迭代过程添加了一个低通滤波器。(2)可变学习速率的梯度下降算法。将学习速率设定为可变，就可以改善训练算法的性能。具备自适应学习速率的梯度下降算法可以在保持训练过程稳定的前提下采用最大的学习速率。(3)牛顿法。常规的BP算法修正权值只是用到了误差函数对权值的梯度，即一阶导数的信息。如果采用二阶导数信息进行权值调整(即牛顿法)，即可以加速收敛。

这些算法都各有优缺点，但是对于一个具体的网络，就必须去找到一个合适的算法。本文根据网络训练的收敛速度、训练曲线的稳定情况及网络的仿真情况来确定适用于样本数据的网络训练算法，也就是标准梯度下降算法。

通过使用各种算法实际训练网络的情况来看，有动量的梯度算法和可变学习速率的梯度下降算法，网络的收敛速度相对比较慢，且可变学习速率的梯度下降算法MSE曲线有震荡，而牛顿法虽然迭代速度较快，但是误差下降波动剧烈，最后，标准梯度下降算法需要通过2 342次迭代，就能达到目标期望，且曲线稳定。综上所述，对于本文的样本参数，选择标准梯度下降算法来进行网络训练。因为，对所选取的样本参数，标准梯度下降算法已足够达到训练预期，且没有出现局部最小和收敛过慢。

图2～图5是各种训练算法的实际MSE曲线图。

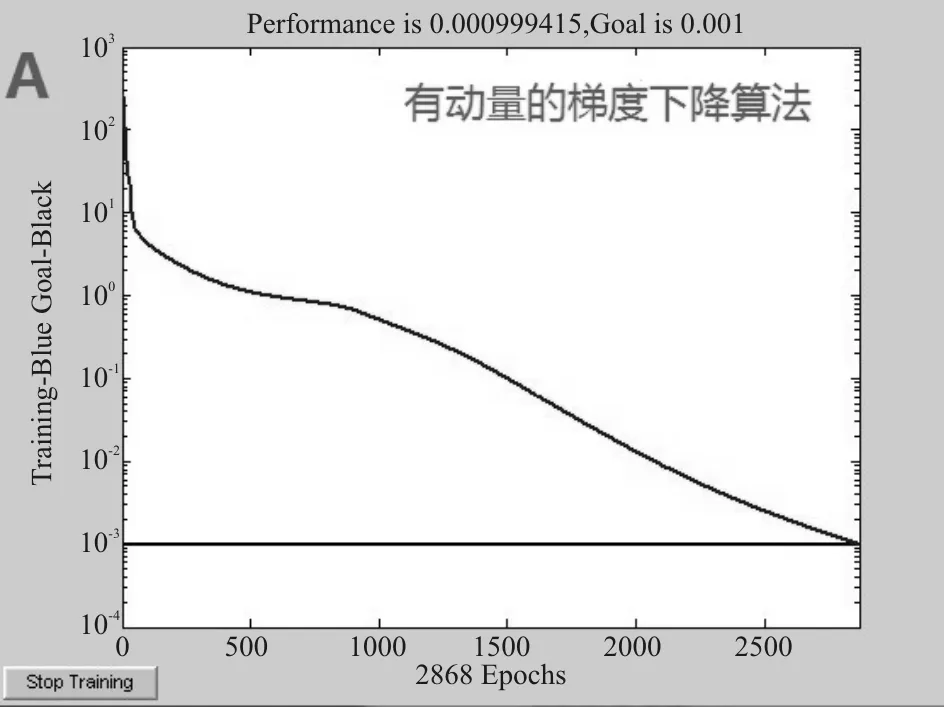
图2 有动量的梯度下降算法的MSE曲线图

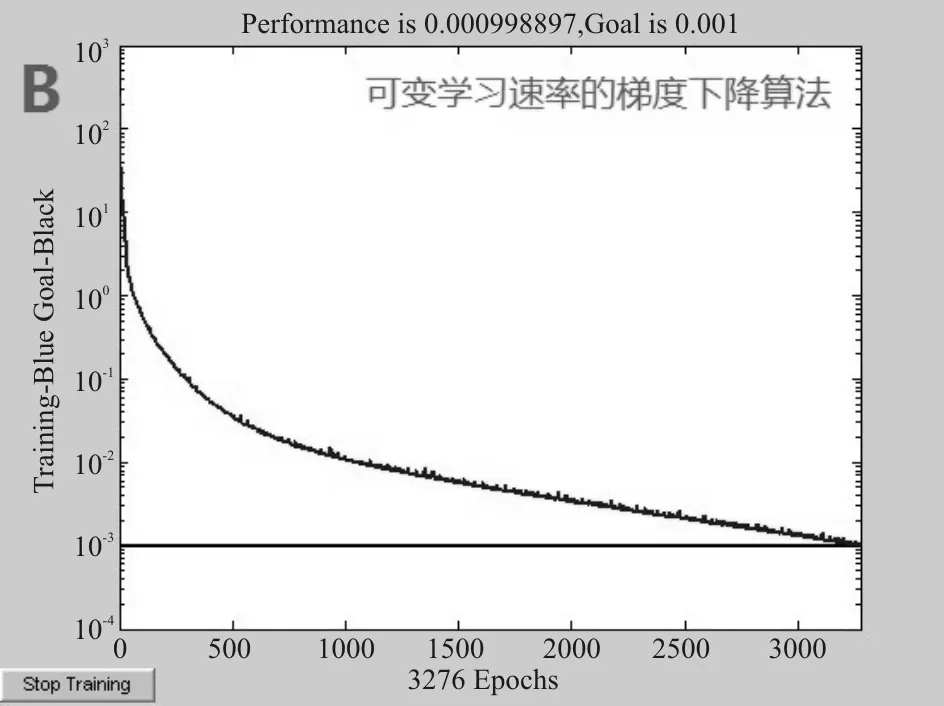
图3 可变学习速率的梯度下降算法的MSE曲线图

由于BP神经网络每次初始化权值是随机的[13],就导致了每一次训练网络时的结果会略微不同，这也是正常的情况，可以通过多次训练，寻取训练得比较好的结果。用这套训练最好的网络进行后面的性能预测，先后进行8次网络训练，记录结果如表4所示。

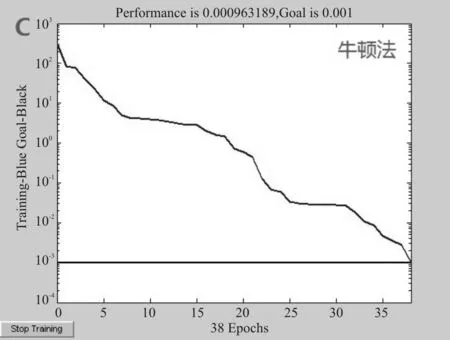
图4 牛顿法的MSE曲线图

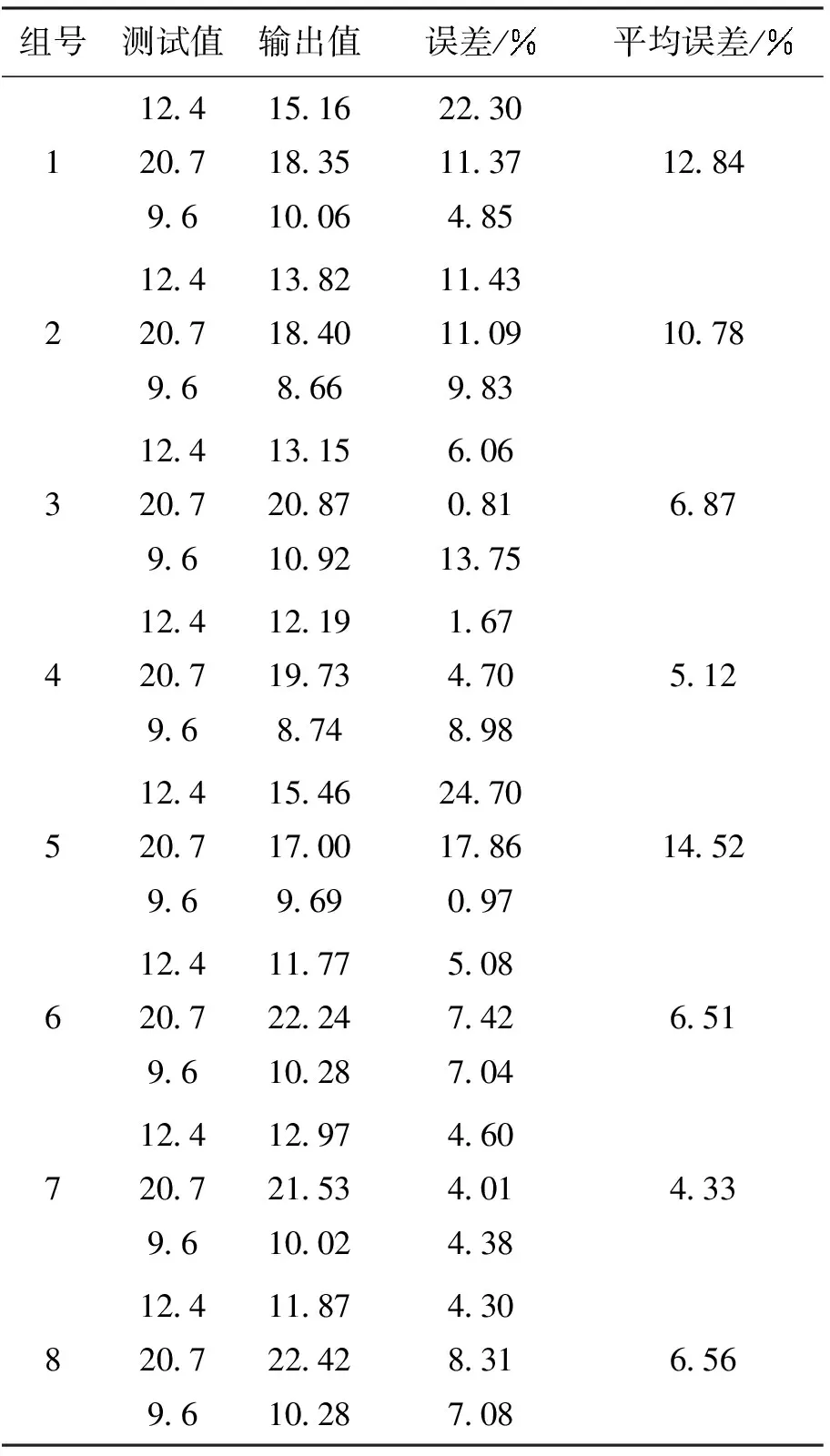
组号测试值输出值误差/平均误差/1124207961516183510062230113748512842124207961382184086611431109983107831242079613152087109260608113756874124207961219197387416747089851251242079615461700969247017860971452612420796117722241028508742704651712420796129721531002460401438433812420796118722421028430831708656

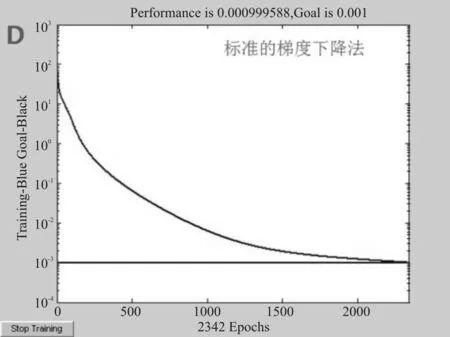
图5 标准梯度下降算法的实际MSE曲线图

通过比较，发现第七次网络训练比较好，误差控制小，精度高，所以选择第七次训练的网络来进行性能的预测。

3.2 神经网络的预测阶段

现在就能利用已经训练好的神经网络进行对未知配方的拉伸强度的性能测试了。可以任意确定一个配方参数：异氰酸酯、加工温度、试用期(MBCA)、后固化温度、比重，[8.12，75，5，100，1.1]。把这个参数进行归一化处理之后得：[0.794 0，0.454 5，0.25，1，0.214 3]，再在程序后面输入：

sim(net_1,x)