基于Stearns-Noechel优化模型的交织混色织物配色设计系统

章斐燕, 李启正, 张声诚, 祝成炎

(1.浙江理工大学 现代纺织加工技术国家工程技术研究中心, 杭州 310018; 2.浙江三志纺织有限公司,浙江 湖州 313100)

研究与技术

基于Stearns-Noechel优化模型的交织混色织物配色设计系统

章斐燕1, 李启正1, 张声诚2, 祝成炎1

(1.浙江理工大学 现代纺织加工技术国家工程技术研究中心, 杭州 310018; 2.浙江三志纺织有限公司,浙江 湖州 313100)

针对目前开发交织混色配色系统的需要，在Stearns-Noechel模型的基础上，通过标准样和单色纱的光谱反射率计算，结合计算机配光谱法中的配反射率法，利用色差宽容度和迭代修正误差的方法，控制配色方案中的匹配样与标准样的色差。系统应用结果表明：该系统能够快速地预测已知交织混色织物的配色设计方案，输出具体的色纱种类、色纱在织物表面的覆盖率等；将计算得到的配色方案与数据库匹配或自定义参数可获得织物经纬密度、经纬纱线线密度、组织图等，当参数设置不同时所需的组织图也不同，这在增加配色方案多样性的同时也提高了自主选择性。

Stearns-Noechel模型; 交织混色; 色织物; 配色; 几何模型

交织混色织物一般指采用有色或染色纱线进行交织的机织物，不同的纱线排列和不同的组织结构可以获得各种不同的织物色彩效应[1-2]。目前，越来越多的企业利用色纱交织得到具有不同色彩效果的面料。然而，如何通过色纱和组织图的选择、上机参数的设置等，获得与标准样(或目标色)一致的颜色，却一直是配色工作中存在的难点。

目前，国内外的研究主要以纤维混色[3-4]、配料[5-6]和混色织物的颜色预测模型[7-8]为主，关于混色织物的配色设计方面甚少有报道，目前也没有相关的系统和软件。因此，本研究着重于实现基于Stearns-Noechel优化模型的交织混色织物的配色设计系统，实现颜色配色方案和织造所需参数的计算等功能，为交织混色织物配色系统的进一步开发提供参考。

1 交织混色织物配色的基础理论

1.1 几何模型

在进行交织混色织物的颜色预测时，需要根据几何模型[9]计算色纱在织物表面的颜色覆盖率，因此，几何模型的精确度在一定程度上决定了颜色预测的准确性，在该模型中假设纱线截面是理想的圆形。通过式(1)～(4)计算色纱在织物表面的覆盖率，以2/2组织图为例的组织结构如图1所示。

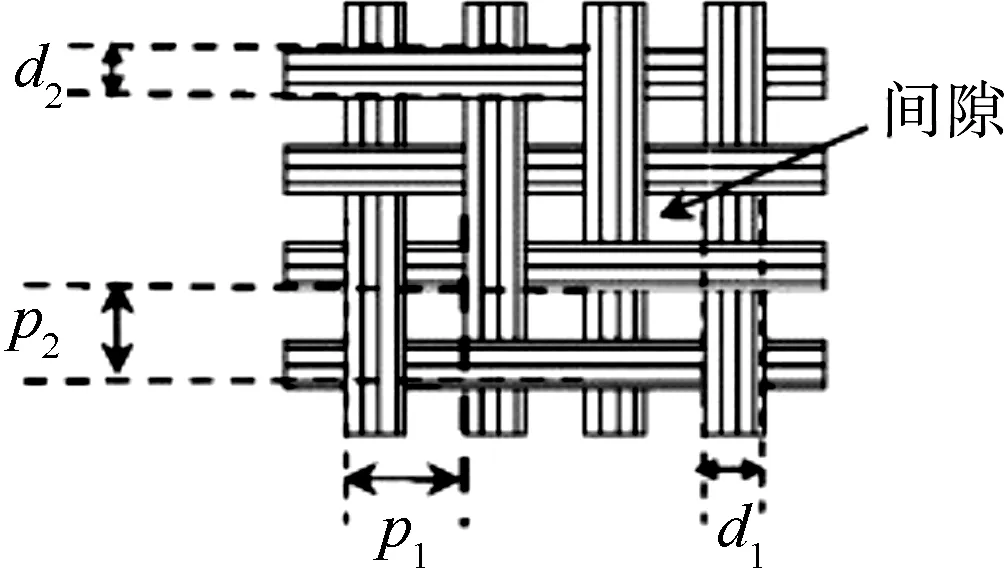
图1 组织结构示意Fig.1 Weave structure diagram

(1)

(2)

(3)

(4)

式中：d为纱线直径，mm；Ntex是纱线线密度；δ是纱线体积密度，g/cm3；n1是经组织点个数；n2是纬组织点个数；m1是一个组织循环内的经纱根数；m2是一个组织循环内的纬纱根数；d1是经纱直径；d2是纬纱直径；p1是经纱间距；p2是纬纱间距；x1是经纱在织物表面的覆盖率；x2是纬纱在织物表面的覆盖率；xb是织物的间隙率。

1.2 Stearns-Noechel模型

1944年，Stearns和Noechel[10]利用羊毛混色实验建立了混色样的反射率与组成混色的单色反射率间的数学关系，假设式(5)成立，从而提出了式(6)：

(5)

(6)

式中：f[R(λ)]是Stearns-Noechel模型公式；Rblend(λ)是波长为λ时的混合色的反射率；Ri(λ)是波长为λ时第i组分纤维的反射率；xi是第i组分纤维的质量比例；b是唯一可变常数，其值与选用的纤维原料有关，不同纤维原料的b值大小需通过实验来确定。

由于参数b是根据实验确定的，当实验原料不同时，其取值也不同。根据现有文献[3]和[10-12]分析，针对不同的纤维，参数b的取值如表1所示。

表1 文献中不同纤维在Stearns-Noechel模型中的参数

2 基于Stearns-Noechel模型的光谱配色算法

2.1 初始配方计算

由于反射率R与K/S值一一对应，配光谱法又可分为配K/S值法和配反射率法两种。以配反射率法为例，其原理是将匹配样的光谱反射率与标准样的光谱反射率相匹配，即需满足：

(7)

假设在一定波长下，交织混色织物的表观颜色由单纱在织物表面的覆盖率和单纱颜色决定，则下式成立：

(8)

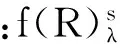
以2种单色纱线交织的色织物配色为例，选择波长为380～700nm，间隔10nm，具体计算公式如下：

(9)

(10)

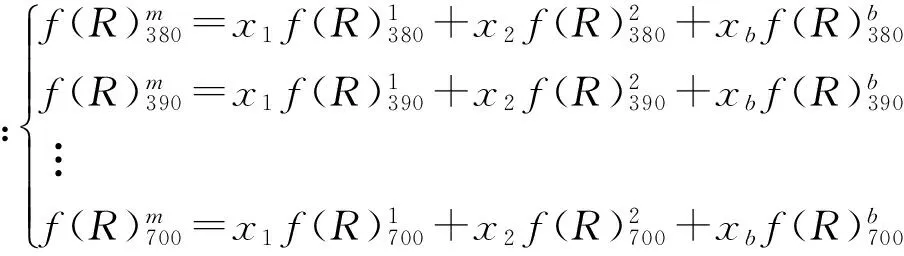
因此：Fs=Fm=FX

(11)

由于式(11)中有33个方程，当求解3个未知量时方程组有多个解，且在实际运算中，方程左右两边不一定完全匹配，因此，本文选用最小二乘法解方程组：

(12)

X=(FT×F)-1×FT×Fs

(13)

式中：FT为矩阵F的转置矩阵；(FT×F)-1为矩阵(FT×F)的逆矩阵；X即为解得的各单纱在织物表面的覆盖率x1、x2，以及织物的间隙率xb。

2.2 迭代修正计算

基于Stearns-Noechel模型，运用配光谱法可推算出各单纱在织物表面的覆盖率，获得初始配方。当初次配色不成功时，需要利用迭代法进行修正：

式中：列矢量Ft表示初始配方样的f(R)λ值；ΔT表示初始配方样的反射率与标样的反射率的差异；ΔX表示修正配比量。

为了提高配方计算的准确性，ΔX是使ΔT减少到零的修正变量，因此：

(14)

ΔT=Fs-Ft=FΔX

(15)

2.3 评价指标与色差公式

3 交织混色织物配色系统

3.1 配色系统的算法流程

图2 交织混色织物配色系统的算法流程Fig.2 Arithmetic process of color matching system for color mixed interwoven fabrics

3.2 配色系统的应用

为了验证交织混色织物配色系统的精确性和实用性，对以涤纶原液染色长丝为原料的色织物进行配色。根据本课题组的前期研究，对288块以原液染色涤纶长丝为原料的交织混色织物样品(具体规格如表2所示)求解平均色差最小时的b值，结果表明当b为0.021时试样的平均色差最小。其中，以米色经纱、蓝色纬纱的交织混色织物为例，随机抽取5个试样进行测量比对，结果如表3所示。试样1的系统显示结果如图3所示。

表2 织物规格

表3 5个随机试样的比对结果

注：色差1是指根据系统配色比例得出的预测颜色值与标样颜色值间的色差；色差2是指根据纱线线密度、经纬密度等参数反推出组织图，再计算得出的预测颜色值与标样颜色值间的色差。

图3 系统显示结果示意Fig.3 Schematic diagram of system display results

从表3可知，随机抽取的5个试样其系统配色比例与织物实际颜色比例相近，且色差值基本控制在0～3以内。色差1的产生主要是由于交织混色织物在织造过程中本身存在均匀程度的误差，因此在配色比例的推导中存在一定的误差；而色差2的产生主要是由于在纱线几何模型中，假设纱线截面为理想圆形，而在实际生产过程中，纱线截面并非呈圆形，而是椭圆、扁平等不规则形状。这也是今后需要致力于研究的方向之一。

由图3可知，系统给出的配色结果包括标准样的颜色值、匹配样中的各单色纱的颜色值和预测比例、标准样与匹配样的色差、各颜色最接近的Pantone TPX色号等。系统运算得到的配方可以根据数据库进行匹配，得到织物的参数和组织图；也可以自行设置参数，在组织库中进行组织图匹配。当自定义时，系统可以根据参数设置的不同而提供多种配色结果，根据企业的实际情况进行方案的选择，提高交织混色织物的配色效率，从而提高企业对市场的反应能力，增强企业的竞争力。

4 结 语

经过系统的初步应用可知，通过VB程序语言开发的基于Stearns-Noechel模型的交织混色织物配色系统，能够快速地预测配色方案，输出具体的织物参数、组织图、色纱种类等；也可以通过自定义参数得出不同的方案，在增加配色方案多样性的同时提高了企业的自主选择性。根据本系统的配色方案，可以提高交织混色织物的打样效率，缩短企业的生产周期，从而更好地实现对市场的快速反应和占领。

[1]NG M C F, ZHOU J. A study on figured double-face jacquard fabric with full-color effect[J]. Textile Research Journal,2009,79(10):930-936.

[2]ZHOU J. Digital jacquard fabric design in colorful mode[J]. Journal of Donghua University,2004,21(4):98-101.

[3]PHILIPS-INVERNIZZI B, DUPONT D, JOLLY-DESODT A M, et al. Color formulation by fiber blending using the Stearns-Noechel model[J]. Color Research & Application,2002,27(2):100-107.

[4]李戎,宋阳,顾峰.基于Stearns-Noechel模型的纤维光谱配色算法[J].纺织学报,2007,28(1):77-80. LI Rong, SONG Yang, GU Feng. Spectrophotometric algorithm of pre-colored fiber based on Stearns-Noechel model[J]. Journal of Textile Research,2007,28(1):77-80.

[5]陈维国,周华,温泉,等.羊毛混色纺纱计算机智能测色配料系统[J].毛纺科技,2010(4):48-52. CHEN Weiguo, ZHOU Hua, WEN Quan, et al. Intelligent color matching system of wool blending yarn[J]. Wool Textile Journal,2010(4):48-52.

[6]沈加加,程凤侠,陈维国,等.Stearns-Noechel模型优化及毛条混色配色系统开发[J].纺织学报,2009,3(3):121-125. SHEN Jiajia, CHENG Fengxia, CHEN Weiguo, et al. Development of color matching system for pre-colored wool top blends by optimized Stearns-Noechel model[J]. Journal of Textile Research,2009,3(3):121-125.

[7]王春燕,刘阳,李丹,等.纬全显色提花织物的混配色算法研究[J].浙江理工大学学报,2012,29(3):307-310. WANG Chunyan, LIU Yang, LI Dan, et al. Research on the color-match algorithm of pre-colored weft-all-coloring jacquard fabric[J]. Journal of Zhejiang Sci-Tech University,2012,29(3):307-310.

[8]MATHUR K. Color Prediction Model for Jacquard Tapestry Woven Fabrics[D]. Raleigh NC: North Carolina State University,2007:110-139.

[9]MATHUR K, HINKS D, SEYAM A F M, et al. Towards automation of color/weave selection in jacquard design: model verification[J]. Color Research & Application,2009,34(3):225-232.

[10]STEARNS E I, NOECHEL F. Spectrophotometric prediction of color of wool blends[J]. American Dyestuff Reporter,1944,33(9):177-180.

[11]DAVIDSON H R, TAYLOR M. Prediction of the color of fiber blends[J]. JOSA,1965,55(1):96-98.

[12]BURLONE D A. Theoretical and practical aspects of selected fiber-blend color-formulation functions[J]. Color Research & Application,1984,9(4):213-219.

Color Matching System for Colored Interwoven Fabrics Based on Optimized Stearns-Noechel Model

ZHANG Feiyan1, LI Qizheng1, ZHANG Shengcheng2, ZHU Chengyan1

(1.Modern Textile Processing Technology National Engineering Research Center, Zhejiang Sci-Tech University, Hangzhou 310018, China;2.Zhejiang Sanzhi Textile Co.,Ltd., Huzhou 313100, China)

In allusion to the need of developing interwoven color matching system, based on Stearns-Noechel model, this paper combines the reflectivity matching method in computer spectral matching method, color tolerance, iterative correction method to control chromatic aberration between matching sample and standard sample in the color matching scheme through calculating spectral reflectance of standard sample and single-colored yarn. System application results show that, this system can quickly predict the color matching design scheme of known interwoven multi-color fabrics, and output specific dyed yarn types and coverage of dyed yarns on fabric surface etc. Thread count, thread denier, weave diagram and so on can be obtained through matching color matching scheme and database or self-defining parameters. When parameters are set differently, weave diagrams are also diverse. This improves autonomous selectivity while adding color matching scheme diversity.

Stearns-Noechel model; interwoven mixed-color; colored fabrics; color matching; geometric model

doi.org/10.3969/j.issn.1001-7003.2015.01.005

2014-07-29;

2014-10-25

国家科技部国际科技合作专项项目(2011DFB51 570)；高等学校博士学科点专项科研基金联合资助课题项目(20123318110003)

章斐燕(1990-)，女，硕士研究生，研究方向为纺织CAD技术。通信作者：祝成炎，教授，cyzhu@zstu.edu.cn。

TS105

A

1001-7003(2015)01-0026-05 引用页码: 011104