悬滴与卧滴合并行为特性

沈超群 陈永平 施明恒

(1东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(2东南大学能源与环境学院, 南京 210096)(3扬州大学水利与能源动力工程学院, 扬州 225127)

悬滴与卧滴合并行为特性

沈超群1,2陈永平1,3施明恒1,2

(1东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(2东南大学能源与环境学院, 南京 210096)(3扬州大学水利与能源动力工程学院, 扬州 225127)

基于VOF(volume of fluid)方法,建立了重力条件下悬滴与卧滴在空气中合并过程的理论模型，并进行数值模拟,研究了悬滴与卧滴的合并流型,并分析了不同Bond数下悬滴与卧滴的合并动力学行为.结果表明,悬滴与卧滴接触后,液滴间形成的液桥在表面张力的作用下快速扩展,在液桥与针头间出现颈缩现象;悬滴与卧滴合并过程存在“合并无断裂”和“合并后断裂”2种合并流型,当Bond数约为0.05时,合并流型由无断裂向断裂转变.随着Bond数增大,液滴合并后断裂的无量纲时间随之减小,当Bond数大于0.18,液滴合并后断裂的无量纲时间逐渐趋向定值.

液滴;合并;流型;颈部断裂

当2个液滴相互接触后,液滴将发生合并以使表面能达到最小化.液滴合并在自然界和化工生产中广泛存在,如雨滴的形成[1]、珠状凝结过程[2]、烧结过程[3]、微流体制备[4]等.同时,液滴合并过程涉及到自由界面流动、Rayleigh-Plateau不稳定性及界面奇异点动态演变等众多关键科学问题.因此,近年来液滴合并过程的研究受到了国内外研究者的广泛关注,对液滴合并动力学特性及其行为机理的揭示也愈加受到重视.

目前,采用高速测量技术与方法进行实验观测已成为研究液滴合并行为的主要研究手段,如电学方法[5]、相干X线相衬成像技术[6]和高速摄影技术[8-9]等.通过该类方法对液滴合并过程,特别是液滴合并早期过程中“液桥”的演变规律及其影响因素进行了广泛的研究.Eggers等[7]通过高速可视化观测液滴合并的早期过程发现,由于表面张力的作用,液桥处的弯月面驱动了液滴合并过程;Case等[5]利用电学方法研究了低黏度液滴合并的早期过程,研究表明液滴合并演化过程受到液滴初始形状及液滴可变形性的影响.Fezzaa等[6]则利用相干X线相衬成像技术可视化呈现了水滴在空气中合并的前期过程,发现由于液滴接触后快速合并,部分原先液滴间的空气被包裹形成弧形汽泡,直至约400 μs以后汽泡排出.Thoroddsen等[8]和Wu等[9]通过观测不同条件下液滴合并初期液桥半径的动态演化发现,在此阶段内桥半径的变化符合Rb∝t1/2(Rb为桥半径,t为合并演化时间)规律.此外,部分研究者还初步探索了液滴在倾斜表面[10]和超疏水表面[11]的合并及弹跳行为特性与规律,这些研究为液滴合并行为特性的研究拓展了思路.

除了实验研究外,国内外研究学者还从理论角度对液滴合并行为特性尤其是液滴合并初期液桥形成与动态演化过程进行了研究.Duchemin等[12]采用高精度边界积分方法,理论分析了平板上2个液滴在忽略空气影响的条件下的合并.Menchaca-Rocha等[13]采用数值模拟方法研究了平板上的液滴合并过程,其结论与实验观测结果基本一致,桥半径的演化也符合Rb∝t1/2.Yue等[14]及Blanchette等[15]采用数值模拟方法研究了液滴与水平液-液界面或汽-液界面的合并过程,发现液滴内工质流动速度对合并后出现断裂现象有重要影响.Mohammadi等[16]也数值模拟了水滴在油中的合并过程.

综上所述,目前已有的研究主要关注液滴合并初始阶段液桥的形成及演化行为,而对液滴合并的整个过程的流型演化研究较少.同时,针对液滴合并尤其是悬滴与卧滴动态合并全过程的流型演化研究非常匮乏,且液滴合并动力学行为也尚未揭示.为此,本文采用VOF方法,数值模拟了重力条件下等直径的悬滴与卧滴在空气中的合并过程,研究了液滴合并流型,并探索了Bond数对液滴合并后断裂时间的影响.

1 数学模型

本文所模拟液滴合并的几何结构及尺寸如图1所示.计算区域为L=4 mm,H=10 mm的矩形轴对称区域(图中黑色实线与点划线内的区域),悬滴及卧滴位于计算区域中央,液滴半径为Rp=Rs=0.76 mm,针管半径为0.42 mm.液滴工质为水,初始时刻工质充满针管,液滴相互接触且接触速度为0 m/s.

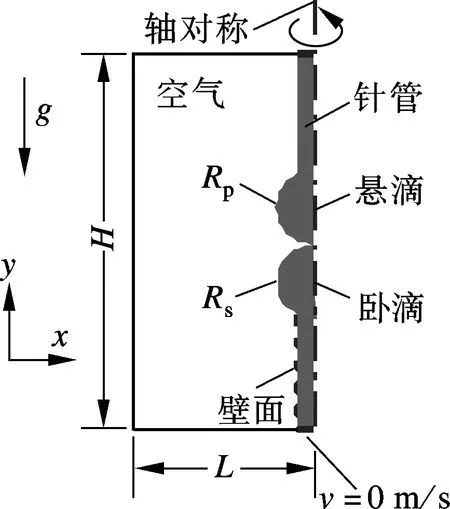
图1 计算区域及边界条件示意图

1.1 控制方程

本文采用VOF[17]方法追踪空气中液滴合并过程气/液相界面运动与演化行为.在VOF方法中,每个控制单元中各相的体积率之和为1,即

αg+αl=1

(1)

式中，α为体积率；下标g，l分别表示气相和液相.流场中αg遵循以下体积率控制方程:

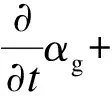
(2)

式中,v为速度.气液相界面的追踪可以通过求解体积率方程中气相体积率来实现:若控制单元中气相体积率αg=0,则此控制单元充满液相;反之,若控制单元中气相体积率αg=1,则此控制单元充满气相.气液界面存在于气相体积率为0<αg<1的控制单元中.

对于悬滴与卧滴在空气中的合并过程,气液两相流体还需满足以下控制方程:

连续性方程

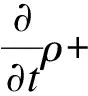
(3)

动量方程

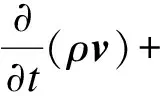
(4)

式中,ρ,μ分别为密度及黏度；g为重力加速度.计算区域的每个控制体积内流体的物性参数满足

ρ=αlρl+αgρg

(5)

μ=αlμl+αgμg

(6)

气液两相之间的表面张力则采用连续表面力(continuum surface force, CSF)[18]模型进行计算,该模型将表面张力看作是一种作用于相界面区域网格单元内流体的体积力,即

(7)

其中,界面曲率k定义为

(8)

1.2 边界条件及数值求解方法

对图1所示的区域采用四边形结构化网格进行均匀划分,经网格独立性检测后,整个计算区域的网格尺寸取为Δx=Δy=0.045 mm.边界条件设置如图1所示,计算区域的上、下及左边界采用自由出流条件;计算区域右边界采用对称轴条件;针管壁面采用无滑移壁面条件;针管入口采用速度入口条件,且速度设为0 m/s.模型求解中压力场和速度场的耦合采用引入了临近校正和偏度校正的PISO方法.为取得良好的收敛效果,计算中对控制方程中的部分参量使用了欠松弛因子：压力项为0.2，密度项为0.5,体积力源项为0.4,动量源项为0.2.计算中动量方程采用二阶迎风差分格式离散,其他方程均采用一阶迎风差分格式离散;非稳态求解的计算时间步长确定为Δt=10-6s,各参量的残差收敛标准为10-3.

1.3 模型验证

本文对Thoroddsen等[8]所开展的悬滴与卧滴合并实验进行了对比数值模拟,如图2所示.由图可见，数值模拟所得液滴合并流型与实验流型符合较好,表明本文所建的模型准确可靠.

(a) 悬滴与卧滴合并实验图像[8]

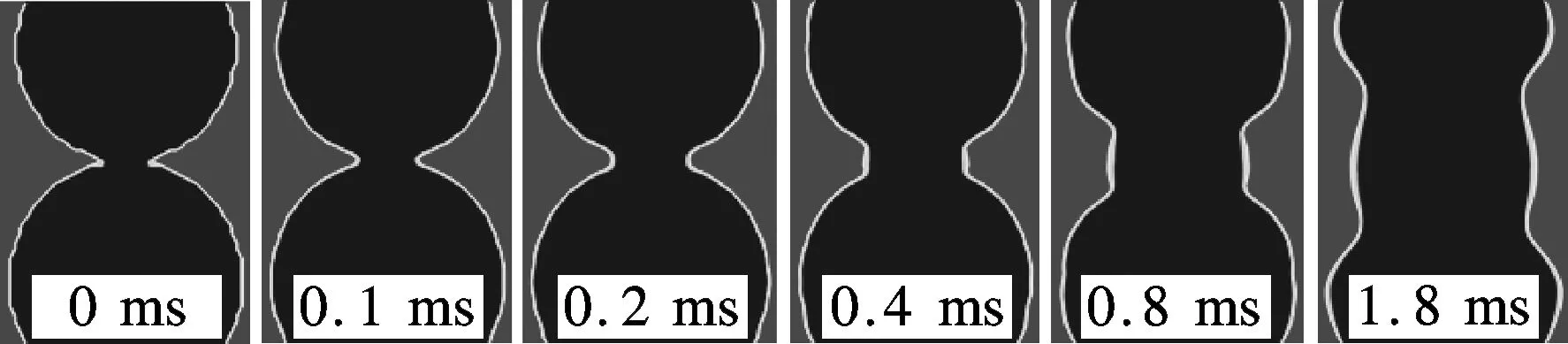
(b) 数值模拟结果

2 液滴合并流型

在重力条件下,液滴合并同时受到重力和表面张力的影响,本文以无量纲数Bond数表征重力及表面张力间的相对大小.Bond数定义为

(9)

式中,σ和R分别为气液界面表面张力系数和液滴半径.由于液相密度远大于气相密度,因此,式(9)可以简化为

(10)

以无量纲时间τ′表征液滴合并过程所持续的时间,即

(11)

式中,τ为液滴从开始接触的合并过程时间;τc为毛细时间,其表达式为

(12)

模拟结果表明,不同工况下,等直径悬滴与卧滴合并过程存在“合并无断裂”和“合并后断裂”2种流型.图3给出了当Bo=0.01时等直径悬滴与卧滴合并所出现的“合并无断裂”流型的动态演化过程.如图3所示,当悬滴与卧滴接触后,形成液桥连接液滴(图3中椭圆所示的τ′=0.23时的轮廓).在表面张力的作用下,液桥快速扩展,体积增大.同时悬滴和卧滴体积减小,在液滴和针管间形成颈部(图3中矩形框所示的τ′=2.38时的轮廓).此后,合并后的液滴逐渐振荡松弛,最终悬挂于2个针管之间(如图3中τ′=172.70所示的液滴轮廓),未出现断裂现象.

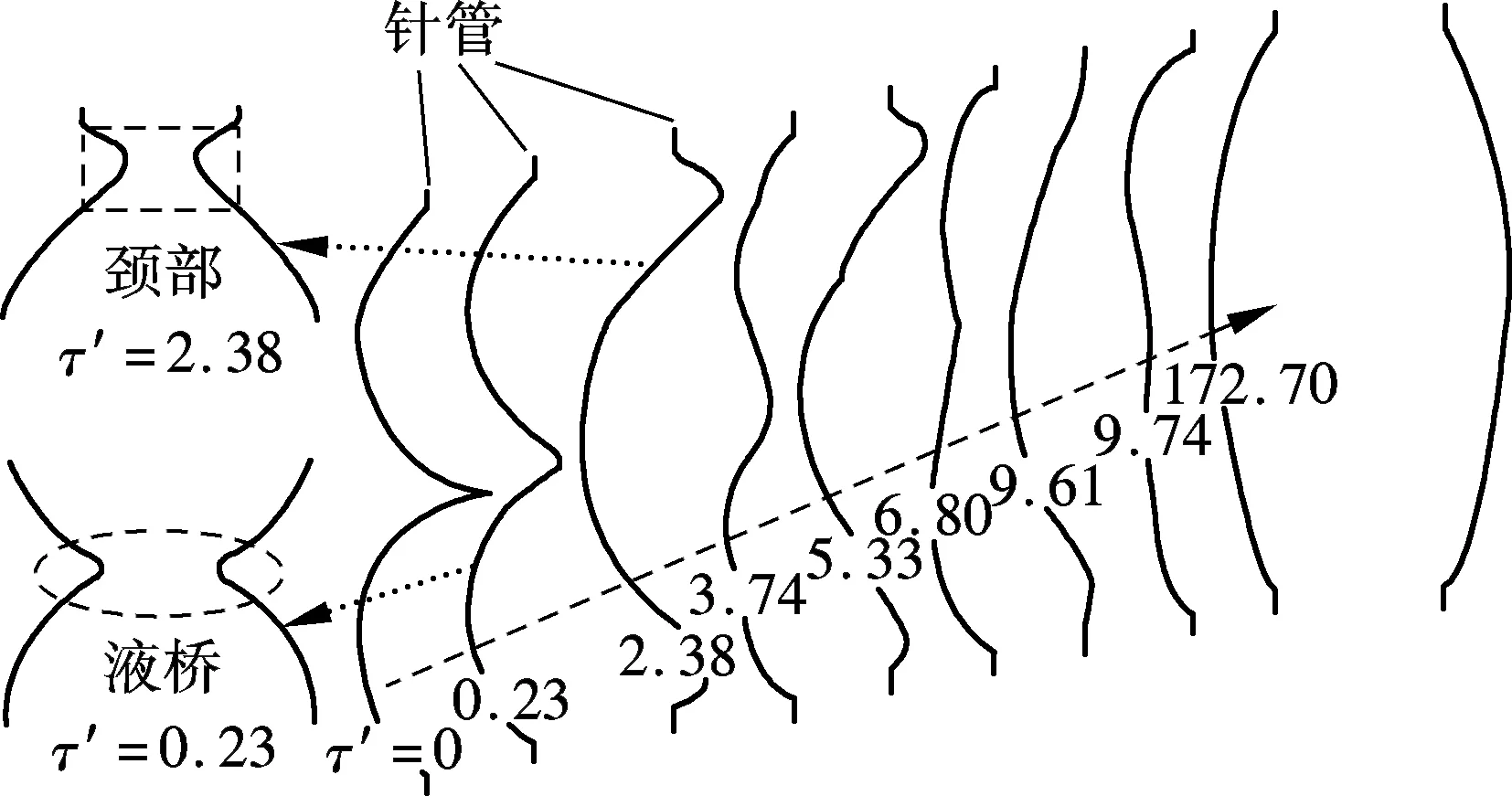
图3 合并无断裂流型的轮廓演化过程(Bo=0.01)

随着Bond数的增加,液滴合并过程中重力的作用越来越明显.对比图4与图3中液滴合并后轮廓演化过程可见,大Bond数工况下,由于重力作用增强,合并后液滴内工质在重力的作用下更快地向卧滴流动,靠近上方针头处形成的颈部更细,并最终断裂,而出现“合并后断裂”的流型.图5给出了合并后断裂流型下的液滴内部压力及速度分布.数值计算结果表明,对于出现断裂的合并流型,颈部区域内在表面张力的作用下出现了高压区,在压力驱动下液体流出颈部,颈部不断变细,最终出现断裂现象.

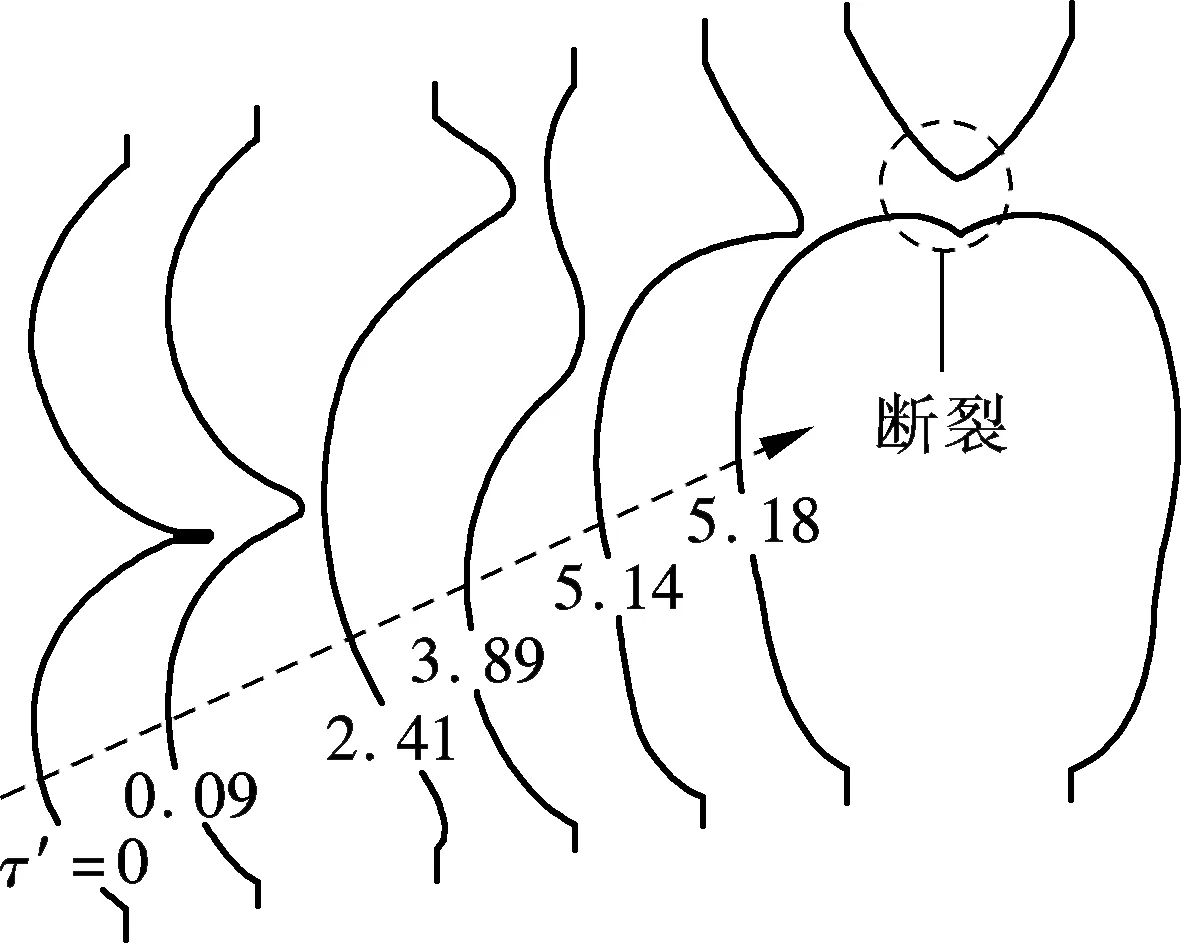
(a) Bo=0.06

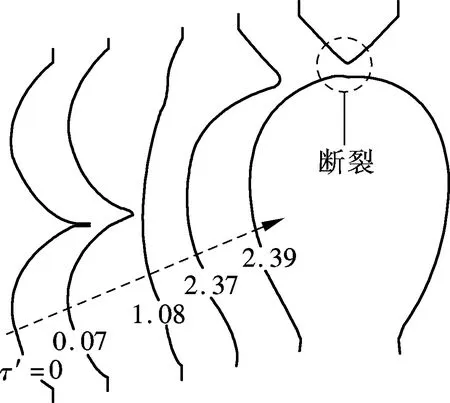
(b) Bo=0.1

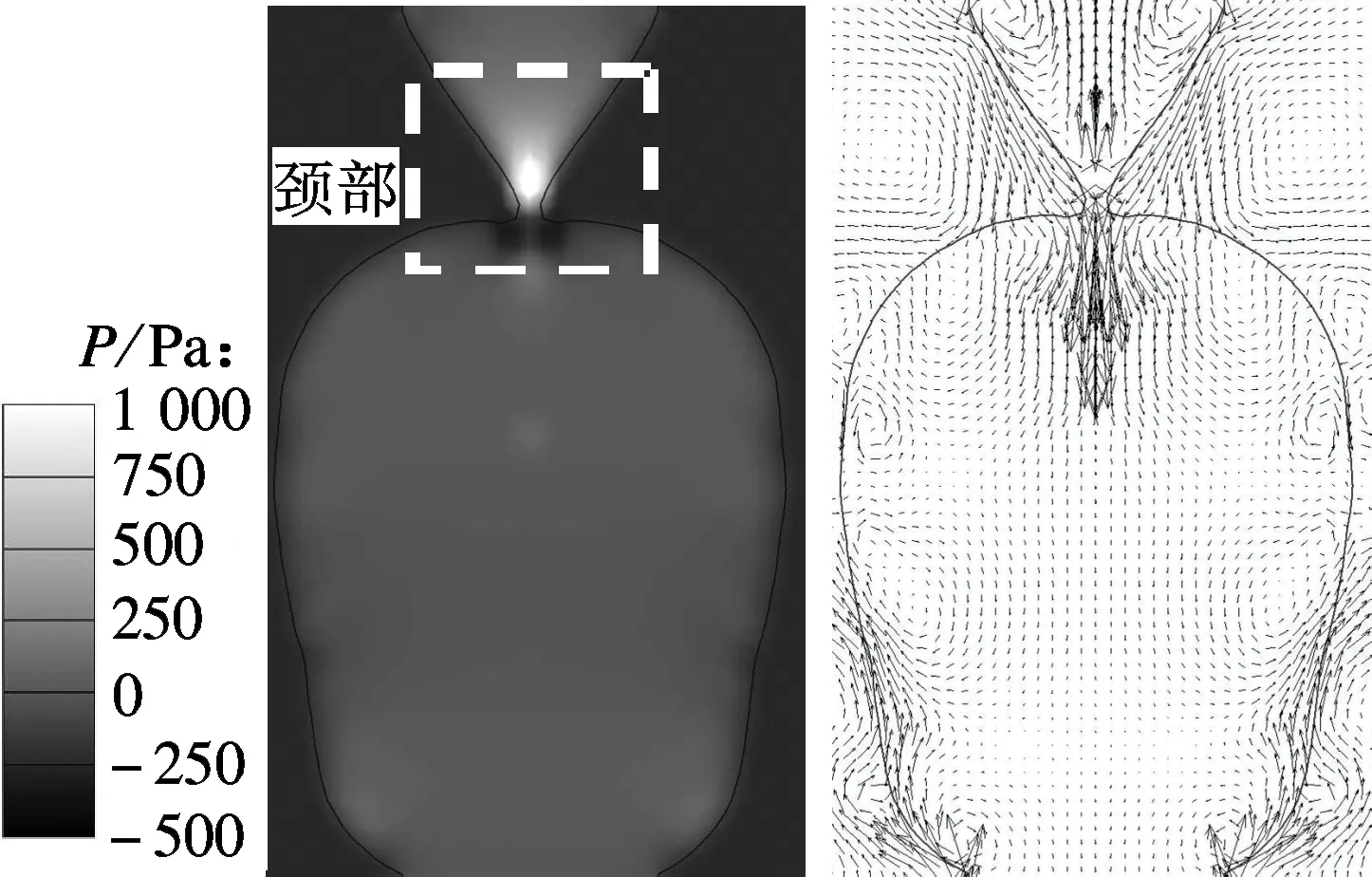
图5 合并后断裂时液滴内压力及速度分布(Bo=0.06,τ′=5.14)

表1给出了不同Bond数下,等直径悬滴与卧滴合并的流型.随着Bond数的增加,等直径悬滴与卧滴合并流型由无断裂向断裂转变,也表明重力对合并过程的影响越来越明显.同时,模拟结果表明,当Bond数大约为0.05时,出现颈部断裂的合并流型.

3 Bond数对断裂时间的影响

表1 等直径悬滴与卧滴合并流型

(13)

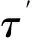
液滴合并过程中,颈部体积变化受重力和表面张力影响较明显,在二者的共同作用下颈部体积减小而断裂.液滴接触后,由于液桥处存在巨大的曲率,在表面张力的驱动下液桥体积增大,颈部体积减小,因此表面张力越大,液桥体积增大越快,颈部体积减小也越快;同时,液体在重力驱动下由悬滴向卧滴方向流动,进一步促进了液桥与上方针头间颈部体积的减小.由图4对比可见,当τ′=5.18,Bo=0.06工况时,等直径悬滴与卧滴合并后出现断裂现象,而Bo=0.1的工况下,在τ′=2.39时就出现断裂现象.

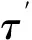
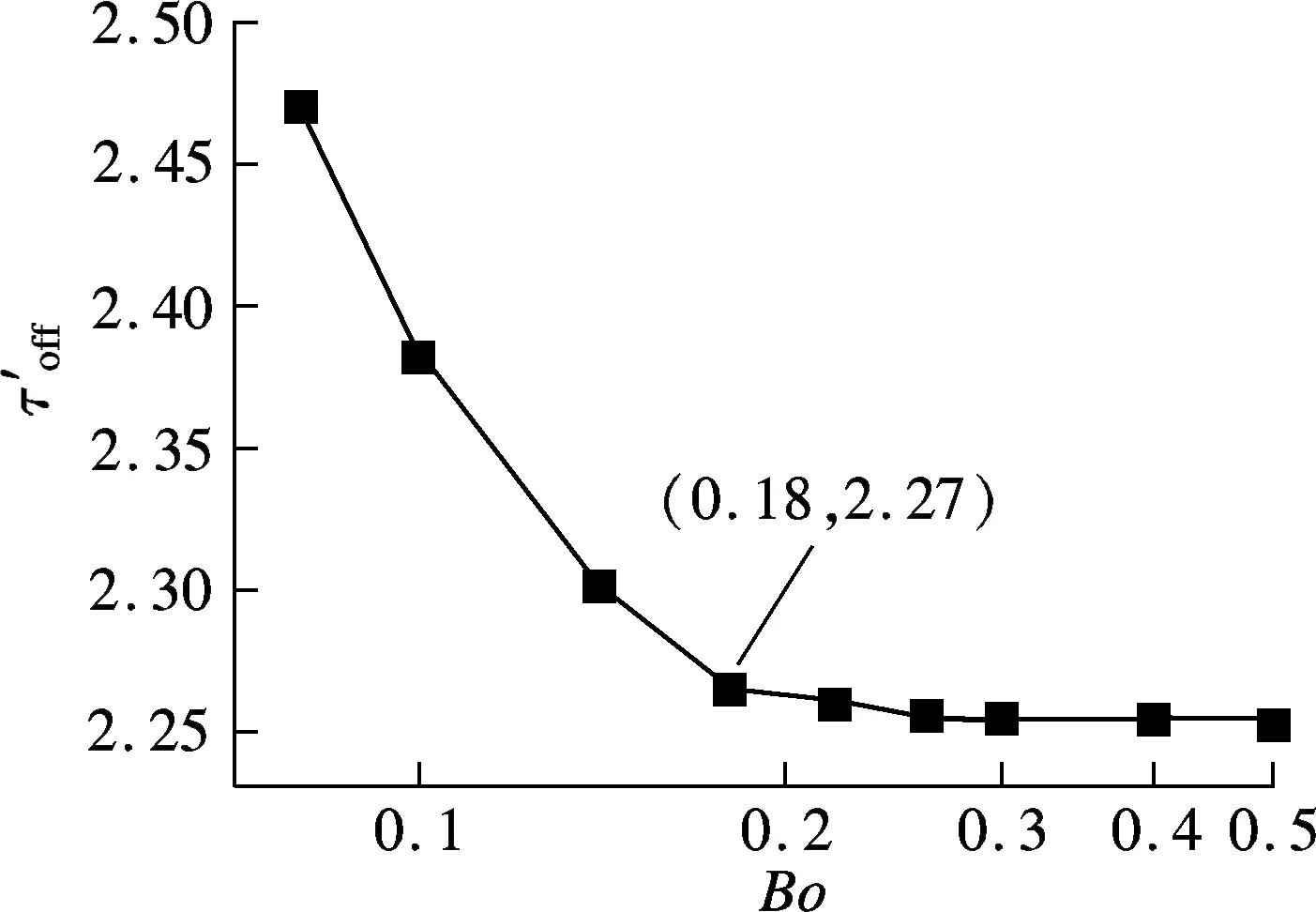
图6 Bond数对断裂时间的影响

4 结论

1) 液滴接触后,液滴间形成液桥并在表面张力作用下快速扩展;随着液桥体积的增大,在液桥与针头间出现颈缩现象.

2) 悬滴与卧滴合并过程存在“合并无断裂”和“合并后断裂”2种流型,当Bo>0.05,出现颈部断裂现象.相对于“合并无断裂”流型,“合并后断裂”流型下颈部更细,存在高压区,驱使流体流出颈部而断裂.

3) 液滴合并后断裂的无量纲时间随Bond数增大而减小,但当Bo>0.18,无量纲时间逐渐趋向一定值.

References)

[1]Whelpdale D M, List R. The coalescence process in raindrop growth [J].JournalofGeophysicalResearch, 1971, 76(12): 2836-2856.

[2]Leach R N, Stevens F, Langford S C. Dropwise condensation—experiments and simulations of nucleation and growth of water drops in a cooling system [J].Langmiur, 2006, 22(21): 8864-8872.

[3]Eggers J. Coalescence of spheres by surface diffusion [J].PhysicalReviewLetters, 1998, 80(12): 2634-2637.

[4]Christopher G F, Bergstein J, End N B,et al. Coalescence and splitting of confined droplets at microfluids junctions [J].LabonaChip, 2009, 9(8): 1102-1109.

[5]Case S C, Nagel S R. Coalescence of low-viscosity liquids [J].PhysicalReviewLetters, 2008, 100(8): 084503-1-084503-4.

[6]Fezzaa K, Wang Y. Ultrafast X-ray phase-contrast imaging of the initial coalescence phase of two water droplets [J].PhysicalReviewLetters, 2008, 100(10): 104501-1-104501-4.

[7]Eggers J, Lister J R, Stone H A. Coalescence of liquid drops [J].JournalofFluidMechanics, 1999, 401: 293-310.

[8]Thoroddsen S T, Takehara K, Etoh T G. The coalescence speed of a pendent and a sessile drop [J].JournalofFluidMechanics, 2005, 527: 85-114.

[9]Wu M M, Cubaud T, Ho C M. Scaling law in liquid drop coalescence driven by surface tension [J].PhysicsofFluids, 2004, 16(7): L51-L54.

[10]Liao Q, Zhu X, Xing S M, et al. Visualization study on coalescence between pair of water drops on inclined surfaces [J].ExperimentalThermalandFluidScience, 2008, 32(8): 1647-1654.

[11]王四芳,兰忠,彭本利,等.超疏水表面液滴合并诱导弹跳现象分析[J].化工学报,2012,63(S1):17-22. Wang Sifang, Lan Zhong, Peng Benli,et al. Characteristics of droplet coalescence and self-propelling on superhydrophobic surface [J].CIESCJournal, 2012, 63(S1): 17-22. (in Chinese)

[12]Duchemin L, Eggers J, Josserand C. Inviscid coalescence of drops [J].JournalofFluidMechanics, 2003, 487: 167-178.

[13]Menchaca-Rocha A, Martinez-Davalos A, Nunez R,et al. Coalescence of liquid drops by surface tension [J].PhysicalReviewE, 2001, 63(4): 046309-1-046309-5.

[14]Yue P T, Zhou C F, Feng J J. A computational study of the coalescence between a drop and an interface in Newtonian and viscoelastic fluids [J].PhysicsofFluids, 2006, 18: 102102-1-102102-14.

[15]Blanchette F, Bigioni T P. Partial coalescence of drops at liquid interface [J].NaturePhysics, 2006, 2(4): 254-257.

[16]Mohammadi M, Shahhosseini S, Bayat M. Direct numerical simulation of water droplet coalescence in the oil[J].InternationalJournalofHeatandFluidFlow, 2012, 36: 58-71.

[17]Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries [J].JournalofComputationalPhysics, 1981, 39(1): 201-225.

[18]Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension [J].JournalofComputationalPhysics, 1992, 100(2): 335-354.

Coalescence characteristic of pendent and sessile droplets

Shen Chaoqun1,2Chen Yongping1,3Shi Mingheng1,2

(1Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China) (2School of Energy and Environment, Southeast University, Nanjing 210096, China) (3School of Hydraulic, Energy and Power Engineering, Yangzhou University, Yangzhou 225127, China)

A theoretical model of the coalescence process of pendent and sessile droplets via VOF (volume of fluid) method is developed and numerically analyzed to investigate the flow regime evolution and hydrodynamics of droplet coalescence under the gravity in air, particularly the droplet coalescence behaviors under different Bond numbers. The result indicates that, due to the surface tension, a liquid bridge forms and quickly expands when two kinds of droplets contact, and the neck appears and shrinks between the liquid bridge and needle tip. Two coalescence flow patterns, “coalescence with no pinch-off” and “coalescence with pinch-off”, are observed under different Bond numbers. The flow pattern changes from “coalescence with no pinch-off” into “coalescence with pinch-off” when Bond number is approximately 0.05. The dimensionless pinch-off time decreases with the rising Bond number and it turns to be constant if the Bond number is larger than 0.18.

droplet; coalescence; flow pattern; neck pinch-off

2014-08-20. 作者简介: 沈超群(1984—),男,博士生;陈永平(联系人),男,博士,教授,博士生导师,ypchen@seu.edu.cn.

国家自然科学基金资助项目(51222605,11190015)、江苏省杰出青年基金资助项目(BK20130009).

沈超群,陈永平,施明恒.悬滴与卧滴合并行为特性[J].东南大学学报:自然科学版,2015,45(1):74-78.

10.3969/j.issn.1001-0505.2015.01.014

TK124

A

1001-0505(2015)01-0074-05