一种最优锚节点集合上的两重粒子群优化DV-Hop定位算法

2015-05-08曹欲晓徐金宝

传感技术学报 2015年3期

关键词：定位精度种群粒子

曹欲晓,严奎,徐金宝

(1.南京工程学院计算机工程学院,南京 211167;2.南京工程学院工业中心,南京 211167)

一种最优锚节点集合上的两重粒子群优化DV-Hop定位算法

曹欲晓1*,严奎2,徐金宝1

(1.南京工程学院计算机工程学院,南京 211167;2.南京工程学院工业中心,南京 211167)

当前粒子群优化的DV-Hop定位改进算法,网络中所有的锚节点都参与优化,但是一部分到未知节点估算距离误差较大的锚节点会引入大的定位误差。针对这种情况,首先提出了最优锚节点集合的概念;然后在定位过程中,应用离散粒子群算法构造了最优锚节点集合;最后在最优锚节点集合上应用连续粒子群算法对定位结果进行了优化。仿真实验表明,最优锚节点集合上的两重粒子群优化DV-Hop算法比DV-Hop和一次粒子群优化的DV-Hop明显提高了定位精度。

无线传感器网络;节点定位;DV-Hop算法;粒子群算法;锚节点;最优锚节点集合

无线传感器网络WSN(Wireless Sensor Network)由大量部署在监控区域的传感节点组成,用来获取监控区域的相关信息。在WSN的大多数应用中,节点获得的传感数据要和自身的位置信息结合起来才有实际意义,没有位置信息的数据往往毫无用处。因此节点定位是WSN领域中一项非常关键的支撑技术[1]。

WSN的节点定位根据是否需要测量节点间的距离或者角度等信息,分成基于测距的定位方法和无需测距的定位方法[2]两种。基于测距的定位方法精度较高,但是需要额外的硬件设备支持;无需测距的定位方法精度相对要低,但是不需要额外的硬件设备,成本较低。DV-Hop即是无需测距定位方法中最为常用的一种,如何提高DV-Hop算法的定位精度具有重要的理论和实际价值[3]。很多研究者采用了多种方法来提高DV-Hop算法的定位精度。这些方法大致可以分成两类:第1类是采用加权平均或者误差修正的方法提高未知节点的平均跳距估算精度,第2类是应用群体智能算法[4]对DV-Hop定位的结果进行优化。文献[5]根据未知节点接收的多个锚节点的平均跳距和到不同锚节点的跳数,把跳数的倒数作为权值进行加权平均,重新计算未知节点的平均跳距。文献[6]把两个锚节点之间的实际距离和估计距离的误差的倒数作为权值,对锚节点的平均跳距进行加权平均。文献[7]利用锚节点和未知节点实际距离和估计距离的误差来修正每跳平均跳距。上述各种改进算法都是基于无偏估计准则计算的锚节点平均跳距。文献[8-11]则把未知节点的定位抽象成一个优化问题,应用粒子群算法对DV-Hop的定位结果进行了优化,并让全部锚节点参与整个优化过程。

现有的基于粒子群优化的DV-Hop(PSO DV-Hop)改进算法,对未知节点的位置进行优化时均是让所有的锚节点都参与定位优化,但是由文献[6]可知,在进行三边测量定位时,如果某些锚节点的估计距离误差过大,反而会使最终的定位误差增大,所以并不是参加定位的锚节点的数量越多越好,应该在保证锚节点数量大于等于3个的前提下,选择一个最优的锚节点集合进行定位。本文应用两重粒子群算法对DV-Hop定位进行了改进,提出了一种新的DV-Hop改进算法:在三边定位阶段,首先应用离散粒子群算法构造一个到未知节点距离误差最小的最优锚节点集合,接着再应用连续粒子群算法在最优锚节点集合上进行定位优化。仿真结果表明,本文算法在无需额外增加硬件设备的情况下,明显提高了未知节点定位的精度。

1 DV-Hop算法

DV-Hop算法把未知节点的平均每跳距离乘以其到锚节点的跳数,以乘积作为未知节点到锚节点的距离。当获得到达3个或3个以上锚节点的距离时,应用三边测量法或极大似然法求出未知节点的坐标。DV-Hop的定位过程可以分成3个阶段[12]。

第1阶段:计算未知节点到锚节点的最小跳数。通过泛洪广播的方式,网络中的每个节点均可获得到达所有锚节点的最小跳数。

第2阶段:计算未知节点到锚节点的估计距离。每个锚节点根据第1阶段获得的其他锚节点的位置信息分组,利用式(1)计算自身的平均每跳距离。式(1)中,(xi,yi)是锚节点i的坐标,(xj,yj)是锚节点j的坐标,hij是锚节点i到j的跳数。

(1)

锚节点向网络广播自己的平均每跳距离,未知节点接收第1个平均跳距,利用式(2)计算自己到每个锚节点的距离,其中hi是第1阶段获得的到锚节点的跳数。

di=Hopsizei×hi

(2)

第3阶段:计算未知节点坐标。未知节点根据第2阶段计算出的di,利用三边测量法或极大似然法计算自身坐标。

2 粒子群算法[13]

2.1 连续粒子群算法

(3)

(4)

式(4)中:w是惯性因子,c1是个体学习因子,c2是全局学习因子,r1和r2是区间[0,1]上的随机数,PB是粒子的个体极值,GB是粒子群的全局极值。

2.2 离散粒子群算法

连续粒子群算法用来求解连续优化问题,为了解决组合优化问题,在连续粒子群的基础上又提出了离散粒子群算法。二进制粒子群优化算法BPSO[14](Binary Particle Swarm Optimization)属于离散粒子群算法中的一种。BPSO算法的位置矢量由实数空间变成了二进制空间,即粒子在每一维上的取值只能是0或1两个值中的一个,但粒子的速度矢量仍然位于实数空间。BPSO算法的速度矢量更新公式用式(4)表示不变,位置矢量更新改用式(5)表示。

(5)

(6)

3 最优锚节点集合上的两重粒子群优化DV-Hop算法

3.1 最优锚节点集合

设WSN中有m个锚节点,n个未知节点,现要对未知节点A进行定位。若A的定位坐标为(x,y),m个锚节点的坐标分别为(x1,y1)、(x2,y2)、…、(xm,ym),A到m个锚节点的估计距离分别是d1、d2、…、dm,实际距离分别是r1、r2、…、rm,则由两点间的距离公式可得:

(7)

设A到m个锚节点估算距离的误差分别是ε1、ε2、…、εm,则|ri-di|≤εi,把式(7)代入|ri-di|≤εi得,

(8)

求解(x,y),使式(9)取得最小值的解即是与未知节点A的真实坐标最为接近的定位结果。

(9)

式(9)的意义是:(x,y)作为计算出的未知节点A的坐标,如果(x,y)到各锚节点的实际距离ri与估算距离di的误差的平方的和越小,则(x,y)就越接近A的真实坐标,那么定位的结果就越精确。为求得更为精确的(x,y),可以通过使式(9)的值最小来实现。这样就把WSN节点的定位问题转化成了一个优化问题,故可以应用粒子群算法求解。

由文献[6]可知,如果未知节点到某些锚节点的估算距离di的误差过大,反而会降低未知节点定位的精度,因此在定位过程中如果能排除这类di误差过大的锚节点,而是在m个锚节点中选择k个估算距离di误差较小的锚节点参加定位,则能提高定位结果的精度,这样的一组锚节点构成的集合称为最优锚节点集合BANS(Best Anchor Nodes Set)。

3.2 两重粒子群优化的DV-Hop原理

从m个锚节点中选择k个构造一个最优锚节点集合,对网络中任意一个锚节点,或者被选中进入最优锚节点集合,或者不被选中。选择多少个锚节点,选择哪些锚节点才能使锚节点集合最优属于组合优化问题,可以应用离散粒子群算法求解。在构造最优锚节点集合过程中使用的粒子群称为种群1。

构造出最优锚节点集合后,再使用另外一个把粒子对应到了未知节点坐标的粒子群,应用连续粒子群算法对定位结果寻优。在这个过程中使用的粒子群称为种群2。对定位结果的优化即为使适应值函数取得最小值为优化目标,以未知节点的坐标作为粒子的位置矢量,经过多次迭代,可以求得最为接近未知节点真实坐标的定位结果。

因为未知节点到锚节点的距离是由未知节点的平均跳距和它到锚节点的跳数相乘估算得到的,未知节点到哪些锚节点的估计距离误差较小事先无法得知,所以最优锚节点集合的构造只能在求解未知节点坐标(x,y)的过程中,通过使适应值函数取得最小值来动态的构造。这就需要把构造最优锚节点集合的离散粒子群算法和在最优锚节点集合上最优化(x,y)的连续粒子群算法融合成一个整体来求解,这种方法称为两重粒子群优化的DV-Hop算法DBPSO DV-Hop(Double PSO DV-Hop)。

3.3 两重粒子群优化的DV-Hop粒子编码

应用粒子群算法求解优化问题的首要任务是粒子编码。下面首先给出求解最优锚节点集合的离散粒子群编码方案。从m个锚节点中选出k个构成最优锚节点集合,m个锚节点中的任意一个或者是集合中的一个元素,或者不是,只有两种可能,因此可以构造一个m维的二进制空间作为粒子的搜索空间。

应用连续粒子群算法优化DV-Hop的粒子编码,采用文献[8-11]中给出的方案,即每个粒子对应未知节点的一个定位优化结果,粒子的两个位置分量表示未知节点的两个坐标,粒子在二维空间中飞行寻优。

3.4 两重粒子群优化的DV-Hop适应值函数

由式(9)知,通过离散粒子群算法求解出的最优锚节点集合对最终定位结果的优化程度,需要通过di和ri(1≤i≤m)误差的平方和来判定,所以DBPSO DV-Hop算法的离散粒子群和连续粒子群要共用同一个适应值函数,这个函数如式(10)所示。适应值函数的设计思想是参加定位的锚节点的di和ri的误差的平方和的平均值最小。

(10)

式(10)中的XDi(1≤i≤m)是种群1中粒子的位置分量,x和y是种群2中粒子的位置分量,β是未知节点到锚节点跳数的倒数。

3.5 两重粒子群优化的DV-Hop步骤

①初始化种群1、种群2的规模都是Q,确定惯性因子w、学习因子c1和c2的值。

②分别初始化种群1、种群2中每个粒子的位置和速度。种群1粒子的初始位置和速度由式(11)、式(12)给出,m是网络中所有锚节点的个数,T(Q)是(0,1)区间上的一个阈值。

(11)

(12)

种群2的位置和速度由式(13)～式(15)给出。Xmax和Ymax是网络中所有锚节点横坐标和纵坐标的最大值,Vmin和Vmax是粒子速度的最小值和最大值,r(0,1)是区间[0,1]上的随机数,rand()是随机数函数。

(13)

(14)

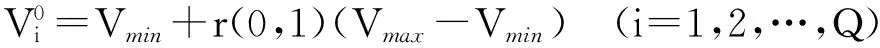
(15)

③计算种群1中粒子和种群2中粒子的笛卡尔积,把笛卡尔积中的每个元素看做一个复合粒子,求出每个复合粒子的个体极值和全部复合粒子的全局极值。

④利用式(5)和式(4)更新种群1中每个粒子的位置和速度,利用式(3)和式(4)更新种群2中每个粒子的位置和速度。

⑤重复步骤③、步骤④,直到完成规定的迭代次数。此时复合粒子的全局极值就是优化后的待定位节点的坐标。

4 仿真结果及分析

4.1 3种算法使用的锚节点比较

由3.1知,对同一个未知节点定位,使用的锚节点不同会导致定位的精度有差别。DBPSO DV-Hop算法的核心思想是在所有锚节点中选出一个能使定位结果误差最小的最优锚节点集合。下面给出锚节点比例为15%时,DV-Hop、PSO DV-Hop、DBPSO DV-Hop 3种算法定位阶段所使用的锚节点的数量、未知节点到锚节点估算距离和实际距离误差的平均值、平均定位误差的比较。

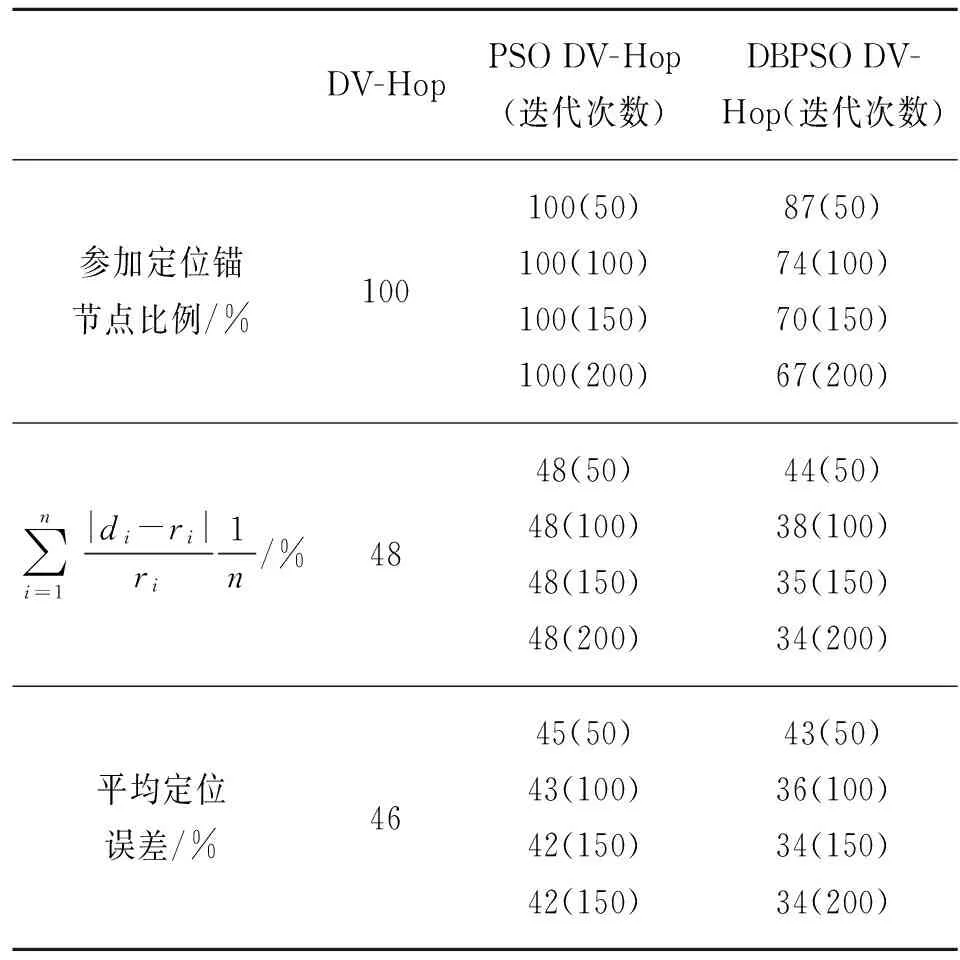
表1 3种定位算法使用的锚节点比较

从表1还可以看出DBPSO DV-Hop算法经过多次迭代,选出的最优锚节点集合中的锚节点估计距离和实际距离的误差较小,使用最优锚节点集合进行优化,定位结果的平均误差也较小。

4.2 3种算法定位结果比较

(16)

为了验证本文提出的DBPSO DV-Hop算法的性能,应用MATLAB软件对DV-Hop、PSO DV-Hop、DBPSO DV-Hop 3种算法进行仿真。仿真环境设为:WSN分布在一个100 m×100 m的正方形区域中,随机生成锚节点和未知节点的坐标,节点的通信半径是50 m。种群1和种群2的规模均是20,惯性因子w=0.9,学习因子c1=c2=2,迭代次数为200次。为了减少随机误差的干扰,每种算法均运行100次取平均值作为最终的实验结果。

图1给出了在节点总数维持200不变,锚节点比例变化的情况下3种定位算法的平均误差比较结果。由图1可以看出,随着锚节点比例的增大,3种定位方法的平均定位误差都在减小,PSO DV-Hop和DBPSO DV-Hop的减小要快于DV-Hop。PSO DV-Hop比DV-Hop平均提高定位精度11%,DBPSO DV-Hop比DV-Hop平均提高定位精度26%。在锚节点比例从15%～25%的区间内,DBPSO DV-Hop定位精度远高于PSO DV-Hop,但是当锚节点比例超过25%以后,两者的差距反而减小。

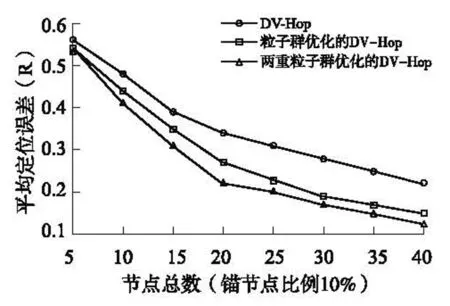
图1 节点总数不变锚节点比例改变的定位误差比较

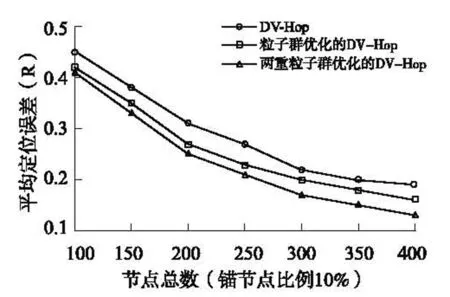
图2 锚节点比例不变节点总数改变的定位误差比较

图2给出了在锚节点比例维持10%不变,节点总数变化的情况下3种定位算法的平均误差比较结果。由图2可以看出,在锚节点比例保持不变的情况下,随着节点总数的增加,锚节点总数也随之增加,3种定位算法的平均误差均呈下降趋势。PSO DV-Hop比DV-Hop平均提高定位精度16%,DBPSO DV-Hop比DV-Hop平均提高定位精度43%。

从以上两种情况下的仿真结果可以看出,DBPSO DV-Hop算法的节点定位精度要明显好于DV-Hop和PSO DV-Hop算法。

5 结语

粒子群算法作为一种性能良好、实现简单的群体智能算法,被很多研究者应用到了WSN的节点定位中,但是目前的粒子群优化DV-Hop算法存在一个共同的问题,即定位寻优时使用了所有可以使用的锚节点,而有些锚节点的测距误差过大,反而会降低最后定位的精度。因此本文的工作在于首先选出一组测距误差较小的锚节点构成最优锚节点集合,只使用最优锚节点参加定位以减小测距误差对定位结果的影响。在所有的锚节点中确定最优者时,由于哪些锚节点的测距误差较小并不知道,所以采用了离散粒子群算法在所有锚节点中组合寻优进行查找。在确定了最优锚节点集合之后,再应用连续粒子群算法最终确定未知节点的坐标。

仿真实验表明,本文提出的DBPSO DV-Hop算法在定位时使用的锚节点在数量上少于DV-Hop和PSO DV-Hop,但在锚节点和未知节点的距离精度上好于上述两种算法。最终的定位结果也表明DBPSO DV-Hop比DV-Hop和PSO DV-Hop在很大程度上减小了定位误差,提高了定位精度。但是DBPSO DV-Hop由于采用了两次粒子群算法,增加了计算的复杂度,并且粒子群算法参数的选取也缺乏相应的理论指导,这是以后需要继续研究改进之处。

[1]Niclescu D,Americ N L. Communication Paradigms for Sensor Network[J]. IEEE Communications Maganize,2005,43(3):116-122.

[2]Bulusu N,Heidemann J,Estrin D. GPS-Less Low Cost Outdoor Localization for Very Small Devices[J]. IEEE Personal Communications Magzine,2000,7(5):28-34.

[3]张震,闫连山,刘江涛,等. 基于DV-Hop的无线传感器网络定位算法研究[J]. 传感技术学报,2011,24(10):1470-1472.

[4]Hackwood S,Beni G. Self-Organization of Sensors for Swarm Intelligence[C]//IEEE International Conference on Robotics and Automation. Piscataway,NJ,USA:IEEE Press,1992:819-829.

[5]刘峰,张翰,杨骥. 一种基于加权处理的无线传感器网络平均跳距离估计算法[J]. 电子与信息学报,2008,30(5):1222-1225.

[6]赵雁航,钱志鸿,尚小航,等. 基于跳距修正粒子群优化的WSN定位算法[J]. 通信学报,2013,34(9):105-114.

[7]石为人,贾传江,梁焕焕. 一种改进的无线传感器网络DV-Hop定位算法[J]. 传感技术学报,2011,24(1):83-87.

[8]张迅,王平,邢建春,等. 传感器网络中改进的粒子群优化定位算法[J]. 计算机科学,2012,39(12):51-54.

[9]蔡绍滨,高振国,潘海为,等. 带有罚函数的无线传感器网络粒子群定位算法[J]. 计算机研究与发展,2012,49(6):1228-1234.

[10]崔焕庆,王英龙,吕家亮,等. 基于随机微粒群算法的分布式节点定位算法[J]. 山东大学学报:理学版,2012,47(9):51-55.

[11]陈星舟,廖明宏,林建华. 基于粒子群优化的无线传感器网络节点定位改进[J]. 计算机应用,2010,30(7):1736-1738.

[12]Niculescu D,Nat h B. DV Based Positioning in Ad Hoc Networks[J]. Journal of Telecommunication Systems,2003,22(14):267-280.

[13]Kennedy J,Eberhart R C. Particle Swarm Optimization[C]//IEEE International Conference on Neural Networks,Ⅳ. Piscataway,NJ,USA:IEEE Service Center,1995:1942-1948.

[14]Kennedy J,Eberhart R C. A Discrete Binary Version of the Particle Swarm Algorithm[C]//The 1997 Conference on System,Cybernetics and Informatics. Piscataway,NJ USA:IEEE Press,1997:4104-4109.

A Kind of Double Particle Swarm Optimization DV-Hop Localization Algorithm Based on Best Anchor Nodes Set

CAOYuxiao1*,YANKui2,XUJinbao1

(1.School of Computer Engineering,Nanjing Institute of Technology,Nanjing 211167,China;2.Industrial Center,Nanjing Institute of Technology,Nanjing 211167,China)

For the improved DV-Hop algorithms based on particle swarm optimization,almost all the anchor nodes in the network are involved in the locating optimization. However,the anchor nodes which have obvious errors between anchor and unknown nodes will lead to big errors of localization. Hence,the concept of best anchor nodes set is proposed. During the process of location,the best anchor nodes set is constructed by employing the discrete particle swarm optimization algorithm. Then the continuous particle swarm optimization algorithm is used to optimize localization for the best anchor nodes set. The simulation results show that the proposed method is effective.

wireless sensor network;node localization;DV-Hop algrothrim;particle swarm optimization algrothrim;anchor node;best anchor nodes set