乳腺MRI图像肿块分割的分段比较与方法研究*

叶希鹏,徐伟栋*,杨 勇,厉力华,杨小丹,张 娟

(1.杭州电子科技大学生命信息与仪器工程学院,杭州 310018;2.浙江省肿瘤医院放射科,杭州 310022)



乳腺MRI图像肿块分割的分段比较与方法研究*

叶希鹏1,徐伟栋1*,杨 勇1,厉力华1,杨小丹1,张 娟2

(1.杭州电子科技大学生命信息与仪器工程学院,杭州 310018;2.浙江省肿瘤医院放射科,杭州 310022)

计算机辅助诊断通过对乳腺磁共振成像(MRI)中肿块区域的自动分割和测量为医生提供定量的诊断依据。对分割过程中不同阶段的多种算法进行实验对比,以此探索更具稳定性和准确性的分割方案:空间模糊C均值(sFCM)聚类算法在肿块的初始定位中具有抗噪声能力和稳定性强的优点,而GVF snake模型在精细分割中对局部轮廓具有较好的收敛性;结合两种算法,并运用MRI序列帧间灰度分布相似、肿块位置/形状相近的原理,最终提高整个序列的分割精度与稳定性。

医学图像处理;乳腺肿块分割;帧间相关性;核磁共振成像;模糊C均值;snake模型

乳腺癌是目前女性疾病中的常见多发病。近年来,由于现代女性不良的生活方式,不断增加的社会压力,晚育或生育后不哺乳等原因,乳腺癌的发病率和死亡率正持续上升。在我国,乳腺癌的发病增长率已达到每年3%～4%。乳腺MRI图像是目前非常重要的乳腺诊断手段。为了提高诊断的准确性和客观性,减轻放射科医生的诊断工作量,利用计算机技术对影像中的病灶进行自动检测与分割是十分必要的。

近几十年来,经过众多国内外研究人员的不懈努力,提出了许多处理各类图像分割的新方法,常用的包括:阈值法、区域生长法、水平集法[1]、几何活动轮廓和一些基于特定理论的算法,包括:人工神经网络、模糊聚类算法、Graph Cuts理论[2-3]等。但由于医学图像本身的特异性与病灶对比度不够明显、边缘模糊等特点,尚未有稳定、普适的分割方法可以应对任意复杂背景下目标的检测与分割需求。在乳腺MRI图像的肿块分割领域,通过反复的比较研究,寻求几种在检测/分割的不同阶段分别专精的算法组成一套稳定性、精度更高的分割方案,比寻找一种从初始定位(粗分割)到精分割都很理想的单一方法更切实可行。

通过分段比较实验,本文发现针对乳腺MRI图像存在灰度值不均匀性和模糊性的特点,空间模糊C均值(spatial FCM)聚类算法[4-5]在肿块的初始定位中具有抗噪能力和稳定性强的特点;而GVF snake模型[6-7]在精细分割中对局部轮廓具有很好的收敛性,通过配合帧间相关性,可以获得一套稳定的乳腺MRI图像分割方法:选取多个不同的聚类数C使用sFCM对乳腺MRI图像进行初始定位,得到粗分割结果;根据得到的初始轮廓,再运用GVF Snake算法对粗分割结果进行精细分割;这样由于不同的参数C就会得到多组分割结果,再利用相邻帧间肿块面积、位置变化平缓、肿块形状相似的特点,将相邻帧间肿块的面积重叠率作为筛选条件,对整个序列的分割结果进行最优化,以提高整个分割结果的精确度[8]。

1 乳腺MRI图像分割算法

1.1 空间FCM分割算法

模糊C均值聚类FCM(Fuzzy C-Means clustering)算法最先由Dunn[9]提出,后经Bezdek[4,10]改进。在医学图像的分割中也得到了广泛的应用[11-12],其在图像分割中的目标就是根据像素点xn的隶属度将图像中n个像素点构成的像素点集X={xk,k=1,2,3,…,n|xk∈Rn}分成C类。FCM聚类算法的目标函数是:

(1)

式中:n为处理的样本总量;c为分类数目;m(1≤m<∞)为控制聚类结果的模糊权重的常数;xk为像素点灰度值;vi为第k类聚类中心;uik是第k个像素点对第i类的隶属度。其中uik应满足如下条件:

(2)

重复计算隶属度函数uik和各聚类中心vi,通过式(3)、式(4)迭代更新:

(3)

(4)

但是FCM算法进行图像分割时仅利用了灰度信息,缺乏对象素的空间信息的利用,只适用于分割低噪声的图像。为此,很多的学者致力于这方面的研究,也提出了很多解决方法[13-15]。

Keh-Shih Chuang[5]等人提出了一种对FCM改进的算法。该算法将空间信息通过空间函数引入到标准FCM的隶属度函数中。该算法记为sFCM(spatial FCM)算法,其空间函数定义为:

(5)

式中:Nk表示以像素点xk为中心的邻域。

与隶属度函数相似,空间函数hik表示像素xk属于第i类的可能性。当一个像素的邻域中的大多数像素都属于同一类时,该类空间函数的值就越大。将空间函数引入隶属度函数的公式如下:

(6)

式中:p和q为两个参数,控制两者所占的比重。

而聚类中心vi的计算方法不变,目标函数变为:

(7)

sFCM算法在分割MRI图像时,某个像素点xk的分类归属不仅仅取决这个像素点xk的灰度值,而是由其邻域其他的像素点和自身的灰度值共同决定。这样,对于一个噪声像素,在计算隶属度时,空间函数可以减少这个噪声点的权重,从而改正由噪声或者伪影造成的误分类。

1.2 GVF Snake算法

Snake主动活动轮廓模型最早由Kass[16]等人在1987年提出。其基本思想是将求取目标边界转化为求取能量最小值的问题。现定义一条闭合曲线υ(s)=[x(s),y(s)](s∈[0,1],s为曲线υ(s)的弧长),以υ(s)为变量的能量函数如下:

(8)

式中:Eint(υ(s))为图像的内部能量项,可以使Snake曲线光滑而且富有弹性;Eext(υ(s))为外部能量项,用来引导Snake曲线去拟合目标的边缘轮廓。

内部能量可以表示为:

(9)

外部能量表达了图像的某些特性,使Snake曲线收敛于图像的特性点,对于灰度图像I(x,y),外部能量可以表示为以下两种:

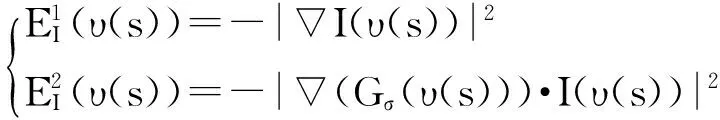
(10)

式中:Gσ(υ(s))是标准方差为σ的二维高斯函数,为梯度算子。

Snake模型在寻找局部的轮廓上具有很好的收敛性,但凹形区域处理能力不足。而改进的算法如梯度矢量流GVF(Grandient Vector Flow)Snake算法在本质上具有更大的捕获范围来处理凹形轮廓[7],使Snake模型收敛。

通过引入一种新的外力场fext=V(x,y)以克服传统Snake模型在处理凹形轮廓上的不足,这种方法叫做梯度矢量流GVF(Grandient Vector Flow)。

现定义GVF场为V(x,y)=(u(x,y),v(x,y)),则有最小化能量函数:

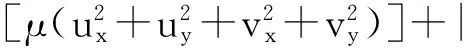
(11)

式中:μ为权衡参数,uxuyvxvy为偏微分,f为梯度矢量场。

当图像变化大时,能量ε主要由f决定;而在缓变区时,f变化缓慢,能量ε由矢量场的偏微分决定。

采用变分法,通过欧拉方程计算,则得到新的能量公式:

(12)

梯度矢量流GVF的优点是:蛇形初始化不需要特别的要求,在图像中搜索的范围较广,可以收缩到凹形图像中。

1.3 基于帧间相关性的分割算法

乳腺MRI肿块图像灰度非均匀,且不同帧间的噪声、伪影不同,不同序列的平均灰度值相差也非常明显,这也造成了使用单一的算法、不变的参数得到的分割结果很不理想。但一个序列的乳腺MRI肿块图像有一个特点:相邻帧间灰度分布相似,肿块组织形态呈平缓渐变。充分利用乳腺MRI肿块图像的这一特点,再结合之前提出的两种算法,本文提出一种参数自适应的基于帧间相关性的乳腺MRI肿块图像分割算法,在对序列MRI图像的分割中有良好的精确度,并可以实现参数自适应,来完成对不同序列MRI图像的自动分割,而不需要人为的干预。算法分为乳腺MRI肿块图像的自动分割和分割结果最优化处理两个部分。

1.3.1 乳腺MRI肿块图像的自动分割

对于一组序列中的每一帧MRI图像,都采用先进行粗分割再进行精细分割的方法。针对乳腺MRI图像灰度值不均匀,有噪声、伪影的特点,选定空间模糊C均值(sFCM)聚类算法作为粗分割方法。sFCM算法虽然不能非常准确的画出肿块的轮廓,但通过对聚类数C值得调节,可以画出肿块的大致轮廓,并具有鲁棒性。

1.3.2 分割结果的最优化处理

乳腺MRI序列图像区别于单帧图像,经实验发现:很难选取一组最优的参数来使整个序列的所有MRI图像都得到理想的分割结果。但可以充分的利用序列图相邻帧间肿块区域的相似性,采用从多组参数的分割结果中寻找最优的分割序列。

本文所用的实验方法中的参数大部分都可以确定,唯独一个sFCM中的聚类数C需要调节。通过n个不同的C值,对序列图像进行sFCM的粗分割,然后使用GVF Snake精细分割,得到n组分割结果,组成矩阵:D=[V1,V2,…,Vm],其中Vi(i=1,2,…,m)为n行列向量,表示第i帧图像在n个参数C值下得到的n个分割结果。乳腺MRI序列图像相邻帧间的肿块面积、形状变化平缓,因此可以使用相邻帧间的重叠面积作为图像质量的判断依据,现定义最优化目标函数:

(13)

式中:a,b为前后相邻帧重叠面积差的权重系数。si为Vi中n个参数C所对应的n个肿块面积,而两个面积相减表示重叠面积差:

sa-sb=Area{sa∪sb}-Area{sa∩sb}

(14)

当每个si选取合适的参数C,使得目标函数达到最小值时,就得到了最优化的分割结果。针对这一问题,可以采用最短路径的数学模型来解决,在这里可以采用经典的Dijkstra算法来解决这个最短路径问题。

2 实验算法分段对比及结果分析

2.1 实验数据

为了验证本文算法的有效性和优越性,将其应用于30例乳腺肿块MRI序列图进行实验,该用例均采集自浙江省肿瘤医院临床用例,图像为dicom格式,图像尺寸均为512 pixel×512 pixel。

对于分割的评价,常用的方法是将算法得到分割结果与专家金标准的分割结果进行像素级的比较,本文采用重叠率作为实验的评价方法,现定义重叠率:

(15)

式中:O为重叠率,C为算法分割结果,R为专家金标准。

2.2 分段对比与算法选定

2.2.1 初始定位方法实验对比

由于乳腺MRI图像的复杂性,目前尚未有一种单一的方法能够应对任意复杂背景下目标的检测与分割需求。因此希望将分割方案分段处理,通过粗分割、精分割两个步骤完成对图像的准确分割。本文对30例序列图像采取了多种算法进行研究,通过粗分割和精细分割两个步骤来完成对图像的分割。其中粗分割方法分别使用大津阈值法,细胞神经网络和sFCM进行比较,通过多组交叉实验,来得出最优的粗分割方法。

表1 3种粗分割方法重叠率对比表 单位:%

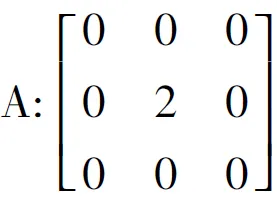
图2为细胞神经网络与sFCM分割结果对比图,图2(a)为使用细胞神经网络作为粗分割方法所得的分割结果,图2(b)为在细胞神经网络粗分割结果后使用GVFSnake得到的精细分割结果,图2(c)为使用sFCM作为粗分割方法所得的分割结果,图2(d)为sFCM粗分割结果后使用GVFSnake得到的精细分割结果。从图中也可以发现,使用细胞神经网络作为粗分割方法也是较为有效的,适用于大多数乳腺MRI图像。但是在分割第3张图像时,把其他的组织误分为目标肿块区域,这个结果导致整个序列的分割精度的下降。不仅如此,在头尾几帧中,由于肿块小且灰度值不明显,使用细胞神经网络做分割,基本得不到良好的分割结果。再将相同的图像使用sFCM进行粗分割,再使用GVFSnake进行精细分割得到的分割结果与图2(a)、图2(b)对比,可以发现,使用sFCM作为粗分割方法,可以更好的将肿块区域与周边的其他干扰组织区分出来,所需要的就是对聚类数C进行适当的调节。

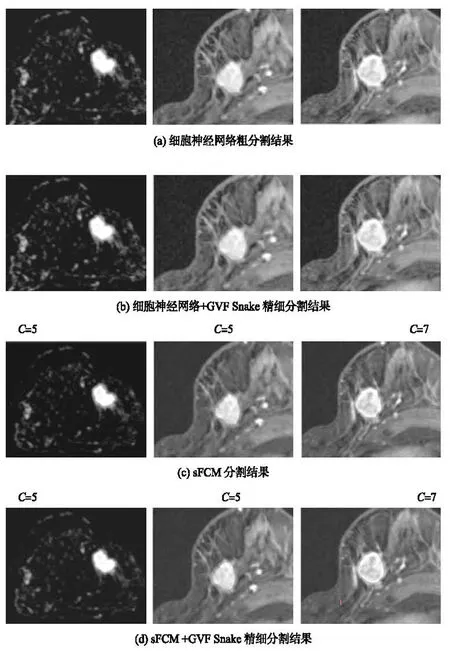
图2 细胞神经网络与sFCM分割结果对比图

2.2.2 精细分割方法实验对比

初始定位方法的目的是将乳腺MRI图像中肿块的大概轮廓分割出来,而精细分割方法则是将肿块的具体轮廓更为准确的提取出来,因此精细分割方法的选定也至关重要。由于精细分割方法受初始轮廓的影响很大,因此精细分割方法的选定不仅仅由精细分割方法本身的优劣所决定,还需考虑所配合的初始定位方法。

接下来对上面提到过的3种初始定位方法结合精细分割方法进行实验,以此来探究更为合适的精细分割方法,其中进行实验的精细分割方法为两种几何轮廓方法。表2为30例乳腺MRI序列图分别经过3种粗分割算法(大津阈值法、sFCM、细胞神经网络)进行分割得到的结果,再分别使用GVFSnake模型和C-V模型进行精细分割得到结果的平均值,共6个均值结果。从表格中可以大致得出3个结论:

①无论使用何种精细分割方法,使用sFCM得到的分割结果远远优于其他两种粗分割方法;

②当粗分割重叠率较低时,如:大津阈值法、细胞神经网络,使用C-V模型所得的精细分割结果要优于GVF Snake模型所得的精细分割结果。这也进一步证明了C-V模型对初始轮廓的敏感度不高,适用于初始轮廓与目标边界偏差较大的情况;

③当粗分割重叠率较高时,如:sFCM,使用GVF Snake模型所得的精细分割结果要优于C-V模型。这也可以说明,GVF Snake在处理局部模糊边界的能力上较C-V模型更强。

表2 2×3交叉实验重叠率对比表(平均值) 单位:%

虽然C-V模型与大津阈值法和神经网络结合所得的分割结果的重叠率要高于GVF Snake,但是由于前面的实验已经充分证明了sFCM的优势,那么这里就需要选择GVF Snake作为精细分割方法。如表3所示,为精细分割结果的重叠率对比表,从表中也可以看出,使用GVF Snake结合sFCM所得的分割结果,不仅其分割结果重叠率的平均值大幅度上升,标准差也有所下降,说明GVF Snake可以使分割结果更加精确地同时,使其稳定性也有所增加,且其均值和稳定性均优于C-V模型。

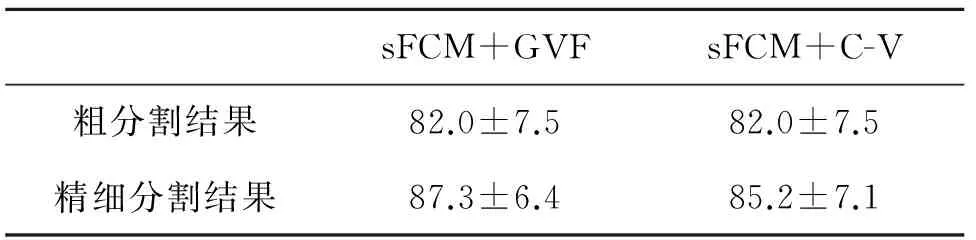
表3 精细分割结果重叠率对比表(均值±标准差) 单位:%

图3 GVF Snake与C-V分割对比图

如图3所示,图3(a)为使用GVF Snake模型的分割结果,图3(b)为使用C-V模型的分割结果,其初始轮廓均为sFCM的初始定位结果。从图中也可以看出,GVF Snake在具有稳定的粗分割结果的情况下,对目标边界具有更高的敏感性,使得对边界的分割更为准确清晰。特别是针对一个序列的前几帧,由于目标边界十分模糊,使用C-V进行精细分割所得的结果就不是特别理想。

2.3 本文算法的实验图像

通过上节中的分段比较实验,可以发现,无论从粗分割结果上看,还是结合精细分割得到的结果来看,sFCM在稳定性方面更优于其他两种算法。

图4为运用本文的算法对乳腺MRI序列图进行分割得到的结果(选取前5帧),其中空间模糊C均值(sFCM)聚类算法设置参数为:模糊权重m=2;GVF Snake模型参数设置为:α=0.3,β=0.3,μ=1(α,β为内部能量Eint中弹性能量和刚性能量的权重系数,μ为内部能量Eint和外部能量Eext的权重系数)。以上为算法中的固定参数,而sFCM中c采用多组取值:c=4,5,6,7。

图4(a)是使用sFCM的粗分割结果;图4(b)是在粗分割的基础上使用GVF Snake算法进行的精细分割,并经过最优化处理,筛选了最优的聚类数C所对应的粗分割和精细分割结果;图4(c)为专家手动分割金标准。可以发现,在精细分割方面,GVF Snake算法对模糊的边界十分敏感,在边缘的特质提取上也很准确,尤其在一个序列的前几帧和后几帧效果更为明显。

图4 乳腺MRI序列图像分割结果图

2.4 分割实验结果分析

2.4.1 粗分割结果分析

本文对30例乳腺MRI图像进行了分割实验,并对算法中粗分割的重叠率对精细分割的影响做了深入探究。分别对这30例乳腺MRI图像使用本文的算法进行分割,和使用手动划分粗分割(所划的粗分割结果较sFCM更精确)后,再使用GVF Snake模型进行精细分割,通过不同的粗分割重叠率来探究粗分割对精细分割的影响。

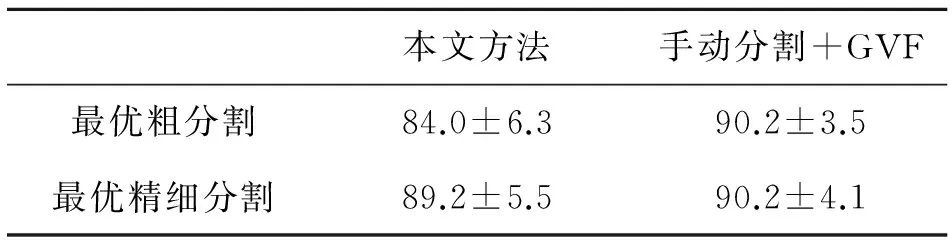
表4 粗分割结果重叠率对比表(均值±标准差) 单位:%

图5是与图4为同一例MRI图像,图5(a)为对这一序列图像进行更高重叠率的手动粗分割,图5(b)为使用GVF Snake进行精细分割。通过图5与图4(b)对比可以发现,手动粗分割相比于sFCM粗分割具有更高的重叠率,但最终的精细分割结果却与本文算法的最优分割结果相差不大。

通过对30例图像进行统计,得到表4,其中包括sFCM、本文方法、手动粗分割、手动粗分割后使用GVF Snake的重叠率。通过纵向上的比较可以发现,经过最优化处理的平均重叠率和标准差达到84.0±6.3,再使用GVF Snake模型精细分割又将分割结果的准确度和稳定性进一步提高。横向上的比较发现,使用手动进行粗分割,平均重叠率和标准差达到90.2±3.5,而进一步的精细分割,准确度和稳定性却没有再提升。通过实验也可以证明,当粗分割的精度达到一定的程度时,再提高粗分割的精度对精细分割的影响就不成正比,影响不大。反而粗分割算法的稳定性更为重要,即粗分割如果能将分割结果定位在目标轮廓的附近,对精细分割的精度和稳定性的提升更为明显。

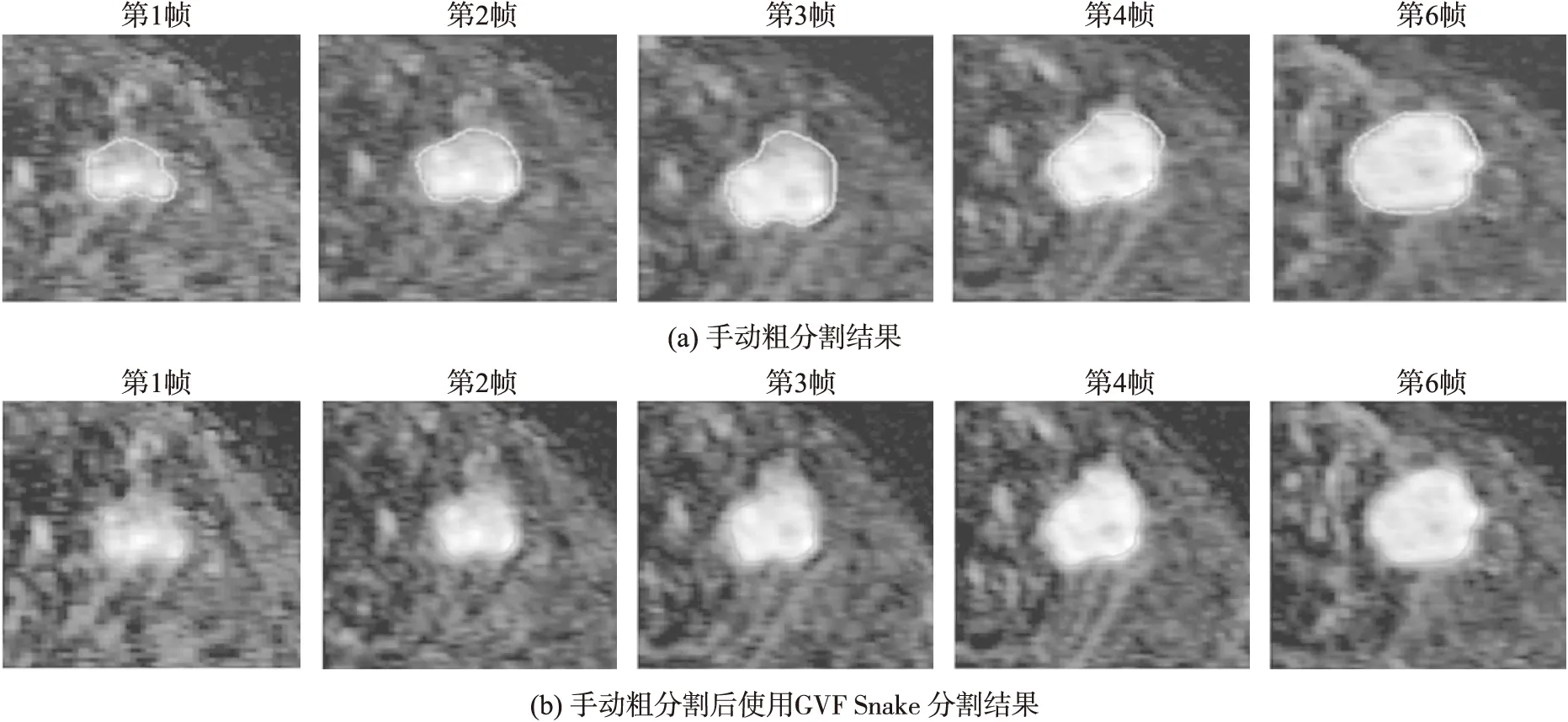
图5 手动粗分割对照实验图

图6是在30例图像的分割结果中随机选取部分序列图像,画出每帧图像经过4种分割方法得到的重叠率的曲线。其中图6(a)为使用本文的sFCM和GVF Snake作为粗精分割方法所得的重叠率曲线图,图6(b)为使用手动粗分割后再使用GVF Snake精细分割得到的重叠率曲线图,图6(c)是本文方法得到的精细分割结果与图6(b)中的精细分割结果的重叠率对比曲线图。可以发现使用算法(sFCM)进行粗分割,当粗分割的重叠率在80%以上时,得到的精细分割结果就与使用手动粗分割得到的精细分割结果重叠率相仿,部分帧使用本文的算法的重叠率还会高出手动分割的结果,这是因为sFCM进行的粗分割的稳定性更好,更能将粗分割轮廓定位在目标轮廓的附近。而当粗分割重叠率小于75%时,粗分割轮廓与目标轮廓相差过大,而本文又是以GVF Snake模型作为精细分割方法,对初始轮廓相对较为敏感,因此对精细分割造成了比较大的影响。

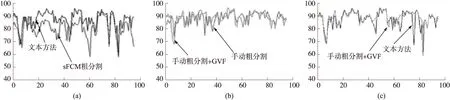
图6 重叠率对比曲线图

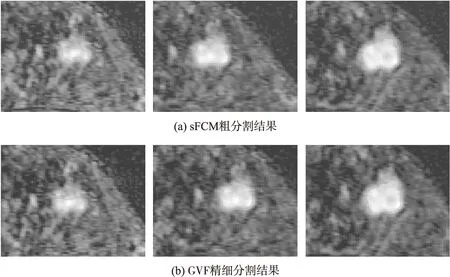
图7 聚类数c=5的部分分割结果

2.4.2 结合帧间相关性信息的最优化结果分析

图7为使用单一的聚类数c=5所得的分割结果,其中图7(a)为sFCM粗分割结果,图7(b)为粗分割结果后使用GVF Snake所得的精细分割结果。图4(b)中的分割结果是结合帧间相关性信息的最优化分割结果,而仅仅采用单一的参数(c=5)对整个序列的图像进行分割,则会得到图7的结果,可以发现,图7得到的结果会与专家金标准相差很大,这是由于聚类数c设置过大,而导致丢失目标信息。通过对30例图像进行帧间相关性信息对重叠率的影响统计,得到了表5,其中本文方法(加入帧间相关性最优化过程)和不使用帧间相关性对分割结果最优化(使用单一的最优聚类数c)进行比较,可以发现,在总体的重叠率上,加入帧间相关性信息,会使得粗分割结果和精细分割结果的重叠率都有明显的提升。

表5 帧间相关性影响重叠率对比表(均值±标准差) 单位:%

从表5中,虽然能够看出帧间相关性的优势,但其均值和标准差的差距仍不明显,因此本课题从30例序列图中随机选择了部分序列,通过对这些序列图有无结合帧间相关性信息的分割结果中肿块面积进行了统计,并分别求出各个序列每帧肿块面积的一阶导数和二阶导数,然后求其一阶导数和二阶导数的标准差,得到表6。一阶导数是肿块面积曲线的导数,表示肿块面积的变化率,而二阶导数表示一阶导数的变化率,因此进一步显示肿块面积是否平稳变化。再求其标准差,通过标准差的大小看一阶导数与二阶导数的变化情况,如果两者标准差大,那么说明帧间肿块面积增加减少不稳定,而两者标准差小,则说明帧间肿块面积变化平缓。从表6中可以看出加入帧间相关性信息得到的分割结果,其一阶导数和二阶导数的标准差更小,其中从二阶导数标准差的数值上看最为明显,因此相邻帧间的肿块面积的变化更为平缓,更加符合实际中肿块的特点。

表6 帧间相关性影响肿块面积变化率对比表(标准差) 单位:%

图8是选取3组序列,将各序列的肿块面积、一阶导数、二阶导数用曲线形式表现出来。图8(a)为加入帧间相关性信息后的分割结果数据曲线,图8(b)为使用单一的聚类数C的分割结果数据曲线,当肿块明显,边界稳定时,是否加入帧间相关性信息的作用不大,但是当边界模糊,特别是在一个序列的头尾几帧时,加入帧间相关性信息就可以使肿块的面积的变化更加稳定,从而使肿块的真实边界被更加精确的分割出来。

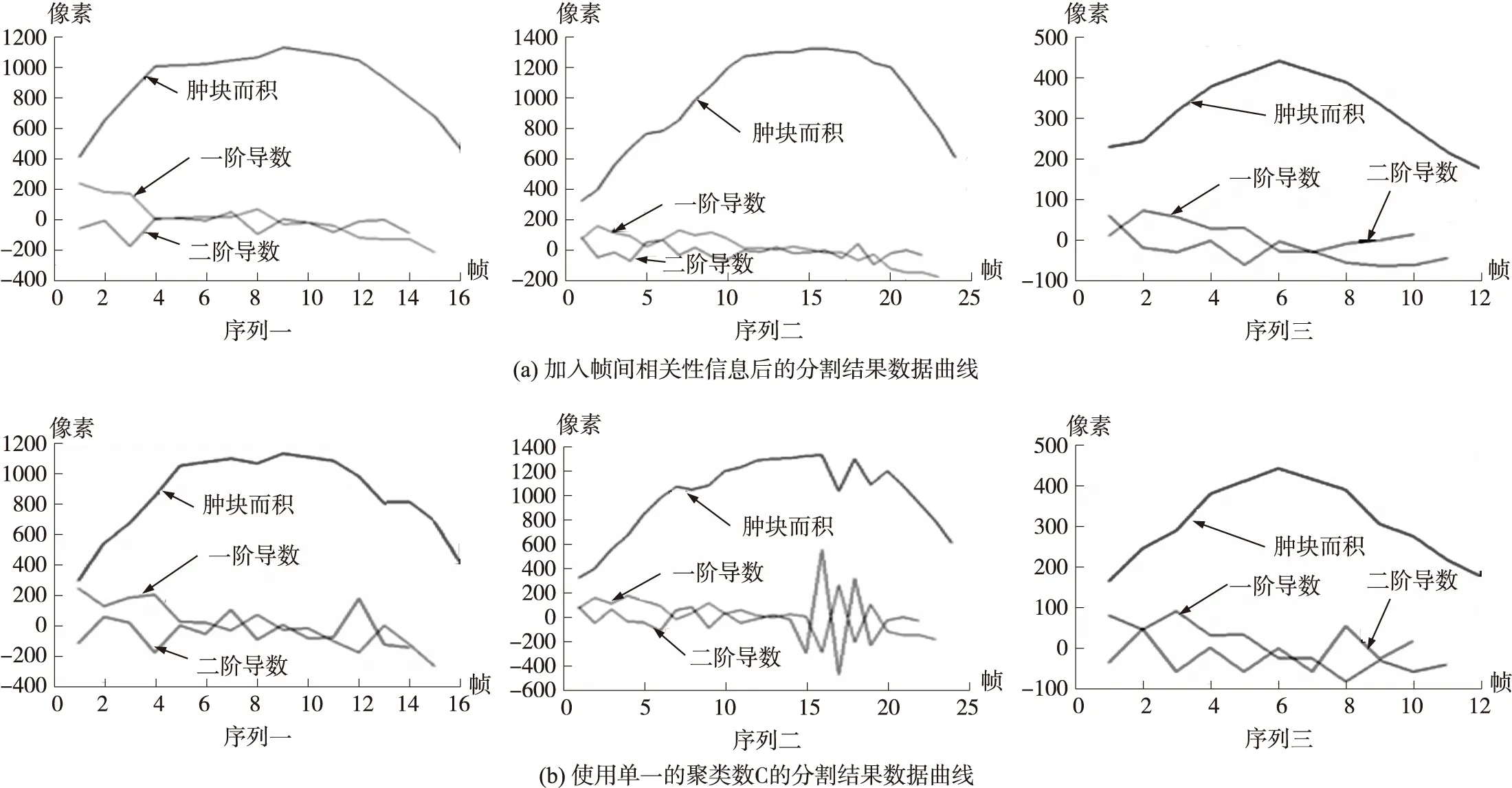
图8 3组序列的帧间相关性对比曲线

3 结语

本文针对乳腺MRI图像的成像特点,以及序列图像帧间相关性(相邻帧间肿块大小形状形似、变化平缓,图像灰度值相近等),提出一种基于帧间相关性的乳腺MRI序列图像的分割方法,分为使用sFCM初始定位,GVF Snake模型进行精细分割,再利用帧间相关性原理对分割结果最优化。实验证明,该方法具有很高的自适应性和较高的精准度,并且对一序列图像完全可以达到全自动分割的操作,无需手动进行。

[1]虞红伟,厉力华,徐伟栋,等. 一种基于水平集的多尺度乳腺肿块分割方法[J]. 仪器仪表学报,2010,31(6):1418-1423.

[2]吴相颖,徐伟栋,厉力华,等. 一种基于Graph Cuts的多尺度乳腺肿块分割方法[J]. 传感器学报,2011,24(10):1379-1384.

[3]朱益苗,徐伟栋,厉力华,等. 基于改进Marching Cubes算法的乳腺MRI肿块三维重建[J]. 传感技术学报,2013,26(4):439-446.

[4]Bezdek J C. A Convergence Theorem for The Fuzzy ISODATA Clustering Algorithm[J]. IEEE PAMI,1980,1(2):1-8.

[5]Keh-Shih Chuang,Hong-Long Tzeng,Sharon Chen,et al. Fuzzy c-Means Clustering with Spatial Information for Image Segmentation[J]. Computerized Medical Imaging and Graphics,30(2006):9-15.

[6]Kass M,Witkin A,Terzopoulos D. Snakes:Active Contour Models[J]. International Journal of Computer Vision,1988,1(4):321-331.

[7]Xu C,Prince J L. Gradient Vector Flow:A New External Force for Snakes[C]//Computer Vision and Pattern Recognition,1997.Proceedings,1997 IEEE Computer Society Conference on.IEEE,1997:66-71.

[8]朱益苗,徐伟栋,刘伟,等. 基于帧间相关性的乳腺MRI肿块分割及重建[J]. 计算机应用,2013,33(A01):204-207.

[9]Dunn J C. A Fuzzy Relative of The ISODATA Process and Its Use in Detecting Compact Well Separated Clusters[J]. Journal of Cybernetics,1973,3(3):32-57.

[10]Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York:Plenum Press,1981.

[11]裴红利,喻罡,邓振生. 基于多尺度连接模型的脑MRI模糊分类[J]. 计算机工程,2010,36(4):174-177.

[12]李志梅,肖德贵. 快速模糊C均值聚类的图像分割方法[J]. 计算机工程与应用,2009,45(12):187-190.

[13]马莉,张勇,朱磊. 一种偏置场环境下的模糊聚类分割算法[J]. 计算机工程与应用,2005,41(22):27-28.

[14]Pham D L,Prince. Adaptive Fuzzy Segmentation of Magnetic Resonance Images[J]. IEEE Transactions on Medical Imaging,1999,18(9):737-752.

[15]Renjie He,Sushmita Datta,Balasrinivasa Rao Sajja. Adaptive with Contextual Constrains for Segmentation of Multi-Spectral MRI[J]. Conf Proc IEEE Eng Med Biol Soc,2004(3):1660-1663.

The Segmentation Research of Breast MRI Masses*

YEXipeng1,XUWeidong1*,YANGYong1,LILihua1,YANGXiaodan1,ZHANGJuan2

(1.College of Life Information Science and Instrument Engineering,Hangzhou Dianzi University,Hangzhou 310018,China;2.Department of Radiology,Zhejiang Cancer Hospital,Hangzhou 310022,China)

CAD(computer-aided diagnosis)could be applied to assist the doctors in the diagnosis of breast cancer,by providing quantitative parameters of breast tumors with the automatic segmentation and measurements of the tumor regions in breast MRI(magnetic resonance imaging)slices. In order to find out a stable and accurate segmentation scheme,a variety of segmentation algorithm of different stages had been carried upon the contrast experiments. sFCM(spatial Fuzzy c-means clustering algorithm)was applied to locate the tumor roughly for its high denosing ability and stability. And then GVF snake model was utilized to segment the tumor accurately for its high convergence of local boundary. Finally,relevant theory of inter-frame images was used to improve the segmentation accuracy of the whole MRI sequence,since the gray distribution and the positions of the tumors are always very similar in the adjacent slices.

medical image processing;tumor segmentation of breast masses;inter-frame correlation;magnetic resonance Imaging;Fuzzy c-means clustering algorithm;snake model

叶希鹏(1990-),男,硕士研究生,控制工程专业,主要从事医学图像处理,计算机视觉,计算机辅助诊断的研究工作,inally1.13@163.com;

徐伟栋(1977-),男,博士,副教授,生命信息与仪器工程学院生物医学工程系主任,主要从事医学影像的计算机辅助诊断,基于医学数据多源融合的计算机辅助决策等方面的研究。近年来主持与作为核心人员参与了多个国家自然科学基金、浙江省自然科学基金与浙江省科技计划国际合作重大项目的研发,temco@hdu.edu.cn。

项目来源:国家自然科学基金项目(60705016,61001215,61205200);浙江省自然科学基金项目(LY12F03003)

2014-11-09 修改日期:2014-12-29

C:7510

10.3969/j.issn.1004-1699.2015.03.016

R391.4

A

1004-1699(2015)03-0387-09