考虑地形改正的GPS高程拟合研究

史俊莉，李生平

(河南工业职业技术学院，河南 南阳 473000)



考虑地形改正的GPS高程拟合研究

史俊莉，李生平

(河南工业职业技术学院，河南 南阳 473000)

在地形变化较大的地区，地形对GPS高程拟合精度有着不可忽视的影响，而精度与GPS的应用效果有着密切的关系，但是传统的拟合方法往往不尽如人意。高程异常短波分量受到地形的影响最大，需要对其进行精确计算，为此本文提出了一种GPS水准拟合方法。该方法在地形修正的基础上考虑了非格网数据的影响，可以有效地解决短波分量的计算难题。实例表明，本文提出的拟合方法可以有效提高计算精度。

高程异常；GPS；高程拟合；地形改正

一、引 言

GPS定位系统在各个方面都有着广泛的应用，然而其获取的高程只是大地高，是以一个椭球为参考的，并不能直接应用到实际中，需要将其转换为正高或正常高。GPS所测量的高程H84与通常采用的正常高Hr存在一定的差值，即高程异常ζ。求取高程异常ξ最常见的是数学模型法。在平原地区，由于地形变化不大，使用数值逼近法获得的高程转换精度较高，但是在丘陵或山区等地形变化较大的区域，拟合的效果往往不尽如人意。本文对地区起伏对高程异常计算的影响原理进行分析，提出一种GPS水准工程拟合方法，该方法在考虑地形修正的基础上，将非格网数据的影响也进行了分析，以提高地形起伏造成的高程异常短波分量的计算精度。

二、考虑地势变化的高程异常计算分析

根据测量学理论中有关概念可以分析得到，高程异常ξ由3部分组成，即

ξ=ξGM+ξΔg+ξT

(1)

式中，ξGM、ξΔg和ξT分别代表着长波、中波和短波3个分量。其中，ξGM为似大地水准面的长波特征，可以由重力场数学模型获取；ξΔg为局部似大地水准面中波特征，通常根据重力异常边值问题计算得来，这一波段的波长在20～100 km之间；ξT描述20 km以下的短波特征，可以根据地形修正计算得到。

将式(1)中的长波分量和中波分量进行合并，可以得到

ξ=ξ0+ξT

(2)

式中，ξ0为中长波分量。一般来讲，短波分量ξT是由地形起伏造成的，因此在地形变化平缓的区域，可以假设不存在地势变化，即ξT这一分量为零。在地形变化突兀的地区，由于无法忽略地势所产生的影响，短波分量ξT就必须考虑进来。

为了较快地求出ξT，可以利用若干个离散点的GPS数据，再加上地形的修正来实现。首先，将地形变化看作是外界噪声，施加在重力场上。定义一个光滑基面作为参考，只要得到了基面两侧的质量影响，就可以计算出地形起伏的影响值(如图1所示)。

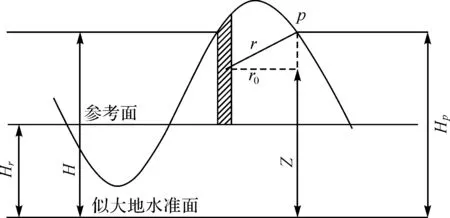
图1 地形在高程异常中的作用效果

图1中，Hr是平均高程面，作为基面；P为测区的一点。由前面分析可知，地形变化会对点P产生扰动，大于或小于基面的地形所产生的扰动可以由三重积分计算出

(3)

式中，G为万有引力常数；ρ为地球平均密度；H为格网点的高程。高程异常短波分量ξT是由地形变化造成的，ξT的值为

(4)

γ为所求点的正常重力值，由下式得到

(5)

(6)

得到计算TC的简化公式为

(7)

三、基于非格网数据的地形改正几何方法

计算点P的高程异常时，由式(7)获得点P周围点对它的引力位，然后对这些引力位求和。如果格网是规则的矩形，由式(7)就可以获得引力位；如果不是规则的形状，则需要进行内插操作，一般是以点P为中心，选取合适的半径以包含若干个网格点。计算时将格网顶面简化为一个平面，矩形格网的计算高程为

(8)

四、地形起伏在GPS高程拟合中的影响

由上面的分析可知，高程异常受到了参考面、格网数据内插方法和格网间距等要素的影响，而这几个因素与地形密切相关，因此地形因素对高程拟合精度有一定的影响。具体分析如下：

1) 测区参考面。基于不同的参考面得到的拟合高程异常数值是不同的，但是不同点之间的高程异常的变化趋势不会随着参考面的不同而变化。在高山区等地形变化很大的区域，一般选择平均参考面，这时的拟合效果要好于其他的参考面。

2) 生成规则格网的内插方法。内插方法对高程异常拟合的结果有着直接的影响，一般选取围绕格网点的小区域内的数据点进行拟合。在遇到一些特殊的地形，如山顶或谷底等，可以借助于已知地势情况，从中获得部分特征点的相关数据，借助于这些信息进行内插。

3) 格网间距。格网间距越小，意味着格网划分的越细，数据信息也就越多，得到的结果往往更好，但是计算耗时更长，因此必须根据地形情况选择合适的格网间距。

五、实例分析

为了验证本文提出的高程异常的计算方法，选取了地形变化较大的区域进行研究，该区域包含11个已知点，如图2所示。

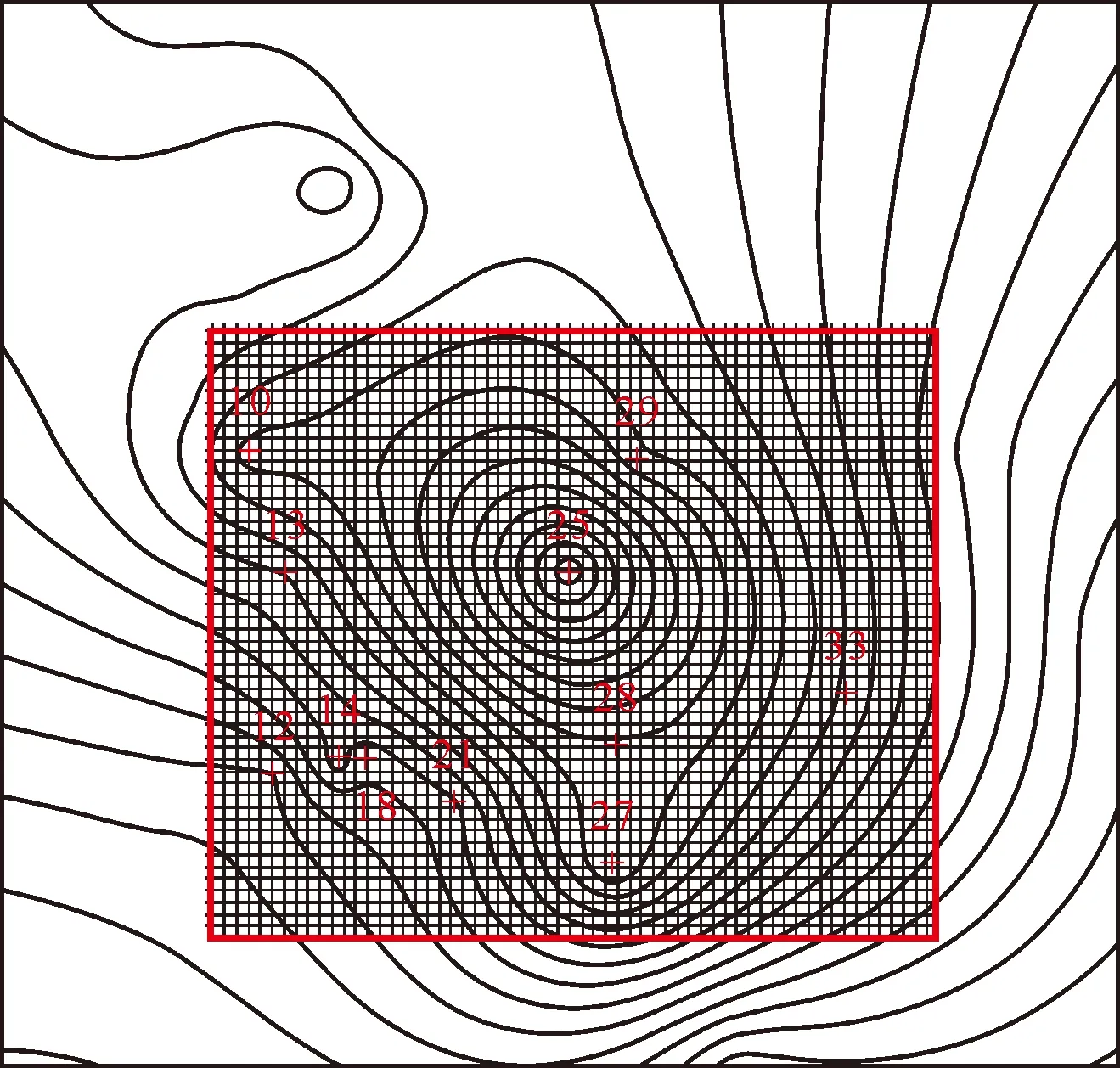
图2 计算区域位置

1.格网间距在地形改正计算结果中的影响分析

利用克里格方法生成规则格网，假设K=10，参考面取为平均高程面，格网间距取不同的值，分别为2000 m×2000 m、1000 m×1000 m、500 m×500 m。以10、14、25、33为例计算得到的结果见表1。

表1 3种不同格网间距地形改正量的结果比较 cm

为了评估精度，借助于移去-恢复法，利用二次曲面函数进行拟合，利用不同的网格间距进行拟合的结果见表2，采用500 m×500 m的格网对计算的精度提高并没有多大帮助，反而是大大增加了计算的工作量，因此1000 m×1000 m是较为合适的格网间距。

表2 格网间距在内外拟合精度中的影响 cm

2.插值方法对计算地形改正的影响

为了评估何种内插方法最适合本地形， 需要对这几种内插方法进行精度评价， 内插精度相应结果见表3。从表中可以看出，克里格法得到的结果比较好，移动二次曲面法也接近于实际结果，这两者的结果与实际数值比较接近。

表3 不同插值方法在拟合精度中的影响比较 cm

六、结束语

本文考虑了地形起伏对高程异常的影响，推导出了扰动的实用计算公式，分析了利用非格网数据进行地形改正的几何方法，并以实例验证了插值方法和格网间距在地形改正中的作用，实例结果表明本文方法有助于提高拟合的精度。

[1] 徐绍铨，张华海，杨志强，等.GPS测量原理及应用[M].武汉: 武汉大学出版社，2002：143-151.

[2] 黄欣，杜国明.利用克里格法对GPS高程拟合的实践[J].测绘与空间地理信息，2011,34(1)：72-74.

[3] 杨丹，奚以成.多面函数法在GPS高程拟合中的应用[J].辽宁省交通高等专科学校学报，2009，11(1)：40-42.

[4] 方亿锋.多项式法在GPS高程异常拟合中的应用[J].测绘与空间地理信息，2010,33(3)：174-175.

[5] 邹辉.GPS高程转换研究[J].山西建筑，2008，34(30)：355-356.

[6] 魏立峰, 何建国.GPS高程拟合似大地水准面的方法[J].地理空间信息，2010，8(4)：72-73.

[7] 蒋平.小区域似大地水准面精华方法的研究[D].西安: 西安科技大学,2011.

[8] 高宁，高彩云，吴良才.GPS高程迭加拟合模型的研究[J].西安科技大学学报，2009，29(3)：339-343.

GPS Height Fitting Research Considering Topographic Correction

SHI Junli，LI Shengping

史俊莉，李生平.考虑地形改正的GPS高程拟合研究[J].测绘通报，2015(7)：66-67.

10.13474/j.cnki.11-2246.2015.0213

2014-07-10

史俊莉(1984—)，女，硕士，研究方向为精密测量与GPS定位技术。E-mail：996890831@qq.com

P228.4

：B

：0494-0911(2015)07-0066-02