一种改进的UKF算法在捷联惯导初始对准中的应用

马宏阳，程鹏飞，王潜心

(1.中国测绘科学研究院，北京 100830； 2.国家测绘产品质量检验测试中心，北京 100830)



一种改进的UKF算法在捷联惯导初始对准中的应用

马宏阳1，程鹏飞2，王潜心1

(1.中国测绘科学研究院，北京 100830； 2.国家测绘产品质量检验测试中心，北京 100830)

Unscented卡尔曼滤波具有精度高、稳定性好、实用性强等特点，因此UKF算法逐渐成为处理非线性滤波问题的有效方法和导航系统中数据处理与信息融合技术的研究热点。但是UKF具有计算量大、效率低等缺点，因此限制了UKF在实时导航中的应用。针对这一缺点，本文提出了一种改进的UKF算法，该算法可以减少UT变换中Sigma点的计算数量，从而提高运算效率；推导了改进的算法公式，给出了适合该算法的初始对准非线性模型，并分析了其精度，用实测数据进行了验证。结果显示，改进的UKF算法性能与传统UKF相当，但效率提升了40%左右。

UT变换；UKF；初始对准；捷联惯导；Sigma点

一、引 言

初始对准是惯性导航的关键技术之一，对准中常提到两个指标：对准精度和对准速度[1]。由于初始对准误差方程是非线性的，因此在小失准角情况下，利用扩展卡尔曼滤波(EKF)通常可以得到比传统卡尔曼滤波更优的估值。但是EKF的本质是非线性方程线性化，这样舍弃了非线性的高阶项，导致滤波结果为次优，在某些情况下甚至会发散，影响系统的正常工作[2]。20世纪90年代中期以来，人们逐渐抛弃了传统的非线性模型Taylor展开近似的方法，采用非线性变换思想，产生了无迹卡尔曼滤波(UKF)[3]。

UKF以UT变换为基础，采用卡尔曼滤波框架，具体采样形式为确定性采样，而非PF的随机采样，最常用的是(2n+1)个Sigma点的对称采样[4]。该滤波直接利用非线性模型，避免引入线性化误差，并且采用的是确定性采样，避免了PF的粒子点退化问题，提高了滤波精度。但是由于Sigma点计算量降低了算法的效率，限制了其在实时导航中的应用。

针对UKF算法计算复杂的问题，本文提出一种改进的UKF算法，该算法可以减少Sigma点计算量，从而提高算法效率。本文推导了改进算法中核心的UT变换公式，给出了适合该算法的初始对准误差状态方程并分析其精度，用实测数据对其进行验证，试验结果表明，改进的UKF算法性能与传统UKF相当，但效率提升了40%左右。

二、一种改进的UKF算法

1.传统UT变换

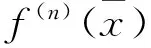
UKF过程可参考文献[7—9]。由UT变换的过程可知，每一次运算都需要(2n+1)个Sigma点经过非线性函数，降低了运算效率。本文给出一种改进的UT变换算法，该算法可以减少Sigma点的计算量，从而提高UKF的效率。

2.改进的UT变换

许多非线性方程是条件线性的。假设非线性方程y=f(x)为条件线性，将状态x分为[aT,bT]T，这样非线性方程可以写成

y=f(x)=ψ(a)+γ(a)·b

(1)

式中，f(x)为任意非线性函数，并且na+nb=n；ψ是a的非线性方程；γ是a的非线性或线性方程。变换后状态的均值和方差为

(2)

定义变量

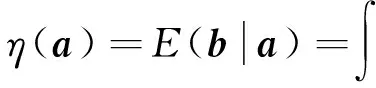
(3)

(4)

方程y的均值由下式计算

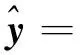
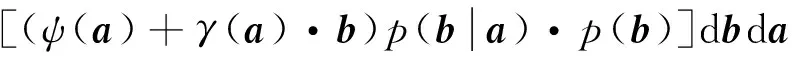
(5)

由式(1)、式(5)可得

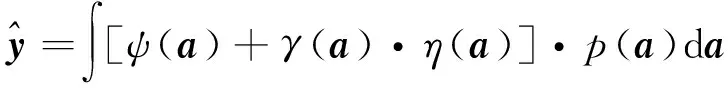
(6)

其中令非线性方程部分为

Φ(a)=ψ(a)+γ(a)·η(a)

(7)

式(6)是通过Φ(a)来计算y的均值，而式(7)可以用前面UT的方法进行估计，计算Sigma点

(8)

权阵Wi也相应地变为

(9)

将选取的状态矢量通过非线性函数得

ξi=Φ(χi)i=0,1,…,2n

(10)

加权近似求解系统统计特性

(11)

由式(2)、式(3)、式(6)、式(7)及式(11)得y的方差Py为

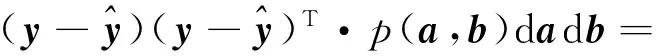
(12)

从上面的过程可以看出，改进的UT算法只需计算(2na+1)个Sigma点，这使计算量大大减小。该UT变换的思想是利用非线性函数中已有的线性化部分来减少整体的计算量，这与分解粒子滤波中仅对线性部分估计其边缘后验概率密度相似。

3.基于改进UT变换的UKF算法过程

(1) 时间更新(预测)

由系统状态方程对各个采样的每一个Sigma点进行非线性变换，得到变换后的Sigma点集为

(13)

对变换后的Sigma点集进行加权处理，从而得到一步预测状态为

(14)

同样的，状态的一步预测方差阵为

(15)

根据一步预测值，再次使用UT变换，产生新的Sigma点集

(16)

(17)

最后使用加权求和计算得到系统的预测观测值

(18)

(2) 量测更新

计算协方差

(19)

可以得到系统量测变量的方差阵

(20)

滤波增益矩阵为

(21)

(22)

求解状态后验方差阵得

(23)

综合上述时间更新和量测更新，UKF滤波过程如图1所示。

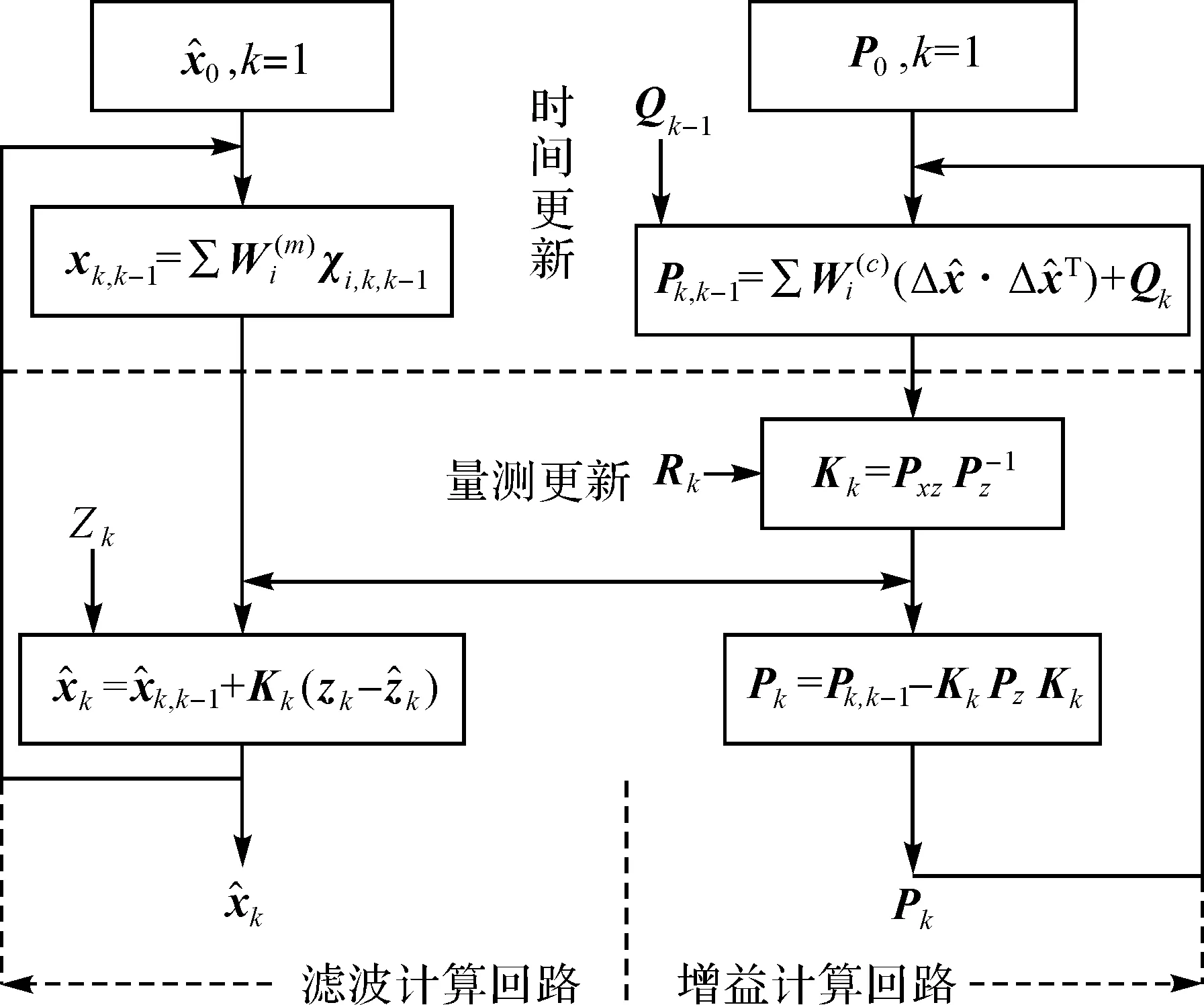
图1 UKF算法流程

三、SINS初始对准非线性模型

1.初始对准原理

在SINS/GNSS组合导航系统中，惯导需要进行初始对准，其主要工作是确定姿态矩阵的初始值，并利用滤波方法将初始失准角估计出来，用于修正姿态矩阵，使系统工作时有正确的初始条件。初始对准的精度会直接影响到系统的精度。因此初始对准是惯性导航的重要阶段，其精度和速度影响着惯导的工作性能，初始对准分为粗对准和精对准过程。

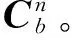
精对准的主要原理是根据粗对准提供的初始姿态矩阵，利用惯性元件输出信息，并用合适的滤波方法，将计算的导航坐标系与真实导航坐标系的失准角估计出来，用来修正姿态矩阵，从而完成初始对准，使计算坐标系与真实坐标系尽可能的重合。

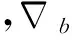
2.捷联惯导初始对准误差模型

捷联惯导初始对准的任务是建立计算坐标系到导航坐标系之间的坐标转换矩阵[5]。通过初始对准误差模型，根据量测值估计出失准角，若不考虑垂直方向的影响，则滤波状态为

x=[δVxδVyφxφyφzΔxΔyεxεyεz]

(24)

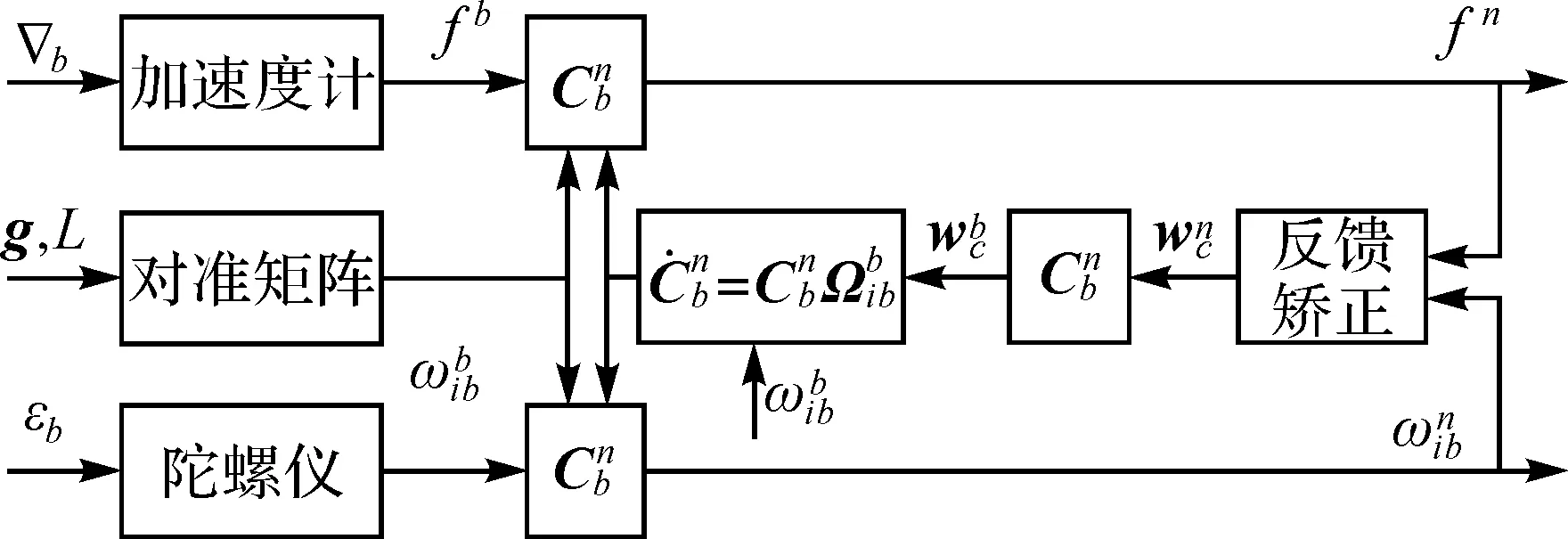
图2 初始对准流程

再根据速度误差方程和姿态误差方程建立的非线性初始对准模型如下[6]

(25)

式中，φx为东向失准角；φy为北向失准角；φz为方位失准角；δVx为东向速度误差；δVy为北向速度误差；L为当地纬度；ωie为地球自转角速度；εx为陀螺东向漂移；εy为陀螺北向漂移；εz为陀螺天向漂移；Δ为加速度计偏置。

为了方便计算，将误差模型离散化为

(26)

式中，dt为时间间隔。

可以看出，该误差方程是条件线性的，结合式(1)及式(26)得

a=[δVxδVyφxφyφz]T
b=[Δε]T

(27)

(28)

(29)

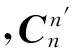
(30)

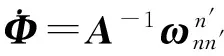
(31)

(32)

考虑一般非线性模型

xk=f(xk-1)+Qk-1

(33)

式中，xk为上述状态模型；f(x)为改进UKF方法非线性状态方程；Q为过程噪声

Q=[qδvxqδvyqφxqφyqφz00000]T

(34)

相应的观测方程为

Y=δV+R

(35)

式中，R=[rxry]T，为观测噪声。

通过上述误差模型可知，利用MUT变换的UKF，每次递归只需计算11个Sigma点，与UT变换每次计算21个Sigma点比起来计算量大大减小。传统的提高运算效率的方法通常是忽略惯导陀螺仪和加速度计的仪器偏差，通常达不到理想的精度。另外一种提高效率的方法是SUKF(simplex UKF)，即利用较少的Sigma点进行计算，但精度也因此受到损失。

由式(1)及式(27)—式(29)可以看出，本文提出的基于MUT变换方法的UKF在11个Sigma点的情况下也可以估计陀螺仪和加速度计的传感器漂移，因为在SINS误差模型中仅仅失准角误差方程和速度误差方程是非线性的，而加速度计偏差和陀螺仪漂移是线性的。由于MUKF也是一种卡尔曼滤波模型，因此它对过程噪声和测量噪声会比较敏感，但是许多健壮噪声矩阵的自适应卡尔曼滤波方法同样也可以应用于MUKF，这些方法本文不再提及。

四、试验与分析

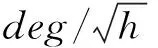
分别用传统的UKF方法与改进的MUKF方法处理数据，速度误差与失准角偏差结果如图3和图4所示。

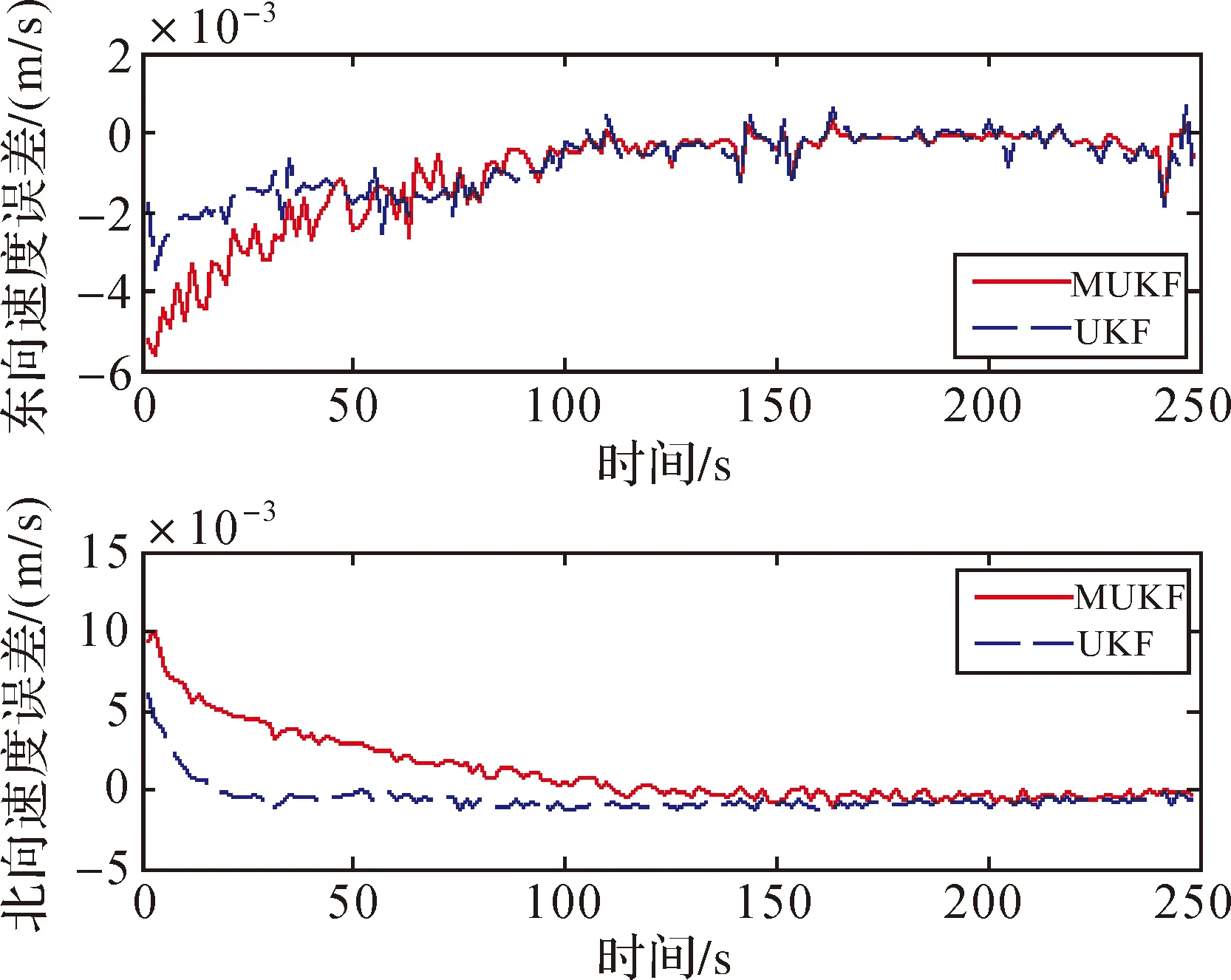
图3 速度误差比较

图3和图4分别是MUKF与UKF速度误差与失准角估计误差比较，从图中可以看出，速度误差估计精度两者相仿，但是MUKF收敛速度较慢。失准角误差估计中，北向失准角误差估计MUKF稍好，东向失准角和方位失准角两者基本相同。本次试验采用的电脑为Inter Core2双核处理器，在计算效率上，MUKF解算时间为3.918 2 s，而UKF解算时间为6.899 4 s，MUKF的解算效率较UKF提高了40%左右，这是因为MUKF在每次非线性递归计算时仅需要计算11个Sigma点，而UKF需要计算21个。因此可以得出，惯性导航初始对准中MUKF与UKF相比性能相似，但MUKF计算效率有了大幅提升。

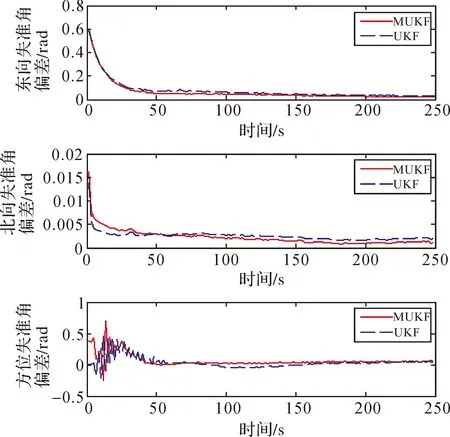
图4 失准角误差比较

五、结束语

本文提出了一种高计算效率的改进UKF方法，并将它应用于捷联惯导初始对准当中。它是基于SINS初始对准误差模型的条件线性，只有速度误差与失准角误差是非线性的。试验结果显示，MUKF与UKF相比有同等的精度，但MUKF计算效率更高，适用于实时导航中。

[1] 陆海勇, 赵伟, 贺荣光, 等.捷联惯导初始对准的UKF改进算法[J].航空兵器, 2009(3): 17-21.

[2] HOVLAND G E, VON HOFF T P, GALLESTEY E A, et al.Nonlinear Estimation Methods for Parameter Tracking in Power Plants[J].Control Engineering Practice, 2005, 13(11): 1341-1345.

[3] JULIER S T, UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE Aerospace and Electronic System, 2004, 92(3): 401-402.

[4] FAUBEL F, KLAKOW D.A Transformation-based Derivation of the Kalman Filter and an Extensive Unscented Transform[C] ∥IEEE/SP 15th Workshop on Statistical Signal Processing.Cardiff: IEEE, 2009: 161-164.

[5] 项冬.高精度机载INS/GPS组合导航关键算法研究[D].北京: 中国测绘科学研究院, 2013.

[6] DMITRIYEV S T, STEMPANOV O A, SHPEL S V.Nonlinear Filtering Methods Application in INS Alignment[J].IEEE Transactions on Aerospace and Electronic System, 1997, 33(1): 260-271.

[7] JULIER S J, UHLMANN J K, DURRANT-WHYTE H F.A New Approach for Filtering Nonlinear Systems[C] ∥Proceeding of the 1995 American Control Conference.Seattle, WA: IEEE, 1995: 1628-1632.

[8] JULIER S J, UHLMANN J K.A New Extension of the Kalman Filter to Nonlinear System[C] ∥The Proceeding of Aero Sense: The 11th International Symposium on Aerospace Defense Sensing.Orlando, FL: Simulation and Controls, 1997: 54-56.

[9] JULIER S T, UHLMANN T K, DURRANT-WHYTE H F.A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators[J].IEEE Transactions on Automatic Control, 2000, 45(3): 477-482.

Application of an Improved UKF Algorithm in SINS Initial Alignment

MA Hongyang，CHENG Pengfei，WANG Qianxin

马宏阳，程鹏飞，王潜心.一种改进的UKF算法在捷联惯导初始对准中的应用[J].测绘通报，2015(7)：18-22.

10.13474/j.cnki.11-2246.2015.0202

2014-03-06

马宏阳(1991—)，男，硕士生，研究方向为GNSS数据处理。E-mail：mahongyangcm@163.com

P228.4

：B

：0494-0911(2015)07-0018-05