基于小波基稀疏信号特征提取的轴承故障诊断

樊 薇， 李 双， 蔡改改， 沈长青， 黄伟国， 朱忠奎

(1.苏州大学城市轨道交通学院， 江苏 苏州 215131； 2.苏州大学机电工程学院， 江苏 苏州 215021)

基于小波基稀疏信号特征提取的轴承故障诊断

樊 薇1， 李 双1， 蔡改改1， 沈长青2， 黄伟国1， 朱忠奎1

(1.苏州大学城市轨道交通学院， 江苏 苏州 215131； 2.苏州大学机电工程学院， 江苏 苏州 215021)

轴承弱故障振动信号中的瞬态成分极易被强背景噪声湮没而无法及时检测，结合稀疏表示原理提出一种基于小波基的稀疏信号特征提取方法，从而实现信号中瞬态特征成分的提取。通过构建原始信号瞬态成分稀疏表示模型，对原始信号采用相关滤波法获取最优小波原子，并构建最优冗余小波基底，实现小波基与信号故障特征的最优匹配；设计二次严格凸函数并运用优化最小(Majorization Minimization,MM)算法求解模型中的目标函数，将信号中的瞬态冲击成分转化为稀疏表示系数，实现强背景噪声下弱特征的有效提取。仿真信号及轴承微弱故障试验验证了该方法能有效地检测和提取强背景噪声下的微弱瞬态成分。

故障诊断； 轴承； 稀疏表示； MM算法； 瞬态成分

引 言

滚动轴承运行过程中损伤点与其他元件接触时产生的周期性冲击是判断轴承局部损伤故障的关键特征信息之一。运用有效的信号处理方法分析振动信号，获得反映旋转机械设备运行状态的瞬态特征信息，是旋转机械故障诊断最为广泛的方法之一[1-2]。然而，在信号采集过程中，由于电机、信号采集系统等设备的干扰以及随机噪声等不可避免因素的影响，实际的振动信号，尤其是微弱故障振动信号往往会被不同程度的噪声所污染，给故障特征提取带来了困难。因此，如何从含强背景噪声的信号中提取出真实的机械振动信号，是故障诊断研究工作的主要任务，也是旋转机械设备故障诊断的关键难题之一。

近年来，基于稀疏表示的特征提取方法在图像处理等领域得到了广泛的应用[3]。Mallet和Zhang首先提出信号在过完备库上分解的思想[4]，通过在过完备库中自适应的选择与信号最相似的原子，并使选择的原子个数尽可能的少，从而得到原始信号非常简洁的表达，即稀疏表示。稀疏表示方法对自然信号用少量的表示系数捕获反映信号特征的主要成分，表达简洁、易于数据存储，已成为图像处理[5]、信号处理[6]、模式识别[7]等领域强有力的工具之一。Selesnick应用稀疏表示的思想，基于正弦基底和分裂增广拉格朗日收缩算法(Split Augmented Lagrangian Shrinkage Algorithm, SALSA)，将非整数周期正弦信号的特征频率成功提取出来[8]；Cai等针对齿轮故障信号的特点，提出基于可调Q因子小波变换和SALSA的信号稀疏分解方法，并成功检测出齿轮振动信号中的瞬态成分[9]。以上研究表明：信号在冗余基底上的稀疏表示研究主要集中在两方面：1)如何构造适合信号特点的冗余基底；2)如何设计优化算法求解稀疏表示问题。

一方面，正弦基底和可调Q因子小波并不适应于机械设备中单边衰减冲击响应波形的提取，而原子库的选取对于信号表达的稀疏度影响十分显著；另一方面SALSA迭代过程中需两次优化目标函数，运算速度慢，影响稀疏表示方法的运算效率。考虑到由Strang G构造出的Laplace小波与单边衰减冲击响应波形最相似[10-11]，而MM算法[12]迭代过程中仅需优化一次目标函数，运算速度较快，本文提出一种新的稀疏信号特征提取方法。首先构建信号瞬态成分稀疏表示模型；再通过相关滤波法选取最优Laplace小波原子，并张成具有不同时移参量的Laplace冗余小波基底，构成稀疏表示基底；然后在选定表示基底的基础上，采用MM算法优化目标函数，求解稀疏表示模型，获得瞬态成分在该基底上的稀疏表示系数，将原始信号中的瞬态冲击响应成分转换成少量非零系数。运用包络解调方法对重构信号进行分析，能较准确地提取轴承故障特征频率。进一步通过不同信噪比下仿真信号与重构信号的相关度验证该方法在强背景噪声下提取弱特征的适应性，并通过提取轴承在弱故障状态下的故障特征频率验证该方法的有效性。

1 信号瞬态成分稀疏表示

1.1 瞬态成分稀疏表示模型及问题

稀疏表示的基本思想是选择冗余基取代传统方法中的正交基，而基底的选择应尽可能的包含被表达信号所含有的信息结构，则从冗余基中选择具有最佳线性组合的若干原子就可以稀疏表示被表达信号，该过程可以表示为逼近过程

(1)

从稀疏角度出发，希望在xr达到最小的情况下得到信号x最稀疏的表示结果。可构造稀疏表示模型如下

(2)

式中α=[α1,α2,…,αK]∈RK×1为稀疏表示向量，D=[d1,d2,…dK]∈RN×K(K>N)为冗余基底，di为D中的原子，零范数(‖·‖0)表示非零元素的个数。采用正则化方法，通过参数λ平衡稀疏性和稀疏表示误差

(3)

式中l0范数优化问题非凸，是NP-hard问题[8]。Candes和Tao[13]证明只要足够稀疏，上式l0范数可以转化为l1范数的非严格凸优化问题

(4)

上述模型中的根本问题在于：1)如何构造适合信号瞬态成分特点的冗余基底D，使信号表示系数稀疏度高；2)如何设计优化算法求解稀疏表示问题，使稀疏表示运算速度快。

1.2 基于相关滤波的冗余基底构造

为解决瞬态特征成分稀疏表示方法在冗余基底选择上的问题，引入相关滤波法，提取出瞬态成分波形特征参数及最优小波原子；再将提取出的小波原子张成具有不同时移参量的最优小波原子库，即冗余基底，作为稀疏表示基底。

针对实际信号中的单边衰减特性成分，选取与冲击响应波形具有类似衰减性质的Laplace小波作为冗余基底D中的原子，冗余基底D为具有不同时移参量的基函数库。Laplace小波为非正交小波，采用复指数形式对信号进行小波变换会增加数据的复杂度和冗余性，考虑到待检测信号为实信号，通常使用Laplace小波实数形式，其解析表达式为

d(t,τ)=ψ(f,ζ,τ,t)=ψγ(t)=

(5)

式中f∈R+表示频率，ζ∈[0,1)⊂R+表示粘滞阻尼比，系数A用来归一化小波函数，Ws表示小波支撑区间。

根据信号稀疏表示的特性，由于冗余基底D是由具有不同时移参量的Laplace小波原子构成，冗余基底中每一个原子与信号中的瞬态冲击响应成分匹配度较高，因此信号中的瞬态成分可以用冗余基底D来稀疏表示，而信号采集过程中的噪声信号与冗余基底D中的原子匹配程度较低，则不能用冗余基底D中的原子稀疏表示，因此该方法能实现强背景噪声下弱故障特征的提取。

1.3MM算法

为提高瞬态特征成分稀疏表示方法的运算速度，引入MM算法，将非严格凸优化问题转换成简单严格凸优化问题，通过优化迭代算法求解目标函数，获得被表达信号在冗余基底D上的稀疏表示系数。

非严格凸优化问题式(4)可以表示为

(6)

MM算法[16]通过求解一系列简单优化问题Gi(α)来逼近原问题的解，即

(7)

(8)

(9)

式中 ‖·‖*表示复共轭转置，Λi=diag(|αi|)为对角阵。保持数据保真项不变，Gi(α)可以表示为

式中 参数λ的选取准则可参考文献[17]。

由此得到瞬态成分稀疏表示模型(4)的快速求解算法，具体步骤如下：

2)按不同时移变化张成最优冗余小波基D(t,τ)。

3)输入原始信号x，参数λ；设定算法停止阈值ε。

4)初始化。令迭代计数变量i=0，初始值α0=D*x。

5)计算对角矩阵Λi。

6)利用代数求导法求解式(10)，得到αi+1。

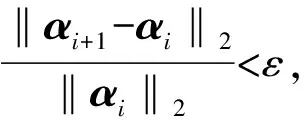
2 仿真分析

为验证Laplace小波基底下瞬态成分稀疏表示的有效性，下面对循环多冲击响应仿真信号进行分析，仿真信号表达式为

式中 时间t∈[0,1]s，f0=200 Hz，ζ0=0.05，τ0=0.1 s，T0=0.2 s，n(t)为高斯白噪声，An为噪声幅值。取An=0.55 m/s2，信噪比为-11.77 dB，用2 000 Hz采样频率对x(t)离散化。取拉格朗日乘子λ=5.04，设定算法停止阈值ε=2.5×e-6。通过Matlab仿真，分析小波基底下的稀疏表示对信号瞬态冲击时间的辨识和对噪声的抑制能力。当信噪比取SNR=-11.77 dB时，仿真信号如图1所示。

图1 仿真信号波形Fig.1 The simulated signal

对图2(c)重构信号进行包络解调分析得到其包络谱图如图3所示，图3表明重构信号的特征频率为5 Hz，与理论值一致。

利用原始信号与重构信号之间的相关系数(Correlation Coefficient,CC)作为重构信号优劣程度的评判标准。相关系数表达式为

(13)

相关系数越接近1，表明重构信号与原始信号的相似程度越大。对图2(c)和图1(a)信号进行相关性计算得重构信号与原始信号的相关系数为0.904，说明该方法不仅能确定含噪信号中冲击响应的发生时刻，且重构信号与原始信号成分非常接近。

为进一步验证该方法对冲击响应发生时刻的辨识能力，表1列出了不同噪声水平下辨识得到的冲击响应时刻，并给出了对应的重构信号与原始信号的相关系数。表中An，SNR分别表示噪声的幅值和对应的信噪比，ti为该方法辨识得到的冲击响应时刻，CC为重构信号与原始信号的相关系数。信噪比定义为SNR=10×lg(Ps/Pn)，其中Ps和Pn分别为信号和噪声的能量。

表1表明，在信噪比达到-13.87 dB时，辨识得到的冲击响应时刻与原始信号的冲击响应时刻误差较大，重构信号与原始信号的相关度也比较低。但随着信噪比的提高，该方法重构的信号与原始信号的相关度也相应提高，信号重构的效果也更好，能较准确地辨识出冲击响应成分的发生时刻，较好的恢复原信号。

图3 重构信号包络谱图Fig.3 The envelope spectrum for the reconstructed signal

3 轴承故障特征信号检测应用

为了检验瞬态成分稀疏表示方法的振动分析应用效果，将该方法应用于轴承外圈、内圈、滚动体的局部故障特征提取。

恒定转速下的轴承外圈、 内圈和滚动体发生故障时，其振动信号表现为周期性的单边衰减瞬态冲击响应信号，可用与该冲击响应成分相匹配的基底稀疏表示，因此可采用本文的方法检测瞬态成分发生时刻，且其时间间隔的均值为轴承各故障下对应的故障特征周期。

表1 不同信噪比下仿真信号的稀疏表示结果

选取圆柱滚子轴承为试验对象，轴承型号为NJ208 (TMB)，轴的旋转速度为1 496 r/min(fr=24.9 Hz)。利用线切割技术分别在轴承外圈、内圈及其中一个滚动体设置了宽度与深度均为0.2 mm的贯通裂痕故障，来模拟轴承局部微弱故障，试验装置如图4所示，该型号轴承的结构参数如表2所示。设置采样频率fs=51.2 kHz，采样点数为5 120，采样时间t=0.1 s。经计算，轴承外圈、内圈和滚动体对应的理论故障特征频率分别为142.8,206.3和132.6 Hz。

图4 试验台外观Fig.4 Rotating machine test rig

3.1 轴承早期外圈故障特征提取

轴承外圈轻微故障时的时域波形如图5(a)所示。从图5(a)中不能得到周期循环多冲击响应成分的发生时刻，因而不能通过时域波形判断出故障类型。

表2 圆柱滚子轴承NJ208 (TMB)的参数

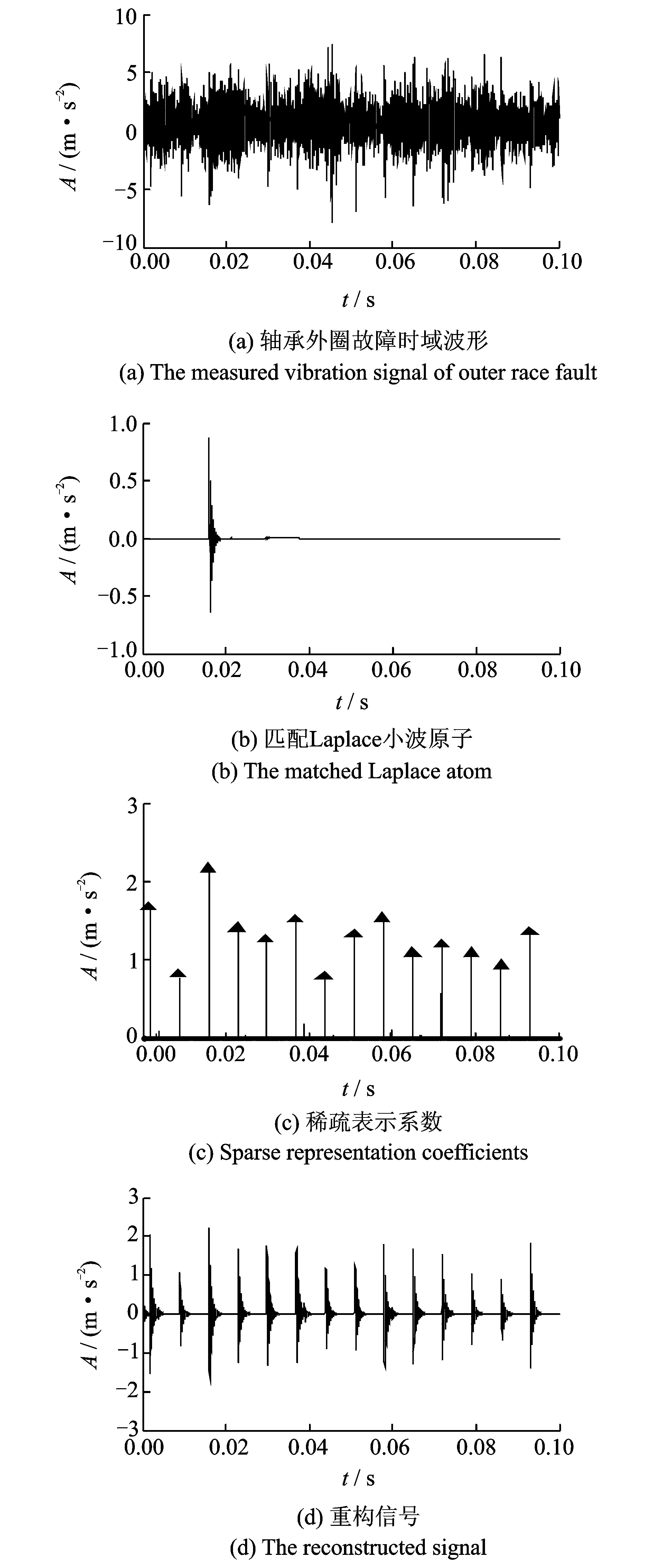
图5 轴承外圈轻微故障振动信号稀疏表示结果Fig.5 The analysis results of outer race fault by using the proposed method

其次，利用MM算法求解该模型(λ=4，ε=1.5×e-5)，得到稀疏表示系数向量如图5(c)所示，从图5(c)中可以直观得到轴承外圈故障时的冲击响应时刻，图5(d)为重构的轴承外圈轻微故障信号。

对图5(d)中重构信号进行包络解调分析得包络谱图如图6所示，图6表明该轴承的故障特征频率为142.9 Hz，与理论值基本一致。

3.2 轴承早期内圈故障特征提取

图7(a)为滚动轴承内圈轻微故障对应的时域波形，不能从时域波形中辨识出瞬态成分发生时刻。

图6 轴承外圈重构信号包络谱图Fig.6 The envelope spectrum for the reconstructed signal of the outer race fault

图7 轴承内圈轻微故障振动信号稀疏表示结果Fig.7 The analysis results of inner race fault by using the proposed method

其次，利用MM算法求解该模型(λ=3.5，ε=1.5×e-5)，图7(c)为稀疏表示系数向量，图7(c)中可直观得到轴承内圈故障时的冲击响应时刻。图7(d)为重构的轴承内圈轻微故障信号。

图7表明该方法能有效识别出冲击响应时刻点和故障周期。对图7(d)中重构信号进行包络解调分析得包络谱图如图8所示，图8表明该轴承的故障特征频率为205.9 Hz，与理论值基本一致。

图8 轴承内圈重构信号包络谱图Fig.8 The envelope spectrum for the reconstructed signal of the inner race fault

3.3 轴承早期滚动体故障特征提取

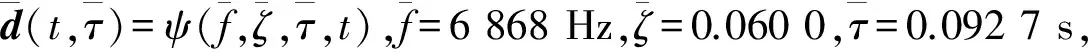
图9 轴承滚动体故障振动信号稀疏表示结果Fig.9 The analysis results of rolling element fault by using the proposed method

其次，利用MM算法求解该模型(λ=6，ε=1.5×e-5)，稀疏表示系数向量如图9(c)所示，从图9(c)中可以直观得到轴承滚动体故障时的冲击响应时刻和故障周期。图9(d)为重构的轴承滚动体故障信号。

对图9(d)中重构信号进行包络解调分析得包络谱图如图10所示，图10表明该轴承的故障特征频率为131.8 Hz，与理论值基本一致。

图10 轴承滚动体重构信号包络谱图Fig.10 The envelope spectrum for the reconstructed signal of the rolling element fault

4 结 论

以信号稀疏表示理论为基础，提出了一种小波基下稀疏信号特征提取方法。首先建立了信号瞬态成分稀疏表示模型并提出了模型中两个关键问题；一方面，采用相关滤波法获得最优小波原子，并张成冗余最优小波基底，解决了基底选择问题；另一方面，设计了二次严格凸函数，并运用MM算法求解模型中的目标函数，解决了方程求解问题。将原始信号中冲击响应成分转换为小波基底下的稀疏表示系数，并利用包络解调分析获得故障特征频率，实现了强噪声背景下弱特征的检测与提取。

仿真信号研究表明稀疏表示方法对冲击响应信号的发生时刻具有很强的辨识性，在一定的信噪比内，该方法能准确定位冲击响应发生时刻，具有较强抑制噪声干扰的能力。将小波基底下信号稀疏表示特征提取方法应用于轴承故障特征提取，试验结果表明，该方法能有效提取轴承轻微故障下外圈、内圈和滚动体振动信号中的冲击响应成分，进而判断轴承故障类型和故障位置。

[1] 陈向民,于德介,罗洁思.基于信号共振稀疏分解的包络解调方法及其在轴承故障诊断中的应用[J].振动工程学报,2012,25(6):628—636.

Chen Xiangmin, Yu Dejie, Luo Jiesi. Envelope demodulation method based on resonance-based sparse signal decomposition and its application in roller bearing fault diagnosis[J]. Journal of Vibration Engineering, 2012,25(6):628—636.

[2] Zhu Zhongkui, Yan Ruqiang, Luo Liheng, et al. Detection of signal transients based on wavelet and statistics for machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2009,23(4):1 076—1 097.

[3] 胡正平,刘文,许成谦,等.局部自适应学习基稀疏约束结合信息优先权选择扩散的迭代图像修复算法研究[J].仪器仪表学报,2010,31(3):600—605.

Hu Zhengping, Liu Wen, Xu Chengqian, et al. Iterative image inpainting using sparse constraint with local adaptive learned dictionary and informational priority selected diffusion[J]. Chinese Journal of Scientific Instrument, 2010,31(3):600—605.

[4] Mallat S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing. 1993,41(12):3 397—3 415.

[5] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006,15(12):3 736—3 745.

[6] Mallat S G. A Wavelet Tour of Signal Processing: the Sparse Way[M]. Academic Press, 2008.

[7] Mei Xue, Ling Haibin. Robust visual tracking and vehicle classification via sparse representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2011,33(11):2 259—2 272.

[8] Selesnick I. Introduction to sparsity in signal processing[EB/OL]. Connexions Web Site, 2012. http://cnx.org/content/m43545/1.3/.

[9] Cai Gaigai, Chen Xuefeng, He Zhengjia. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox[J]. Mechanical Systems and Signal Processing, 2013,41(1):34—53.

[10]Strange G, Nguyen T. Wavelet and Filter Banks[M]. Wellesley-Cambridge Press, 2006.

[11]王诗彬,朱忠奎,王安柱.基于瞬态冲击响应参数辨识的轴承故障特征检测[J].振动工程学报,2010,23(4):445—449.

Wang Shibin, Zhu Zhongkui, Wang Anzhu. Bearing fault feature detection based on parameter identification of transient impulse response[J]. Journal of Vibration Engineering, 2010,23(4):445—449.

[12]Figueiredo M A T, Bioucas-Dias J M, Nowak R D. Majorization-minimization algorithms for wavelet -based image restoration[J]. IEEE Transactions on Image Processing, 2007,16(12):2 980—2 991.

[13]Candes E, Tao T. Near optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006,52(12):5 406—5 425.

[14]Freudinger L C, Lind R, Brenner M J. Correlation filtering of modal dynamics using the Laplace wavelet[A]. Proc. of 16th International Modal Analysis Conference[C]． Santa Barbara, California, 1998:868—877.

[15]Wang Shibin, Huang Weiguo, Zhu Zhongkui. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011,25(4):1 299—1 320.

[16]Hunter D R, Lange K. A tutorial on MM algorithms[J]. The American Statistician, 2004,58(1):30—37.

[17]Chen P Y, Selesnick I W. Translation-invariant shrinkage/thresholding of group sparse signals[J]. Signal Processing, 2014,94:476—489.

Wavelet sparse signal feature extraction method and its application in bearing fault diagnosis

FANWei1,LIShuang1,CAIGai-gai1,SHENChang-qing2,HUANGWei-guo1,ZHUZhong-kui1

(1.School of Urban Rail Transportation, Soochow University, Suzhou 215131, China; 2.School of Mechanical and Electrical Engineering, Soochow University, Suzhou 215021, China)

At early stage of bearing fault，the feature components of the original vibration signal are easy to be submerged in strong background noise and thus are hard to be detected． With sparse representation theory, a novel method for transient sparse representation under wavelet basis is proposed. Sparse representation model is firstly constructed, correlation filtering is applied to obtain optimal wavelet atom, thus the optimal redundant wavelet basis, which can best match the transient features of the signal is realized. A designed strictly convex quadratic function is incorporated into Majorization Minimization (MM) algorithm to solve the objective function. With the proposed method, transients hidden in the noisy signal can be converted into sparse coefficients, thus the transients can be detected sparsely. Both the simulation and a real application of rolling bearings with weak fault demonstrate that the weak transients can be effectively obtained through the proposed method.

fault diagnosis; bearing; sparse representaion; MM algorithm; transients

2014-05-15；

2014-10-16

国家自然科学基金资助项目(51375322,51405321);江苏省自然科学基金资助项目(BK20140339)

TH165.3; TN911.7

A

1004-4523(2015)06-0972-09

10.16385/j.cnki.issn.1004-4523.2015.06.016

樊薇(1990—),女,硕士研究生。电话: 18896512256; E-mail: fanwei.0924@gmail.com

李双(1976—)，男，博士，副教授。电话: 15298898296; E-mail: lishuang@suda.edu.cn