应用精细积分法的结构MBC状态方程求解
2015-05-08李宏男宋建筑
李宏男, 宋建筑
(大连理工大学建设工程学部海岸与近海工程国家重点实验室, 辽宁 大连 116024)
应用精细积分法的结构MBC状态方程求解
李宏男, 宋建筑
(大连理工大学建设工程学部海岸与近海工程国家重点实验室, 辽宁 大连 116024)
基于市场机制控制(Market-based control,MBC)属于分散控制,以往求解状态方程都采用差分类的近似,有时由于计算存在较大误差,不能得到结构真实状态的精确响应。精细积分法以其高精度、无条件稳定等优点被广泛的应用。引入两种精细积分方法,将精细积分的思想运用到基于市场机制(MBC)控制算法的求解中,推导了两种基于MBC控制状态方程的精细递推格式,大大提高了计算的精度及算法的稳定性,并且比较了两种精细积分方法的优缺点。最后通过算例,说明了采用精细积分方法计算MBC控制的必要性及有效性。
基于市场机制控制; 精细积分法; 加法定理; 增量存储
引 言
Clearwater[1]讲述了基于市场竞争体制的控制理论在各领域中的应用,Lynch等[2]率先将MBC(Market-based control)控制算法用于振动工程中。李等[3]总结和探讨了基于市场机制控制理论历程及发展方向,将MBC控制理论应用于安装TLCD的结构振动系统中,建立了多商品市场模型和计算理论等[4-5]。MBC策略的主要思想是将自由市场经济概念引入到系统控制技术中,通过模拟市场行为来完成控制系统中有限能量的Pareto最优分配,使得虚拟市场中各经济个体的效用达到最大化[6-7]。
在结构MBC算法中,如何精确地求解状态方程一直是研究者们关注的热点问题。以往人们往往采用差分类方法近似求解,如高斯积分[8]、龙格-库塔及Simpson积分[9]等方法,这些方法对积分步长很敏感,有时会产生数值病态。钟[10]提出了一种精细时程积分方法,该方法具有很高的精度,可认为达到了计算机上的精确解,并且具有无条件稳定等优点,根据加法定理和增量存储的原则已推导出相应的精细积分递推格式。但该方法需要矩阵求逆,这样会增大计算量并且稳定性会大大降低。改进的精细积分方法[11]避免系统矩阵求逆,易于编程,提高了计算效率。
MBC理论作为一种典型的基于非经典信息的控制方法,控制力的求解只需离散点的状态信息。基于以上精细积分方法的优点,相比于其他全状态反馈的控制算法,结构MBC状态方程采用精细积分方法求解具有在线计算时间短,控制系统反应快等优点。
本文采用精细积分方法推导了MBC控制计算公式的递推格式,求解出结构的状态响应,通过算例验证了各工况下的计算效果。
1 动力方程精细积分方法
在外界干扰和控制力作用下,结构的运动方程可表示为
(1)
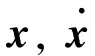
将式(1)运动方程转化为状态方程
(2)

对式(2)采用精细积分下的直接积分法可表示为
(3)
式中
(4)
对于改进的精细积分方法[9],非齐次项的求解不需要矩阵的求逆运算。当非齐次项为多项式函数时,r(tk+1-τ)可表示为
r(tk+1-τ)=f0+τ·f1+τ·f2+…
(5)
将上式代入式(3)得
(6)
由上式可以看出,非齐次项积分重点是如何准确地求解矩阵指数与多项式函数乘积的积分,即
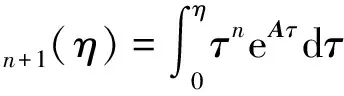
(7)
对式(7)逐个进行分部积分,并采用精细积分的加法定理和增量存储原则求解,得

(8)
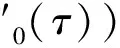
(9)

(10)
这里假定在每一个积分步内对非齐次项做线性近似,谭述君和钟万勰[9]给出的精细积分的递推格式为
Zk+1=φ0(η)Zk+φ1(η)rk+1-φ2(η)r1
(11)
式中
φ0(η)=eAη
(12)
采用精细积分方法[8]计算指数矩阵φ0(η),可达到计算机精度的解。在实时控制中,r(t)为测量得到的等间距信号,故可假定r(t)在(tk,tk+1)线性变化,得
r(t)=rk+r1(t-tk),r1=(rk+1-rk)/η
(13)
钟万勰教授[12]给出了精细积分的递推格式为
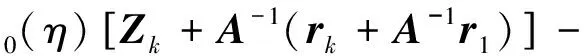
A-1(rk+A-1r1+ηr1)
(14)
将式(14)与(11)比较,改进的精细积分方法递推格式更为简洁,更有利于提高递推效率。
2 控制策略
精细时程积分方法的误差来自幂级数展开式的截断,截去的第1项是在τ5处,此误差已在计算机浮点数表示精度之外,故可得到计算上的精确解。本文将上述两种已有的精细积分方法应用于MBC控制器的求解,可得到结构精确的状态响应。
2.1 基于市场机制的控制(MBC)策略
结构控制系统包括能量源系统和控制装置,在这个虚拟市场中交易的商品是控制能量,自由经济市场包括生产者和消费者。因此,结构控制系统和自由经济体系具有一定的相似性,它们都是在一定的价格准则下实现稀缺资源的合理有效分配。本文采用线性供给-指数需求模型(Linear-supply&Exponential-demandModel,LEM)[13]验证模拟结果,即供给函数
Qs,j=ηj·p
(15)
和需求函数
(16)
当市场达到均衡时
(17)
通过平衡价格p可求得正比与需求能量的控制力
(18)
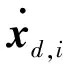
2.2 基于精细积分的MBC控制策略
由精细积分法[12]知,将基本区段η再划分为2M步,M一般取20,即
τ=η/2M
(18)
此时的τ已经非常小了,将φ0(τ),φ1(τ)和φ2(τ)进行有限项的Taylor级数展开,即

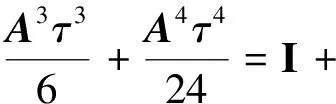
(19)

(20)

(21)
由于τ很小,在τ5截断已满足精度要求。将上式代入到式(8)~(10),再经过M次的合并就可得φ0(η),φ1(η)和φ2(η)的解。以下给出了精细积分方法结合MBC控制得出的状态方程的两种精细递推格式。
(1) 由钟万勰提出的精细积分方法结合本文MBC控制算法,可导出状态方程的精细递推格式为


(22)
式中
(23)

(2) 基于改进精细积分的MBC控制策略,可导出状态方程的精细递推格式为
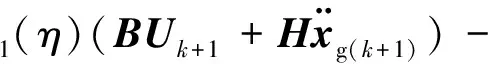

(24)
图2给出了基于改进精细积分的MBC控制流程图。

图1 基于精细积分的MBC控制流程图Fig.1 The precise integration of control flow based on MBC
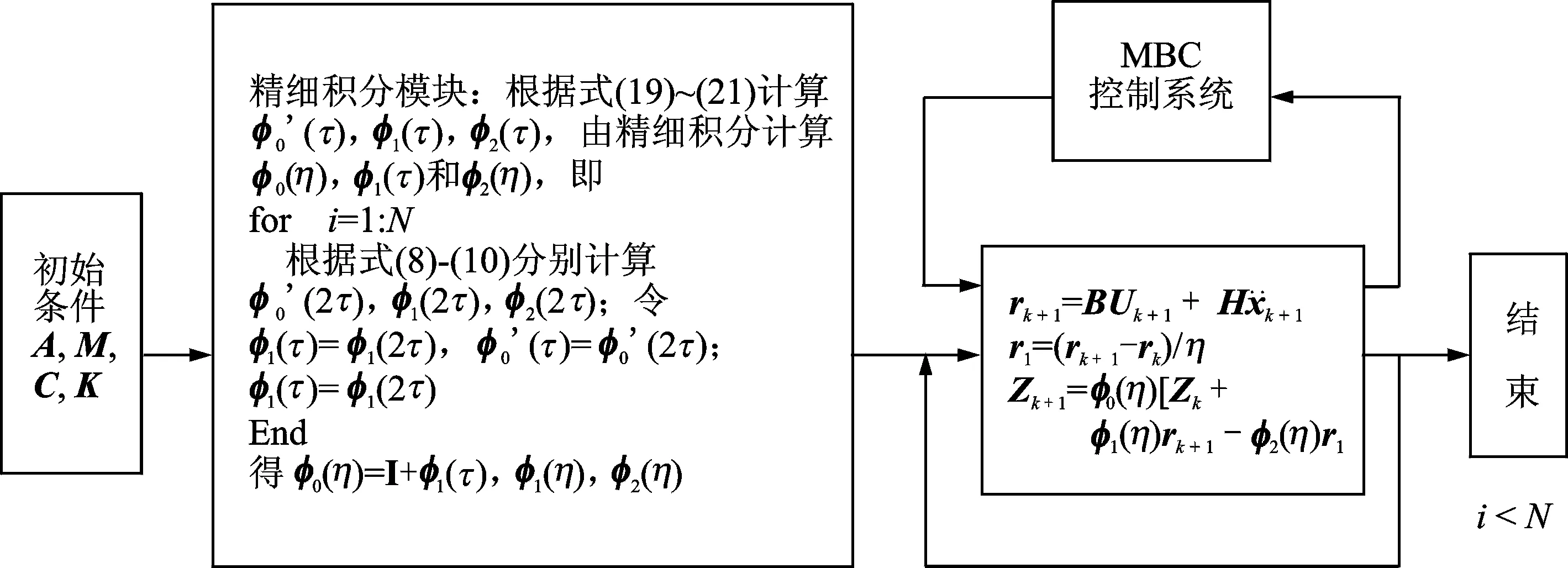
图2 基于改进精细积分的MBC控制流程图Fig.2 Improved precise integration control flow based on MBC
3 数值算例
采用20层剪切型框架结构[14]为算例,主要参数如表1所示;结构阻尼采用Rayleigh阻尼,由前两阶振型阻尼比确定,前两阶阻尼比取0.02。采用MRD作为控制装置对结构进行振动控制,在结构第1~5层每层设置5个MRD,第8~12层各层设置4个,第 15~19层每层设置3个。MRD计算模型采用剪切阀式模型,参数采用文献[13]提供的数据;单个最大出力约1 200kN,可调倍数为50,此处假设阻尼器支撑无限刚。结构的外干扰为ElCentro(N69W,1979)地震波,加速度峰值调整为400gal。
控制器采用线性供给-指数需求模型,其中参数的确定方法根据文献[13]所示求得。每一时刻供需相等时,可以求得该时刻的平衡价格,将价格代入需求函数中,可以得到正比于控制力的能量。
编制相应的MATALB程序对三种工况进行结构分析:
(1)MBC控制下采用龙格-库塔法计算结构的反应(工况1);
(2)MBC控制下采用精细积分的方法计算结构的反应(工况2);
(3)MBC控制下采用改进的精细积分方法计算结构的反应(工况3)。

表1 结构主要参数

表2 各工况在不同积分步长下算法的收敛性及耗时
这里以差分类计算所得的结果作为参照,定义相对误差
式中x0表示采用差分类方法时结构的反应;x表示采用精细积分方法时结构相应的反应。
表2给出了各工况在不同积分步长下控制算法的收敛性及耗时。对差分类而言,步长越小,截断误差越小,但随着步长的减小,在一定范围内需要完成的步数就增加了,不但会引起计算量的增大,而且会导致舍入误差的严重累积。因此,表中给出的最小步长是0.006 s。从表中可以看出,采用精细积分法计算耗时要比差分法耗时小。工况2的收敛步长与工况1的基本一致,但计算时间要比工况1少,工况3耗时最少,精度最高,且收敛步长要比工况1和工况2收敛步长大。可以看出,采用精细积分法计算MBC控制算法具有很大的优势。
图3给出了各工况在不同积分步长下第10层位移峰值响应。从图中可以看出,工况1在步长为0.034 s时发散,工况2在步长为0.04 s时发散,工况3在步长为0.1 s时发散。因此,工况1的收敛步长最小,工况2次之,工况3最大。随着步长的增大,3种工况计算所得的峰值也有较小的增大。说明改进的精细积分法比前面两种工况的收敛步长增大了。
图4无控结构在正弦激励下各方法计算的结构位移响应与解析解的比较。从图中可以看出,精细积分法计算的结构响应接近解析解的结果。而龙格-库塔法计算结构的反应与解析解相差较大。说明精细积分法的准确性较好。

图3 各工况在不同积分步长下第10层位移峰值响应Fig.3 Response of the 10th story in different integration steps

图4 无控结构在正弦激励下各方法计算的结构位移响应与解析解的比较Fig.4 Response of structure displacement of each method and compared with the analytical solution
表3给出了各工况在固定步长为0.006 s时结构第10层反应及相对误差。从表中可以看出,采用精细积分方法计算的结构响应均大于差分类方法计算所得的结构响应,工况2和工况3计算的相对地面位移峰值分别比工况1大7.77%和6.44%;相对误差最大的是绝对加速度,分别比工况1大32.67%和12.93%。

表3 各工况下结构第10层反应及相对误差
图5给出了3种工况下受控结构各层反应峰值,图5(a)为层间相对位移反应峰值的比较,由图可看出,工况2和工况3是采用精细积分计算所得的结构的层间位移峰值,这两种工况计算的结果基本吻合,并且均大于采用差分类计算所得的结果;图5(b)为各层绝对加速度反应峰值,工况3计算的结果最大,工况2次之,工况1最小,说明采用差分类方法计算所得的绝对加速度峰值偏小;图5(c)为各层控制力峰值,由图可看出,在结构上部,工况1计算所得控制力峰值要大于精细积分计算所得峰值;在结构底层,工况1计算所得的控制力峰值小于其它两种工况。

图5 LPM模型下受控结构的反应Fig.5 The response of the controlled structure under LPM model
4 结 论
基于MBC控制采用不同的方法求解所得结果是不同的。由于精细积分法的优点,根据算例已验证了结构MBC算法采用精细积分方法求解状态方程可获得更为准确的结构响应。MBC控制算法是基于离散点的信息,与全状态反馈控制算法相比,具有在线计算时间短等优点。而精细积分法要比差分类的算法计算时间要短,因此,结构MBC状态方程采用精细积分求解显得尤为重要。在以后的研究中,可以将精细积分的思想应用于主动控制器的设计中,这一步工作也正在进行。
[1] Clearwater S. Market-based Control:A Paradigm for Distributed Resource Allocation[M]. World Scientific Publishing,Singapore,1996.
[2] Lynch J P,Law K H.A market-based control solution for semi-active structural control[A]. Computing in Civil and Building Engineering:Proceedings of the Eight International Conference[C].Stanford, CA,USA,Aug 14-16,2000.
[3] 李宏男,李学涛,霍林生.基于市场机制结构控制策略的研究和应用进展[J].世界地震工程,2005, 21(4):1—9.
Li Hongnan,Li Xuetao,Huo Linsheng. Research and application progress of structure control strategy based on Market-Based Control[J]. Earthquake Engineering,2005, 21(4):1—9.
[4] 霍林生,李宏男.基于市场机制的TLCD 半主动控制方案[J].应用力学学报,2005,22(1):71—75.
Huo Linsheng,Li Hongnan. Control law for market-based semi-active timed liquid column dampers [J].Journal of Applied Mechanics,2005,22(1):71—75.
[5] 李宏男,李学涛,霍林生.多维结构振动的改进MBC控制策略[J].振动工程学报,2007,20(4):317—323.
Li Hongnan,Li Xuetao,Huo Linsheng. Advanced market-based control applied in eccentric structure [J]. 2007,20(4):317—323.
[6] Lynch J P, Law K H. Market-based control of linear structural systems[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(10):1 855—1 877.
[7] Lynch J P, Law K H. Energy market-based control of linear civil structures[A]. In:Proceedings of the US-Korea Workshop on Smart Structural Systems[C].Pusan, Korea, August 2002:23—24.
[8] 汪梦甫,周锡元.结构动力方程的更新精细积分方法[J].力学学报,2004,36(2):191—195.
Wang Mengfu,Zhou Xiyuan.Renewal precise time step integration method of structural dynamic analysis[J].Acta Mechanica Sinica,2004,36(2):191—195
[9] 张森文,曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报, 2000,17(1):94—97.
Zhang Senwen,Cao Kaibin.Direct integration of state equation method for dynamic response of structure[J].Chinese Journal of Computational Mechanics,2000,17(1):94—97.
[10]钟万勰.结构动力方程的精细时程积分[J].大连理工大学学报,1994,34(2):131—136.
Zhong Wanxie.On precise time integration method for structural dynamics[J].Journal of Dalian University of Technology,1994,34(2):131—136.
[11]谭述君,钟万勰.非齐次动力方程Duhamel项的精细积分[J].力学学报,2007,39(3):374—381.
Tan Shujun,Zhong Wanxie. Precise integration method for Duhamel terms arising from non-homogenous dynamic systems[J]. Acta Mechanica Sinica,2007,39(3):374—381.
[12]钟万勰.暂态历程的精细计算方法[J].计算结构力学及其应用,1995,12(1):1—6.
Zhong Wanxie. Precise computation for transient analysis[J].Computational Structural Mechanics and Applications,1995,12(1):1—6.
[13]李瀛. 应用MBC策略的建筑结构振动控制[D].大连:大连理工大学, 2007.
Li Ying. Structural vibration control using MBC strategy[D].Dalian:Dalian University of Technology, 2007.
[14]Kurino H,Tagami J,Shimizu K,et al. Switching oil damper with built-in controller for structural control[J]. ASCE,Journal of Structural Engineering,2003,129(7):895—904.
The precise integration of state equation of structures with Market-based control
LIHong-nan,SONGJian-zhu
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)
Market-based control (MBC) belongs to decentralized control. Most of the existing method to solve state equations use differential approximation, which has large errors so that it is hard to obtain the accuracy results. The precise integration has been widely used due to its high accuracy and unconditional stability. In the present study, two precise integration are introduced to MBC computation and the recursive scheme of state equations are derived. This method improve the accuracy and stability, then the advantage as well as disadvantage of the two precise integration have been compared. The necessity and effectiveness of MBC method using precise integration are proved by examples.
MBC strategy; precise computation; addition theorem; incremental storage
2014-01-13;
2015-07-21
国家自然科学基金重大国际合作项目(51261120375);国家重点基础研究计划(973计划)(2011CB013605)和国家自然科学基金创新研究群体资助项目(51121005)
TU311.3; TB535
A
1004-4523(2015)06-0896-06
10.16385/j.cnki.issn.1004-4523.2015.06.006
李宏男(1957—),男,长江学者特聘教授。电话:(0411)84709539;E-mail:hnli@dlut.edu.cn
