典型船体结构拐角区域的应力分布比较研究

高 嵩， 纪永波， 徐 丽， 王大政

(1．交通运输部水运科学研究院， 北京 100088； 2．哈尔滨工业大学(威海)， 山东 威海 264209)

典型船体结构拐角区域的应力分布比较研究

高 嵩1， 纪永波1， 徐 丽2， 王大政2

(1．交通运输部水运科学研究院， 北京 100088； 2．哈尔滨工业大学(威海)， 山东 威海 264209)

加强结构以保证船体的结构强度为主，合理选择结构形式对于船舶安全航行至关重要。为此，采取奇异强度理论与ANSYS数值模拟方法比较分析了4种典型二维结构拐角处的应力分布及其奇异性，进而针对6种船用典型三维结构，分别在拉伸载荷、弯矩载荷及共同作用的工况下，分析并比较了结构拐角处不同方向的应力分布，并明确了有限元分析方法，希望为实际工程应用提供参考。

结构强度 应力分布 奇异性 有限元

1 引言

在船舶工程领域，复杂海况下的交变载荷对于船体结构提出了较高要求，尤以舰船更为突出。对于船体需加强结构处，一般以板和加强筋(板)等焊接而成，以便达到结构强度要求。但这些板架的连接处通常存有锋利的拐角，易发生应力集中现象，产生疲劳裂纹，最终失稳破坏，带来灾难性事故[1]。此外，合理确定舰船加强结构的形式与布置，对于减少船体质量，提高商船的经济效益和舰船的武器储备也至关重要。为此，研究了船体典型结构拐角处应力分布，并通过几种结构形式的比较予以说明。

2 二维拐角应力分布比较

对于二维结构，最早Williams[2]基于弹性理论证明了V型锋利角处应力的奇异性，并给出了结构拐角应力场的精确解；此后，Gross&Mendelson[3]拓展到裂纹应力场，并以应力强度因子(SIF)来描述应力集中程度；Lazzarin[4]则通过大量的有限元计算将SIF与结构尺寸进行关联，并给出计算函数。基于上述研究，徐丽[5]和高嵩[6]分别针对90°和135°二维结构，简化了应力函数及参数的选取，定义了“奇异强度理论”来求解拐角处的应力分布，发现奇异强度as主要取决于非受载板高H和长L，以及受载板高t，并给出关系式as=min(H/2,L/25)[5]和as=min[t(H/h)0.1/6, (2h+L)/8][6]。

表1 几种拐角的结构形式

这里为更好地了解拐角尖端应力分布奇异性，对表1所示的4种形式作了比较研究，通过对不同结构及不同方向上拐角区域的应力分布进行分析，给定工程应用中缓解应力集中及应力分布奇异性的最佳参考方案。

2.1 不同结构形式的应力场

通常应力集中程度取决于焊趾周边的结构尺寸，并与垂直裂纹扩展方向的法向应力场有关。为此，利用ANSYS和“奇异强度理论”分别计算了裂纹扩展方向的垂向应力分布，如图1所示。可以发现，135°拐角处(结构1)的应力集中现象最弱，直角处(结构2)嵌接三角形肘板(结构3)并未明显缓解应力集中，且当直角拐角嵌接矩形肘板处(结构 4)应力集中最为明显，因此考虑实际工程中拐角处应力集中时，建议选择结构1形式。此外利用奇异强度理论计算的拐角处的应力分布与ANSYS的计算结果拟合较好，也说明奇异强度理论的可靠性，可为计算切口应力、SIF及结构疲劳特性分析作参考。

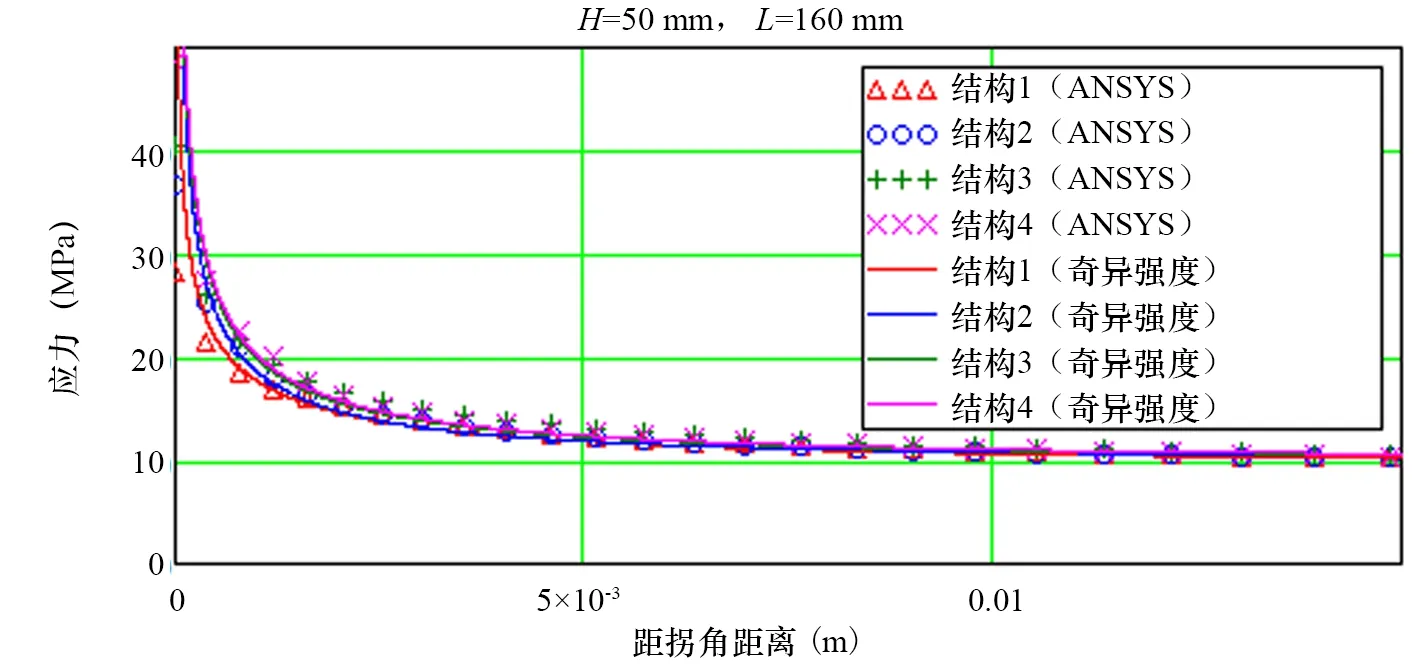
图1 不同二维结构拐角处的应力分布比较

2.2 不同分析方向的应力场

促使裂纹扩展的激力是垂直于裂纹扩展方向上的应力，但裂纹端面结构边缘上的应力也是影响拐角尖端应力奇异性的重要因素，并是适用于线性插值法所需的应力，图2比较了这两个方向的应力场分布。可知边缘方向的应力大于垂直裂纹扩展方向的应力，其不仅证明了拐角尖端应力奇异性的存在，也说明了线性插值法中选取结构边缘方向应力的相对安全性。

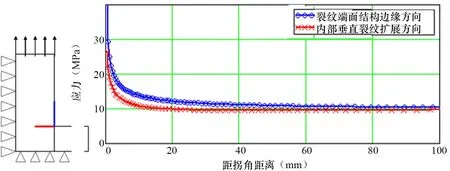
图2 二维直角结构不同分析方向的应力分布比较

3 三维拐角应力分布比较

典型三维结构是实际应用中普遍关注的问题。通过对6种典型三维结构(见表2)拐角处的应力分布进行比较，研究不同工况不同结构下各向的应力分布，为工程应用提供参考。

3.1 结构模型与参数

采用ANSYS-Multiphysics进行结构静力分析。各构件通用尺寸如表3所示，结构特性参数如表4所示，其中应力和弯矩的施加是参考了一般海况而进行的定性分析，分析目标为拐角处沿X方向的应力分布，其应力分析线如图3所示。

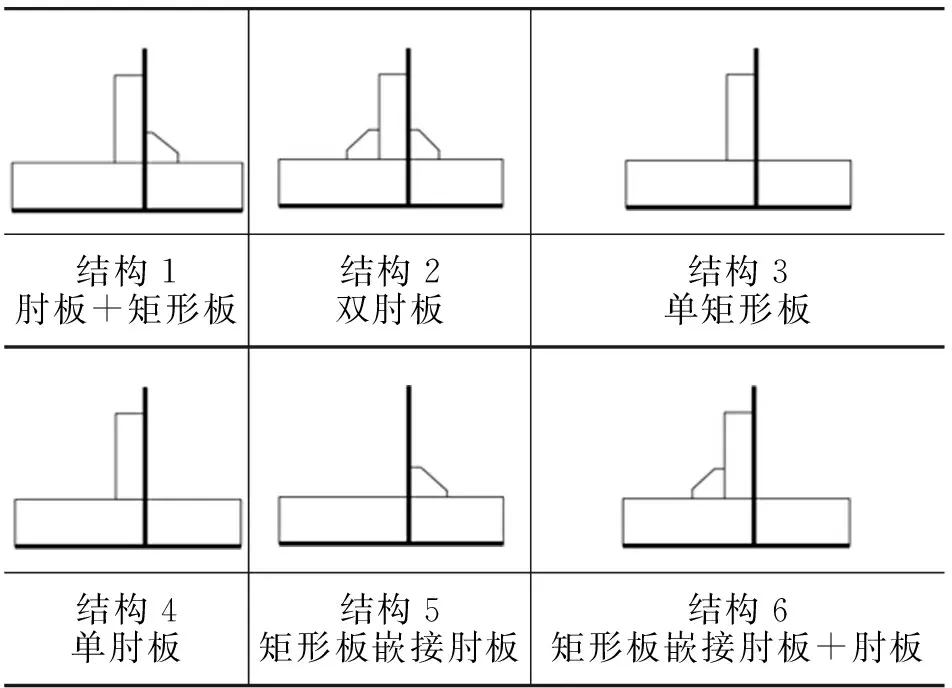
表2 典型三维结构拐角处应力分布比较

表3 各典型三维结构的尺寸参数

表4 结构分析特性参数

图3 典型三维结构与应力分析线

3.2 网格尺寸与划分

有限元分析中，网格的疏密性直接影响了数值模拟结果的准确性。为减小计算量，对于应力变化梯度较小部位，采用粗网格划分(2T，T为板厚)，对于应力变化梯度较大的结构拐角区域，采用细网格划分(T/60)。考虑到所求目标是拐角节点各方向的应力场，为了得到可观的应力分布，局部单元细化时并未采用EREFINE命令，而是基于LESIZE定义RATIO=0.01进行局部网格细化，网格总数为36 561(结构1)，由图4可知足够达到计算精度，合理可行。选取单元类型时，整体结构采用不考虑剪切形变的平面弹性壳单元SHELL63。而在建立刚性面时，对于主动点形心处应设置结构质量单元MASS21。

图4 典型三维结构局部网格细化示意图

3.3 边界条件与加载

针对3种工况(端面均布拉伸、施加弯矩及共同作用)，定义边界条件(C为刚性约束)，如表5所示。

表5 结构边界条件

外载荷施加采用定性分析，对于拉伸工况，基于SFL命令在端面线上施加应力，而载荷定义为单位面积上施加的力，所以端面各节点的均布应力为名义应力(100 MPa)与板厚(0.012 m)之积。对于弯曲情况，通过纵向构件端面建立刚性约束并施加弯矩，过程如下：

(1) 基于式(1)及式(2)求解两端面形心位置(±1 320, 53.33, 3.84)，并对形心定义质量单元(MASS21)，同时施加约束和弯矩载荷。

(2) 利用NSEL命令，选择纵向角钢两端面的全部节点，并使用CERIG命令以两端面形心为基点，与各端面所有节点形成刚性约束，建立刚性面。

(3) 利用F命令在两端面形心节点施加绕Z轴的弯矩载荷，使其达到中拱状态。由于研究的是拐角处应力分布奇异性对应力集中的影响，而在施加弯矩时，中拱状态相对于中垂状态更易使结构拐角处萌生裂纹，所以研究此种工况。

对于拉伸及弯矩载荷共同作用的工况，在弯矩载荷加载命令的基础上，通过拉伸载荷加载方式在结构纵向两端面线上施加载荷。各种工况下的边界条件及加载情况如图5所示。

图5 结构1在不同工况下的边界条件

3.4 结果运行与提取

通过/SOLU可完成结构模型分析，图6显示了拉伸、弯曲及它们共同作用下的位移云图及初始结构边缘情况，其满足了预计的结构变形需求。

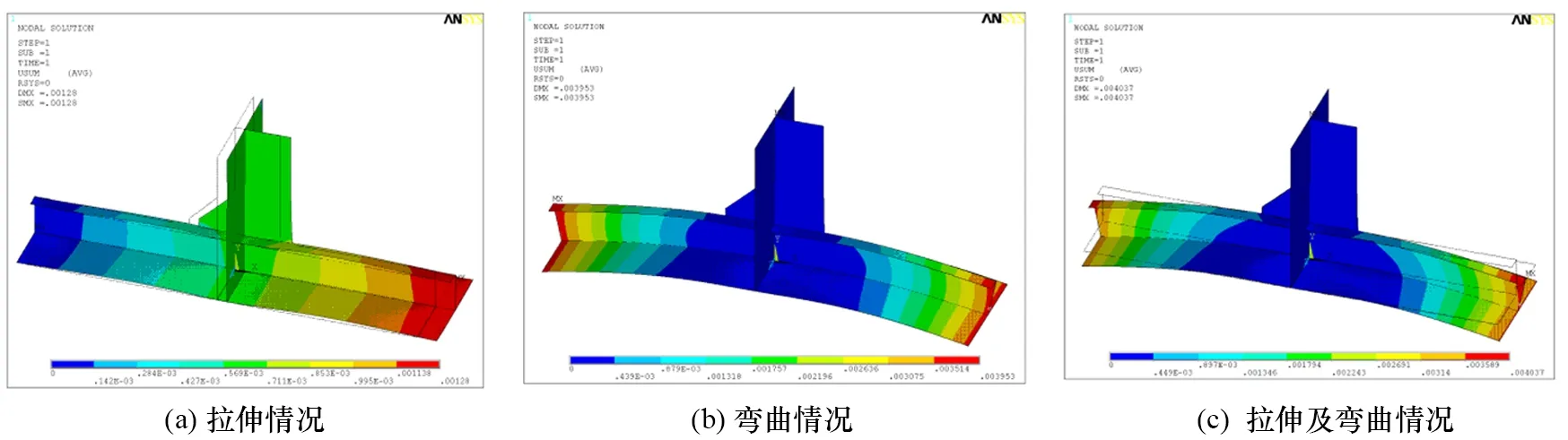
图6 结构1在不同工况下的的位移云图

分析结束后，需提取研究的拐角处各向应力分布值，这里以拐角处垂向应力分析线(Y轴)沿X方向的应力分布为例，主要命令流如表6所示。

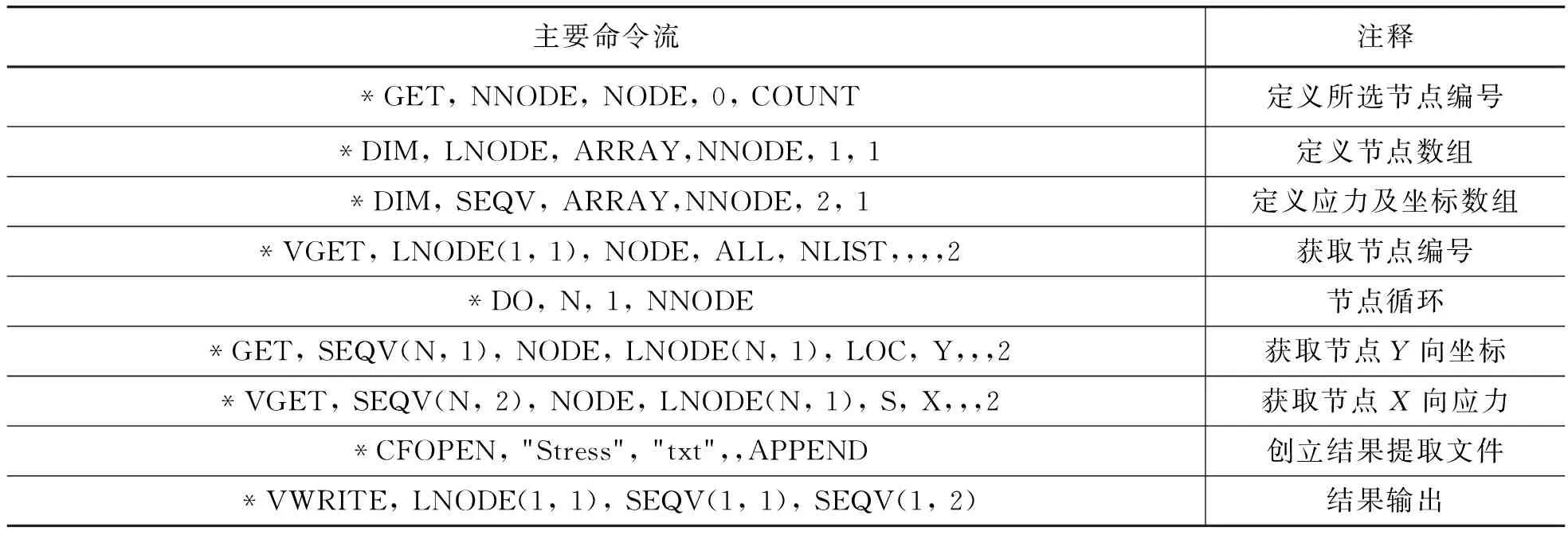
表6 垂向各节点沿X方向的应力结果提取主要命令流

4 工况分析

4.1 拉伸载荷工况

由于结构在纯拉伸的情况下，激励拐角节点萌生裂纹的主要因素是沿拉伸方向的应力，因此分析得到图7所示X方向的应力云图。可知舱壁板受载情况微弱，分析中可忽略，同时可见结构3和结构4的纵向构件的应力分布明显高于其它几种结构形式，强度最弱，在考虑整体结构强度时需谨慎采用。

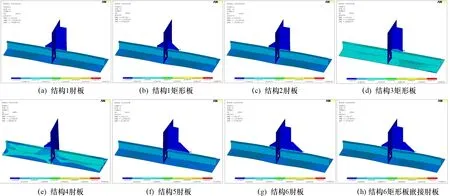
图7 拉伸载荷作用下拐角区域纵向的应力分布

图8比较了各向应力分布，可见分布大小情况分为三种趋势：

(1) 结构6中2种拐角的相对应力分布值最大；

(2) 结构1、结构2、结构5中4种拐角的相对应力分布值居中；

(3) 结构3及结构4拐角的相对应力分布值最小。

若以奇异强度理论薄板直角结构的奇异强度式as=min(H/2,L/25)进行说明，分析时应将各结构中的肘板等效成矩形板，近似估算了as(见表7)，发现L值大小决定了as，且as估算值满足三种大小趋势，即as越大，相对应力分布值越大。此外，由图1可知二维结构肘板处的应力分布相对于矩形板稍小，图8中同样可见三维结构(结构3及结构4)的应力分布也满足二维结构的趋势。

图8 拉伸载荷作用下拐角区域的应力分布比较

表7 不同结构拐角的奇异强度as近似估算 单位：mm

由于应力分布奇异性的存在破坏了X方向外载荷的平衡条件，从而引起了应力松弛现象。为保证结构应力平衡，即在应力分布平衡点以前奇异性区域面积需等于应力分布平衡点以后的松弛区域面积，如图9所示。应力分布奇异性的强弱，则决定了应力分布平衡点的位置和松弛区域应力分布曲线的斜率，即奇异程度越显著应力分布平衡点取值越小，松弛区域应力分布曲线的斜率增大表现越早，如图8(a)、 (b)、(c)所示。

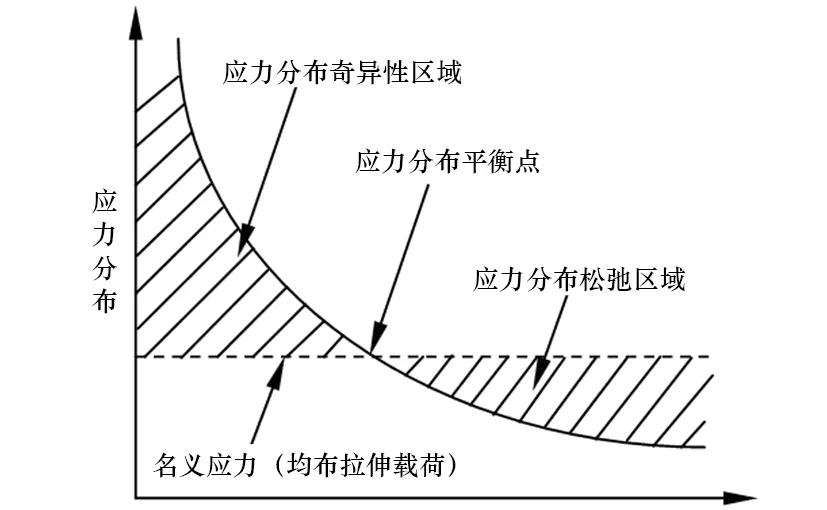
图9 外载荷平衡条件

图8(d)以结构1为例，显示了同一结构肘板和矩形板拐角处不同方向的应力分布，可见拐角处垂向和横向的应力分布差异微弱，仅在趋近拐角区域垂向应力分布值稍大。因此基于奇异强度理论分析典型三维结构时，对于仅受纵向拉压载荷的局部构件可适当简化面板，并通过增加腹板的厚度来保证结构强度，最终利用二维结构的奇异强度进行分析。

党的十八大报告指出，发展中国特色社会主义是一项长期的艰巨的历史任务，要毫不动摇坚持、与时俱进发展中国特色社会主义，不断丰富中国特色社会主义的实践特色、理论特色、民族特色和时代特色。中国共产党坚持并积极践行马克思主义群众史观就是不断丰富和发展中国特色社会主义实践特色和理论特色的重要表现。研究我们党群众史观生成的逻辑起点、不同历史时期和阶段的具体差异性表现等问题，对于贯彻落实党的十八大报告中关于开展群众路线教育实践活动、做好新形势下群众工作的精神，正确处理党群关系，巩固党的执政地位，维护社会政治稳定，构建社会主义和谐社会，进而实现中华民族伟大复兴的“中国梦”，都具有极其重要的启示意义。

分析拐角处的应力集中时，基于ANSYS的分析结果，图7已经给出了数值模拟下各结构拐角节点的应力SMX(/Pa)，但数值结果取决于网格细化程度，因此得到的拐角节点应力不可取。这里基于文献[7]中的线性插值法分析，由于插值法通常采用结构边缘沿载荷方向(纵向)的应力值，图8(d)也显示了纵向应力分布较大，以此求解拐角节点应力的准确性更高。进而，选择处于拐角一定距离的节点应力外插分析，并计算得到拐角处的热点应力σh及应力集中系数(SCF)，由表8可知计算结果满足上述应力分布大小趋势。

4.2 弯矩载荷工况

针对弯矩载荷作用下的中拱情况，研究激励结构拐角处裂纹萌生的纵向应力分布，可知抵抗弯矩载荷的主要结构是纵向角钢，同时在不同位置设立肘板或矩形板对加强结构有一定的作用，值得注意结构3和4中嵌接舱壁板的加强构件最少，导致了纵向角钢承载较大应力。因此，在波浪垂向交变载荷的作用下，合理的搭配纵向构件与加强构件对缓解拐角裂纹萌生有一定意义。

对弯矩载荷作用下结构拐角处的应力分布进行比较分析，由图10(a)、(b)、(c)可知拐角处不同方向的应力分布大小趋势，满足拉伸载荷作用下基于奇异强度理论的讨论，即舱壁板加强构件L尺寸与结构拐角处应力分布成正比关系。此外远离拐角节点区域的应力分布趋势如下：

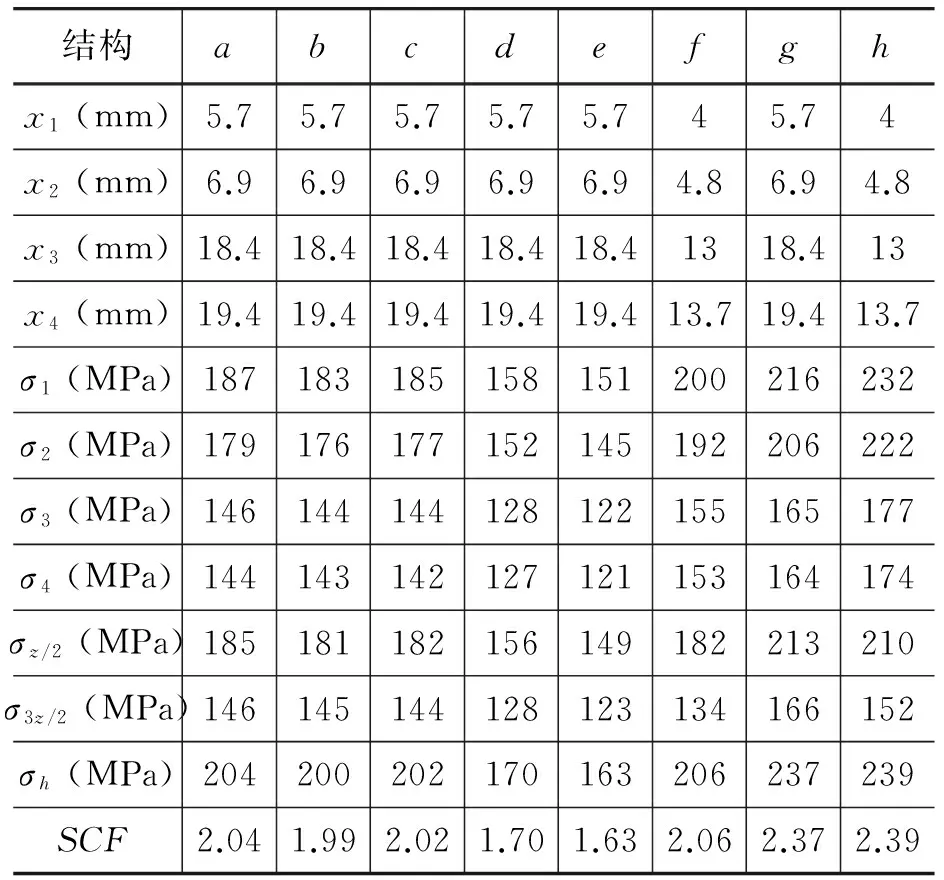
表8 拉伸载荷作用下拐角处的热点应力及SCF

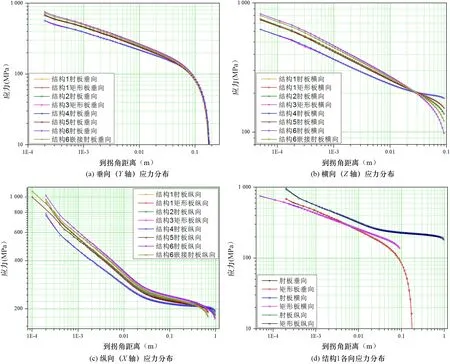
图10 弯矩载荷作用下拐角区域的应力分布比较

(1) 由于中拱时远离拐角处存在受压现象，因此垂向应力末端曲线急剧衰减；

(2) 由于应力平衡，不同结构的应力松弛程度需通过横向应力末端曲线体现；

(3) 由于纵向端面施加刚性约束，导致纵向应力曲线末端保持一定衰减程度。

通过图10(d)可知，基于结构1应力比较，纵向应力仍明显大于其它方向的应力，满足规范外插法中分析方向的要求，并计算了不同结构拐角节点处的热点应力，如表9所示。

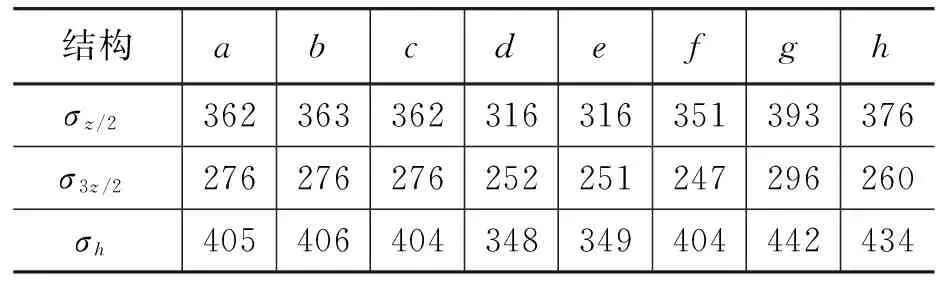
表9 弯矩载荷作用下拐角处的热点应力 单位：MPa

4.3 拉伸及弯矩载荷工况

在拉伸和弯矩载荷共同作用时，应力分布比较结果与弯矩载荷的作用结果相似，不再阐述。此外，拐角处的热点应力结果如表10所示，结果满足上述结论。

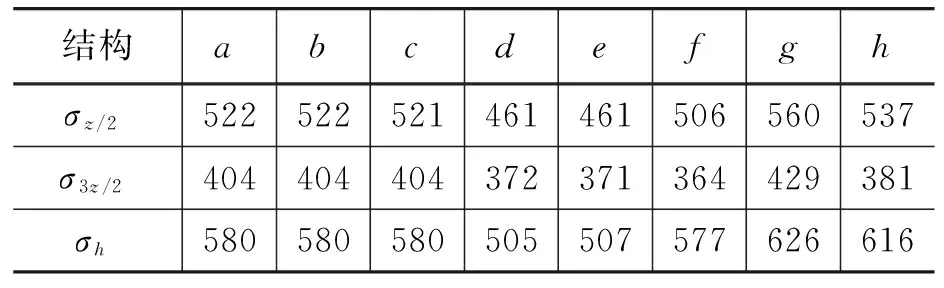
表10 拉伸及弯矩载荷共同作用下拐角处的热点应力 单位：MPa

进而考虑将拉伸载荷和弯矩载荷叠加分析，并与拉伸及弯矩载荷共同作用下的计算结果进行比较，如图11(a)、(b)、(c)所示。可见各向的应力分布吻合度较高，叠加结果略大于计算结果，且在趋近于拐角区域的误差一般小于6%，如图11(d)所示。因此，在实际分析中对于结构承受复杂载荷作用的情况，可以分解加载方式、边界条件，通过单独计算再叠加并减小约6%的误差得到近似准确值。同时基于叠加原理也可相互印证结果的准确程度。

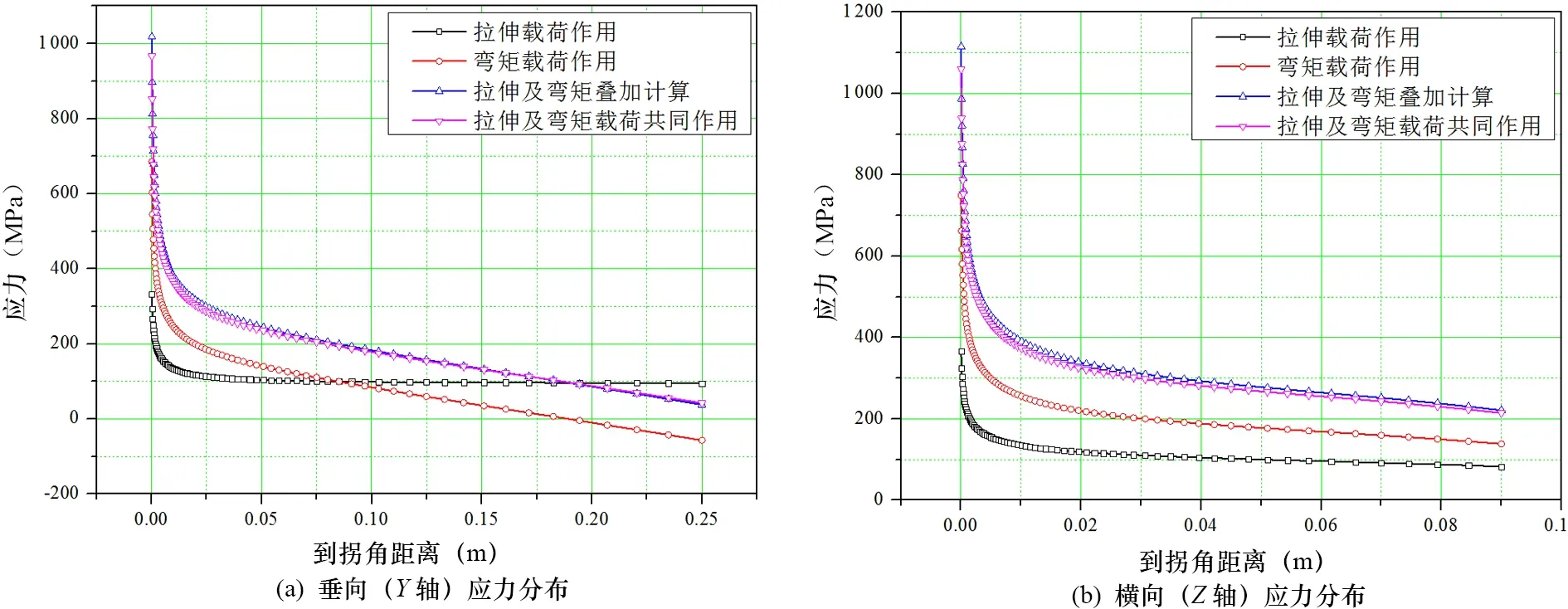
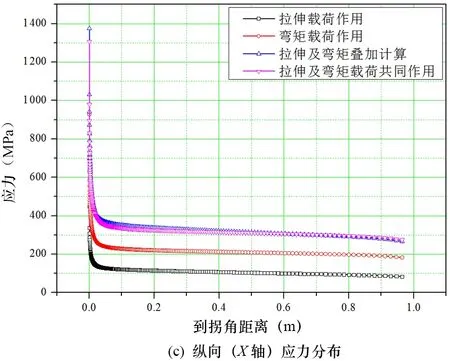
图11 结构1肘板拐角处的应力分布叠加分析

5 结论

本文基于奇异强度理论分析了二维结构拐角处的应力分布，通过研究4种结构及不同方向上的应力分布并基于奇异强度比较分析，得到二维135°拐角结构为缓解应力奇异性的最佳方案。进而针对6种典型三维结构的8处拐角，分别研究了在拉伸载荷工况、弯矩载荷工况及共同加载工况下的各向应力分布，得到各种结构适用的最佳方案。

(1) 考虑结构整体强度(抵抗纵向载荷、保证垂向支撑，缓解应力集中)时，结构1(肘板+矩形板)方案最佳；

(2) 考虑结构纵向强度，缓解应力集中而垂向无严重受载时，结构2(双肘板)方案最佳；

(3) 考虑明显缓解拐角节点处的应力集中，垂向不需要加强，纵向需要加强时，结构3(单矩形板)方案最佳；

(4) 考虑明显缓解拐角节点处的应力集中，纵向和垂向均不需要加强时，结构4(单肘板)方案最佳；

(5) 考虑结构纵向一侧强度，垂向需加强，缓解应力集中时，结构5(矩形板嵌接肘板)方案最佳；

(6) 考虑结构整体强度(抵抗纵向载荷、保证垂向支撑)，并适当缓解应力集中时，结构6(肘板+矩形板嵌接肘板)方案最佳。

其中，结构1(舱壁板两侧分别嵌接肘板和矩形板)为实际应用的最佳方案，也是基于奇异强度理论简化纵向角钢的面板，并得到各结构尺寸与奇异强度as关系的展望性研究对象。

[1] 高嵩, 徐丽, 王大政等. 基于奇异强度理论的疲劳特性评估方法[J]. 中国舰船研究, 2014, 9(5): 60-68,76.

[2] Williams M L. Stress singularities resulting from various boundary conditions in angular plates in extension[J]. Journal of Applied Mechanics, 1952, 19: 526-528.

[3] Gross R, Mendelson A. Plane elastostatic analysis of V-notched plates[J]. Fracture Mechanics, 1972, 8(3): 267-276.

[4] Lazzarin P, Tovo R. Notch stress intensity factor approach to the stress analysis of welds[J]. Fatigue and Fracture of Engineering Materials and Structures, 1998, 21(9): 1089-1103.

[5] 徐丽, 高嵩, Nigel Barltrop. 存在奇异点的结构疲劳评估简单方法[J]. 船舶工程, 2013, 35(6): 9-14.

[6] 高嵩, 徐丽, 王大政等. 基于奇异强度理论135°薄板拐角的应力评估方法研究[J]. 武汉理工大学学报, 2013, 35(12): 72-79.

[7] 中国船级社. 船体结构疲劳强度指南[S]. 北京: 人民交通出版社, 2007.

Comparative Research on Stress Distribution of Corner in Typical Hull Structure

GAO Song1, JI Yong-bo1, XU Li2, WANG Da-zheng2

(1.China Waterborne Transport Research Institute, Beijing 100088, China; 2. School of Naval Architecture and Ocean Engineering at Weihai, Weihai Shandong 264209, China)

To ensure the structural strength of the hull for the safe navigation, choosing a reasonable strengthening structure is essential. In this respect, taking the singular strength theory and numerical simulation with ANSYS to analyze the stress distribution and singularity of four kinds of typical two-dimensional structures on the corner. And then for six kinds of typical three-dimensional structure of marine, comparing the stress distribution in different directions at the corner of the structure under the conditions of tensile load, moment load and interaction respectively, also giving a better understanding of the finite element method. It is hoped that can be brought into real engineering.

Structural strength Stress distribution Singularity Finite element

高 嵩(1989-)，男，研究实习员。

U661

A