管道内壁粗糙度对沿程阻力影响的FLUENT数值模拟分析
2015-05-08姚雪蕾袁成清付宜风白秀琴
姚雪蕾,袁成清,付宜风,白秀琴
(武汉理工大学a.能源与动力工程学院可靠性工程研究所;b.船舶动力工程技术交通行业重点实验室,武汉 430063)
管道内壁粗糙度对沿程阻力影响的FLUENT数值模拟分析
姚雪蕾,袁成清,付宜风,白秀琴
(武汉理工大学a.能源与动力工程学院可靠性工程研究所;b.船舶动力工程技术交通行业重点实验室,武汉 430063)
针对在海底管道的设计阶段准确获取沿程阻力的问题,采用FLUENT软件运用数值模拟的方法,分析粘性流体在管道中的摩阻损失与管道内壁粗糙度的关系,将计算结果与理论结果进行对比。结果显示,除流态从水力光滑区到混合摩擦区间有一个过渡阶段存在误差外,其余都吻合良好,证实输油管道的内壁粗糙度只在混合摩擦区对摩阻有较大影响,改善管壁面粗糙度可以减小阻力。若流态处于水力光滑区到混合摩擦区之间,计算摩阻系数仅靠经验公式是不合适的,应考虑采用数值模拟计算的方法。
输油管道;粗糙度;沿程阻力;FLUENT;数值模拟
随着计算流体动力学的发展,利用FLUENT分析粘性流体在管道中的阻力特性已经得到了很多实用性的成果,如针对粗糙的管壁[1-4]或者是产生局部阻力损失的典型阀件(突扩管、三通管、弯管等)[5-6],通过数值模拟的方法可以模拟出常规实验无法得到的不同流场的各种信息。然而,目前工程上在管道的设计阶段,沿程阻力的确定一般只采用经验公式数学计算的方法,故考虑运用数值模拟的方法对其准确性进行验证,为管道设计中沿程阻力的获取提供依据。
1 沿程阻力与管道内壁粗糙度
管道的沿程阻力损失与管长、管流的速度分布,以及管壁的粗糙度等因素有关,通常用hf表示,按达西(Darcy-Weisbach)公式计算。
(1)
式中:L——管道长度;D——管道内径;v——流体流速;λ——摩阻系数。
相对当量粗糙度ε=2e/D。式中e为管壁的绝对当量粗糙度,是指管内壁凸起高度的统计平均值。研究表明,新的、清洁的管壁的绝对当量粗糙度仅取决于管材及制管方法,与管径无关;使用后的管路则随运行情况,如所输流体性质、腐蚀程度、运行年限、清管方法等不同而有显著变化[7]。
根据莫迪理论,一般可以把图分为5个区域:层流区、层流转变为紊流的过渡区、紊流水力光滑区、紊流混合摩擦区、紊流粗糙区[8-9]。在实际运行中,热原油管道上最常见的流态是水力光滑区,轻油管道也多在水力光滑区,输送低粘油品的较小直径管道可能进入混合摩擦区。所以本研究重点在紊流水力光滑区和混合摩擦区,摩阻系数λ与相对粗糙度ε的关系。
2 经验公式分析
从莫迪图可以定性看出,水力光滑区中相对粗糙度ε变化,摩阻系数λ不变;而混合摩擦区的摩阻系数λ会随相对粗糙度ε的减小而减少。然而,不能明确地观察出λ随ε定量变化的形态和趋势。因此,以工程上常应用的米勒公式(式2)和Colebrook-White公式(式3)为基础(见表1),以相对粗糙度ε为变量,雷诺数Re为参量进行数学计算,研究粗糙度对输油管道摩阻系数的影响,得出摩阻系数随相对粗糙度变化曲线[10]。
计算结果见图1。其中由于公式(2)为λ的隐函数,故利用埃特金法[11]进行迭代求得近似解。总体上可发现摩阻系数随相对粗糙度的减小而减小,与莫迪图结果一致。并且在相对粗糙度较大的区域,摩阻系数减小的更明显,而在相对粗糙度较小的区域,摩阻系数减小幅度较小,并趋于稳定。高雷诺数管内流体要在相对粗糙度较小下才处于水力光滑区,相比低雷诺数下的流态更容易处于水力光滑区,稳定区域更大。但水力光滑区的摩阻系数随雷诺数减小而增大。

表1 λ的经验公式
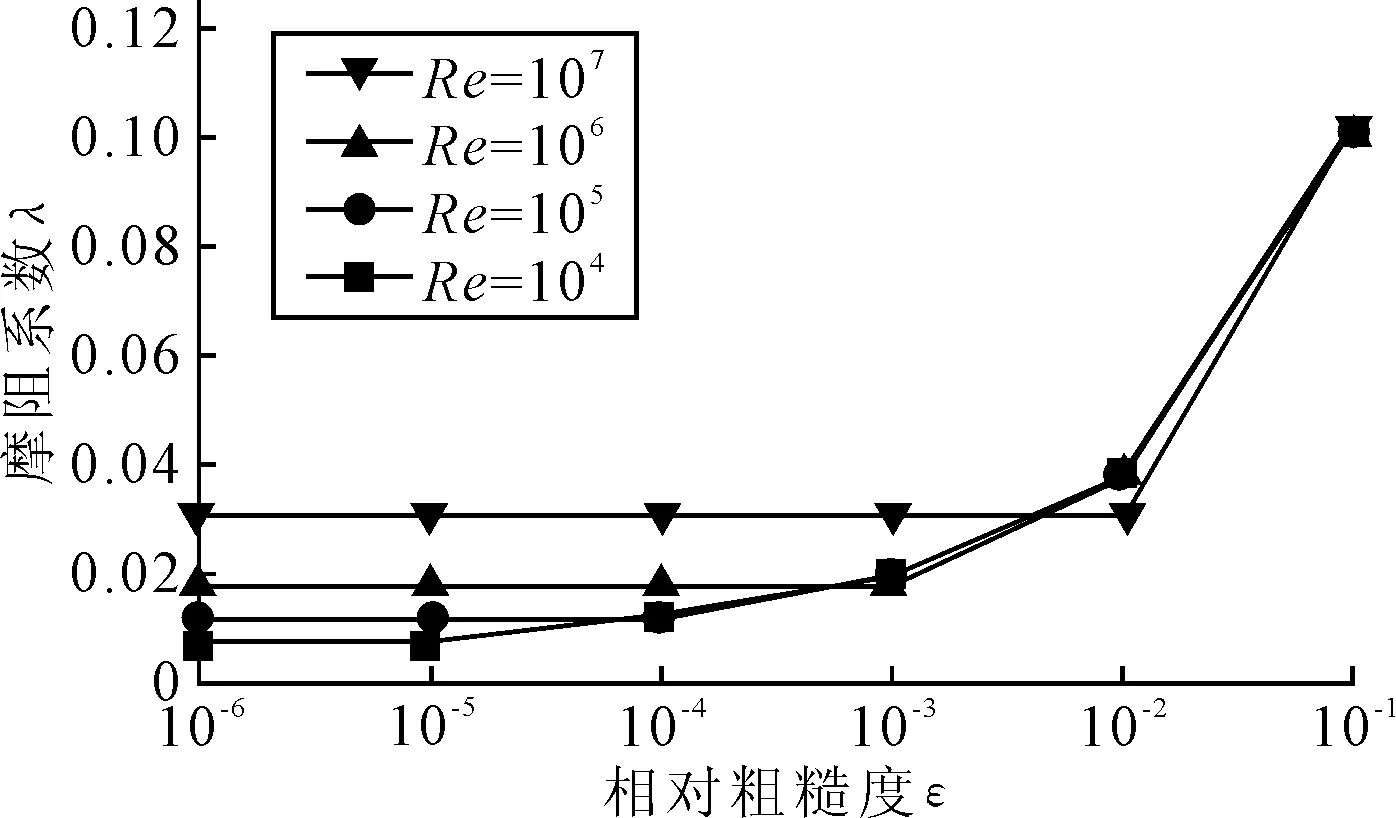
图1 摩阻系数随相对粗糙度变化
在上述计算过程中,判断流态为紊流水力光滑区还是混合摩擦区是以临界雷诺数Re1为标志分界线,其值由管道层流边界厚度与绝对当量粗糙度的比值推导而来。
(4)
对于某一直径的管子,其临界雷诺数的数值取决于管壁绝对当量粗糙度。故当管内油流的雷诺数接近临界值时,合理确定粗糙度数值,成为准确判别流态区和计算λ的关键因素。从另一方面来看,式(4)中Re1值是根据勃拉休斯(Blasius)公式等经验公式得来的,若采用不同的公式推导,将会得出不同的计算式。因此,根据临界值来划分流态区只是近似的,实际管道中流态从水力光滑区到混合摩擦区变化有一个过渡阶段,使用经验公式对过渡阶段的λ值计算不够准确,需查询莫迪图或进行试验来修正。
雷诺数为104~105情况下,分别查莫迪图[9]及用公式计算得到摩阻系数λ,绘制临近过渡阶段的摩阻系数随相对粗糙度变化曲线见图2。
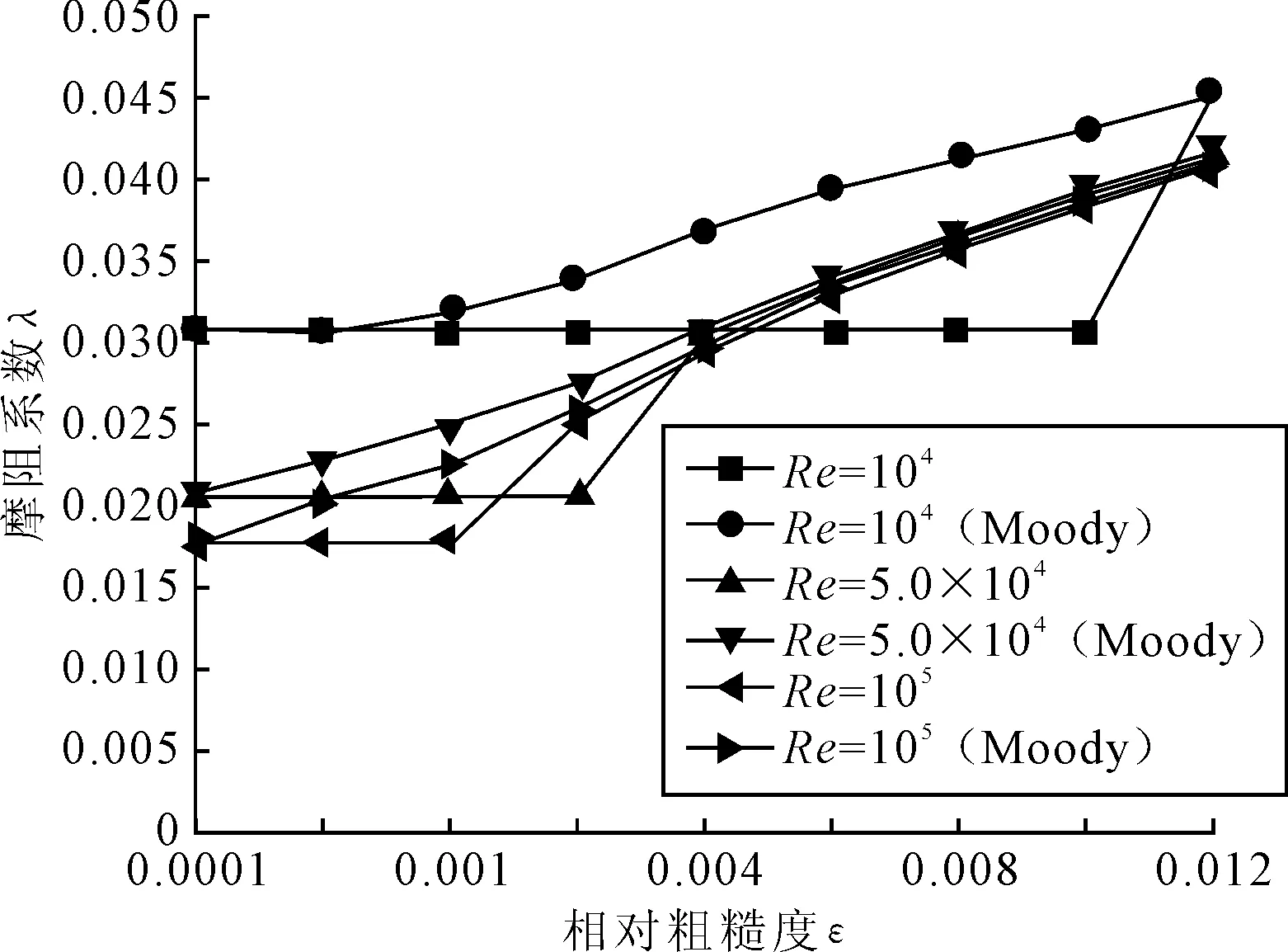
图2 过渡阶段摩阻系数随相对粗糙度变化
由图2可见,若根据理论公式计算,粗糙度较小时,流体处于在水力光滑区摩阻系数不随粗糙度变化而变化,曲线是一条直线;随着粗糙度增大,当进入混合摩擦区时,λ才开始随相对粗糙度增大而增大。而实际上摩阻系数λ并不是在临界雷诺数时突变,而是在Re接近Re1前就开始逐渐增大。同时还可以发现,在这一过渡阶段之外,公式计算得出的λ值与莫迪图查询的值都很相近,也证明了米勒公式和Colebrook-White公式在多数工业管道流体中是适用的。
3 基于Fluent的数值模拟
研究流体流动问题的完整体系由传统的理论分析方法、实验测得方法及CFD数值方法组成,各有优缺点,但又有很多联系,在实际工程中将三者进行有机的结合能得到更合理的结果。用经验公式对管道内流体进行摩阻计算实际上还不够完善,特别是对于黏性流体在管中的流动,某些情况下得到的λ值并不准确,还需要通过实验进行模拟和验证。但实验常受到诸多因素的限制,且经费投入较大,相形之下,CFD更有优势。分析流体流动的基本方程主要是质量守恒、动量守恒、能量守恒三种方程。如果流动涉及不同组分的混合或是相互作用,还要遵守组分守恒定律。在实际计算时,还要考虑不同的流态,对于湍流,目前工程中一般是对瞬态N-S方程做时间平均处理,同时补充反映湍流特性的其他方程,如湍动能方程和湍流耗散率方程等[12]。
本研究中基于FLUENT软件进行三维数值模拟。模拟对象为一段直管内油品的湍流流动。通过改变入口端流速v来控制雷诺数Re,并分别在不同管壁粗糙度下进行数值模拟,得出处于管中试验段某两端面的压力的差值,根据伯努利方程和达西公式联立计算即可得到沿程损失阻力系数λ,再将所得的值与莫迪图曲线或经验公式计算得出的数值对比,判断其是否正确。
3.1 物理模型
在GAMBIT中建立直径300 mm,长4 m的圆截面直管,其中前3 m是前置段,用来让湍流充分发展,后1 m为试验段。管内流体选取我国中原地区原油,基本参数:50 ℃密度846.6 kg/m3,运动粘度10.32 mm2/s。
3.2 划分网格
管内流体的阻力主要是流体与壁面间的作用产生的,在壁面附近会有较大的速度梯度。故在端面上创建边界层网格加密。具体设置为:first per centage(第一层边界层网格的高度关于宽度的百分比)为20,Growth factor取1.2,rows取5层。端面网格划分采用默认方式,单元格为四边形,网格个数count设为50。得到mesh faces为473,体网格mesh volumes为100 276。网格划分情况见图3,图中坐标X方向为流向,Y、Z方向为径向。
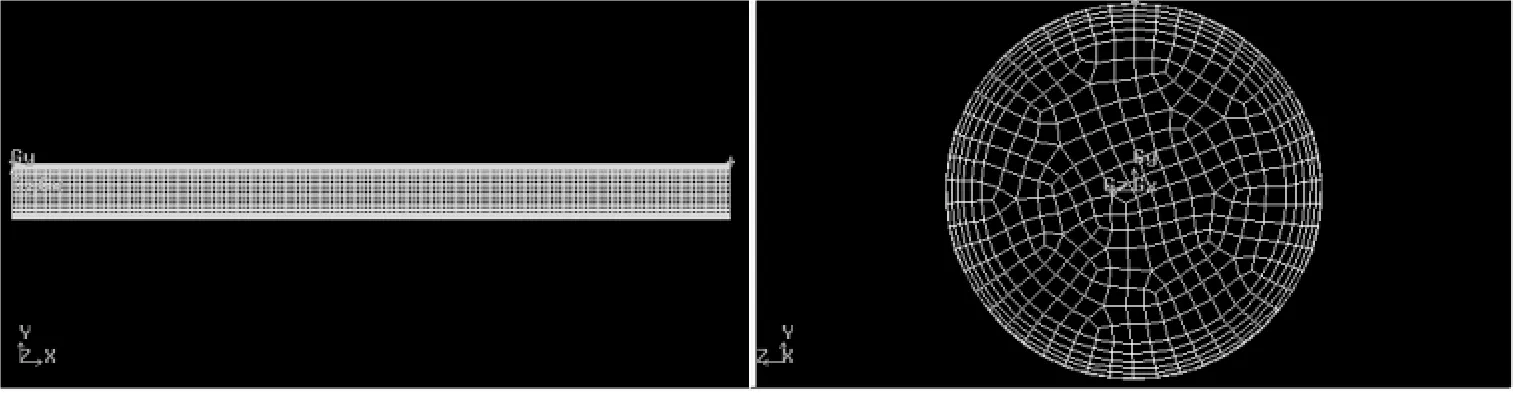
图3 模型网格划分
后续模拟计算中,经过测试,在此网格密度上即使再提高其密度,对计算的精确性也无法进一步明显的提高,而计算量反而大大增加。因此选用此密度进行网格划分可达到计算要求。
3.3 边界条件与初始化
将在GAMBIT中划分好的网格文件导入FLUENT中。采用标准的k-ε湍流模型与标准壁面函数法(Standard wall function),变化参数主要有两个:①入口速度及相关的湍流参数;②壁面粗糙度。具体设置如下。
1)模型求解器(Solver)选择压力基、显式、定常流。
2)粘性模型(viscous model)选择双方程模型(k-epsilon[2 eqn]Standard)。
3)流体材料设置为原油。
4)速度进口(velocity-inlet)边界条件设置为入口端速度,变化范围为2~6 m/s。湍流方法指定为湍流强度I与水力直径DH,充分发展的管流核心湍流强度I可按经验公式来估算。
(5)
式中:ReDH——以水力直径为特征长度求出,水力直径定义为流通面积与湿周比值的4倍。
5)出流(outflow)边界条件保持默认值。
6)固壁(wall)边界条件设置壁面粗糙度(wall roughness),在此默认粗糙度厚度值KS(roughness height)等同于绝对当量粗糙度e。变化范围为0.05~0.30 mm;粗糙度常数CS(roughness constant)保持默认值0.5,认为管壁粗糙度均匀分布。
7)其他条件如求解方法(Solutions)等默认FLUENT的初始设定,使用进口的量对全场完成初始化。
3.4 迭代计算
计算何时收敛对结果的准确性有重要影响,本研究中,模型的收敛采用两个判断标准,一是监视每个守恒值的残差,X、Y及Z方向速度的残差分别要求低于1×10-7,连续性的残差低于1×10-2,湍动能k和耗散率ε的残差低于1×10-6。另一个是出口流量值,只有当出口流量值稳定,且入口流量与出口流量近似相等时,才可以判定为收敛。完成以上所有设定后,开始迭代计算。
4 FLUENT计算结果
4.1 试算情况
以入口速度设置为2 m/s,粗糙度为0.05 mm的边界条件为例,使用标准的k-ε湍流模式对该模型进行试算。迭代停止后各方向速度及连续性残差监测见图4。
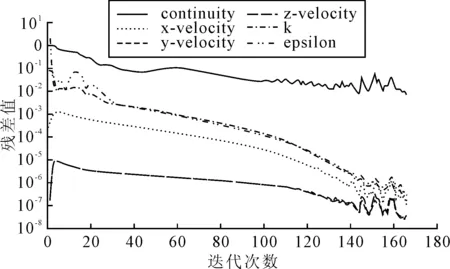
图4 残差监控
由图4可见,其收敛条件已经符合上述要求。另外,质量流量通量报告表明,出口与入口的质量流量误差为4.577 636 7×10-5,也表明计算收敛,应用FLUENT软件对本例的计算是可行的。
管道出口速度在径向上的变化见图5,轴线压降见图6。
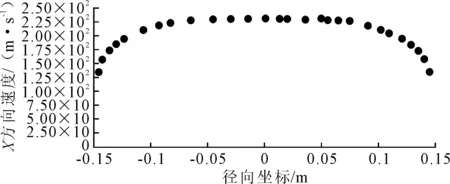
图5 出口速度径向分布

图6 轴线压降
由图5、6可见,管道后端速度呈充分发展状态,压降呈线性。可知此模型计算域选取足够长,可应用FLUENT进行模拟计算。
4.2 计算结果分析
通过FLUENT的Report菜单中的surface Integrals命令可以获得圆管任一端面的面积加权平均压强值。模拟选择x=3.4 m和x=3.9 m两端面的计算值,分别记为pa1和pa2,通过其压强差得到沿程阻力损失进而算得摩阻系数λ。
(6)
式中:D——管径0.3 m;L——距离0.5 m;ρ——密度,846.6 kg/m3;v——流速,m/s。
为了验证FLUENT仿真的准确度,将模拟计算值λ1与通过按表1中经验公式计算得出的数值λ2进行对比。结果对比见到表2。
由表2可见,若流态为水力光滑区,基于FLUENT仿真的模拟计算结果与经验公式计算值基本接近,最大误差为2.33%。在此状态下对三维管道的数值模拟取得了合理的结果,并具有较高的计算精度。而流态为混合摩擦区时,基于FLUENT的模拟计算结果与经验公式计算值误差较大,最大误差绝对值达15.65%,数值模拟没有达到较好的效果,需要分析误差原因。
1)流态为水力光滑区时,相对粗糙度ε变化,摩阻系数λ几乎不变。模拟计算结果符合理论,证明了摩阻系数λ只和雷诺数有关,与相对粗糙度ε无关。
2)当雷诺数Re很接近临近雷诺数Re1的值时,模拟计算的摩阻系数λ开始逐渐增大,但不显著。例如流速为3 m/s,粗糙度为0.25 mm时λ值较之前不随粗糙度变化的λ的值增大率为1.8%,与公式计算值的误差为2.23%,此时Re比Re1只近似小于1 800。分析认为FLUENT的数值模拟结果可以证明,出现此变化的原因应该是管道中的流态变化有一个过渡阶段,实际上摩阻系数λ并不是在临界雷诺数时突变,而是在Re接近Re1前的过渡阶段就开始逐渐增大。
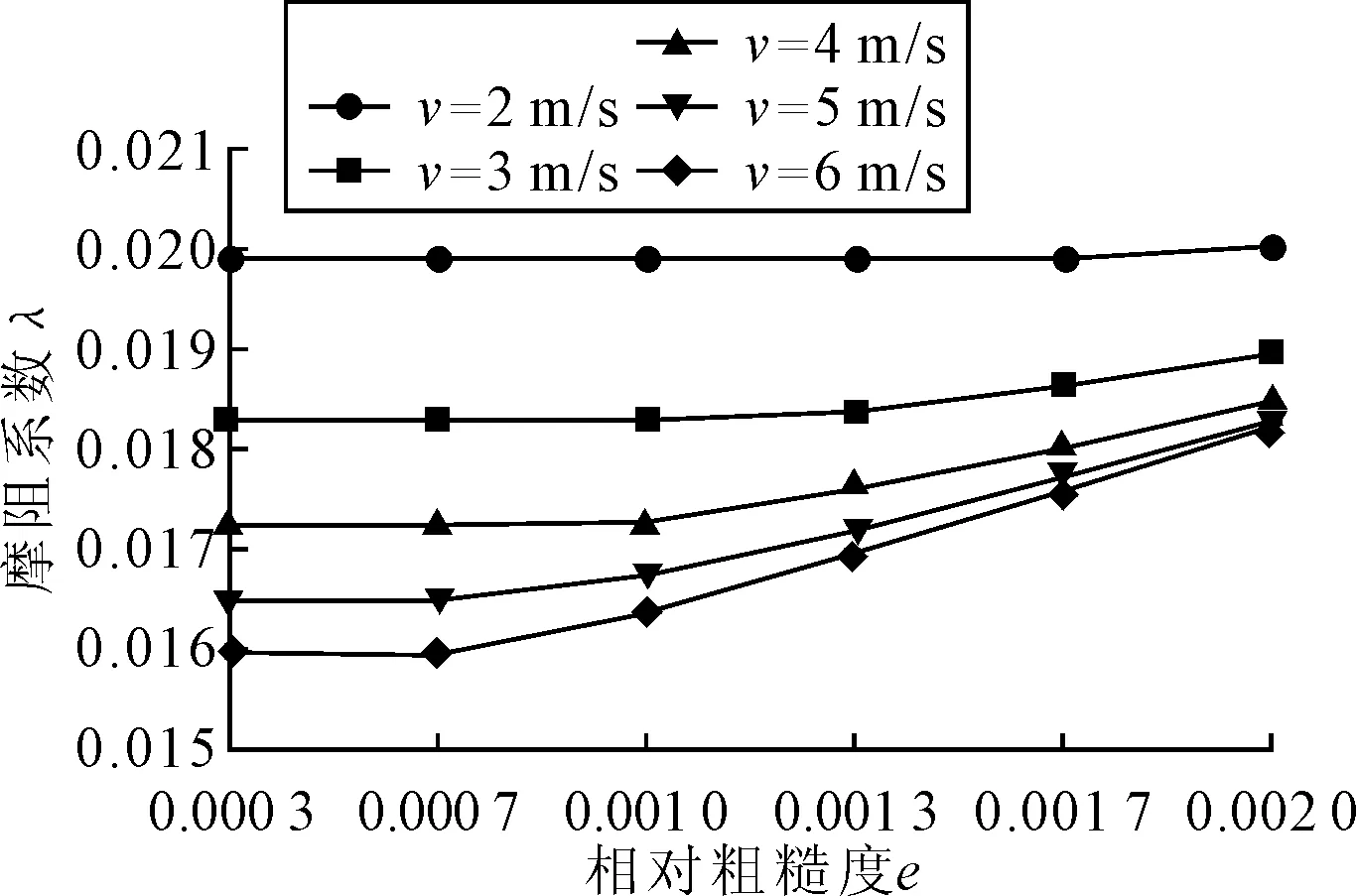
图7 数值模拟计算的λ随ε变化
3)流态为混合摩擦区时,数值模拟的值与公式计算值有较大的误差,使用标准k-ε湍流模型进行数值模拟的值小于经验公式计算值。但变化趋势相同,如图7,和前面的分析一致,符合莫迪图。证明λ与Re和ε均有关,在雷诺数相同时,λ随ε增大而增大。
4.3 误差原因
1)经验公式使用的是科尔布鲁克-怀特(Colebrook-White)公式,通过试算迭代得到的近似解是不精确的。
2)由于湍流模式和数值计算中都有不可避免的误差,同时模拟的管道中流体可能处于水力光滑区至混合摩擦区间的过渡阶段,不完全适用于科尔布鲁克-怀特公式或数值模拟。从数据上来看,随着雷诺数增大,λ误差整体上从15%下降为14%。由此可以推测,流体雷诺数比临界雷诺数Re1大得越多,较完全地处于混合摩擦区时,模拟的计算值越有符合经验公式值的趋势。

表2 模拟计算与公式计算结果对比
注:流态Ⅱ表示为水力光滑区,Ⅲ表示为混合摩擦区。
3)标准k-ε湍流模型在壁面区使用了不够精确的近壁函数的半经验公式,需要修正模型或精细网格。
为了验证猜想2),选取几组参数进行数值模拟,让Re值适中地处于Re1和Re2值之间。其中Re2为判断混合摩擦区和粗糙区的临界雷诺数,计算式见表1。数据处理同前。结果见表3。
结果表明,数值模拟得到的λ与经验公式值误差很小,符合猜想2)。通过FLUENT的数值模拟发现,水力光滑区至混合摩擦区间的过渡阶段(Re值接近于Re1的值)的流态,不完全适用于科尔布鲁克-怀特公式,或是使用标准k-ε湍流模型进行数值模拟。当流态较完全地处于混合摩擦区时的结果更吻合,能适用于工程。
为了验证猜想3),对模型划分了更精细的网格。具体设置为:first percentage取18,Growth factor取1.1,rows取6层。端面网格划分采用默认方式,单元格为四边形,网格个数count设为5。得到mesh faces为616,体网格mesh volumes为146 608。使用标准k-ε湍流模式中非平衡壁面函数法(Non-Equilibrium Wall Function)。以流速为6 m/s,粗糙度为0.3 mm为例,结果见表4。

表3 计算结果

表4 计算结果比较
结果表明,计算精确性没有明显提高,而计算量却大大增加。由此判断猜想3)不是产生误差的最主要原因。使用更精细的模型要付出更大的模拟计算量和时间,不适用于工程实际应用。
5 结论
1)数值模拟证实了输油管道的内壁粗糙度只在流态为混合摩擦区对摩阻有较大影响,即摩阻系数λ随相对粗糙度ε的增大而增大。且摩阻系数的变化幅度与粗糙度成正比,在相对粗糙度较大的区域,摩阻系数增大的更明显,在相对粗糙度较小的区域,摩阻系数增大的幅度较小;
2)经验公式推知流态区的划分只是近似的,当流态处于变化临界时摩阻系数用经验公式计算的准确性有待验证。仿真分析表明,管道中的流态从水力光滑区到混合摩擦区间有一个过渡阶段,在这一阶段摩阻系数λ随与相对粗糙度ε增大而小幅度增大。因此,若想获取准确的沿程阻力,在此阶段计算摩阻系数仅靠经验公式是不合适的,数值模拟计算是应考虑的方法;
3)在过渡阶段之外,流态可以认为是完全处于水力光滑区或混合摩擦区。在此种情况下,经验公式计算、莫地图查询与数值模拟得出的λ值都很相近,证明了米勒公式和Colebrook-White公式在多数工业管道流体沿程阻力计算中具有一定的适用性和准确性。
[1] VIJIAPURAPU,S, JIE C. Numerical Simulation of Turbulent Flow in a Ribbed Pipe Using Large Eddy Simulation[J]. Numerical Heat Transfer, Part A: Application(ISSN:1040-7782), 2007,51(12):1137-1165.
[2] VIJIAPURAPU,S,.& JIE C. Performance of turbulence models for flows through rough pipes[J], Applied Mathematical Modelling(ISSN: 0307-904X), 2010,34(6):1458-1466.
[3] ZHANG,Y B & Che,D F. Numerical simulation of turbulent flow and wall mass transfer in a rectangular channel roughened by v-shaped grooves[J],Numerical Heat Transfer,Part A:Application(ISSN:1040-7782),2014,66(5):551-581.
[4] 张建卓, 李康康, 高 猛,等. 粗糙度对流体泄漏和摩擦阻力的仿真研究[J].微计算机信息,2011,27(6):238-240.
[5] 孙 琳.圆管突扩(缩)局部阻力试验及流场数值模拟[D].哈尔滨:东北农业大学,2010.
[6] 赵 月.基于CFD的管道局部阻力的数值模拟[D].大庆:东北石油大学,2011.
[7] 杨筱蘅.输油管道设计与管理[M].北京:中国石油大学出版社,2001.
[8] 杨树人,汪志明,何光渝,等.工程流体力学[M].北京:石油工业出版,2006.
[9] 詹德新,王家楣.工程流体力学[M].武汉:湖北科学技术出版社,2001.
[10] 杨晓鸿,朱薇玲.粗糙度对输气管道摩阻系数的影响[J].石油化工设备,2005,34(1):25-28.
[11] 罗祖帖,Excel在管路阻力计算中的应用[J].化肥设计,2004,42(2):15-17.
[12] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004.
Numerical Simulation of Effect of Wall Roughness on the On-way Resistance Based on FLUENT
YAO Xue-lei, YUAN Cheng-qing, FU Yi-feng, BAI Xiu-qin
(a. Reliability Engineering Institute, School of Energy and Power Engineering; b. Key Laboratory of Marine Power Engineering and Technology (Ministry of Transport), Wuhan University of Technology, Wuhan 430063, China)
Aiming at the problem of obtaining accurately the on-way resistance of submarine pipeline at the design stage, numerical simulation method is adopted to analyze the relationship between loss of viscous fluid friction and wall roughness of the pipeline based on FLUENT. Comparing the calculated results with theoretical results and the actual situations, the results show there is a good agreement, except for the flow pattern transiting from the hydraulic smooth region to the mixed friction region. It is confirmed that the friction coefficient is strongly influenced by pipeline wall roughness only in the turbulent mixing friction region. In this case, reducing the surface roughness of the wall can cut down the resistance. If the flow pattern transits from the hydraulic smooth region to the mixed friction region, it is inappropriate to calculate friction coefficient only by the empirical formulas, and numerical simulation is the method that should be considered.
oil pipeline; roughness; on-way resistance; FLUENT; numerical simulation
10.3963/j.issn.1671-7953.2015.06.024
2015-07-17
国家自然科学基金优秀青年基金项目 (51422507)
姚雪蕾(1992-),女,硕士生
TE832;P756.2
A
1671-7953(2015)06-0101-07
修回日期:2015-09-10
研究方向:摩擦学系统及表面工程
E-mail: yaoxuelei2013@outlook.com
