兆瓦级风力机塔架的有限元非线性屈曲分析

唐瑞宏， 汤赫男， 许增金， 王世杰

（1.沈阳工业大学 机械工程学院，沈阳 110870；2.沈阳鼓风机集团风电有限公司，沈阳 110869）

0 引言

我国风能资源丰富，近几年风电事业得到长足发展，但我国风力机设备制造，设备利用率和风力机基础设计等一系列技术问题还有待于进一步解决。其中，最亟待解决的是塔架损坏的问题，据不完全统计，在诸多风力机的损坏形式中，塔架的折断占到了18%，位居各项破坏形式之首，这说明目前塔架的设计还存在缺陷。塔架是风力机重要的承载部件，它除了支撑风力机的重量之外，还要承受风压力和风力机运行中的动载荷。塔架可以近似看成一种细长体薄壁结构，在轴向压力的作用下易发生屈曲失稳，设计时必须特别关注其稳定性。研究塔架稳定性问题，需要借助于有限元屈曲分析方法。屈曲分析是用于确定结构处于失稳临界状态时的屈曲载荷和屈曲模态的一种技术手段。ANSYS中提供了两种进行屈曲分析的方法：线性（特征值）屈曲分析和非线性屈曲分析。线性屈曲分析即传统的理想线弹性屈曲分析方法，然而非理想和非线性行为阻止了实际结构达到该理论极限载荷预计的阶段，故线性屈曲分析会产生非保守的结果。而非线性屈曲分析可以得到更精确的屈曲载荷，是打开大变形效应开关的一种静力分析，考虑结构的初始缺陷和材料非线性等特性。非线性屈曲分析提取线性屈曲分析结果作为非线性屈曲的几何缺陷，然后逐渐对结构加载，该过程一直进行到结构的极限载荷或最大载荷为止。研究塔架稳定性的目的在于确定塔架在轴向压力作用下的临界载荷及其相应的屈曲模态，以加强安全措施，提高结构的抗失稳能力［3］。本文借助于 ANSYS12.0有限元软件，对2MW78m风力机塔架进行非线性屈曲分析，分析塔架门对塔架稳定性的影响。

1 塔架有限元模型的建立与加载

1.1 单元类型的选择

SHELL93为8节点弹性壳单元，可以很好地模拟曲壳，该单元的每个节点有6个自由度，即沿节点坐标系x、y和z方向的平动位移和绕各轴的转动位移［1］，采用壳单元SHELL93模拟塔架结构，分为是否存在塔架门的两种类型，分别对塔架进行有限元屈曲分析计算。

1.2 塔架参数

塔架为圆筒形式，是目前风力机普遍采用的典型结构形式。该塔架的高度为78 m，最大壁厚为30 mm，最小壁厚为12 mm，塔底外径为2.15 m，塔顶外径为1.477 5 m。材料为Q345钢，屈服强度为345 MPa，泊松比为0.2，弹性模量为2.1×1011Pa，材料密度为7 850 kg/m3。

1.3 加载方案

有限元分析的关键问题在于将实际工程系统的物理模型转化为相应的数学模型。风力机塔架内部设有一些附属设备：如平台、爬梯、通风口等。有限元分析时，可以对塔架几何模型作适当简化，原则是在保证整体计算精度的前提下，简化一些与塔架稳定性分析无关或承载非关键的部位，以提高计算速度。

坐标原点在塔架底部中心处，Z轴正向为垂直底面向上。塔架底端全约束，顶端施加方向沿Z轴反方向的单位载荷，塔架整体受重力作用，重力加速度为-9.8 m/s2。其中有塔架门模型的单元数为4 572个，节点数为13 650个。有塔架门的壳单元塔架的有限元模型，如图1所示。

图1 有塔架门的壳单元塔架的有限元模型

2 有限元屈曲分析

2.1 经典ANSYS非线性屈曲分析过程

1）打开预应力开关选项，进行线性屈曲分析；

2）设置几何缺陷，逐渐对结构加载；

3）采用线性搜索方法，进行非线性屈曲分析；

4）结果后处理，建立载荷和位移关系曲线，确定结构的非线性临界载荷。

图2 无塔架门线性屈曲第一阶等效应力图

图3 有塔架门线性屈曲第一阶等效应力图

2.2 屈曲有限元结果分析及校核

2.2.1 线性屈曲结果分析

打开预应力开关选项，进行线性屈曲分析。由线性屈曲分析结论可知，无塔架门线性屈曲第一阶特征值是0.499 02×108，而有塔架门线性屈曲第一阶特征值是0.494 39×108。从计算结果中可以看出：无塔架门线性屈曲特征值大于有塔架门线性屈曲特征值，这说明无塔架门的塔架稳定性优于有塔架门的塔架，即塔架门的存在会降低塔架抵抗屈曲失稳的能力。无塔架门线性屈曲第一阶等效应力图，如图2所示。有塔架门线性屈曲第一阶等效应力图，如图3所示。

2.2.2 强度校核

通过ANSYS后处理功能，可直观形象地将塔架的强度分析结果表示出来，如图2、图3所示。

强度检验条件：σmax<［σ］，其中σmax为计算出的最大应力，［σ］为材料许用安全应力。塔架材料的屈服极限σs=345 MPa，则其许用应力为：［σ］=σs/n，n 为材料的安全系数。根据 GL规范，n=1.1，则［σ］=313.6 MPa。其中ANSYS计算出的无塔架门塔架的最大应力值小于许用应力，强度满足设计要求；有塔架门塔架的最大应力值大于许用应力，强度不满足设计要求，需考虑门框加强设计。

2.2.3 非线性屈曲结果分析

1）无塔架门塔架非线性屈曲结果分析。由线性屈曲分析结论可知，无塔架门线性屈曲的载荷因子达到0.499 02×108时发生屈曲，对于非线性屈曲，载荷因子达到0.48×108时发生屈曲，选取应力最大节点776号位移载荷图，如图4所示。非线性屈曲因子小于线性屈曲因子，非线性屈曲结果更为保守。

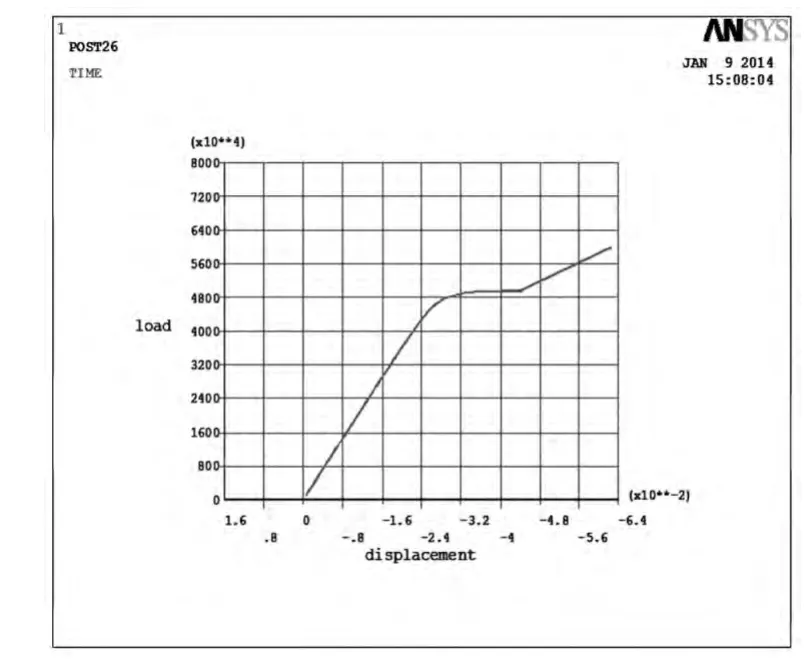
图4 节点776号位移载荷图

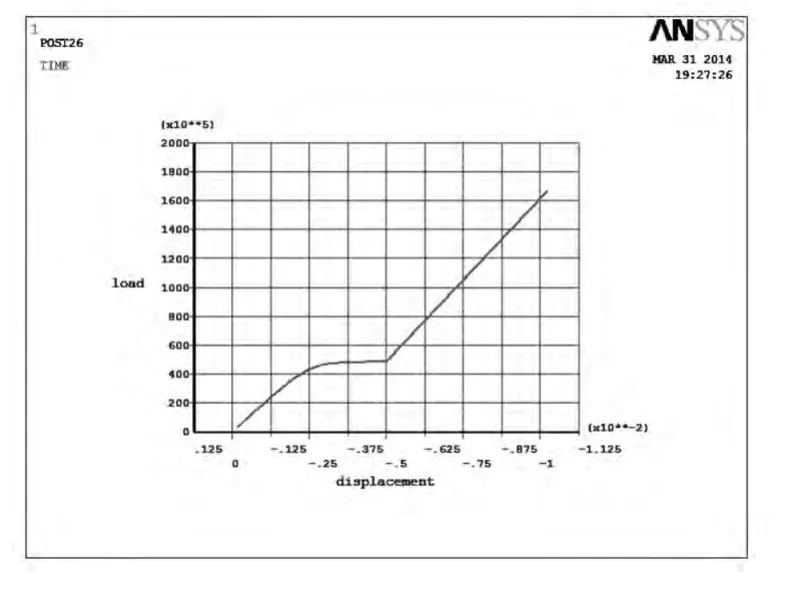
图5 节点32号位移载荷图

2）有塔架门塔架非线性屈曲结果分析。由非线性屈曲分析结论可知，有塔架门塔架线性屈曲的载荷因子达到0.494 39×108时发生屈曲，对于非线性屈曲，载荷因子达到0.46×108时发生屈曲，选取应力最大节点32号位移载荷图，由图5所示。非线性屈曲因子小于线性屈曲因子，同样产生保守结果。

2.2.4 分析结果比较

不论是线性屈曲分析，还是非线性屈曲分析，得到的结果都是无塔架门塔架的第一阶屈曲载荷值大于有塔架门塔架的第一阶屈曲载荷值，塔架门会降低塔架的屈曲临界载荷值，即降低同种工况下塔架抵抗屈曲失稳的能力，需特别关注塔架门附近的应力并考虑门框加强设计。

塔架稳定性取决于其一阶屈曲临界载荷，塔顶端的叶轮和机舱的总重力为1.18 MN，极限工况下的轴向压力为1.056 2 MN，合力为2.236 2 MN。取经典ANSYS有塔架门的非线性屈曲结果为例，屈曲因子为非线性屈曲特征值与合力的比，约为20，根据IEC标准，对曲线外形件的综合弯曲，如管状塔架和叶片，屈曲因子大于1.2就不会发生屈曲失稳。该塔架的稳定性满足设计要求，不会发生屈曲失稳。

3 结论

本文采用有限元ANSYS软件的非线性屈曲分析方法，对2MW78m风力机薄壁塔架进行了有限元屈曲分析，研究风力机在轴向压力作用下的塔架门对塔架屈曲的影响。塔架门的存在会降低塔架屈曲特征值，降低同种工况下塔架抵抗屈曲失稳的能力。有塔架门塔架的最大应力点出现在塔架门附近，应力最大位置是发生屈曲失稳的危险点，需进行强度校核，但强度不满足设计要求，的考虑门框加强设计。

［1］ 朱仁胜，刘永梅，蒋东翔，等.基于MW级风力发电机塔架的有限元分析［J］.机械设计与制造，2011，5（5）：104-106.

［2］ 高耀东，宿福存，李震，等.ANSYS Workbench机械工程应用精华30例［M］.北京：电子工业出版社，2013.

［3］ 赵世林，李德源，黄小华.风力机塔架在偏心载荷作用下的屈曲分析［J］.太阳能学报，2010（7）：901-906.

［4］ 黄国良，严峰.基于有限元法的框架式压缩机基础动力分析［J］.风机技术，2011（3）：15-19.

［5］ 王慧慧，黄方林，吴合良，等.风力发电机塔架的有限元分析［J］.山东交通学院学报，2009（6）：63-67.

［6］ 王新敏，李义强，许宏伟.ANSYS结构分析单元与应用［M］.北京：北京人民交通出版社，2012.

［7］ Germanischer Lloyd Windengergie GmbH.Guideline for the certification of wind turbines［S］.

［8］ International Electrotechnical Commission.International Standard IEC 61400-1-2005 Wind Turbines［S］.

［9］ 汤炜梁，袁奇.大型风力机塔筒三维有限元分析［J］.电力技术，2010（5）：59-63.