基于模糊聚类的车辆器材周转量品种优化研究
2015-05-07王凤忠吕亚飞李志威邹饶邦彦
王凤忠,吕亚飞,李志威,邹饶邦彦
(1.军事交通学院 军用车辆系,天津 300161;2.军事交通学院 研究生管理大队,天津 300161)
1 引言
2 模糊聚类分析的步骤
2.1 数据标准化
将所研究的论域分为n个对象,每一对象又包含m个指标,由此可初步建立数据矩阵;为使各不同量纲的数据可相互比较,将数据通过变换压缩至[0,1]区间上,即所说的标准化;常用的几种变换方法有平移标准差变换、平移极差变换和对数变换。
2.2 标定
标定即依据各对象间的相似程度建立模糊相似矩阵rij=R(xi,xj)。确定相似矩阵的方法主要有数量积法、夹角余弦法、最大最小法、相关系数法、距离法、主观评分法等方法。
2.3 聚类分析
聚类分析主要有三种方法,分别为:直接聚类法、最大树法和构造模糊等价矩阵法。本文采用构造模糊等价矩阵方法,将所得到得相似矩阵通过传递闭包法得到具备传递性的等价矩阵R*,再将λ由大到小变化,即可形成动态聚类图。
3 评价指标体系的建立
评价指标体系的建立是考察评价对象的基础,指标应能从多方面、多维度深刻描述评价对象。一般而言,确立的目标数量越多,评价效果就越好、越准确;但确定指标权重就越复杂,建模越困难。所以,在建立评价指标体系时,不能盲目扩大指标范围,尽可能做到科学合理、符合实际。通过对车辆器材周转量品种的相关影响因素分析,遵循指标建立的相关原则,建立两级指标体系,见表1。
4 指标权重的确定
为了使评价工作的实现主次有别,能够准确把握评价中的关键,给各指标赋予相应的权重,通过定量的方式确定各项指标在目标评价中所起的作用。各指标对评价目标的贡献不同,则权重就不同,重要者赋予的权重就大,次要者赋予的权重就小。
层次分析法是处理指标难以量化的有效方法,通过将复杂的问题分解成层次结构,然后在更简单的层次上进行分析。
首先,构造比较判断矩阵,确定单层次指标间的相对权重。通过专家评分,对各指标进行两两对比,比较每一个指标对目标的影响程度,以确定它们在目标层中的比重,每次取两个指标对目标的影响程度之比作为比较标度,将全部比较结果进行比较归纳,形成比较矩阵。常采用1-9比较标度方法,见表2。
回顾性分析2015年9月—2018年8月我院58例患者的肋骨骨折CT影像和临床内固定术后病历资料。其中男40例,女18例,年龄20~62岁,平均41岁。单侧肋骨骨折31例,双侧多发多段肋骨骨折27例,肋骨骨折数1~8根,胸壁塌陷6例,胸壁软化3例,合并血气胸5例,肺挫伤23例,呼吸困难6例。
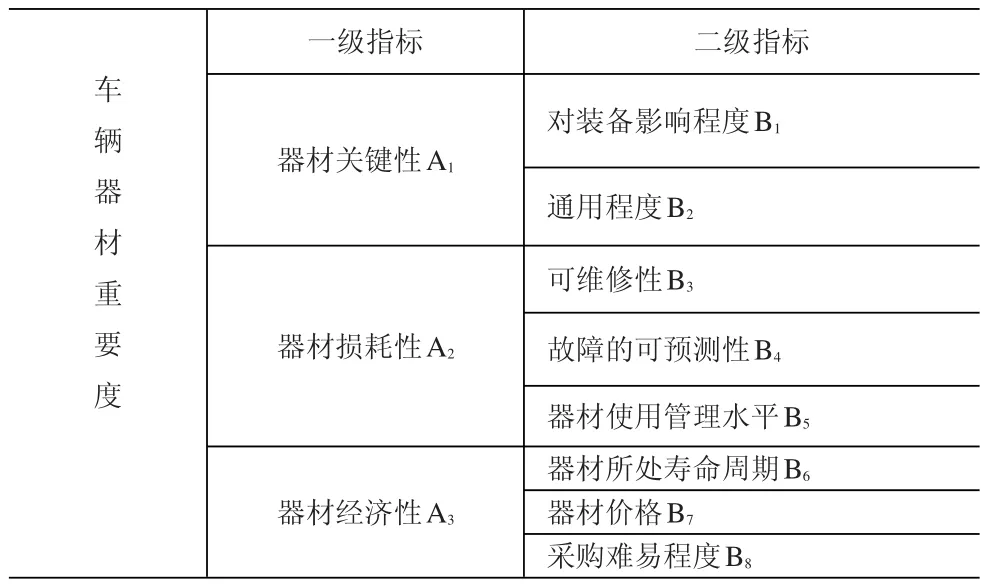
表1 车辆器材周转量品种的相关影响因素重要度评价指标体系

表2 1-9标度表
首先通过专家打分对A1、A2、A3第一级指标构造相对于目标层的权重判断矩阵Z-A,见表3。
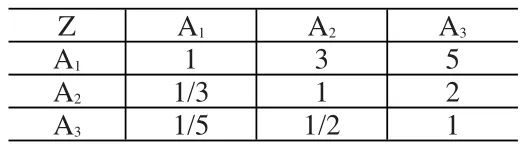
表3 第一级指标打分结果
对所得的三维矩阵的每一行bi的几何平均值的求解
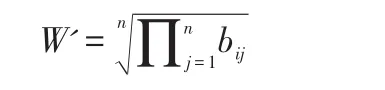
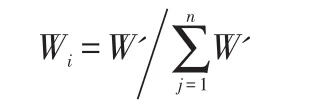
得到各指标的相应权重W=(W1,W2,...,Wn),表3中所求得的相应权重依次为(0.648 3,0.229 7,0.122 0)。
然后,对所求到的权重进行一致性检验,以保证权重的合理性,要计算它的一致性指标C.I,所用公式为:

然后将每一行的wi进行归一化处理,公式为:
其中,λmax为最大特征值,n为判断矩阵的阶数。
此外,还需要对判断矩阵的平均随机一致性指标R.I进行检验,表4给出了1~10阶的平均随机一致性检验指标值。

表4 平均随机一致性检验指标
当满足C.R=0.1时,认为判断矩阵满足一致性。

所以,符合一致性要求,一级指标层A1、A2、A3相对于目标层Z的权重WZ=(0.628 3,0.229 7,0.122 0)。
同理,构建A1—B、A2—B和A3—B,并进行相应地一致性检验,得到相应的权重分别为WA1=(0.75,0.25),WA2=(0.604 4,0.325 5,0.070 1),WA3=(0.111 1,0.666 7,0.222 2)。
最后,利用层次结构中所有层次指标间相对权重的结果,计算最底层指标针对目标层Z的重要性的权值。经一致性检验,第二层指标相对于总目标Z的综合权重为:
WZB=(0.486 2,0.162 1,0.138 8,0.074 8,0.016 1,0.013 6,0.081 3,0.027 1)
5 指标评分
为实现定性指标的量化,明确各评价指标的重要性程度划分,采用四个等级评判标准。即由10名专家组成的评价小组依据器材重要程度确定四个评价等级,分别为I,II,III,IV,相应评语集E={重要,较重要,一般重要,不重要},并赋予每个评语一定的分数,得到评价等级向量G=(9,7,5,3),结合部队车辆周转器材储备实际,将器材重要度划分为四个不同的等级。然后,由10名专家对每一种器材的每一个评价指标进行投票。本文选取某一车型的10种器材为例,对这十种器材的重要程度进行聚类分析。其中,对X1器材的各指标投票结果见表5。
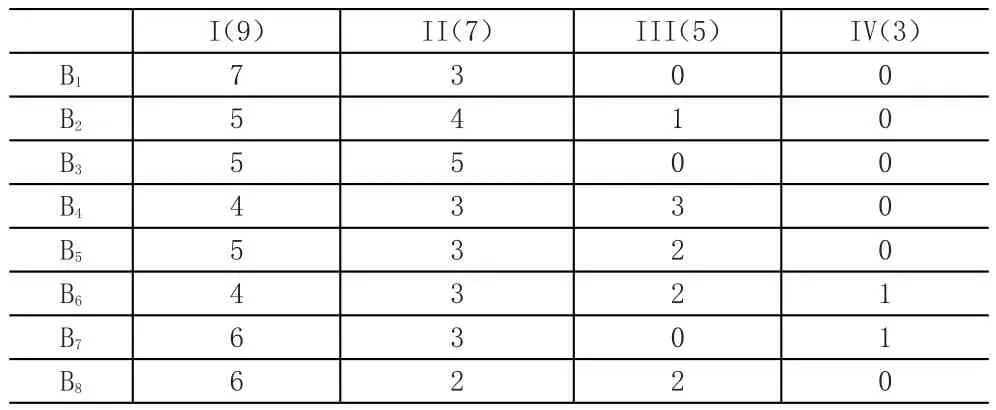
表5 X1的各指标投票结果
则其最终得分为:

以此类推,可得出各器材的各指标得分,为设置对照,增添一列X11,其各指标得分数据为每一行的最大值,见表6。
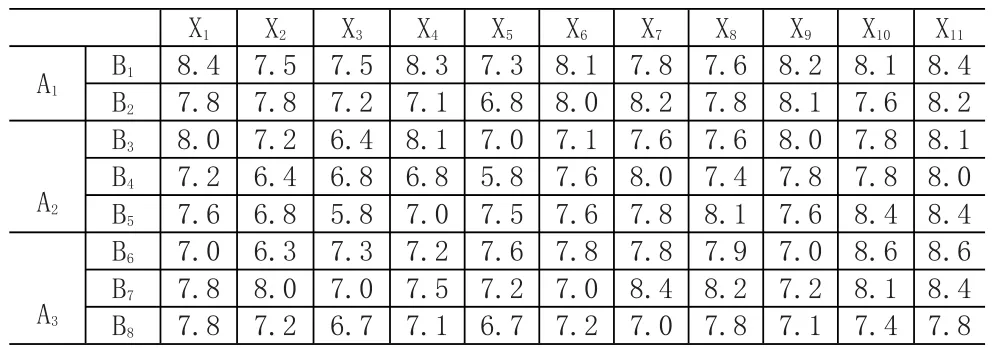
表6 各器材的指标得分结果
6 模糊分析
将以上所得到的打分数据按照前文所述步骤进行模糊分析,本文主要在MATLAB中实现数据的处理和分析。数据标准化过程中,采用的是平移极差变换的方法,建立模糊相似矩阵时采用的是最大最小法,所得到的标准化矩阵和模糊矩阵如下。
标准化矩阵:
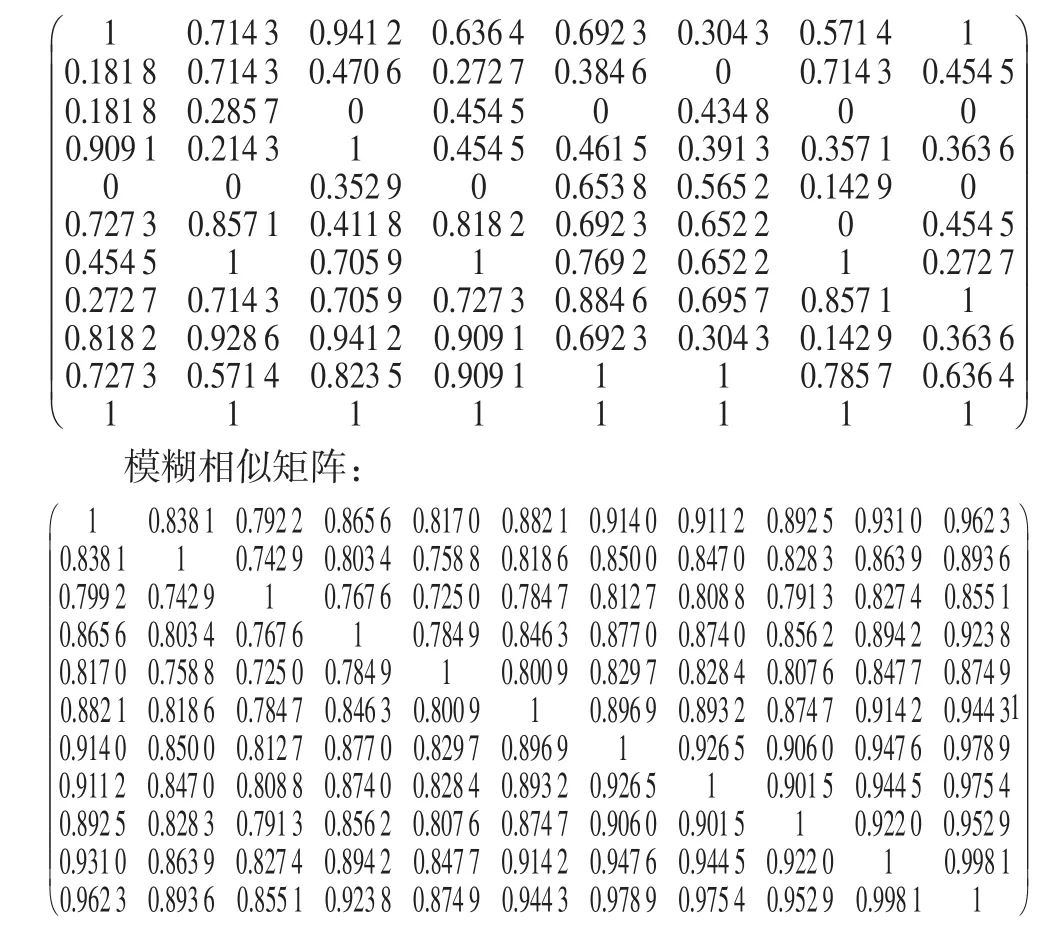
最后通过传递闭包求得等价矩阵,生成动态聚类图。
当λ取值为0.998 1时,可将器材分为10类,其中X10和X11为一类,其余各器材分别为一类,由此可知X10的重要程度和X11最为接近,即重要程度最高;
当λ取值为0.978 9时,共可分为9类,X7、X10和X11为一类,其余各器材为一类;
当λ取值为0.975 4时,共可分为8类,X7、X8、X10和 X11为一类,其余各器材为一类;以此类推。我们可以通过确定最佳阈值λ来确定和X11一类的器材作为筹措的重点器材,由此可确定周转量的器材品种。
7 总结
本文将模糊聚类的方法引入到周转器材的品种优化中,通过MATLAB软件定量确定出器材的品种。经验证方法和理论正确,结果符合实际,考虑到传统ABC分类存在的不足,该方法对确定周转器材品种具有一定的指导作用。
[1]赵复涛.军用车辆器材周转量[D].天津:军事交通学院,2012.
[2]谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社,2013.
[3]张地,刘世通.多层模糊聚类法在军队物资供应商选择中的应用[J].军事交通学院学报,2014,16(2):68-72.
[4]郑俊.改进的灰色聚类法在单层工业厂房可靠性鉴定中的应用研究[D].南昌:华东交通大学,2007.
