基于灰色残差GM(1,1)模型理论的矿井涌水量预测

高 轲 李树文

(1.中国建筑第七工程局有限公司，河南 郑州 450000； 2.河北工程大学城市建设学院，河北 邯郸 056038)

·绿色环保·建筑节能·

基于灰色残差GM(1,1)模型理论的矿井涌水量预测

高 轲1李树文2

(1.中国建筑第七工程局有限公司，河南 郑州 450000； 2.河北工程大学城市建设学院，河北 邯郸 056038)

采用灰色系统预测理论，选取梧桐庄矿历年涌水量实测数据为样本数据，建立了残差GM(1,1)模型，并用相关计算方法对历年涌水数据进行统计计算，得出拟合数据，与实测结果进行比较同时建立修正模型，最终确定其为预测矿井涌水量的合适模型。

涌水量，煤矿，突水，模型

矿井涌水量的大小直接影响到井下排水能力的设计，因此为了保证矿井的安全生产，必须对矿井的涌水量进行科学的预测。煤矿矿井的涌水主要受到地质构造、煤层顶底板的岩性及其组合构造、采动矿压对煤层底板的扰动作用、岩层的富水性、含水层的水头压力及地应力等的影响[1]。在整个系统中存在着一定的不确定性与未知性，所以整个系统呈现出一种“灰”性[2]。因此，可以用灰色理论来探讨矿井涌水量的问题。关于矿井涌水量的预测方法有很多种[3-8]，鲍道亮等运用GM(1,1)模型对苏二煤矿的涌水量进行了动态预测[9]；肖云等针对矿区复杂的水文地质条件，通过建立灰色GM(1,1)预测模型，对铜绿山的未来涌水量变化趋势进行了预测[10]。关于该类问题的研究学者还有很多，如高志扬，钱家忠，张国斌，肖有才等[11-14]。上述研究把GM(1,1)模型应用在矿井涌水量的预测中，但是对模型的优化与修正方面的研究还不够深入。在此背景下，这里介绍一种残差GM(1,1)理论的预测模型。

1 GM(1,1)模型理论及其求解方法[15]

设:

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(2)

则:

x(0)(k)+ax(1)(k)=b

(3)

式(3)为GM(1,1)模型的原始形式。

设:

Z(1)=(z(1)(1),z(1)(2),…,z(1)(n))

(4)

其中:

(5)

式(5)为GM(1,1)的基本形式。

设X(0)为非负序列:

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(6)

其中,x(0)(k)≥0(k=1,2,…,n)；X(1)为X(0)的1—AGO序列。

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(7)

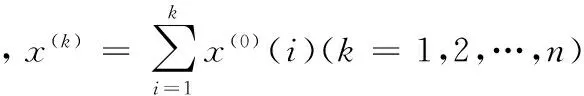
Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

(8)

其中：

(9)

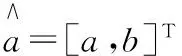
(10)

则GM(1,1)模型x(0)(k)+az(1)(k)=b的最小二乘估计参数列满足:

(11)

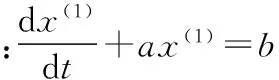
(12)

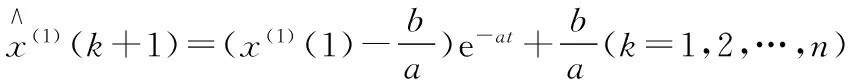
(13)

其中，a为发展系数；b为灰色作用量。

设ε(0)=(ε(0)(1),ε(0)(2),…，ε(0)(n))为X(0)的残差序列，则按前面所述的GM(1,1)建模方法可以得出残差的模拟序列为：

(14)

则相应的残差修正时间响应式为:

(15)

上述式子即为残差GM(1,1)模型。

2 实例分析

这里我们选取梧桐庄矿1998年—2002年的涌水资料为依据，来进行算例分析，其历年涌水量如表1所示。

表1 梧桐庄矿历年矿井平均涌水量

1)据上面所述的计算方法对X(0)作1—AGO序列可得：

X(1)=(x(1)(1),x(1)(2),x(1)(3),x(1)(4),x(1)(5))=
(4.92,8.89,15.96,25.41,43.51)。

2)对X(1)作紧邻均值生成。

令：

得:

Z(1)=(z(1)(2),z(1)(3),z(1)(4),z(1)(5))=
(4.445,12.425,20.685,34.46)。

于是:

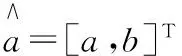
3)确定模型：

其时间响应式为：

4)求X(1)的模拟值：

5)还原求出X(0)的模拟值。

由：

得：

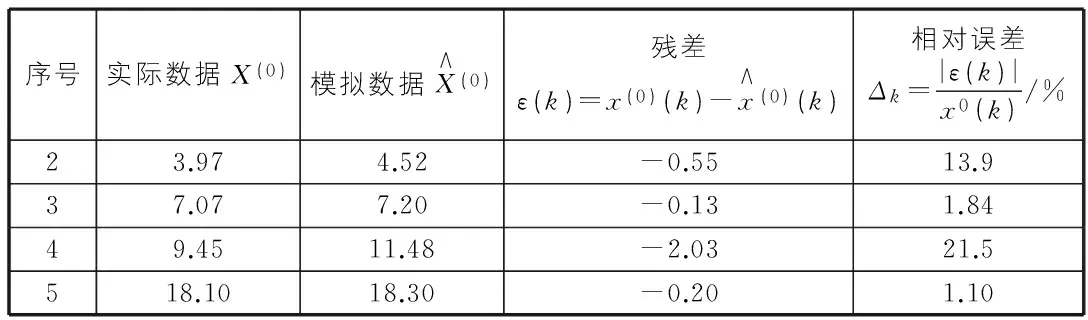
表2 误差检验表

6)检验误差，由表2可以算出残差的平方和:

平均相对误差为：

7)取得残差段为:

ε(0)=(ε(0)(2),ε(0)(3),ε(0)(4),ε(0)(5))=
(-0.55,-0.13,-2.03,-0.20)。

此为可建模残差段，取绝对值得：

ε(0)=(0.55,0.13,2.03,0.20)。

8)建立GM(1,1)模型，得ε(0)的1—AGO序列ε(1)的时间响应式为：

其导数还原值为：

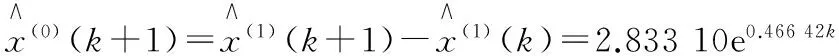
按此模型对表2中的模拟数据进行修正，修正后的精度如表3所示。

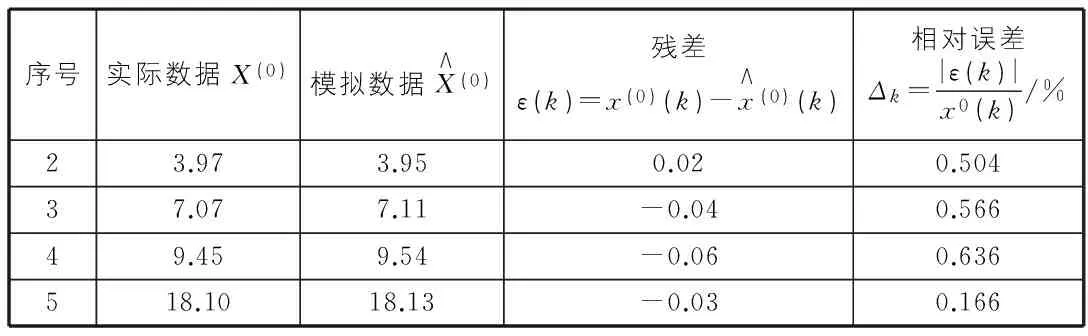
表3 残差GM(1,1)模拟误差

由表3可以算出残差的平方和:

s=εTε=0.006 5。

平均相对误差为：

3 结语

由上述可知，该模型的精度为98.128%，比残差修正之前的精度提高了7.718%。说明该残差GM(1,1)模型具有更高的精度，可以达到我们所需要的精度要求，并且该残差GM(1,1)模型可以用于指导矿井涌水量的预测。为以后合理制定矿井突水对策以及合理布置井下排水设施提供了一定的依据。

[1] 虎维岳.矿山水害防治理论与方法[M].北京:煤炭工业出版社,2005:50-99.

[2] Deng Ju Long.Grey System Basic Method[M].Wuhan:HUST press,2005.

[3] 王金国,江洪清,高永奎.基于Matlab的矿井涌水量神经网络预测方法及应用[J].煤炭科技,2004,23(7):67-68.

[4] 李树文,侯双林,王 龙.矿井涌水量预测的灰色数值模型研究[J].科技情报开发与经济,2007(4):191-193.

[5] 陈崇希,陈明佑,陈爱光.矿坑涌水量计算方法研究[M].武汉：武汉地质学院出版社,1985.

[6] 刘永峰.平煤股份朝川矿—井涌水量预算方法研究[J].能源技术与管理,2011(3):89-91.

[7] 温文富,曹丽文.比拟法和解析法在某矿井涌水量预测中的分析比较[J].中国煤炭,2011(7):45-47.

[8] 郑华萍.应用综合分析法分析矿井涌水量[J].西安矿业学院学报,1997,17(2):150-154.

[9] 鲍道亮,刘宏锦.基于GM(1,1)模型的矿井涌水量预测[J].龙岩学院学报,2010,28(2)：99-100.

[10] 肖 云,田昌贵,李云松.基于GM(1,1)模型的铜绿山矿井水害预测与防治[J].安全与环境工程,2013,20(1):115-119.

[11] 高志扬,徐 杰.基于优化GM(1,1)模型的矿井涌水量预测及算法实现[J].矿业安全与环保,2013,40(1):74-88.

[12] 钱家忠,朱学愚,吴剑锋.矿井涌水量的灰色马尔可夫预报模型[J].煤炭学报,2000,25(1):71-75.

[13] 张国斌,张建新.新疆有色集团天池矿业公司大平滩煤矿涌水量的GM(1,1)模型预测[J].新疆有色金属,2010(6):21-24.[14] 肖有才,张秀成,王宏艳.灰色理论在预测深埋型矿井涌水量中的应用[J].辽宁工程技术大学学报,2004,23(2):176-177.

[15] 刘思峰,党耀国.灰色系统理论及其应用[M].北京:科学出版社,2010:146-161.

The mine water inflow prediction based on grey residual GM(1,1) model theory

Gao Ke1Li Shuwen2

(1.ChinaBuilding7thEngineeringBureauLimitedCompany,Zhengzhou450000,China;2.CollegeofUrbanConstruction,HebeiEngineeringUniversity,Handan056038,China)

Using grey system prediction theory, this paper selected the bygone years water inflow measured data of Wutongzhuang mine as the sample data, established the residual GM(1,1) model, and made statistical calculations to bygone years water inflow data using related calculation method, concluded that the fitting data, and comparing with the measured results, established at the same time the correction model, ultimately determined the appropriate model for prediction mine water inflow.

water inflow, coal mine, water inrush, model

1009-6825(2015)28-0174-03

2015-07-25

高 轲(1987- )，男，硕士，助理工程师

P641

A