六维力/力矩传感器静态解耦算法的研究与应用*

2015-05-06宋爱国徐国政

传感技术学报 2015年2期

关键词：静态标定力矩

茅晨,宋爱国,高翔,徐国政

(1.南京邮电大学自动化学院,南京 210023;2.东南大学仪器科学与工程学院,南京 210096)

六维力/力矩传感器静态解耦算法的研究与应用*

茅晨1*,宋爱国2,高翔1,徐国政1

(1.南京邮电大学自动化学院,南京 210023;2.东南大学仪器科学与工程学院,南京 210096)

维间耦合是影响多维力/力矩传感器测量精度的一个主要因素。介绍了六维力/力矩传感器维间耦合的基本原理,在研究基于求解矩阵广义逆的静态解耦算法的基础上,提出了基于耦合误差建模的静态解耦算法。以实验室研制的六维力/力矩传感器为例进行标定实验,用两种解耦算法对其进行解耦计算。实验结果证明基于耦合误差建模的静态解耦算法的有效性。

维间耦合;六维力/力矩传感器;耦合误差模型;静态解耦算法

多维力/力矩传感器安装于机器人手臂和手爪之间,用于检测机器人手在操作时与所处环境的作用力/力矩的大小及方向,并反馈给机器人力控制系统,是机械臂实现力控制的信息获取装置[1-2]。由于受结构设计原理、机械加工精度、应变片组桥方式以及传感器标定方式等影响,多维力/力矩传感器的各路输出信号间存在耦合误差。如何通过解耦算法的计算最大可能地减小耦合误差是研究多维力/力矩传感器的关键性技术[3]。

本文以实验室研制的六维力/力矩传感器为依托,首先利用传统的基于标定矩阵的求解矩阵广义逆的静态解耦算法进行解耦,随后提出了基于耦合误差建模的静态解耦算法,并对两种解耦算法进行了误差分析比较,判断其优劣性。

1 耦合误差的提出

理想的六维力/力矩传感器,每一方向输出通道的电压值仅取决于该方向作用力/力矩的大小,与其余五方向作用力/力矩大小无关。但是由于传感器的结构设计、机械加工的精度、贴片技术、应变片横向效应与检测方式等方面的原因[4],几乎每一维作用到传感器上的力/力矩分量都会对传感器的各路输出信号产生影响,这就是维间耦合[5]。

表1是我们对六维力/力矩传感器进行标定实验时记录的一组数据。表中Force的单位为N,各方向的电压值单位为V。从表1中可以看出,Fx方向的电压输出值随着X负方向加载的标准力值的变化而变化,且大致是成线性变化的;但是同时其他5个方向的电压输出值也有变化,特别是My方向的电压输出值变化较大,也就是说X方向施加的作用力对其他5个方向的测量也产生了影响。由此可见,维间耦合是影响多维力/力矩传感器测量精度的一个主要因素。

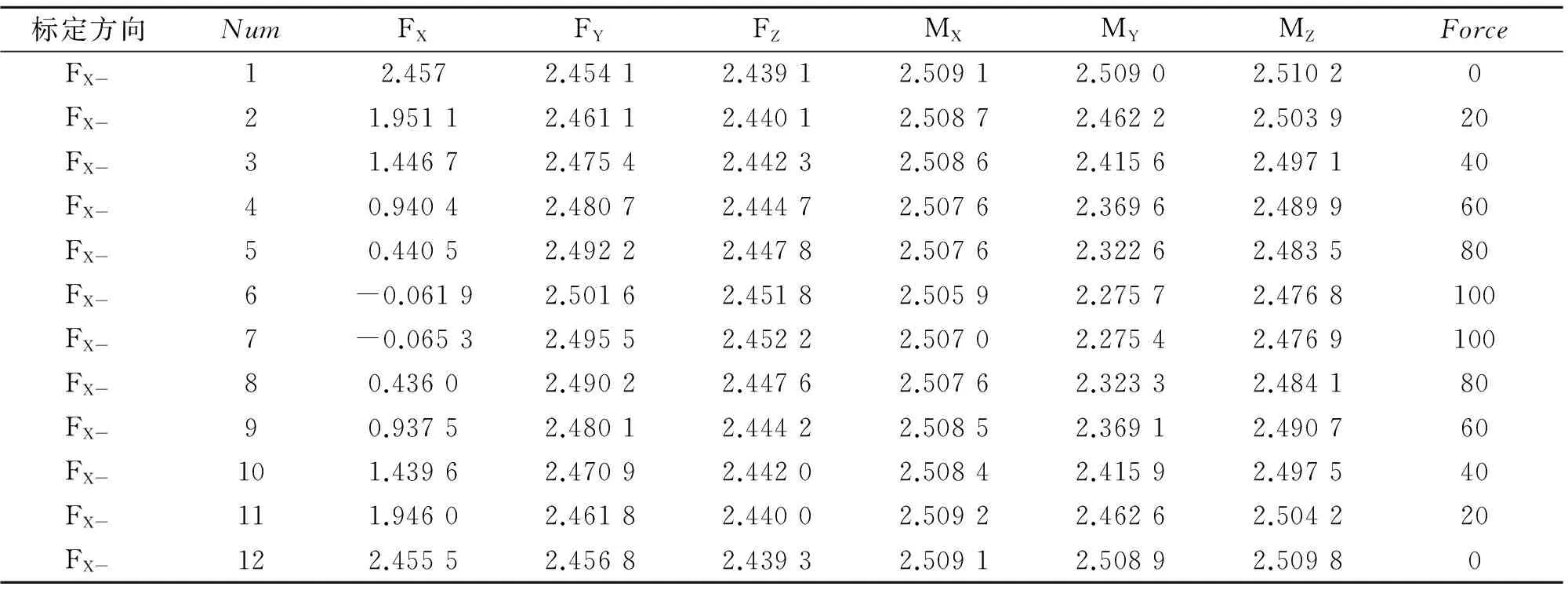
表1 X负方向力值标定实验记录

通常多维力/力矩传感器的解耦有两种方法。一种是硬件解耦,即从结构设计、机械制造工艺等方面入手,从根源上着手消除耦合,但是这种方法涉及复杂的工艺技术问题,难以实现,且大大增加了传感器的制造成本;另一种方法是软件解耦,具有可操作性强、解耦速度快、精度高等优点。

本文采用砝码重锤式静态标定方法,其标定装置为本实验室自行研制的加载实验台[6]。

2 基于求解矩阵广义逆的静态解耦算法

首先,做如下假定[7]:①任何输入的作用力都能够分解为三维空间坐标系中的3个力分量Fx、Fy、Fz和3个力矩分量Mx、My、Mz;②输出电压向量对应整个传感器的输出空间,并且在传感器载荷范围内主方向的输入与输出之间是线性关系;③输出电压可以进行线性叠加。

这里用力向量(Fx,Fy,Fz,Mx,My,Mz)T来表示任意一个作用力,用(UFx,UFy,UFz,UMx,UMy,UMz)T来表示传感器在一个作用力下的六路电压信号输出,力向量和输出电压向量关系见式:

(1)

利用实验室的标定装置,对六维力/力矩传感器进行标定实验,对其施加三维空间6个线性独立的标准力/力矩分量,并对应记录下传感器输出的六路电压向量,按序构成矩阵,从而建立矩阵式[8]:

U=HF

(2)

式中,F为6×n力分量矩阵(n为总共的标定实验次数);U为6×n电压向量矩阵;H为6×6常数矩阵。由求解矩阵方程最小二乘估计量的方法求得常数矩阵:

H=U(FTF)-1FT

(3)

在对传感器进行解耦时,自变量为传感器输出的6个电压向量,而作用在传感器上的六维力/力矩分量是未知的,其关系式可用式(4)表示:

F=CU

(4)

联列式(2)与式(4)可求得:

C=(HTH)-1HT

(5)

C即为标定矩阵,又叫解耦矩阵,是一个6×6的矩阵。对传感器进行标定工作就是为了确定标定矩阵C。求解标定矩阵C的过程实际上就是多元函数最小二乘拟合的过程[9]。为了获得较为准确的标定矩阵,要求标定的实验次数要远大于六维力/力矩传感器的维数。

根据多次标定实验记录的数据,利用MATLAB计算得到标定矩阵C为:

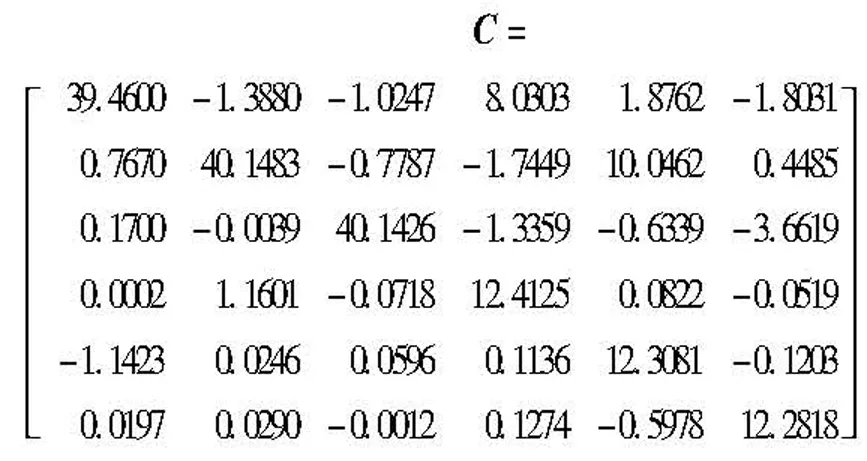
(6)

基于标定矩阵的求解矩阵广义逆的静态解耦算法,虽然原理简单,但其涉及到众多矩阵运算,算法推导复杂,运算量大,且容易产生病态矩阵,会导致解耦精度降低甚至导致解耦结果错误[10]。

3 基于耦合误差建模的静态解耦算法

首先,假设六维力/力矩传感器在载荷范围内不存在维间耦合,即各个方向的电压输出值仅与该方向施加的力/力矩分量值有关,如图1所示。

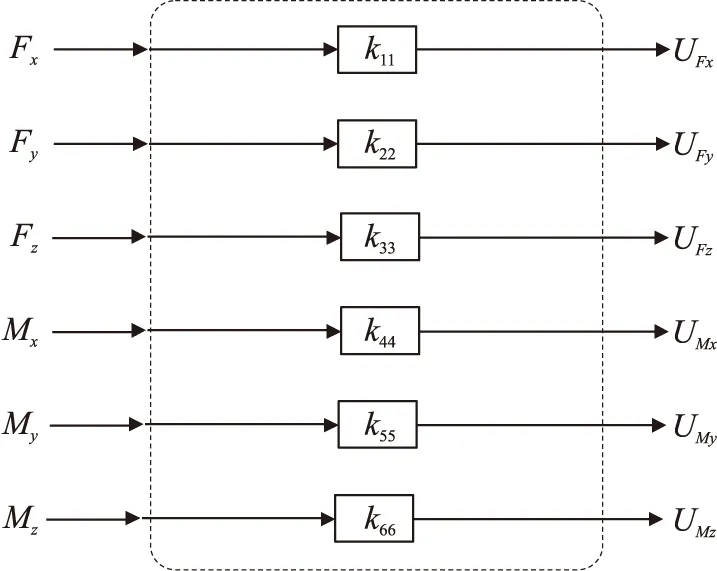
图1 无耦合时六维力/力矩传感器输入输出系统

该关系可用表达式(7)表示:

(7)

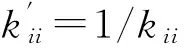
(8)

在实际情况下,六维力/力矩传感器存在较大的维间耦合。为描述方便,这里我们假设维间耦合成一元线性关系,如图2中所示,每一个通道的电压输出值由六路作用力/力矩分量叠加而成,亦可写成表达式(9)。

(9)

其中,Uii为主方向作用力/力矩对该方向电压通道输出值的影响分量,Uij(i≠j)为其他5个耦合方向施加作用力/力矩时对该方向电压通道输出值的影响分量(即j方向对i方向的耦合)。

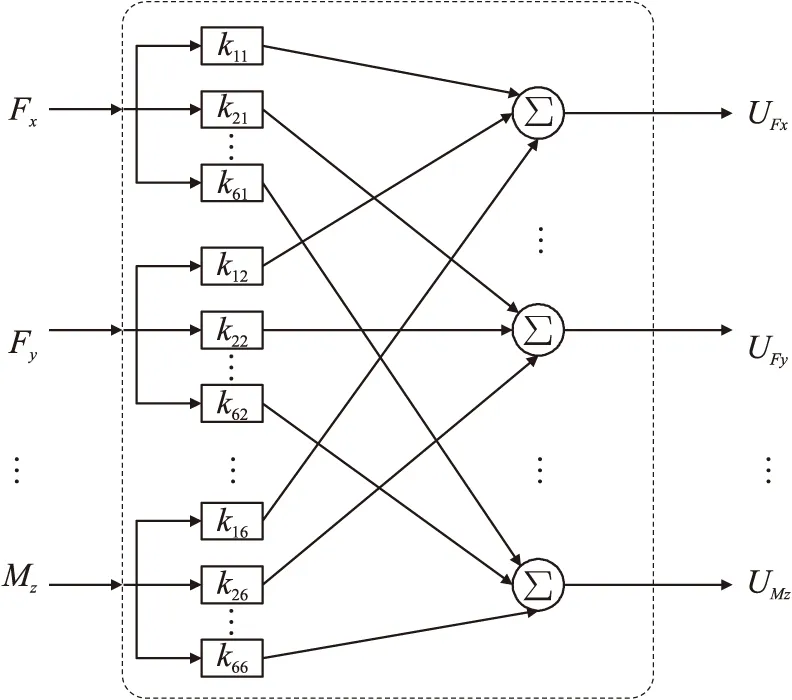
图2 有耦合时六维力/力矩传感器输入输出系统

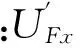
(10)

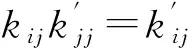
(11)

同理,我们可以推导其他5个方向的解耦公式,得到解耦方程组(12):

(12)

方程组(12)即为本文提出的基于耦合误差建模的静态解耦算法的基本模型。该模型是在耦合误差为一元线性的前提下得到的[11]。在实际应用时可结合具体情况,用二阶、三阶……来代替模型中的耦合误差。

根据实验室大量的传感器标定数据分析,维间耦合复杂多样,并不是简单地成线性关系,并且同一标定方向的正负方向的标定数据也有差异。综合计算复杂度与精度考虑,在处理耦合数据时采用分段二阶拟合方法。

对Fx方向施加标准力,记录下6个通道的电压输出值UFx、UFy、UFz、UMx、UMy以及UMz,对主方向采用一元线性回归方程拟合,耦合方向采用分段二阶拟合:

(13)

拟合曲线图如图3所示。

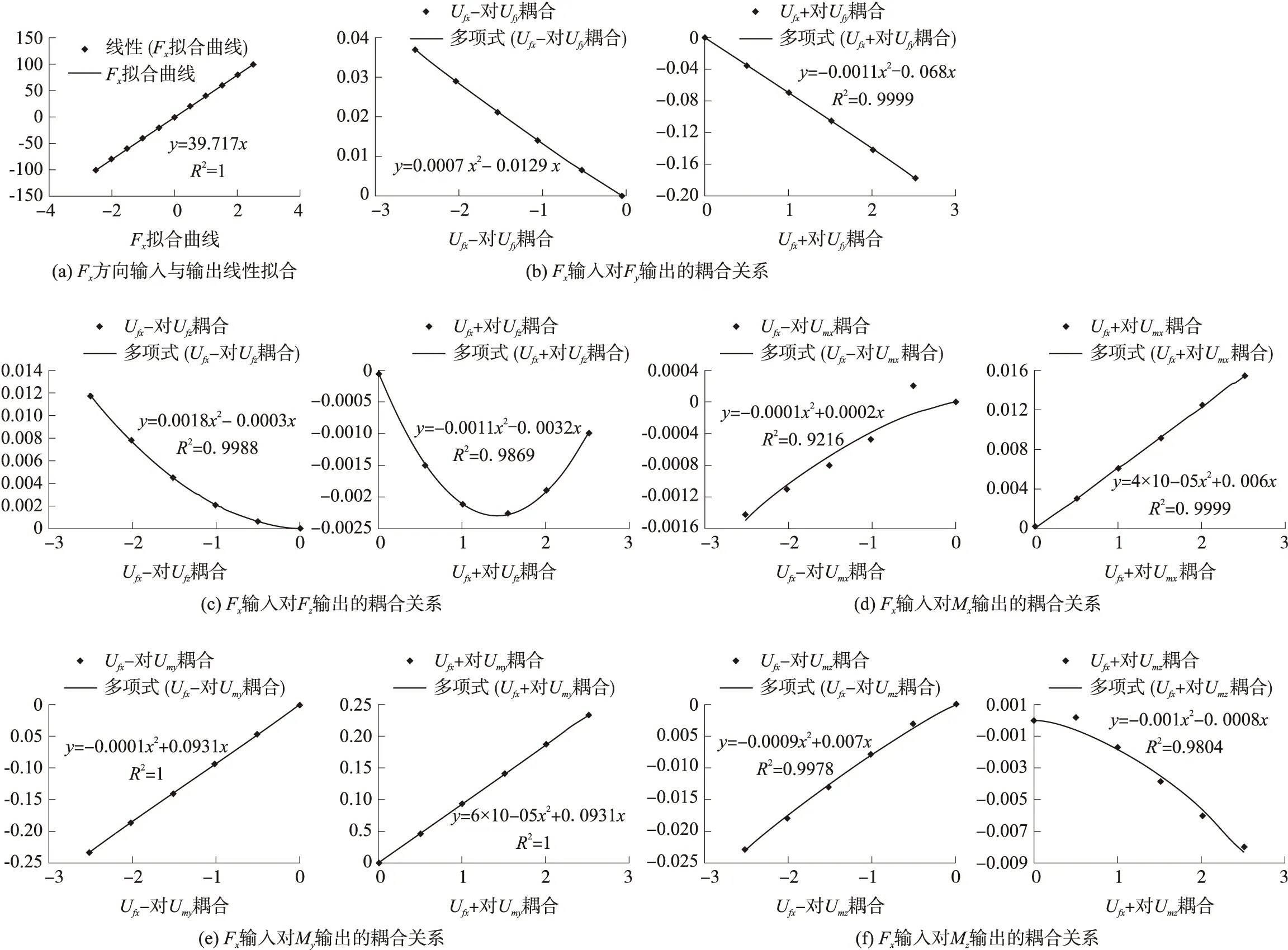
图3 Fx方向拟合曲线

对Fy、Fz、Mx、My以及Mz方向标定实验得到的数据的处理方法与Fx方向类似。最后将求得的系数代入,得到解耦公式为:

Fx=39.717(UFx-CFy_Fx-CFz_Fx-CMx_Fx-CMy_Fx-CMz_Fx)

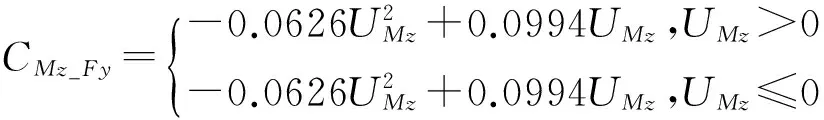
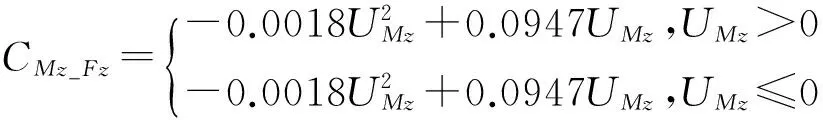
My=12.363(UMy-CFx_My-CFy_My-CFz_My-

CMx_My-CMz_My)

4 误差分析与比较

六维力/力矩传感器是一个测量力/力矩值的传感器,为了综合评价一个传感器的优劣程度,需要对传感器的测量值有一个精度指标。我们用综合误差(或Ⅰ类误差)[12]和耦合误差(或Ⅱ类误差)[13]来表示:

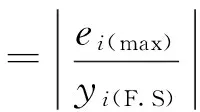
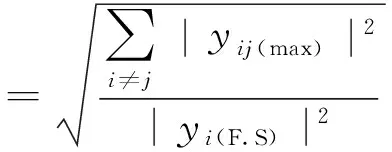
其中yi(F.S)表示i方向可施加力(或力矩)的满量程值;ei(max)表示i方向实际施加的标准力(或力矩)值与真实测得的力(或力矩)值之差的最大值;yij(max)表示当j方向施加力(或扭矩)值、其他5个方向无力(或扭矩)作用时,i方向测得的最大力(或扭矩)值。

两种解耦算法的误差分析见表2。

分析表2,由于实验室研制的六维力/力矩传感器对于主方向有着较好的线性度,因此两种解耦算法对Ⅰ类误差的影响不大。

表2 传感器未解偶时以及解耦后的精度对比

经解耦后,各方向的Ⅱ类误差有着显著减少。两种解耦算法在一定程度上都能减小维间耦合的干扰,但是基于标定矩阵的求解矩阵广义逆的静态解耦算法的解耦效果不理想,解耦效果时好时坏,且容易产生病态矩阵。综合来看,基于耦合误差建模的二阶分段拟合的静态解耦算法较为稳定,能有效抑制各维维间耦合的干扰,提高传感器的精度。

5 结论

文章研究了基于标定矩阵的求解矩阵广义逆的静态解耦算法和基于耦合误差建模的静态解耦算法,并基于实验室研制的六维力/力矩传感器进行了解耦计算。结果表明,基于耦合误差建模的静态解耦算法简单可靠,且能反应多维力/力矩传感器维间耦合的本质。

[1] 张福学.机器人学-智能机器人传感技术[M].北京:电子工业出版社,1996.

[2]Lee S,Asada H.A Perturbation/Correlation Method for Force Guided Robot Assembly[J].IEEE Trans Robot Autom,1999,15:764-773.

[3]Ma J Q,Song A G.Development of A Novel Two-Axis Force Sensor for Chinese Massage Robot[C]//Zhao QC,ed.Advances in Precision Instrumentation and Measurement.Volume 103.Stafa-Zurich:Trans Tech Publications Ltd,2012:299-304.

[4]武秀秀,宋爱国,王政.六维力传感器静态解耦算法及静态标定的研究[J].传感技术学报,2013,26(6):851-856.

[5]黄心汉.机器人腕力传感器标定矩阵的解[J].电气自动化,1989,10(3):48-50.

[6]茅晨.特殊机器人用六维力/力矩传感器关键技术研究[D].南京:东南大学仪器科学与工程学院,2013.

[7]吴涓.六维腕力传感器的改进及机器人解耦的研究[D].南京:东南大学仪器科学与工程学院,2002.

[8]Song Aiguo,Wu Juan,Qin Gang,et al.A Novel Self-Decoupled Four Degree-of-Freedom Wrist Force/Torque Sensor[J].Measurement,2007,40(Issues 9-10):883-891.

[9]肖汶斌,董文才.六维力传感器静态解耦方法[J].海军工程大学学报,2012,(3):46-51.

[10]马俊青,宋爱国,吴涓.三维力传感器静态解耦算法的研究与应用[J].计量学报,2011,32(6):517-521.

[11]宋爱国,马俊青.基于耦合误差建模的多维力传感器解耦方法[P].Volume 201010168331 2010.

[12]秦岗,曹效英,宋爱国,等.新型四维腕力传感器弹性体的有限元分析[J].传感技术学报,2003,16(3):238-241.

[13]徐科军,李成.多维腕力传感器静态解耦的研究[J].合肥工业大学学报(自然科学版),1999(2):3-8.

Research and Application of Static Decoupling Algorithm for Six-Axis Force/Torque Sensor*

MAOChen1*,SONGAiguo2,GAOXiang1,XUGuozheng1

(1.School of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China;2.School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China)

Static coupling is one of the most important factors affecting the measuring accuracy of multi-axis force/torque sensor.This paper introduces the principle of six-axis force/torque sensor’s couple.The decoupling algorithm based on solving generalized inverse matrix is studied,and a new static decoupling algorithm based on coupling error modeling is proposed.The experimental results on the six-axis force/torque sensor designed by the lab show that the novel algorithm is effective.

static coupling;six-axis force/torque sensor;coupling error modeling;static decoupling algorithm