多轴承支撑轴系的轴承工作游隙优化研究

刘 越, 戈红霞, 望运虎

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

多轴承支撑轴系的轴承工作游隙优化研究

刘 越, 戈红霞, 望运虎

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

根据弹性力学薄壁圆环理论，在充分考虑轴承运转中工作游隙影响因素的基础上，建立轴承内外圈与轴和轴承座过盈配合的计算模型，并考虑轴承工作游隙受到轴承运转过程中内外圈温差膨胀的影响，推导得到过盈配合对轴承工作游隙影响量的计算方法.通过算例表明，多轴承支撑轴系结构中，通过优化各轴承工作游隙，实现轴承的等寿命设计是可行的，并可以工程图的形式用于产品设计中.

轴承；工作游隙；过盈配合；公差

轴承游隙是轴承在无外力作用下，轴承内圈相对于轴承外圈的径向或轴向位移量[1-2].轴承的原始游隙值分为5组，按大小依次为2组、0组、3组、4组和5组.2组游隙最小，5组游隙最大，0组为基本组.

由于轴承内圈一般采用过盈配合，并且在运转过程中存在温升，轴承的实际工作游隙会小于原始游隙.轴承的工作游隙影响支撑的运转精度、轴承之间的载荷分配、轴承内部滚动体载荷分布和滚道接触应力、轴承的支撑刚度和轴承的实际使用寿命,等等.

目前，轴承的研究人员对轴承的热变形和装配造成的游隙减少有了一定的理论研究，但总体系统研究较少[3-4]，采用优化轴承工作游隙，合理分配多支撑轴承受力的研究更为少见.文献[5]针对工程上典型的多轴承支撑轴系结构，提出了一种充分考虑轴承游隙的轴和轴承刚度耦合建模计算方法，可计算多个轴承支撑下轴系结构中各轴承精确载荷分布.文献[6]通过圆柱滚子轴承载荷分布的推导，计算不同径向游隙下轴承各位置滚子的载荷，从而得到轴承内圈和外圈的当量载荷和寿命计算方法.文献[7]从理论上研究了热变形对滚动轴承工作游隙的影响，并研究了装配应力及旋转速度对游隙变化的影响，计算合适的原始游隙.

本研究在多轴承支撑轴系变形耦合计算的基础上，在计算轴承内外圈温差导致轴承工作游隙减少的基础上，通过优化轴承的配合公差，使轴承在运转过程中处于最佳的游隙状态.

1 游 隙

轴承的游隙分为径向游隙和轴向游隙两种，设计人员多按照径向游隙选用轴承[4].轴承游隙过大会造成滚动体与滚道过早出现接触疲劳，使轴承提前失效;轴承负游隙同样也会使滚动体和滚道的接触应力增加，轴承使用寿命低于设计寿命.当运转中出现较大的负游隙时，轴承会由于内外圈温差较大卡死.合理地设计轴承工作游隙，是正确使用轴承的前提条件，也是保证轴承寿命至关重要的因素.

轴承的游隙按照制造、装配和使用可以分为原始游隙Pd、安装游隙Ph和工作游隙Pt.安装游隙是指轴承压配到轴和轴承座后的游隙，如式(1)所示.轴承运转过程中由于摩擦产生的热量会导致轴承内部温度升高，引起轴、轴承座和轴承内外圈的膨胀，轴承内外圈的温差膨胀后的游隙是轴承的工作游隙，如式(2)所示.

Ph=Pd-Δh-Δs.

(1)

式中：Δh是轴承压配到轴承座引起的游隙减少量；Δs是轴承压配到轴上的游隙减少量.

Pt=Ph-Δt.

(2)

式中：Δt是轴承内外圈热膨胀引起的游隙减少量.

2 工作游隙的变化规律

2.1 安装游隙

轴承内外圈与配合轴和轴承座的装配可简化为薄壁圆环模型，如图1所示.轴承内圈单位长度承受的压力为p，内圈内半径为Rii，内圈外半径为Rio，作用在单元上的径向合力如式(3)所示.

(3)

径向单位的单位应变为：

(4)

式中：u是轴承内圈直径方向的变形量，其余参数见图1.

图1 轴承内圈与轴配合的简化模型

根据平面应变理论有

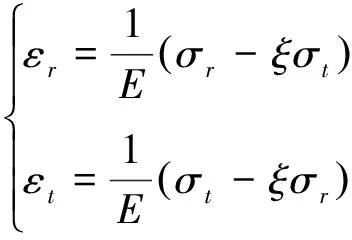
(5)

式中：E是材料的弹性模量，ξ是材料的泊松比.

联立方程(3)～(5)，求得在任意径向位置R，由于内部压力p引起的半径变化量u为：

(6)

设轴承内圈和轴的直径过盈量为I，轴承内圈和轴的材料相同，轴承的内圈游隙减少量为Δs，即：

(7)

式中：Rso是轴承内圈配合轴的半径；Rsi是配合轴的内孔半径.

当内圈配合轴为实心轴时，半径Rsi是零，于是Δs为：

(8)

同样，轴承外圈压装到轴承座时游隙减少量为Δh，即：

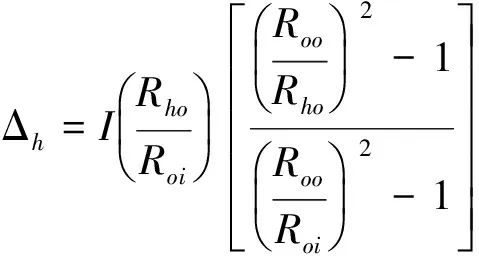
(9)

式中：Roo是轴承外圈外半径；Roi是轴承外圈内半径；Rho是轴承座外半径.

2.2 温差膨胀

根据文献[2]提供的方法，滚动轴承在室温下安装，但工作状态下的轴承在比室温高ΔT的温度下运转，且轴承内外圈存在温差，配合后直径方向的膨胀量Δt为：

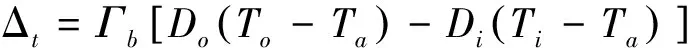
(10)式中，Γb为轴承的线膨胀系数;Do为轴承外圈直径;Di为轴承内圈直径；To为轴承运转中外圈温度；Ti为轴承运转中内圈温度；Ta为轴承装配时室温.

3 案 例

某高功率密度综合传动箱前传动结构，如图2所示.

根据力学分析，驱动轴的载荷作用简化力学模型如图3所示.

图3中，输入扭矩Ti=2 597.7 N·m；泵输入齿

轮作用在驱动轴上载荷Fy1=817.647 N；Fz1=297.599 N；T1=41.7 N·m；输入直齿轮作用在驱动轴上载荷Fy2=-15 100.426 N；Fz2=5 796.134 N；T2=2 204 N·m；转向机构输出扭矩To=352 N·m.

图2 前传动结构方案

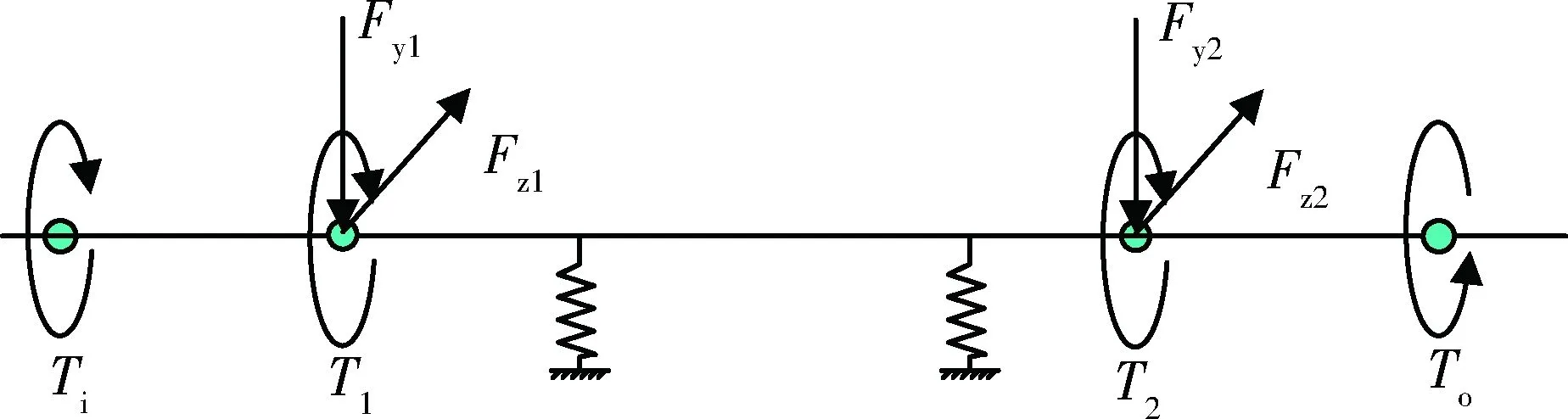
图3 驱动轴受载简化图

在多轴承支撑的轴系分析中，轴承内圈的位移和轴配合节点处的位移是满足变形协调关系的.把轴承单元作为变刚度的弹簧单元，其中一个节点(轴承内圈)与轴配合节点固结，即具有相同的转角和位移.

对图3所示的模型进行轴系力学计算，得到左右轴承的刚度矩阵分别为：

计算得到圆柱滚子轴承的载荷如表1所示.

利用ISO281和ISO16281计算圆柱滚子轴承寿命，如表2所示.

表1 圆柱滚子轴承的载荷

表2 轴承寿命计算

由于前传动为悬臂设计，径向载荷大部分被右轴承承担，其寿命是左轴承的一半，在过载的情况下有可能右轴承最先失效.因此，按照等寿命的设计原则，前传动设计并非最优方案.

如前传动中右轴承改为两个并排安装的轻系列滚柱轴承NU212和NJ212，成为典型的多轴承支撑轴系结构，如图4所示.这种轴承布置结构没有增加轴向空间，但若采用原配合公差尺寸，会出现轴承载荷分配不均的现象.

图4 前传动变动方案图

右边2个轴承选取同样的配合和轴承游隙，会造成轴承1和轴承2载荷分配不均，表3是2个轴承承担的载荷.轴承2承担的载荷是轴承1的2.5倍，因此在润滑情况一致的情况下会最先失效.

表3 圆柱滚子轴承的载荷

按文献[5]提供的多轴承支撑轴系系统变形计算的方法，以轴承承担径向载荷与其额定动载荷比值最小为优化目标，通过对轴承1和轴承2工作游隙的优化，得到：轴承1的最佳工作游隙为0.01 mm，轴承2的最佳工作游隙为0.04 mm，经优化后的载荷大小如表4所示.

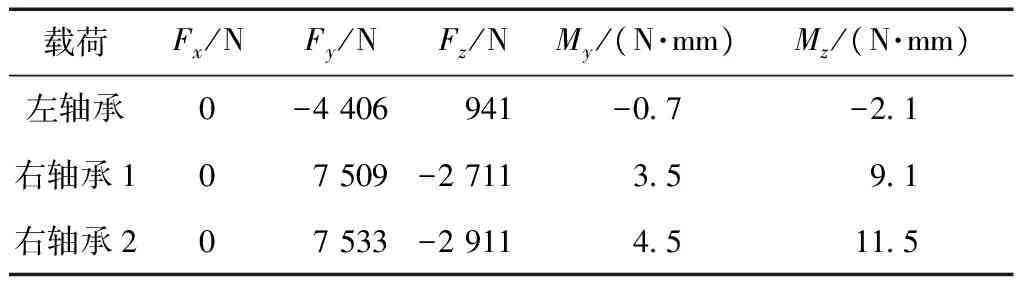
表4 游隙优化后的轴承载荷

轴承钢热膨胀系数为Γ=8.5×10-6mm/mm/℃，轴承NJ(NU)212外圈直径Do=110 mm，内圈直径Di=60 mm，轴承内圈外半径为Do=72.5 mm.装配室温21 ℃，运转时内圈温度为149 ℃，外圈温度为121 ℃.根据式(10)，由于温差膨胀产生的直径方向膨胀量△t为0.028 mm.

通过查找轴承手册，轴承NJ(NU)212的普通组原始游隙为20～45 μm.对于轴承原始游隙和公差配合均取中值，由式(1)、式(2)可得，达到最佳工作游隙时的内圈过盈造成的游隙减少量Δs为：轴承1的Δs为0.05 mm，轴承2的Δs为0.02 mm.由于配合轴为实心轴，由式(8)反求过盈量I，得到轴承1的内圈过盈量I为0.08 mm，轴承2的内圈过盈量I为0.03 mm，取轴承的内圈内直径的平均公差为-0.007 mm，配合轴的直径的公差为：轴承1的配合轴直径公差为+0.073 mm，轴承2的配合轴直径公差为+0.023 mm.

综合考虑轴承的工作游隙、装配游隙和原始游隙后，可确定NU212和NJ212的配合轴径公差，经优化后，在工程图纸中设计轴承配合处的尺寸如图5所示.

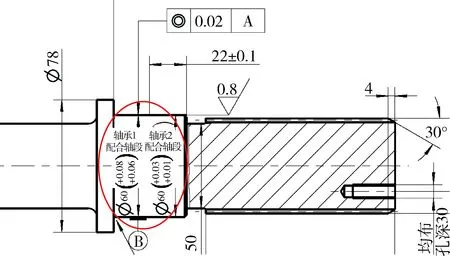
图5 驱动轴与轴承的公差

4 结 论

1)轴承运转中的工作游隙与装配前的原始游隙相差很大，轴承的实际配合公差对轴承的径向游隙产生重要的影响，在轴承的实际运转过程中的游隙受到轴承配合公差、运转时的工作温度等因素的影响.

2)多轴承支撑的轴系结构中，若不对支撑轴承的配合公差进行优化，非但起不到共同承载的作用，且容易产生轴承之间相互作用载荷，导致个别轴承承担超出预计或大多数的工作载荷，出现提前失效的情况.经轴承的配合公差优化后，可均化轴承的受载，实现多轴承的等寿命设计思想.

[1] 刘泽九, 贺士荃, 刘 晖. 滚动轴承应用[M]. 北京: 机械工业出版社,2007

[2] T.A. Harris, Kotzalas. 滚动轴承分析(第1卷)[M].5版.北京:机械工业出版社,2010

[3] 万长森. 滚动轴承的分析方法[M]. 北京: 机械工业出版社,1985.

[4] 刘晓初. 有效过盈量对轴承径向工作游隙的影响[J]. 轴承,1996，(11)：11-16.

[5] 刘 越,周广明,张祖智,等. 多轴承支撑轴系的精确变形计算研究[J]. 兵工学报,2014,35(3):305-311.

[6] 徐淑萍, 马金明. 圆柱滚子轴承游隙与寿命关系[J]. 沈阳理工大学学报,2011,30(4):43-47.

[7] 胡鹏浩,费业泰,黄其圣.滚动轴承最佳工作游隙的确定[J].仪器仪表学报,2002,23(3):33-35.

Research on Bearing Working Clearance ofMulti-bearing Shafting System

LIU Yue, GE Hong-xia, WANG Yun-hu

(Science and Technology on Vehicle Transmission Laboratory, China NorthVehicle Research Institute, Beijing 100072, China)

According to the thin-walled rings in elastic mechanics, the interference fit model of out ring and inner ring is presented for the typical multi-bearing shafting system based on pivotal factors, which includes influence of expanding of outring and innerring temperature difference when the bearing is in operating. The working clearance is calculated in this model. It is proven that the bearing equal life method of optimizing working clearance is feasible, which can be implemented in the blueprint.

bearing; working clearance; interference fit; tolerance

1009-4687(2015)03-0041-04

2014-11-10.

时间：2015-03-20 10 ∶11.

刘越(1987-)，男,工程师，研究方向为传动技术.

TH133.3

A

URL: http://www.cnki.net/kcms/detail/11.4493.TH.20150320.1011.002.html