概率与递推数列的综合应用

河北省石家庄市第二中学 李 林

在高考复习中要注意知识间的联系与结合.数列是高考的重点与难点，概率问题也在近几年的高考中份量越来越大.笔者在此选择了三道数列与概率结合的典型例题，献给读者朋友，不足之处，请不吝赐教.

例1（2006年北京春季高考题）A、B两人拿两颗骰子做抛掷游戏，规则如下：若掷出的点数之和是3的倍数，则由原掷骰子的人继续掷，若掷出的点数和不是3的倍数，就由对方接着掷.第一次由A开始掷，设第n次由A掷的概率为Pn，求Pn的表达式（用n表示）.

解：由题意可知，第n次由A掷有两种情况：①第n-1次由A掷，且此时抛出骰子的点数和为3的倍数，此时概率为P=；②第n-1次由B掷，且此时抛出骰子的点数和不是3的倍数，此时概率为（1-Pn-1）.由这两种情况是互斥的，得（1-Pn-1），（n≥2，n∈N）.将上式变形为：

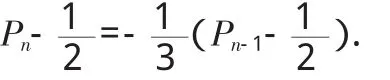
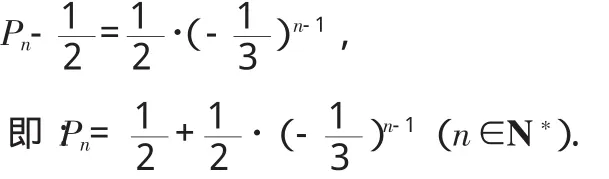
例2 某人玩“掷硬币走跳棋”的游戏，已知硬币出现正反面的概率都是0.5，棋盘上标有第0站、第1站、…、第100站，一枚棋子开始在第0站，棋手掷一次硬币棋子向前跳动一次，若掷出正面，棋子向前跳1站（即从第k站跳到第k+1站），若掷出反面（即从第k站跳到第k+2站），棋子向前跳两站；直到棋子跳到第99站（胜利大本营）或跳到第100站（失败大本营）时，游戏结束.设棋子跳到第n站的概率为Pn.

（1）求 P0，P1，P2；

（3）求Pn.

解：（1）棋子开始在第0站为必然事件，故P0=1.第一次掷硬币出现正面，棋子跳到第1站，其概率为，因此棋子跳到第2站应从如下方面考虑：

（2）棋子跳到第 n（2≤n≤99）站有且只有以下两种情况：

（3）由（1）、（2）知数列{Pn-Pn-1}是首项为，公比为的等比数列，由等比数列的通项公式知：

Pn-Pn-1=

由迭加法得：

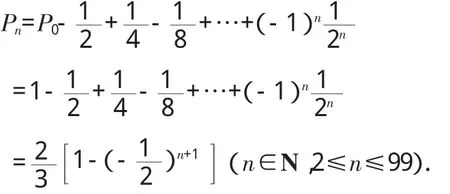
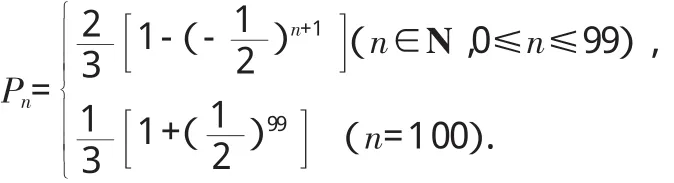
例3 质点A位于数轴x=0处，质点B位于x=2处.这两个质点每隔1秒都向左或向右移动1个单位，设向左移动的概率为，向右移动的概率为

（1）求3秒后，质点A在点x=1处的概率；

（2）求2秒后，质点A、B质点在点x=2处的概率；

（3）假若质点C在x=0，x=1两处之间移动，并满足：当质点C在x=0处时，1秒后必移到x=1处；当质点C在x=1处时，1秒后分别以的概率停留在x=1处或移动到x=0处，今质点C在x=1处，求8秒后质点C还在x=1处的概率；

解：（1）3秒后，质点 A到 x=1处，必须经过两次向右，一次向左移动.

（2）2秒后，质点A、B同时在点x=2处，必须质点A两次向右，且质点B一次向左，一次向右，

（3）设第n秒后，质点C在x=1处的概率为xn，质点C在x=0处的概率为yn，由题意可知

由xn+yn=1得

∴ {3xn-2}是首项为，公比为的等比数列.

小结：概率问题在高考中常常以单元内的知识的横向综合为主要题型，与单元外知识的纵向综合屈指可数，但随着近几年高考对概率问题考察程度的进一步加深，难度的加大，复习时应引起足够的重视。本文3道例题，不仅融合自然，而且还突出了能力立意这个核心。