一种新的卫星导航宽带干扰抑制方法

白 燕，卢晓春，王 瑾，韩 涛

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；

一种新的卫星导航宽带干扰抑制方法

白 燕1，2，3，卢晓春1，2，王 瑾1，2，3，韩 涛1，2，3

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；

3.中国科学院大学，北京 100039)

宽带干扰是卫星导航系统中常见的一种压制性干扰，也是危害较大的一种干扰方式。针对线性调频宽带干扰，以离散傅里叶变换为信号分析工具，并在此基础上提出一种基于NEW-MDCFT的宽带干扰抑制算法。详细介绍了该算法的模型和实现方式，并针对叠加了线性调频宽带干扰信号的北斗系统B1信号，采用该算法进行计算机仿真，给出干扰抑制前后信号的时域性能、频域性能、捕获性能以及跟踪性能等特性。结果表明，基于NEW-MDCFT的抑制算法具有良好的线性调频宽带干扰抑制性能，可以使接收机在干扰环境下顺利完成捕获和跟踪，大大增强了卫星导航信号的抗干扰能力。

卫星导航；线性调频宽带干扰；干扰抑制

1 引言

卫星导航定位技术在现代军事、民用领域中发挥越来越重要的作用，但由于卫星导航信号自身信号较弱，容易受到各种干扰的影响，从而对接收信号的性能造成损失[1-2]。实际空间环境中的干扰可分为人为干扰和非人为干扰两类。不同干扰类型有不同的特性，不同的特性对应不同的干扰抑制方法。非人为干扰大多为来自自然界的干扰，如系统内部的干扰、噪声干扰、多径干扰等，这些干扰是客观存在，非敌意的。目前对于非人为干扰只能进行削弱，而不能完全消除。对于人为干扰，是一种故意干扰，意在对敌方的通信实施干扰，达到破坏对方通信的目的，人为干扰可以利用信号处理的方法对其进行消除或削弱。

一般来说，对卫星导航系统接收机威胁最大的人为干扰可能是压制式干扰[3-4]。压制式干扰采用一部干扰机来扰乱该地域出现的所有卫星信号，这种干扰方式又可分为宽带和窄带干扰。宽带干扰采用一般的时域或频域的抑制技术，很难达到理想的抑制效果，而必须考虑采用一些其他的滤波方法[5-7]。本文主要讨论卫星导航、电子对抗等环境中常用的一种干扰样式即线性调频(line frequency modulation，LFM)干扰。LFM信号作为一种大时间-带宽积的非平稳信号[8-9]，其频谱在整个带宽内比较平坦，而在带外的衰减很快，能量在带宽内非常集中。当干扰为LFM信号且干扰带宽与导航信号的带宽相同或相差不多时，卫星导航扩频系统的性能会急剧下降，采用通常的自适应滤波算法此时很难达到有效干扰抑制效果。针对这种情况，本文提出了一种基于NEW-MDCFT的抑制方法，该方法以离散傅里叶变换为基础，可以有效地对LFM宽带干扰进行抑制。

2 离散傅里叶变换基础

离散Chirp-Fourier变换[10-12](discrete Chirp-Fourier transform，DCFT)是一种有效的线性调频信号检测技术，它是离散Fourier 变换(discrete Fourier transform，DFT)的推广，特别适合于LFM信号。

假设x(n)(0≤n≤N-1)为N点的离散LFM信号，定义DCFT为[13]

(1)

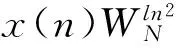
(2)

文献[13]证明，若采样点N为质数且k0、l0为整数(0≤k0,l0≤N-1)，x(n)的DCFT幅值为

(3)

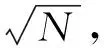
(4)

考虑式(5)形式的模拟Chirp信号

xa(t)=exp(j2π(α0t+β0t2))

(5)

设总采样点数为N(N为质数)，采样时刻满足t=nT/N1/3，n=0,1,2,…,N-1， 则总采样时间为N2/3T， 采样后的离散线性调频类(Chirp-like)信号可以变为

(6)

式(6)中，k0=a0TN2/3，k0=β0TN1/3。DCFT匹配LFM信号需要满足两个约束条件：1)信号长度必须为质数；2)离散LFM信号的参数k0、l0必须是整数或极为接近整数。

两个约束条件中条件1比较容易满足，但条件2的要求极为苛刻。因为在给定质数采样点N的情况下，N1/3和N2/3必定不是整数，它们分别与参数a0T和β0T相乘几乎不可能是整数。更为严重的是，即使k0和l0偏离整数一个不大的数据，定义的DCFT对Chirp信号的检测性能将急剧下降。

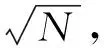
为了克服DCFT的缺点，对DCFT的定义进行了修正，它对信号的采样点数和信号参数不附带任何约束条件，适应对离散LFM信号进行检测和参数估计，即提出修正离散Chirp-Fourier变换(modifiedDCFT，MDCFT)[14]。

定义MDCFT公式为

(7)

MDCFT反变换(inverseMDCFT，IMDCFT)公式为

(8)

对模拟LFM进行N点采样(N可以为任意整数)，采样时刻为

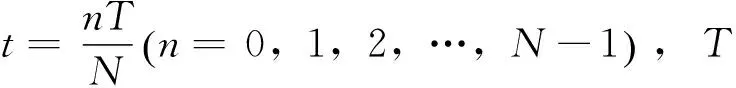
采样后的离散LFM信号为

(9)

式(9)，中k0=α0T,l0=β0T2， 这里k0、l0不一定为整数。

MDCFT与DCFT相比，有如下几点特点：

1)MDCFT对信号的总采样点数和信号参数没有任何约束条件，它对信号参数的精确估计范围也远大于DCFT，所以更有意义。

2)MDCFT对LFM信号的能量聚集性与DCFT相比略有降低。

3)DCFT和MDCFT均为线性变换，在存在多个LFM信号分量时不存在交叉项，这是它们的主要优点。

在理想情况下，当采样时钟没有偏差时，k0、l0都是整数或接近整数，MDCFT能够匹配k0和l0为整数的情况，干扰抑制算法能够很好的抑制LFM干扰；但当接收端采样时钟不准确时，LFM干扰的k0和l0有分数部分，这时会出现以下问题：

1)MDCFT会出现能量泄露，从而不能准确检测实际幅度的最大值。

2)得到的干扰信号的参数估计值出现较大偏差，从而影响干扰抑制的性能。

针对出现的问题1及问题2，为了匹配k0和l0的小数部分，本文采用一种新颖的MDCFT变换算法，即NEW-MDCFT变换

(10)

式(10)中，δk,δl∈[-0.5,0.5]。该定义能有效地匹配由采样时钟偏差所引起的问题，更好地匹配LFM干扰信号。

对于如下形式的离散Chirp信号

(11)

当k0、l0为整数且0≤k0,l0≤N-1，x(n)的NEW-MDCFT幅值为

(12)

当k0、l0含有小数部分时，分别改变δk、δl可有效地补偿小数部分，此时NEW-MDCFT的幅值与式(11)相同。

3 基于NEW-MDCFT的干扰抑制方法

3.1 干扰抑制模型

基于NEW-MDCFT的干扰抑制模型原理如图1所示。基本思想是对接收信号r(n)进行NEW-MDCFT变换，形成(k,l)二维平面，在此平面上进行二维搜索得到的坐标位置即为(k,l)的估计值。由于NEW-MDCFT变换保留了干扰的幅度和相位特性，因此可将峰值点的幅度经过变换作为干扰信号幅度的估计值，峰值点的相位直接作为相位的估计值。根据得到的估计参数重构干扰j(n)， 然后从接收信号中减去重构后的干扰信号得到干扰抑制后的信号y(n)。

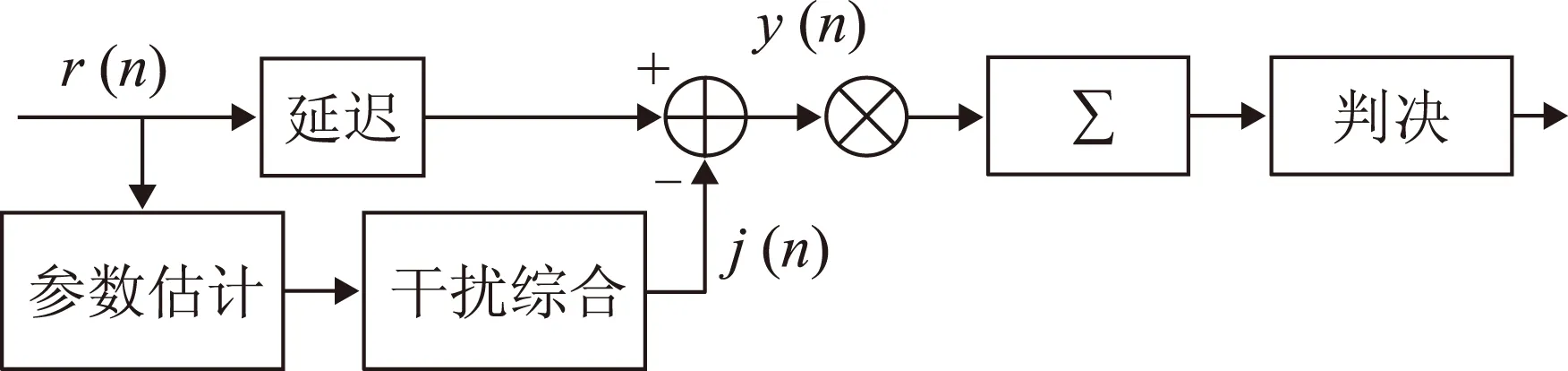
图1 基于NEW-MDCFT的抑制模型

3.2 干扰抑制的实现步骤

1)粗略估计干扰的参数

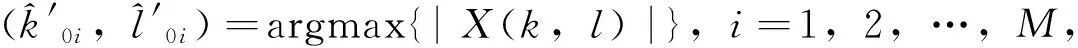
2)精确估计干扰的参数(a0i,φ0i,k0i,l0i),i=1,2,…,M。

(12)

3)根据步骤2)中所得到的估计的各个干扰成分的参数重构干扰，得到干扰j(n)的估计为

(13)

4)从接收信号r(n)中减去综合重构的干扰信号j(n)， 即得到干扰抑制后的信号y(n)， 然后就可以对y(n)进行解扩和判决等其他处理。

4 干扰抑制性能仿真

为了验证上述干扰抑制算法对LFM干扰的抑制性能，利用国家授时中心的全球卫星导航系统(globalnavigationsatellitesystem，GNSS)信号质量监测采集系统采集到一组我国北斗卫星导航系统简称北斗系统(BeiDounavigationsatellitesystem，BDS)B1信号，并叠加一定能量的线性调频干扰信号，干扰的带宽覆盖整个导航信号的带宽。采用基于NEW-MDCFT的抑制算法对混有干扰的实测导航信号进行干扰抑制，给出干扰抑制前后的信号时域性能、频域性能图、捕获性能、以及跟踪性能，分析该干扰抑制算法的性能。

4.1 时域性能仿真结果

当对BDS B1信号混叠进入干信比为-10 dB的线性调频干扰后，信号的时域图如图2所示，可以看出，BDS卫星导航信号叠加了线性调频干扰后，其波形存在明显的干扰杂波，而经过基于NEW-MDCFT的干扰抑制后如图3，信号波形变得较为纯净。

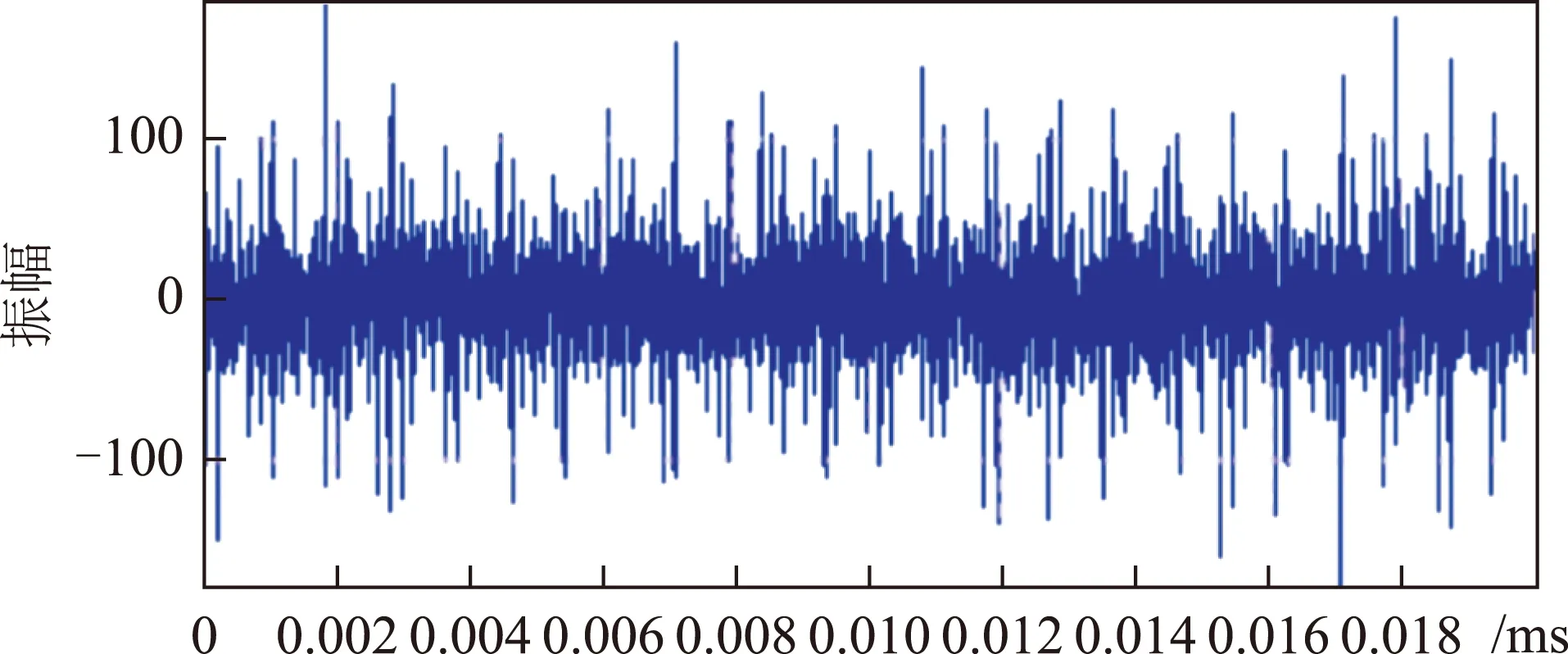
图2 干扰抑制前时域性能图

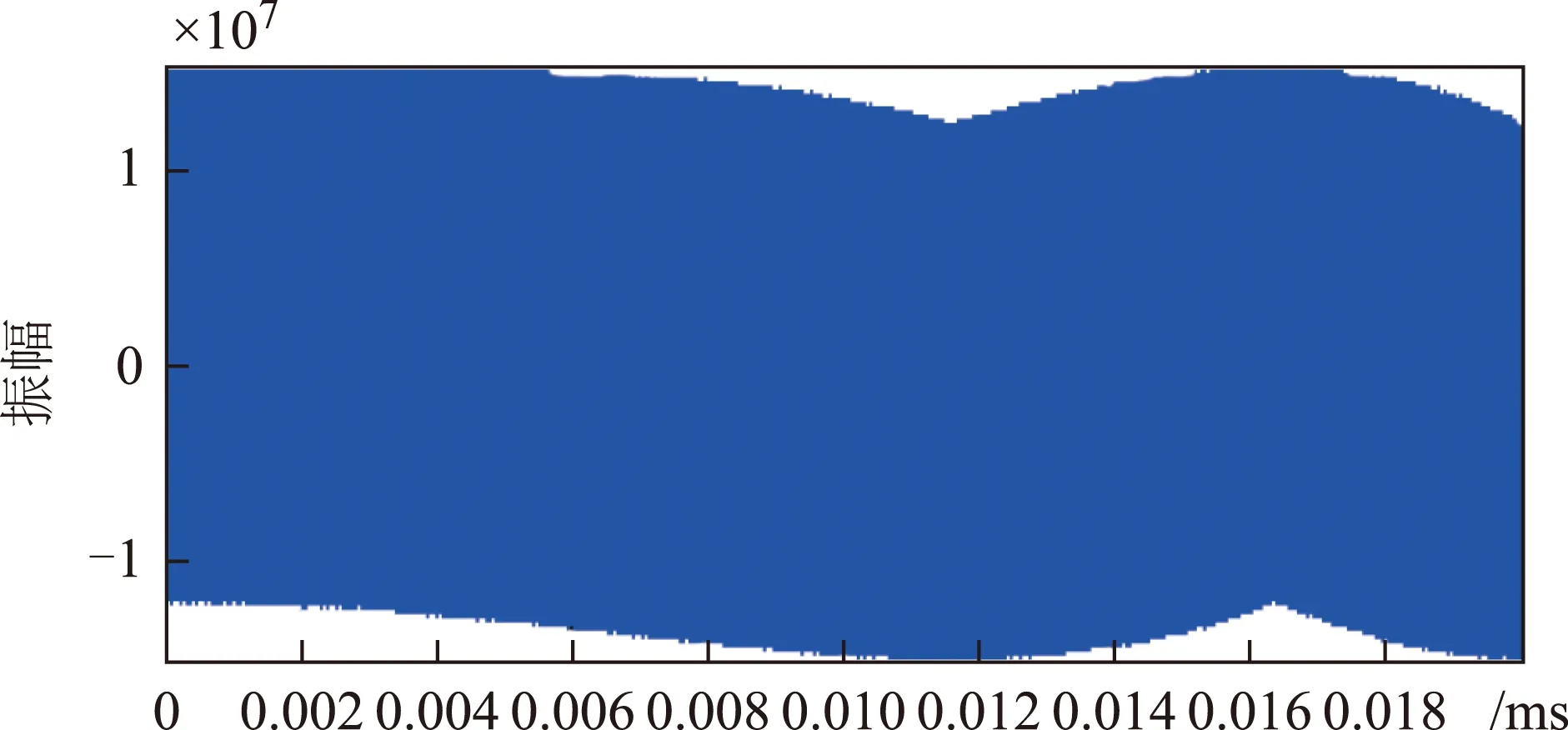
图3 干扰抑制后时域性能

4.2 频域性能仿真结果

从图4可以看出，当叠加了LFM干扰后，干扰的能量已经完全覆盖了卫星导航信号，而经过干扰抑制后，如图5，可以明显看出北斗卫星导航信号的频谱，其中心频点在37.5 kHz的中频上，在有用信号带宽外，存在部分其他的谐杂波分量。

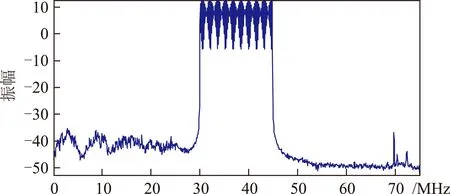
图4 干扰抑制前频域性能图

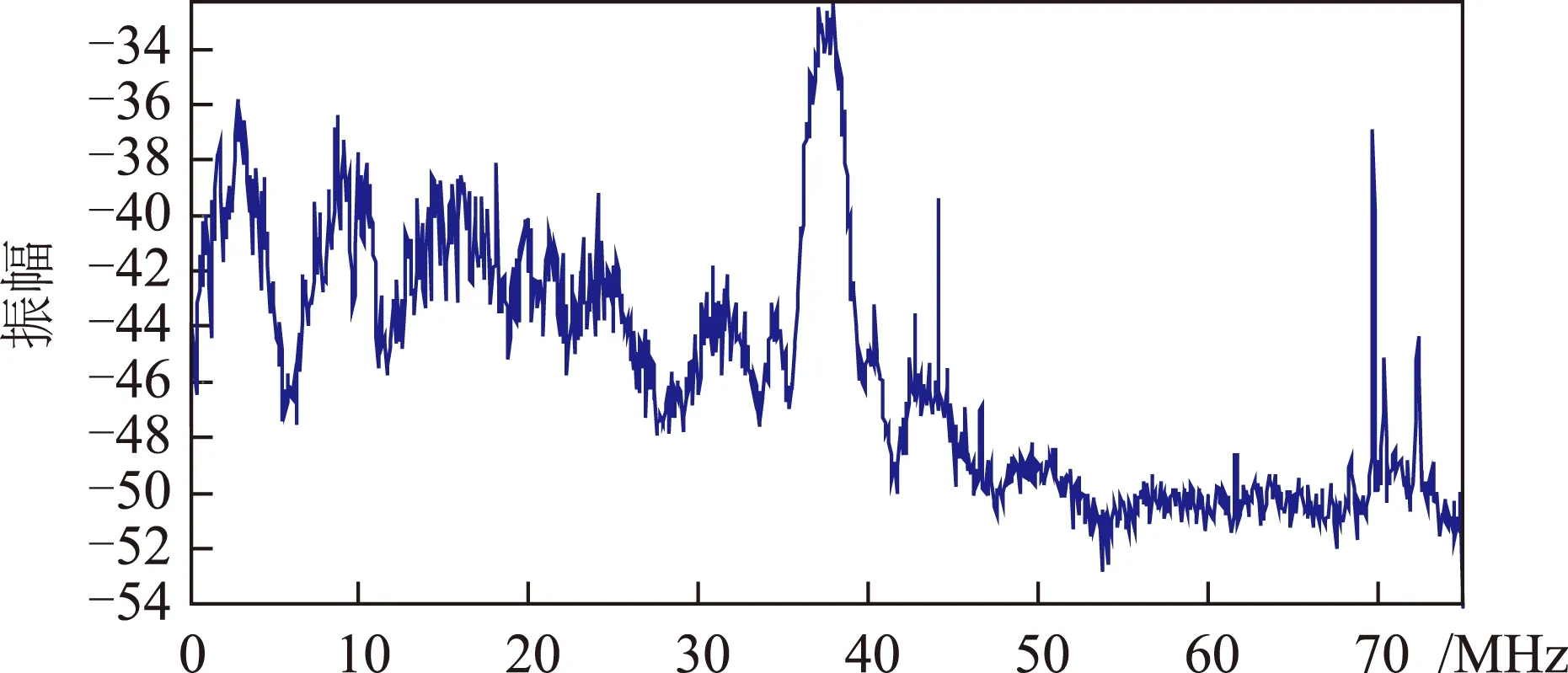
图5 干扰抑制后频域性能图

4.3 捕获性能仿真结果

当将-10 dB干信比的线性调频扰叠加在卫星导航信号上，此时信号能量被干扰所覆盖，导致接收机无法识别卫星，从而无法实现导航信号的捕获跟踪。

而通过基于NEW-MDCFT算法的干扰抑制后，信号可以顺利完成捕获和跟踪，如图6所示。

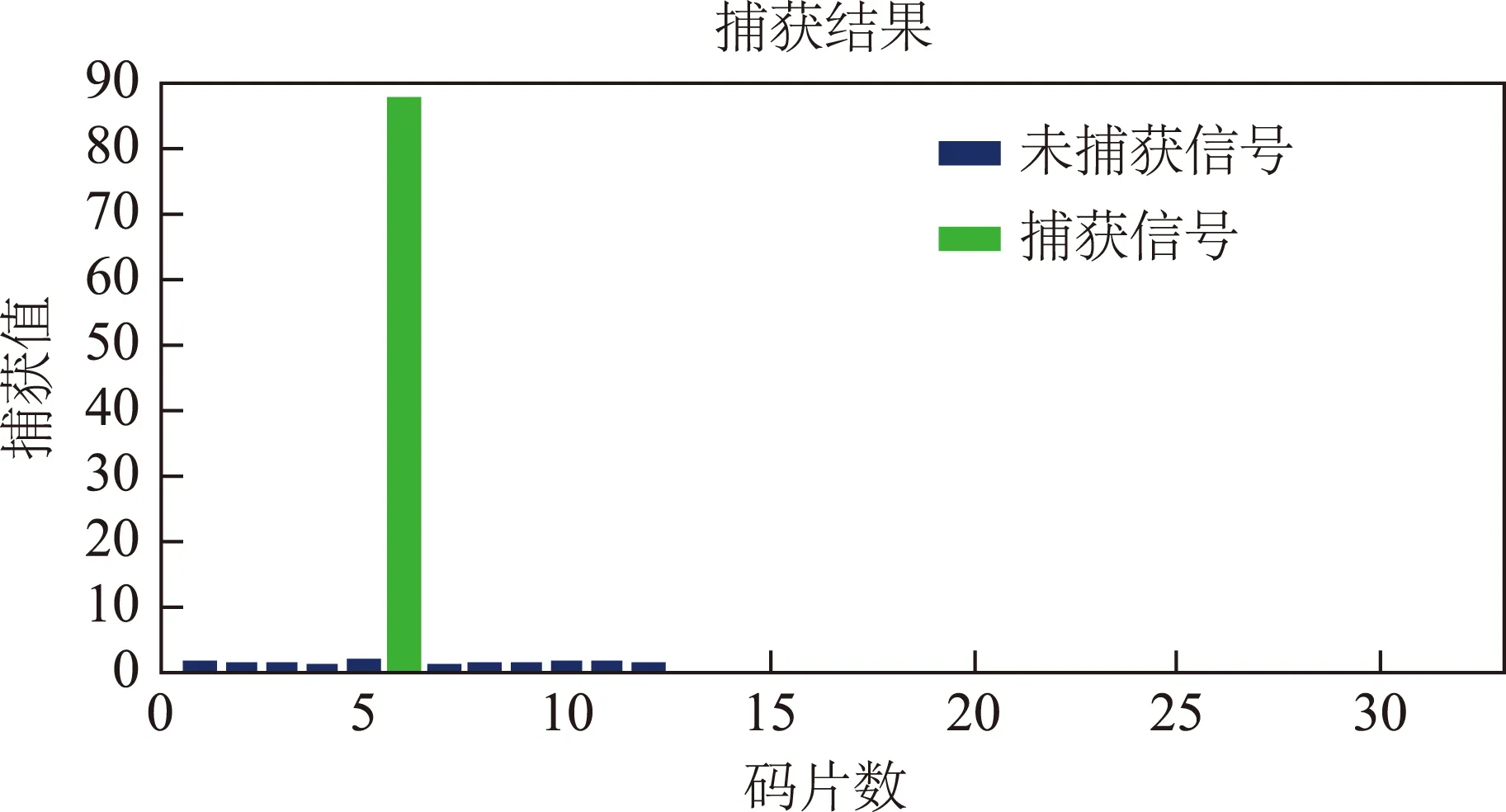
图6 干扰抑制后捕获性能图

4.4 跟踪性能仿真结果

如图7所示，经过基于NEW-MDCFT算法的干扰抑制后，顺利完成跟踪。

图7 干扰抑制后跟踪性能图

4.5 仿真分析

从上述仿真结果可以看出，当没有采用干扰抑制算法时，卫星导航信号的时域图和频谱图明显的受到严重线性调频干扰的影响，并且无法识别卫星，无法完成导航信号的捕获和跟踪。而经过干扰抑制算法之后，信号受到的LFM干扰基本被滤除，且顺利地完成了信号的捕获和跟踪程序。因此，基于NEW-MDCFT的干扰抑制算法可以较好的对线性调频干扰进行抑制。

5 结束语

研究卫星导航系统接收机抗干扰技术，对于提高卫星导航系统在复杂电磁环境下的工作性能、增强其在各种环境中的适用性具有重要意义。本文以卫星导航系统中常见的宽带线形调频干扰为研究对象，以离散Chirp-Fourier变换为信号分析工具，并在此基础上提出基于NEW-MDCFT的干扰抑制算法。通过对北斗导航卫星信号叠加线性调频宽带干扰后的混合信号进行计算机仿真，比较该干扰抑制算法在干扰抑制前后对导航信号的时域、频域、捕获、跟踪性能等的影响。结果表明，该干扰抑制算法具有较好的干扰抑制性能。

[1] MAY M M，LAINEZ M D，MARTIN J R，et al.GNSS，an Evolving Technology.Current Systems Evolutions and Future Perspectives[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011).Portland，OR：The Institute of Navigation，2011：3083-3101.

[2] 刘基余.GNSS 全球导航卫星系统的发展与挑战[EB/OL].[2014-05-23].http：//www.docin.com/p-117236353.html.

[3] KAPLAN E D，HEGARTY C J.GPS原理与应用[M].寇艳红，译.2 版.北京：电子工业出版社，2007.

[4] 费华连.导航战中的GPS干扰与抗干扰技术[J].航空电子技术，2001，32(1)：19-22.

[5] 朱春华，穆晓敏.DSSS系统中线性调频干扰抑制技术研究[J].电波科学学报，2003，18(3)：341-351.

[6] 刘艳良，孔军辉.直接序列扩频通信系统LFM干扰抑制技术研究[J].电子信息对抗技术，2013，7(4)：56-60.

[7] LIU Yao，NING Peng，DAI Huai-yu，et al.Randomized Differential DSSS：Jamming-Resistant Wireless Broadeast Communication[C]//Proceedings of the 29th IEEE International Conference on Computer Communications (IEEE INFOCOM 2010).San Diego，CA：IEEE，2010：1-9.

[8] 朱健东，赵拥军，唐江.线性调频连续波信号的周期分数阶Fourier变换检测与估计[J].电子与信息学报，2013，35(8)：1827-1833.

[9] 张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业出版社，1998.

[10]WEI Yong-mei，BI Guo-an.Broadband Interference Suppression In DS-SS System with Modified Chirp Fourier Transform[C]//Proceedings of the 9th IEEE International Conference on Communications Systems(ICCS 2004).Singapore：IEEE，2004：640-644.

[11]FAN Bo，ZHANG Kai，QIN Yu-liang，et al.Discrete Chirp-Fourier Transform-based Acquisition Algorithm for Weak Global Positioning System L5 Signals in High Dynamic Environments[J].Radar，Sonar & Navigation，IET，2013，7(7)：736-746.

[12]WU Liang，WEI Xi-zhang，YANG De-gui，et al.ISAR Imaging of Targets with Complex Motion Based on Discrete Chirp Fourier Transform for Cubic Chirps[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50(10)：4201-4212.

[13]XIA Xiang-gen.Discrete Chirp-Fourier Transform and Its Application to Chirp Rate Estimation[J].IEEE Transactions on Signal Processing，2000，48(11)：3122-3133.

[14]孙泓波，郭欣，顾红，等.修正离散Chirp Fourier变换在运动目标检测中的应用[J].电子学报，2003，31(1)：1-4.

An Interference Suppression Method Based on NEW-MDCFT in Satellite Navigation System

BAI Yan1，2，3，LU Xiao-chun1，2，WANG Jin1，2，3，HAN Tao1，2，3

(1.National Time Service Center，Chinese Academy of Sciences，Xi’an 710600，China；2.Key Laboratory for Precise Navigation and Timing Technology，National Time Service Center，Chinese Academy of Sciences，Xi’an 710600，China；3.Universisty of Chinese Academy of Sciences，Beijing 100039，China)

Wideband interference is common oppressive which impact on the receiver performance badly in the satellite navigation system.In this paper，aiming at the linear frequency modulation (LFM) wideband interference，an interference suppression method based on NEW-MDCFT is presented，and the model and implementation method of the suppression algorithm have been introduced.By adding the LFM jamming to the COMPASS B1 signal，the interference suppression method is simulated，and time domain performance，frequency domain performance，acquisition performance and tracking performance of the signal before and after interference suppression have been given.The results indicate that，the suppression method based on NEW-MDCFT has good LFM interference suppression performance and is able to perform good interference suppression for seriously-interfered information navigation signal，so that the receiver can accomplish acquisition and tracking smoothly.

wideband interference；LFM；interference synthesis

2014-04-29

国家自然科学基金(11203027)。

白燕(1975)，女，陕西清涧县人，副研究员，博士，主要从事卫星导航技术及信号处理等方面的研究工作。

TN967

A

2095-4999(2015)-01-0061-05