基于循环谱和稀疏表示的多信号调制识别
2015-05-05王兰勋孟祥雅佟婧丽
王兰勋,孟祥雅,佟婧丽
(河北大学 电子信息工程学院,河北 保定 071002)
基于循环谱和稀疏表示的多信号调制识别
王兰勋,孟祥雅,佟婧丽
(河北大学 电子信息工程学院,河北 保定 071002)
针对难以识别时频重叠的多信号问题,提出一种不用分离混合信号即可识别信号类型的新方法。该方法针对各种调制循环谱的不同,用稀疏表示提取各信号的特征,最后根据提取的特征利用支持向量机对信号进行识别分类。经理论推导和仿真实验得出:该方法对噪声具有一定的鲁棒性,在较低信噪比条件下仍能保持较好的识别性能,在信噪比为-4 dB时,对单信号和混合信号的正确识别率分别可达到93.5%和90.67%。
循环谱;稀疏表示;支持向量机;调制识别
随着信息时代的飞速发展,调制信号识别技术也有了很大的提高,在当今的无线通信领域占有举足轻重的地位,在频谱管理、信号认证、通信监视、干扰识别和电子对抗等多个领域[1]有着广泛的应用,因此得到国内外学者的重视并对其进行了深入研究。在自动调制识别技术的发展过程中提出了两种分类算法,分别是基于似然方法和基于特征方法。由于基于似然方法识别范围比较小,计算难度比较大,通常性能较为优越。而操作比较简单的基于特征方法,是由两部分组成,分别是特征提取和分类识别,而特征提取的实质是对源信号从原始的观测空间到易于分类的特征空间的映射。
MFSK和MPSK信号作为常用的数字通信信号,许多文献对其发展都有论述[2]。文献[3]采用信号的平方谱和4次方谱的强度与位置作为特征参数,对单信号进行调制类型识别,文献[4]采用高阶累积量和分形盒维数两个联合参数对单个调制信号进行识别,文献[5]利用循环累积量的特征对多个调制信号进行识别并对信号个数进行了估计,文献[6]根据每个信号循环谱有不同循环频率的特征对多信号进行调制类型识别,文献[7]把信号频谱和稀疏表示相结合对单个信号进行调制类型识别。
针对调制信号循环谱的特点,本文提出了一种新的调制方式识别的方法。该方法把稀疏表示与循环谱相结合,把单信号和多信号的稀疏系数作为特征参数 ,最后根据稀疏系数利用支持向量机对调制信号进行分类。本文最后对只利用循环谱的方法[6]、频谱与循环谱结合的方法[7]和利用循环谱与稀疏表示相结合的方法进行了比较,实验结果表明:本文提出的方法对噪声具有更好的鲁棒性,并证明了该方法的有效可行性。
1 信号循环谱
若信号x(t)为广义循环平稳信号,则其循环自相关函数为
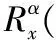
(1)
经过傅里叶变换得到循环谱为
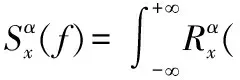
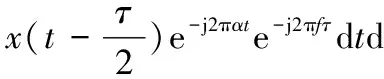
(2)
式中:T表示所取得信号的时间长度;f表示频率;α表示循环频率。
调制信号的相关函数在时间变化的同时具有周期性,从而反映出它在一定条件下具有平稳特性,因此调制信号也被称为循环平稳信号。调制信号的循环平稳特征可以用循环谱来体现,循环谱既包含信号的频率域信息也包含循环频率域信息,因此它可以更全面地反映每类调制信号的特性。高斯噪声或非高斯噪声不是周期平稳的信号,它的周期统计量值为零,而且噪声只对在循环频率为零的循环谱有影响,所以调制信号循环谱对噪声有一定的鲁棒性。
若存在多个调制信号,且各信号间保证相互独立,则多个信号的循环谱可以用各个信号循环谱的和来表示[6],例如,当存在两个线性混合的信号时,混合信号的循环谱可表示为
(3)
本文中采用如下步骤进行循环谱估计:
1)给信号加以T为窗宽的矩形窗,并进行傅里叶变换,即
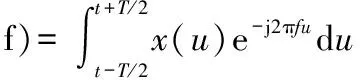
(4)
2)根据公式计算信号的循环谱密度函数为
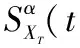
(5)
3)对循环谱密度函数进行估计为
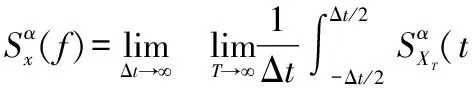
(6)
式中:Δt表示接收数据长度。
2 稀疏表示
稀疏表示在压缩采样、信号去噪、人脸识别、参数估计等领域有着广泛的应用,在广义上,稀疏表示的数学模型[7]可以表示为
y=Ds+z
(7)

为了能够得到最优稀疏系数,应满足条件

(8)
式中:‖s‖0表示l0范数,即s中含有非零值的个数;ε为设定的错误容限。
要想得到唯一的最优稀疏解,冗余字典D和s的稀疏度就要满足RIP条件,这又是一个NP问题,求解困难,所以当稀疏系数能够达到足够稀疏时,由于l0范数最优解等价于l1范数的最优解,采用l1范数来求解最优稀疏解[7],即
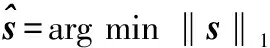
(9)
稀疏表示的过程(即字典的学习和稀疏编码实现的过程)既包括l1范数的约束,还包含对重构误差和稀疏度的最小化,因此使用稀疏表示不仅能增强特征自身的稀疏性,还能消除一定的噪声干扰,从而使根据稀疏表示得到的稀疏系数具有更好的判别性,更利于分类识别的进行。
3 循环谱与稀疏表示相结合的方法
通过以往的分析可知,光滑信号在它的频域内是稀疏的[8],而调制信号的自相关函数在时域内仍是光滑的,所以调制信号的循环谱具有一定的稀疏性,由此提出,用循环谱与稀疏表示相结合的方法对调制信号进行识别分类。
循环谱与稀疏表示相结合的分类算法步骤如下:
1)取足够多的调制信号循环谱,由于循环谱具有较高的维度,若直接用它训练字典会使计算量过大,所以要用PCA的方法[9]对循环谱数据的维度进行降维,变换后的前100维数据累计贡献率已达到94.6%,因此取每个信号循环谱变换后的前100维数据作为训练样本,构建训练集。
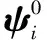
3)根据K-SVD算法[7]和OMP[10]算法,训练出最优过完备字典D(使任何一个测试样本能由D中相同调制类型的原子线性表示)。
4)每类信号有不同的稀疏系数,因此把稀疏系数作为分类特征。利用OMP算法对所取训练样本求解稀疏系数,并由得到的稀疏系数构建训练集train-SR。
5)把训练集train-SR中的数据作为支持向量机的训练样本,建立用于对调制信号进行分类的支持向量机模型。
6)用OMP法求解测试集中各测试样本相对于过完备字典D的最优稀疏系数,利用支持向量机对各测试样本所对应的稀疏系数进行分类,即对各类调制信号分类。
4 实验仿真
本文采用MATLAB对上述方法的有效性进行仿真验证,本文中采用的数字调制信号的采样频率为4 kHz,载波频率为1 kHz,码元速率为500 bit/s,码元个数为1 000个。
本文介绍了4种调制信号,分别是BPSK,QPSK,2FSK,4FSK。混合识别字典包含单信号和混合信号,由10种类型的原子构成,分别是BPSK,QPSK,2FSK,4FSK,BPSK和QPSK,BPSK和2FSK,BPSK和4FSK,QPSK和2FSK,QPSK和4FSK,2FSK和4FSK。字典共包含1 200个原子,其中每类信号包含120个原子,K-SVD算法的迭代次数为300次,支持向量机采用的核函数是径向基函数。
把高斯白噪声加入到调制信号中去,以2 dB为间隔在信噪比为-6~+20 dB的条件下,每类信号分别取500个降维后的循环谱数据,其中200个作为训练样本,300个作为测试样本。由于不同的混合信号的功率比会影响信号识别的准确度,本文考虑分别构建混合信号功率比为1∶1和2∶1的混合识别字典。
由图1可知,对于单信号的调制识别,本文方法能够在较低信噪比的条件下达到较高的识别率。由图2可以看出,当存在两个不同调制方式的混合信号时,在较低信噪比的条件下通过本文方法仍可以对混合信号的调制类型进行较好的识别。由图3可知,在低信噪比条件下,当混合信号的功率差变大时,信号的识别率会降低,这是由于当两信号中一个功率较大时,另一个信号的特征可能被掩盖或忽略成噪声,使实际的信噪比降低,造成识别率比图2有所降低。

图1 4类单个信号的正确识别率

图2 在功率比为1∶1的条件下混合信号的正确识别率

图3 在功率比为2∶1的条件下混合信号的正确识别率
图4和图5分别对单个信号和混合信号的不同识别方法进行了比较。从图中可以看出,在信噪比为 -4 dB时,对单信号和多信号的识别率分别可达到93.5%和90.67%,而频谱与稀疏表示相结合的方法对单信号和多信号的识别率分别可达到83%和76%,只用循环谱的方法对单信号和多信号的识别率只能分别达到75%和68%,从而得出本文方法具有更好的识别效果。由理论分析可知循环谱有一定的抗噪声性能,稀疏表示不仅有一定的去噪效果,还能增强信号能量的集中度,而频谱的抗噪声性能比循环谱差,信号频谱与稀疏表示相结合的方法和循环谱的方法都只具有单重抗噪性能,而本文方法具有双重抗噪性能,所以在较低信噪比的条件下,本文方法对于调制信号的识别具有一定的优越性。
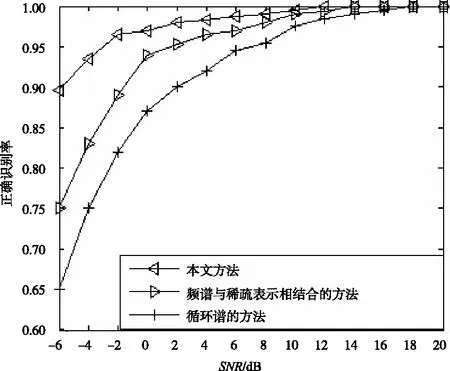
图4 不同的方法对单信号正确识别率的影响
5 小结
本文针对单个调制信号和时频重叠的混合调制信号的识别问题,提出了将信号循环谱与稀疏表示相结合的新识别方法。该方法首先求出调制信号的循环谱,然后把每类信号循环谱进行稀疏表示,并求解稀疏系数,把稀疏系数作为识别特征,最后根据稀疏系数利用支持向量机对调制信号进行分类。经仿真验证,在低信噪比的条件下,本文方法具有良好的识别性能。
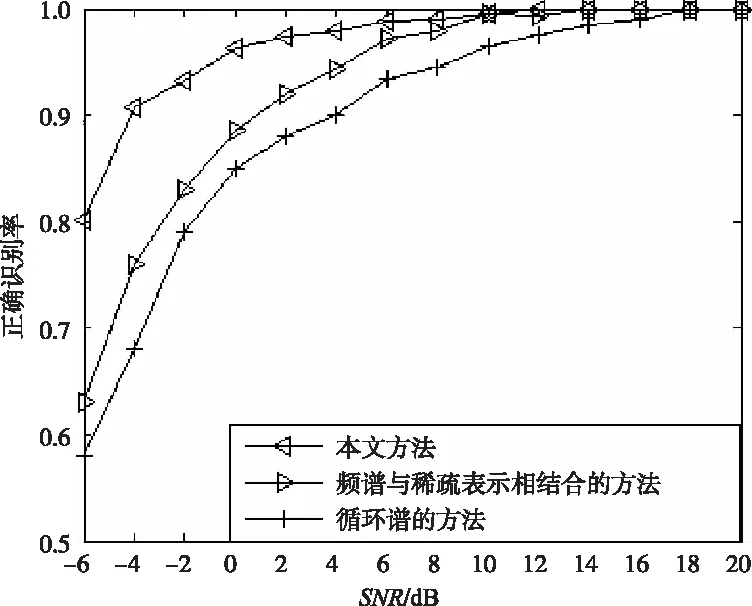
图5 在混合信号功率比为1∶1的条件下不同方法对正确识别率的影响
[1]靳晓艳,周希元.一种最大似然调制识别的快速算法[J].系统工程与电子技术,2013,35(3):615-618.
[2]DOBRE O A, BD A,BAR-NESSY,et al. Survey of autom aticmodulation classification techniques classical approaches and new trends[J].IET Commum., 2007,1(20):137-156.
[3]邓璋,徐以涛,王乃超.基于信号谱线特征的调制方式识别[J].通信技术,2013,46(1):7-9.
[4]党月芳,徐启建,张杰,等.高阶累积量和分形理论在信号调制识别中的应用研究[J].信号处理,2013,29(6):761-765.[5]赵宇峰,曹玉建,纪勇,等.基于循环频率特征的单信道混合通信信号的调制识别[J].电子与信息学报,2014,36(5):1203-1208.
[6]余志斌,丁宁宇.基于循环谱包络的多信号调制识别[J].计算机应用,2012,32(8):2119-2122.
[7]王振宇,秦立龙,刁俊良.基于K-SVD和稀疏表示的数字调制模式识别[J].计算机科学,2013,40(10):65-67.
[8]CHEN Yun, LIU Jian, LV Shoutao. Modulation classification based on bispectrum and sparse representation in cognitive radio[C]//Proc. IEEE International Conference on Communication Technology. [S.l.]:IEEE Press,2011:250-253.
[9]ZHOU G, YANG Z, WU Z, et al. Non-orthogonal joint diagonalization with diagonal constraints[J].Progress in Natural Science,2008,18(6):735-739.
[10]陈佳,张永平.图像过完备稀疏表示理论及应用综述[J].电视技术,2012,36(17):40-43.
王兰勋(1956— ),教授,主要从事数字通信与信息编码方面研究;
孟祥雅(1990— ),女,硕士生,主研调制识别;
佟婧丽(1989— ),女,硕士生,主研信道编码盲识别。
责任编辑:薛 京
Multi-signals Modulation Recognition Based on Cyclic Spectrum and Sparse Representation
WANG Lanxun, MENG Xiangya, TONG Jingli
(CollegeofElectronicandInformationalEngineering,HebeiUniversity,HebeiBaoding071002,China)
For the modulation recognition problem of several time-frequency overlapping modulation signals, a new method that can identify the signals mixed signal types without separation is proposed. For different cyclic spectrum of different modulation signals, the features can be extracted by using sparse representation, and finally according to the extracted feature, support vector machine is used to recognition and classification. Theoretical analysis and experimental simulations obtain that this method has a certain robustness of noise, it still has a good recognition performance at low SNR. When the SNR is -4 dB, the correct recognition rate of single and mixed signals can respectively reach 93.5% and 90.67%.
cyclic spectrum; sparse representation; SVM; modulation recognition
河北省自然科学基金项目(F2014201168)
TN911.72
A
10.16280/j.videoe.2015.01.023
2014-06-10
【本文献信息】王兰勋,孟祥雅,佟婧丽.基于循环谱和稀疏表示的多信号调制识别[J].电视技术,2015,39(1).
