基于三相Z源并网逆变器的间接单周控制策略

邓 强，杨燕翔，田 果，易忠尧，赵 帆

(西华大学电气信息学院，四川成都 610039)

基于三相Z源并网逆变器的间接单周控制策略

邓 强，杨燕翔，田 果，易忠尧，赵 帆

(西华大学电气信息学院，四川成都 610039)

提出一种基于三相Z源网络的间接单周控制方式，解决常规控制方式所带来的系统复杂与响应速度慢的缺点。结合Z源阻抗网络中输入输出关系，建立三相Z源并网逆变器状态平均方程数学模型，运用单周控制原理推导控制方程，以实现单位功率因数并网。仿真结果表明，基于单周控制的三相Z源并网逆变器能在单个工频周期内(0.02s)实现单位功率因数并网，其输出电流谐波畸变率小于1%，且输出几乎不受输入电压波动的影响。与传统Z源并网逆变器比较，基于单周控制的间接电流控制方式能在没有电流采样环节的情况下快速实现单位功率因数并网，具有动态响应快、稳定性较强、鲁棒性较优的特点。

三相Z源并网；单周控制；状态平均方程；单位功率因数

0 引 言

近年来，世界范围内的能源供需矛盾日益突出，可再生能源的优势越来越凸显出来，在其环保优势明显以及成本快速下降的趋势下，可再生能源发电系统逐渐形成规模，成为当今电网重要的成员之一，研究基于可再生能源的并网发电系统具有其重要意义[1-3]。可再生能源发出的电能(如光伏发电、风能发电)存在较大的波动，其电压等级一般比较低，常规逆变电路需要在直流侧加入升压稳压电路提高输入侧电压[4]，这样的两级拓扑电路降低了系统效率，增加了系统成本，Z源逆变器[5]的提出改变了这种模式，单级拓扑结构完成了升压稳压以及逆变的功能，其特有的阻抗网络可允许同一逆变桥臂同时导通而不必插入死区时间，提高了并网电能质量，因此Z源逆变器在可再生能源并网领域受到了广泛关注[6-7]。

目前，电流控制方式成了逆变器并网的主要控制方式[8-12]。针对Z源并网逆变的控制方式，文献[8-9]提出了电流滞环控制方法来实现单相或三相并网系统的单位功率因数并网，但滞环控制本身的延时性会对控制效果产生影响；文献[10-11]提出无差拍的电流预测控制方式降低了控制系统的延时性，但实验中没有验证输入电压波动系统能否稳定，其效果有待验证；文献[12]提出了比例谐振控制三相光伏逆变器并网，但控制效果仍依赖于电流传感器的精度；文献[13]提出了无电流传感器的间接控制方式，其单相并网效果较好，可并没有涉及到三相并网逆变器的研究。

本文提出一种无需电流采样环节的三相Z源并网逆变器的间接单周控制方式。通过检测Z源网络电容电压与设定电压比较产生直通占空比，来实现Z源网络的升压功能与稳压功能，有效抑制输入电压波动对系统造成的干扰；建立三相Z源并网逆变器的状态平均数学模型，运用单周控制思想推导出系统控制方程，实现单位功率因数并网。该控制方式的基础为系统的平均状态方程，运用单周控制原理，有别于传统的基于系统稳态数学模型的间接电流控制方式的，有效地改善了系统响应的速度。文章最后在理论推导的基础上，建立Matlab仿真模型验证了该控制方式的正确性与可行性。

1 系统状态函数的推导

三相Z源并网逆变器的主电路如图1所示，由于Z源网络特有的直通状态存在，所以其建模与控制和传统逆变器有着较大的区别。文献[14]将Z源网络后级逆变桥及负载等效为一个电流源，构建了Z源逆变器的简化电路模型。文献[5]通过Z源网络直通与非直通的等效电路计算出了Z源网络之间的电压关系：

(1)

式中：D0为直通占空比;uin为输入电压。

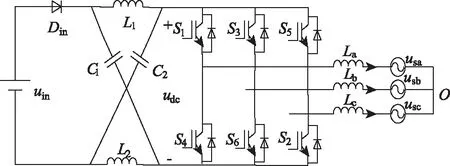
图1 Z源并网逆变器拓扑

在非直通状态下，逆变桥直流链电压udc为

(2)

由上式可以看出：通过调节直通占空比D0，便可以实现输入电压的升压与降压，不需要额外的中间级变换电路。

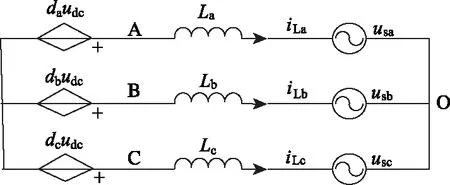
图2 三相逆变桥的平均电路模型

三相桥式逆变电路模型为系统函数的另一组成部分，文献[15]提出了如图2所示的三相逆变桥平均电路模型，通过文献[16]提出的一系列假设，可得A、B、C三点相对于N点的周期平均电压为

(3)

设La=Lb=Lc=Lf，则A、B、C三点相对于交流电网中性点O的电压值为

(4)

对于三相对称电网电压usa、usb、usc，有

usa+usb+usc=0

(5)

为实现单位功率因数并网，并网电流与电网电压成比例关系。定义控制并网功率参数K，则有

(6)

结合式(4)、(5)、(6)可得

uAO+uBO+uCO=0

(7)

根据平均电路模型，uAO、uBO、uCO又可表示为

(8)

结合式(4)、(7)、(8),再根据式(3)，可得

(9)

式(9)为开关占空比与直流链电压及电网电压之间的关系，其系数矩阵为一奇异阵，该方程无唯一解，其解可表示为

(10)

由0≤da≤1，得

(11)

在中小规模逆变电路中滤波电感取值Lf通常取毫亨级,并网参数K<0.01，电网频率为50Hz,可得

(12)

则K1的取值范围为

(13)

对式(10)进行适当变形，可得

(14)

式中：K为并网功率参数，可控制并网功率；K2为电压的采样系数。

式(14)为不考虑Z源网络情况下的单周控制方程，当考虑Z源网络的情下，由式(2)可得

(15)

式中：

(16)

式(15)为三相Z源并网逆变器的间接单周电流控制方程，控制系统根据输入电压变化及电网电压波动实时生产占空比da、db、dc，保证系统具有良好的抗扰动能力，提高系统稳定性及鲁棒性。

2 间接单周电流控制策略

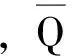
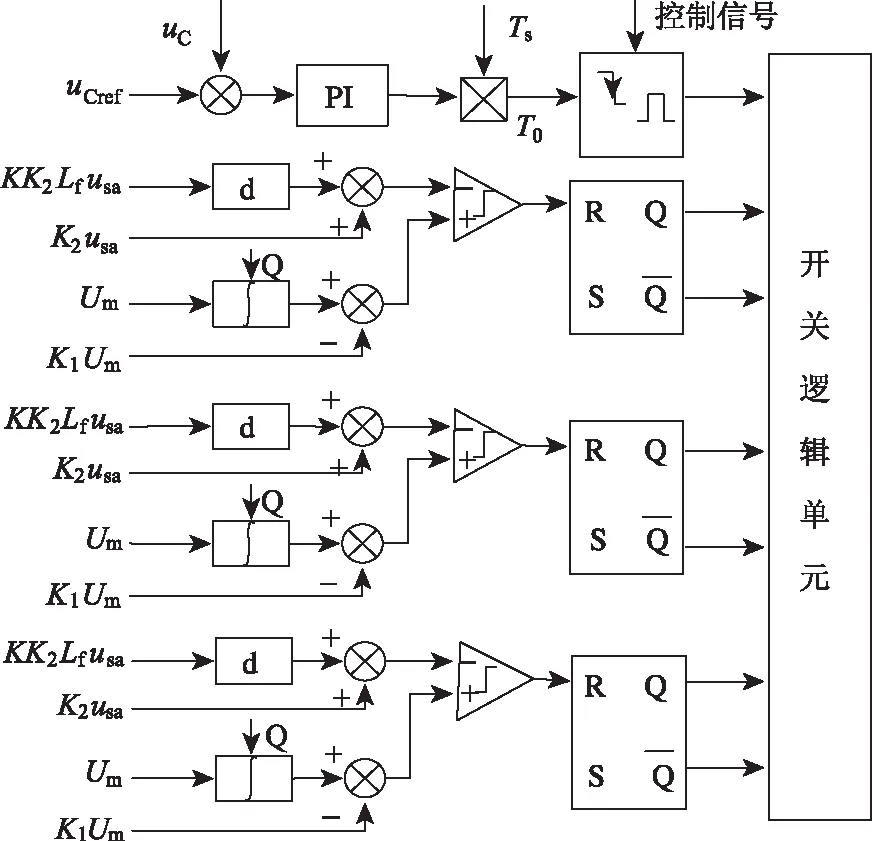
图3 控制电路结构

直通脉冲发生器[16]为Z源并网逆变器控制的重要组成部分。为保证阻抗网络电容电压uC恒定，将参考值uref与实际电压uC之差通过PI调节器，得到直通占空比D0，再与开关周期TS相乘得到直通脉冲时间，最终在控制信号的作用下产生脉冲信号。

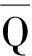
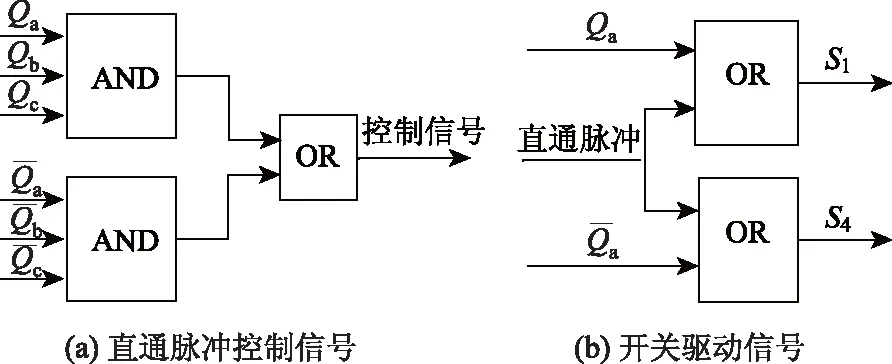
图4 控制电路结构

3 仿真验证

在提出理论推导的基础上建立了仿真模型，以验证所提出的三相Z源并网逆变器间接单周电流控制方式的可行性。仿真参数：直流输入电压uin=600V；阻抗网络电感L1=L2=1mH,电容C1=C2=470μF；电网电压为50Hz的220V三相对称电压，滤波电感Lf=1mH,R-S触发器时钟10kHz。

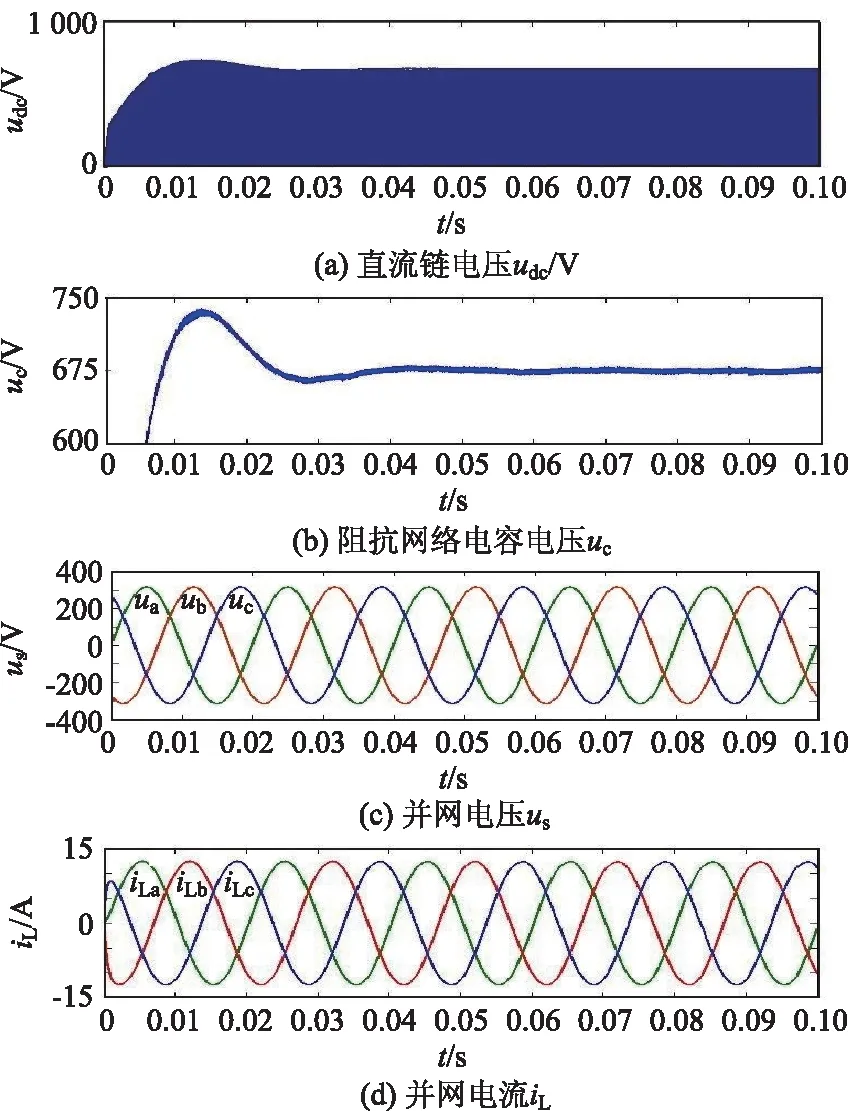
图5 Z源并网逆变器输出波形

设定Z源网络电容电压uC=675V，输出功率6kW，逆变器输出波形如图5所示，直流链电压udc和阻抗网络电容电压uC在启动的两个周期内可以达到稳定，超调量小于11%，其启动时电容上的冲击电压较小；输出电能实现了单位功率因数并网，并网电流的谐波畸变率0.81%，其频谱如图6所示。

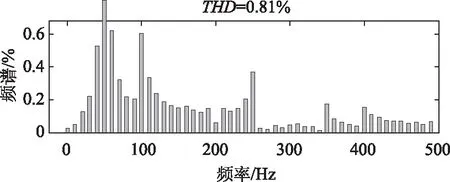
图6 并网电流iL频谱

在分析输出波形满足要求过后，改变输入电压可分析系统的稳定性，如图7所示，在0.9s时，直流电压uin=570V，并伴随有20V的电压波动，其并网电流iL几乎不受影响，电容电压经过一个工频周期的小幅波动后继续稳定在675V。

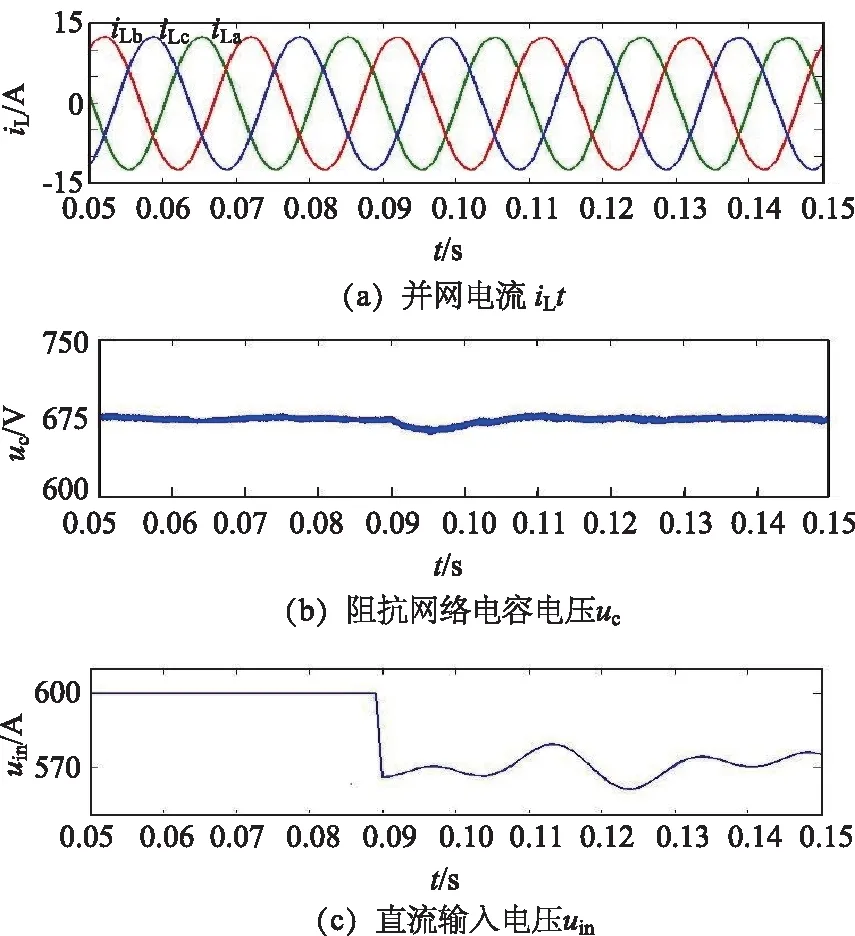
图7 直流输入电压突变时的输出波形

当改变输出功率时，其并网输出电流如图8所示，其电流能根据指令变化迅速达到新的稳定状态，其系统动态稳定性表现良好。

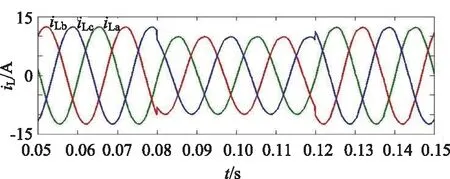
图8 改变功率参数后的电流波形

4 结束语

本文提出一种基于单周控制的三相Z源并网逆变器的间接电流控制方式。该控制方式建立在系统的平均状态方程的基础上，其动态特性优于传统间接控制方式，同时结合单周控制方式，具有动态响应快、稳定性较强、鲁棒性较优的特点，理论分析与系统仿真验证了上述结论。该控制方式实现方式简单，无需电流采样环节，成本低，在小功率可再生能源并网发电具有一定的实用价值。

[1] Ma Z, Wang H, Wu A, et al.An Intelligent Decision Support System for Residential Energy Consumption and Renewable Energy Utilization in Rural China[J]. Energy Source Part B-Economics Planning and Policy，2014(8):374-382.

[2] Chowdhury S H, Oo, A M T .Study on electrical energy and prospective electricity generation from renewable sources in Australia[J].Renewable & Sustainable Energy Reviews,2012(11): 6879-6887.

[3] Benli H .Potential of renewable energy in electrical energy production and sustainable energy development of Turkey: Performance and policies[J].Renewable Energy,2013(2)：33-46.

[4] Xue Yaosuo,Chang Liuchen,Kjaer S B,et al.Topologies of single-phase inverters for small distributed power generators:an overview[J].IEEE Transsctions on Power Electronics,2004(5):1305-1314.

[5] 彭方正，房绪鹏，顾斌等.Z源变换器[J].电工技术学报，2004,19(2):47-51.

[6] 杨水涛，丁新平，张帆等.Z源逆变器在光伏发电系统中的应用[J].中国电机工程学报，2008,28(17):112-118.

[7] 高奇. Z源逆变器的主电路研究[D].杭州：浙江大学，2005.

[8] 顾和荣，杨子龙，邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究[J].中国电机工程学报,2006,26(9)：108-112.

[9] 黄金军，郑建勇，尤鋆等.基于电流滞环控制的Z源三相光伏并网系统[J].电力自动化设备,2010,30(10): 94-99.

[10]吴凤江，孙秀冬，孙力等. 单相电压空间矢量无差拍控制Z源并网发电系统[J].中国电机工程学报，2010,30(31): 22-27.

[11]杨勇，阮毅，叶斌英等.三相并网逆变器无差拍电流预测控制方法[J].中国电机工程学报,2009,(33):40-46.

[12]王继东，朱雪玲，苏海滨等. 三相光伏并网Z源逆变器的比例谐振控制[J].电机与控制学报，2010,14(4):86-91.

[13]侯世英，肖旭，张闯等.Z源并网逆变器的间接单周电流控制策略[J].电机与控制学报，2011,15(9)：18-23.

[14]Loh P C,Vilathgamuwa D M, Gajanayake C J,et al. Z-source current-type inverters: digital modulation and logic implementation [C]. IEEE IAS, 2005: 940-947.

[15]Qiao Chongming,Smedley Keyue M. Unified Constant-Frequency Intergration Control of Three-Phase Standard Bridge Boost Rectifiers With Power-Factor Correction[D]. IEEE Trans. on Industrial Electronics,2003,50(1):100-107.

[16]肖旭.阻抗源并网逆变器的拓扑改进及其单周控制策略研究[D]. 重庆：重庆大学，2012.

(责任编辑：林海文)

Study of Indirect One-cycle Control Strategy Based on Three-phaseZ-source Grid-connected Inverter

DENG Qiang,YANG Yanxiang,TIAN Guo,YI Zhongyao,ZHAO Fan

(School of Electrical and Information Engineering , Xihua University , Chengdu 610039 , China)

In this paper, an indirect one-cycle control strategy based on three-phase Z-source network is proposed to solve the disadvantages of complex system and slow response in the conventional control mode. Combined with the relationship between input and output of Z-source impedance network, the mathematical model of three-phase Z-source grid-connected inverter is built based on state-average equations, and the control equation is deduced according to one-cycle control principle, which make inverter connect to power grid with unit power factor. Simulation results show that the three-phase Z-source grid-connected inverter based on one-cycle control can realize grid connecting with unit power factor in single power cycle (0.02s), the harmonic distortion rate of output current is less than 1%, and the output almost is not affected by input voltage fluctuation. Comparing with traditional Z-source grid-connected inverter, the indirect current control mode based on one-cycle control can achieve grid connecting with unit power factor rapidly in the absence of current sampling, which has such advantages as fast dynamic response, strong stability, and good robustness.

three-phase Z-source grid connecting; one-cycle control; state-average equation; unit power factor

1007-2322(2015)04-0074-05

A

TM4

西华大学研究生创新基金(yljj2014082)

2014-08-01

邓 强(1989—)，男，硕士研究生，研究方向为电力电子技术及其运用，E-mail:1029170956@qq.com；

杨燕翔(1963—)，男，教授，研究方向为现代信号处理及其运用，E-mail:yyx@mail.xhu.edu.cn；

田 果(1992—)，女，硕士研究生，研究方向为分布式电源的并网，E-mail:tianguoxihua@163.com；

易忠尧(1989—)，男，硕士研究生，研究方向为配电网络规划，E-mail:414325058@qq.com；

赵 帆(1989—)，男，硕士研究生，研究方向为风电并网技术，E-mail:1760460184@qq.com。