改进霍尔三维视角下智能电网差异化评价研究

喻小宝，谭忠富

(华北电力大学经济与管理学院， 北京 102206)

改进霍尔三维视角下智能电网差异化评价研究

喻小宝，谭忠富

(华北电力大学经济与管理学院， 北京 102206)

对于智能电网差异化评价问题，文章通过分析将综合评价差异化问题转变为权重差异化问题，并对传统霍尔三维模型进行改进，将权重差异化细化到四维模型中，考虑了不同地区由于资源不同而导致的智能电网建设侧重点不同对权重的影响，最后结合脱钩指数的理论对不同地区的智能电网建设评价情况展开研究。文章以北京、天津和河北为研究对象，探讨了模型在智能电网差异化评价中的应用。结果表明，四维模型结合脱钩指数能够合理地对不同地区的智能电网建设进行差异化评价。

差异化；霍尔三维；脱钩指数；权重；综合评价

0 引 言

当前，国内外对于多指标综合评价的研究很多，国内学者易平涛[1]等针对多指标动态奖励或惩罚的评价问题，提出运用修正因子和修正函数对多指标进行纵向与横向修正的多指标动态综合评价修正方法；刘鸿雁[2]认为当前多指标综合评价方法发展不完善，在指标体系构建、评价方法选择、数据标准化等操作程序中存在问题，并提出相关建议；刘敦楠[3]等利用TOPSIS法对被评价对象连续期间的指标值进行动态处理，改进了动态综合评价矩阵，使评价结果体现出被评价对象各个指标连续期间的综合动态水平。国外学者[4]将多指标评价运用到能源效率评价上，采用AHP与三维结构模型对指标评价进行分析；还有一些学者[5]采用了其他的方法论对多指标综合评价展开研究。

然而，对于多指标差异化评价的研究并不多，大多数学者都是仅仅从单个指标的视角进行分析而缺乏系统化研究。段赞君[6]通过差异化的5个部分品牌、产品、营销、服务和其它方面的分析，由客户打分和专家打分两个角度，用指标分值法和层次分析法对公司差异化开展研究；曾鸣等[7]采用改进型层次分析法对电力客户按用电类别分别进行信用与风险等级评价，根据评价结果制定电费回收及欠费风险防范的差异化服务措施,并对电力客户的信用结构及信用发展趋势加以分析。而且，对智能电网建设评价的研究以静态评价为主，评价的标准过于单一，导致评价结果缺乏科学性与可比性。本文提出一种兼顾地域差异和贡献差异的动态评价思路。

本文基于霍尔三维视角，并对其进行改进，构建差异化评价四维结构图，从系统化角度对差异化分析评价。差异化主要体现在评价权重的部分，通过贡献差异性、空间差异性来计算权重，反映出评价的差异性；通过对脱钩指数的分析来反映评价的时间差异性。最后，本文以北京、天津与河北为研究对象，探讨了智能电网差异化评价的合理性。

1 霍尔三维理论及其改进

霍尔三维结构理论[8-9]是由美国贝尔电话公司通信工程师和系统工程专家霍尔于1969年提出来的，也称为霍尔方法论。霍尔三维结构使用时间维、逻辑维和知识维3个维度组成的立体空间结构，概括地表示出系统工程的不同阶段、不同步骤以及所涉及的专业知识。霍尔三维结构将系统工程活动按照时间维分为7个阶段，按照逻辑维分为7个步骤，同时再考虑相关的专业知识。霍尔三维结构为解决系统问题，特别是大型复杂的系统问题提供了一种新的思维方法。作为运用系统工程来解决实际问题的方法论基础，霍尔三维结构已经在社会、经济、军事、教育、区域规划、农业、物流等各个领域得到了广泛采用。

然而，霍尔三维结构应用到智能电网综合差异化评价中需要对其进行改进，才能满足差异化评价的要求。首先，构建改进的四维模型，主要由4个维度组成，形成一个立体空间结构，主要分为属性维、贡献维、空间维和时间维4个维度。其中，属性维是指智能电网动态评价指标体系中的评价指标；贡献维是指不同指标反映的智能电网建设贡献不同，也反映不同地区对智能电网建设的贡献不同；空间维是指智能电网动态评价中反映出不同地域间差异性的维度；时间维是指智能电网动态评价中反映出时间差异性的维度。将属性维、贡献维、空间维和时间维结合在一起就可以得到智能电网动态评价的四维模型，如图1所示。

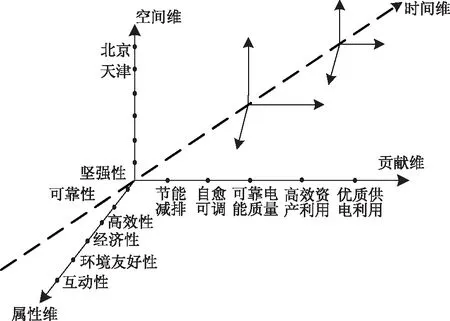
图1 智能电网动态评价四维模型

属性维：智能电网动态评价中将评价指标分为六大类，分别是坚强性、可靠性、高效性、经济性、环境友好性和互动性。每一类指标下设二级指标和三级指标，具体表1所示。

贡献维：根据不同指标反映的贡献不同以及不同地区的贡献不同将四维结构中的贡献维分为5个部分，分别是节能减排贡献、自愈可调贡献、可靠电能质量、高效资产利用和供电优质服务。

空间维根据评价的对象不同而有所变动；时间维根据评价时间的不同也有所改变，此处不再赘述。

2 差异化权重计算的原理与算法

对于智能电网差异化评价，本文提出的方法是对评价计算权重的差异化进行研究，通过权重的差异化来体现不同地区的差异化。首先，根据不同属性对智能电网建设的贡献不同来计算属性维到贡献维的映射矩阵，即第一次修正矩阵。考虑到研究的可行性，本文选取二级指标进行权重修正。

不同指标对智能电网建设的贡献不同，根据贡献大小对指标间关系进行对比，比较规则如下：

以αij表示指标i与指标j比较值，当i=j时，αij=1。属性间比较规则如表2所示。

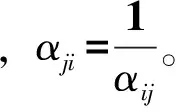
得到判断矩阵如下所示。

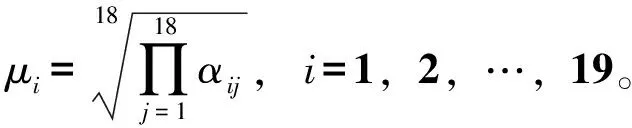
k=1,2,…,5

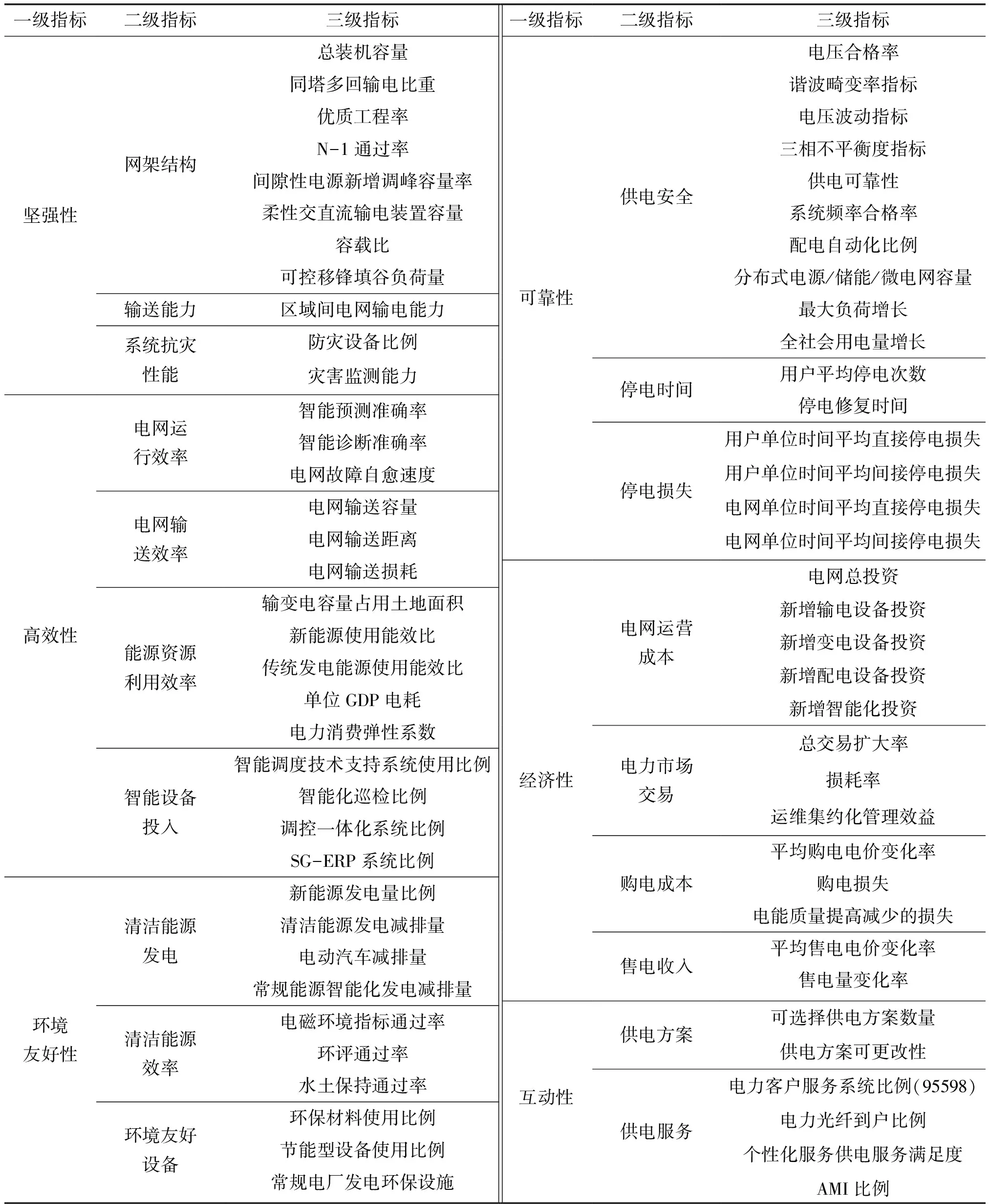
表1 智能电网动态评价指标体系

表2 属性比较规则

综述所述，可以得到贡献维对属性维的第一次修正矩阵，如下：

在得到属性维对贡献维的映射矩阵后，还需要考虑不同地区的电网建设目标不同，即地域对不同贡献维度的差异性，构建地区对贡献维度的第二次修正矩阵，结合属性维对贡献维的映射矩阵，得到最终的修正矩阵。

首先，设定研究对象有n个地区，针对每个地区进行不同贡献维度之间的比较，得到判断矩阵。以某一地区为例，研究该地区对不同贡献维度的侧重关系，得到该地区的判断矩阵，如下：

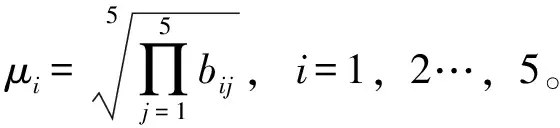
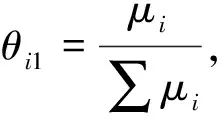
同理，对其他地区进行相同运算处理，就可以得到各地区的第二次修正矩阵，如下：

在标准权重的基础上，结合两次修正矩阵，计算得到修正权重，修正矩阵计算如下：

φ19×n=β19×5·θ5×n=

易知标准权重矩阵是一个对角矩阵，假定为κ19×19，则二级指标的修正权重计算如下：

由此就可以得到不同地区不同二级指标的修正权重，一级指标的修正权重在二级指标修正权重的基础上进行整合，主要根据同一个一级指标下的二级指标权重之和占整个二级指标权重之和的比重作为一级指标的修正权重。

3 脱钩指数的原理与算法

脱钩指数[10-12]可以有效反映针对某一指标不同地区的发展情况，本文采用脱钩指数的理念，对通过差异化权重计算得到的评价值进行深入研究，根据各地区各指标脱钩指数的走势情况，对各地区坚强智能电网建设的差异性进行再评价。

假定坚强性下设的三级指标m年内数据已知，设定为xijt,i=1,2,…,11;j=1,2,…,n;t=1,2,…,m表示第j地区第i个指标第t年的数据。

结合三级指标的标准权重计算出二级指标评价值，设定为kijt,i=1,2,3;j=1,2,…,n;t=1,2,…,m，表示第j地区第i个二级指标第t年的评价值。

结合二级指标的修正权重计算出坚强性m年的评价值，设定为yijt,i=1;j=1,2,…,n;t=1,2,…,m，表示第j地区坚强性第t年的评价值。得到一个坚强性评价矩阵，如下所示：

根据坚强性评价矩阵可以计算各地区各时间段的脱钩指数，计算如下：

由此就可以得到各地区各时间段的脱钩指数，根据脱钩指数大小，判断各地区坚强性的发展情况，判定规则如下：

4 算例分析

4.1 修正权重计算

本文选取3个地区2009～2013年的实际数据进行计算分析。首先计算修正权重，修正权重是在基本权重的基础上考虑贡献差异性和地区差异性得到的，对于基本权重的设定，这里采用均值的方法，即所有指标的重要程度相同。根据专家组意见，给不同贡献维度下不同二级指标间重要程度关系进行评分，收集评分结果，进行处理，得到贡献维对属性维的修正矩阵，如表3所示。

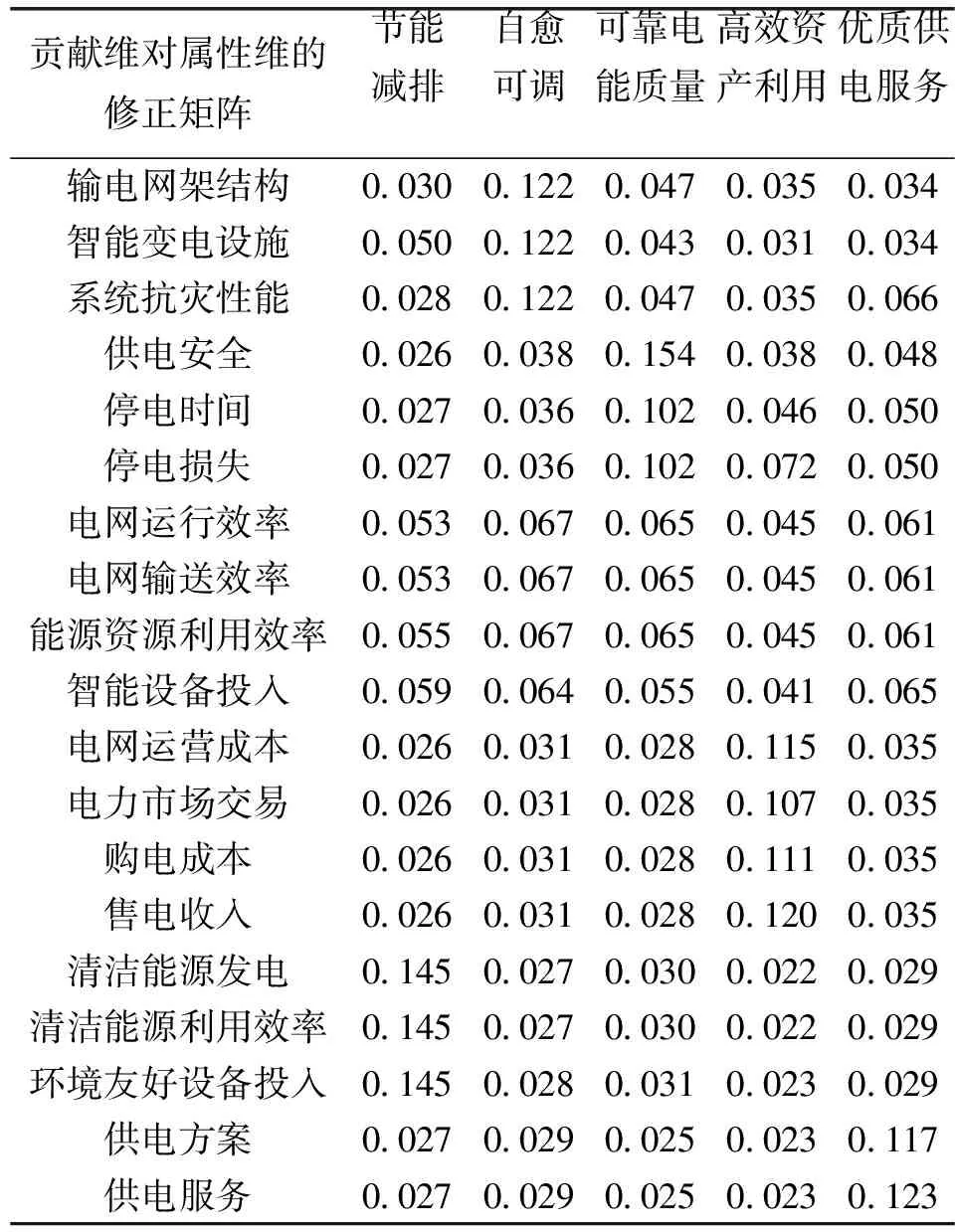
表3 贡献维对属性维的修正矩阵

同样根据专家组建议，给不同地区维度下的不同贡献目标之间的偏重程度关系进行评分，收集评分结果，得到空间维对贡献维的修正矩阵，如表4所示。

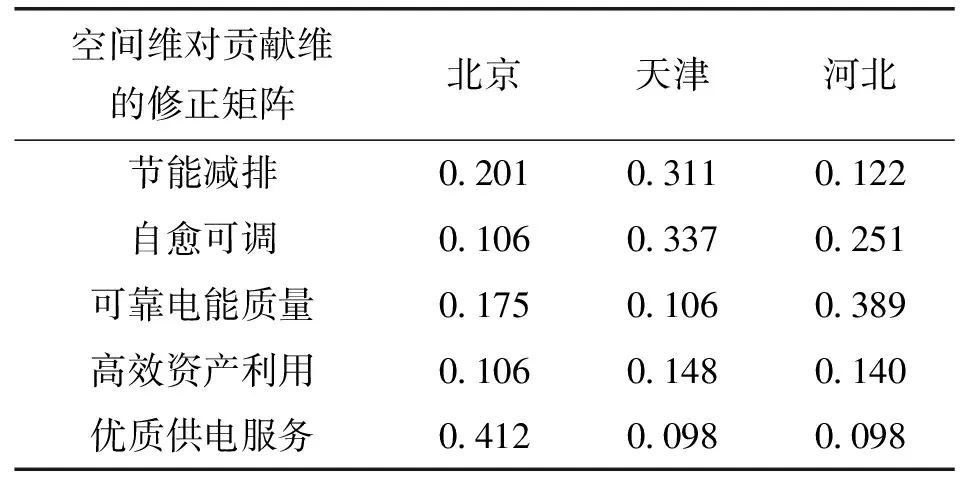
表4 空间维对贡献维的修正矩阵

将贡献维对属性维的修正矩阵与空间维对贡献维的修正矩阵相乘，得到最终的修正矩阵；再将修正矩阵与基本权重的对角矩阵相乘，就可以得到修正权重，如表5所示。

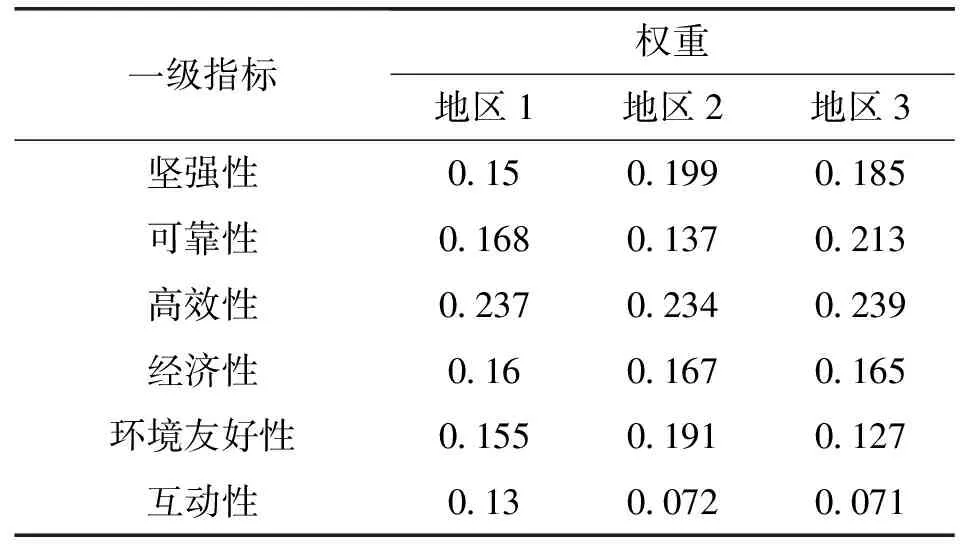
表5 修正权重

从修正权重可以看出，各地区的一级指标权重明显不同，这与各区域本身存在的差异性有关，有些地区发电资源丰富，因而更加偏重智能电网的电源建设，而有些地区属于用电重点区域，因而更加偏重智能电网的需求侧建设，还有些地区属于电能输送的重点区域，因而更加偏重智能电网的输电安全稳定性建设。根据不同地区智能电网建设的偏重不同，不同指标对贡献维的不同，给予不同的权重，才能不失公平性，本文根据不同地区的地域特点所得到的修正权重更加符合公平性原则。

4.2 综合评价分析

收集各地区三级指标2009～2013年的实际数据，首先进行标准化处理，再结合修正权重进行综合评价值计算，根据计算过程，可以得到各一级指标的评价值以及各地区的综合平均值，具体如表6所示。

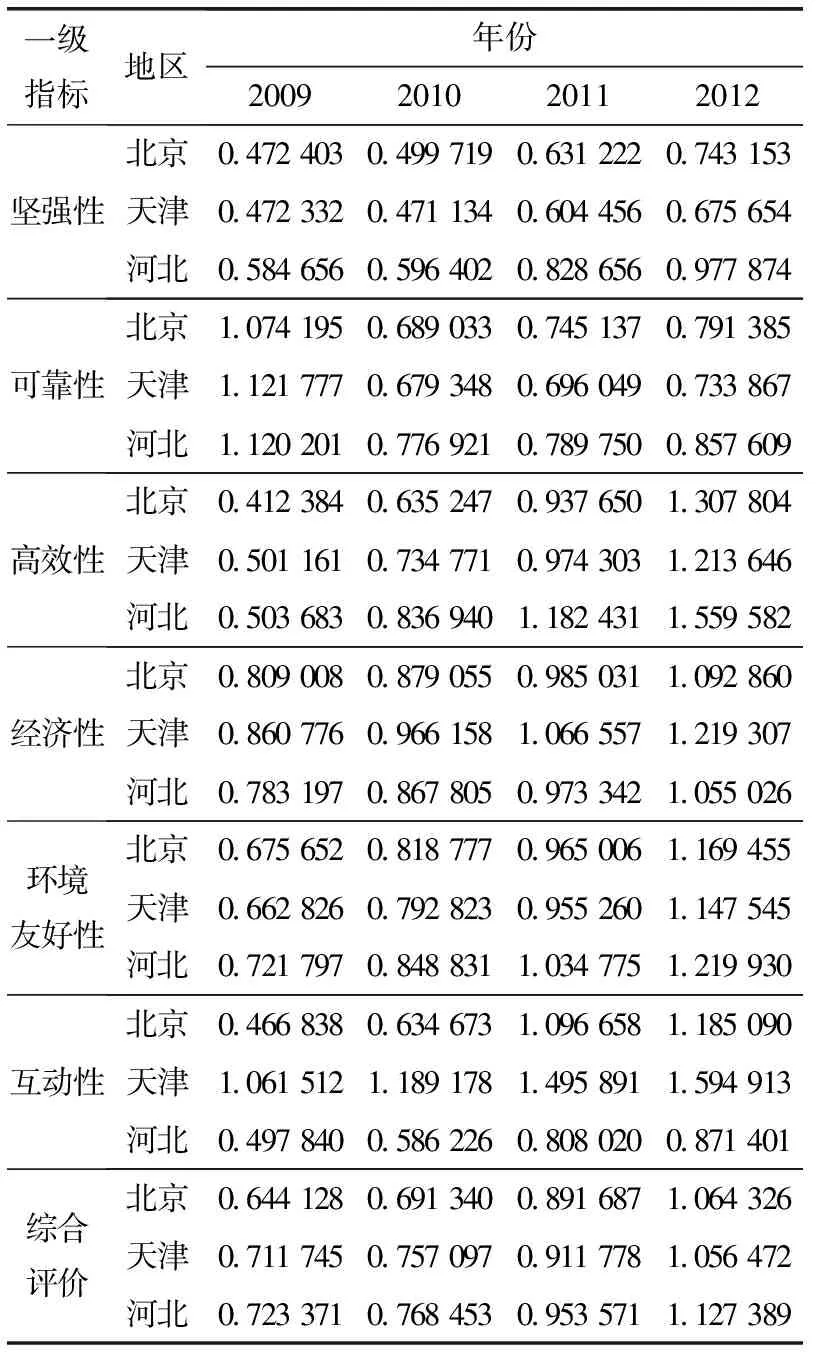
表6 一级指标评价值

图2 各地区综合评价值走势

从各一级指标的评价值来看，3个地区各有所长，北京在坚强性和环境友好性3个方面都占有优势；天津在经济性和互动性方面占有优势；河北在可靠性和高效性方面占有优势。但是从综合评价值来判断，河北一直以微弱优势保持领先，这表明河北虽然在智能电网建设各方面并不是保持第一，但是各方面建设都有所发展，导致在智能电网建设综合评价时处于第一的位置。接下来本文选取坚强性和可靠性分析各地区智能电网建设各方面的发展情况。

4.2.1 坚强性

根据脱钩指数的计算公式，对得到的各地区坚强性指标评价值进行脱钩指数计算，并根据计算结果对各地区智能电网坚强性发展情况进行分析。各地区坚强性指标的脱钩指数散点图如图3所示。

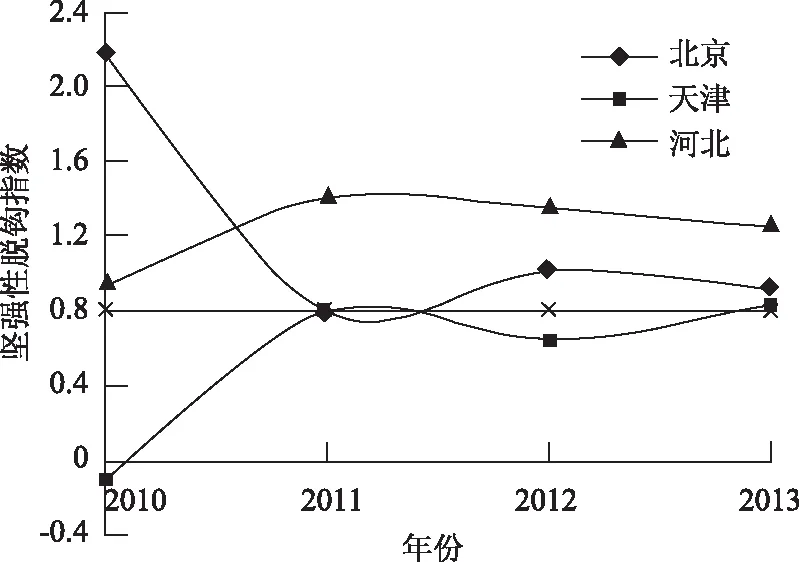
图3 各地区坚强性脱钩指数走势

从各地区的脱钩指数分布情况来看，结合脱钩指数的分布情况和坚强性评价情况，发现尽管北京的坚强性评价值较高，但是历年的发展情况一般，河北的评价值虽然不高，但是历年发展情况最佳，这表明河北在智能电网坚强性建设方面的进步更多一些。

4.2.2 可靠性

各地区可靠性指标的脱钩指数散点图如图4所示。

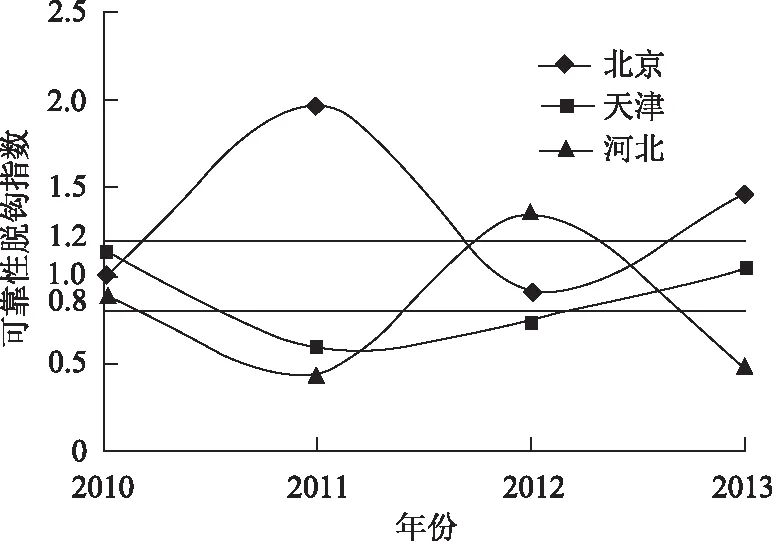
图4 各地区可靠性脱钩指数走势

从各地区的脱钩指数分布情况来看，说明北京的智能电网可靠性建设基本处于较好的发展状态；天津的可靠性建设脱钩指数数据表明天津的可靠性建设情况并不乐观；河北的可靠性建设脱钩指数的波动幅度较大，说明河北的可靠性建设并不稳定，与智能电网总体建设步伐不一致。

4.2.3 综合分析

由于各地区的智能电网建设侧重点不同，导致对于不同功能建设的发展情况不同，需要对各地区的智能电网综合建设评价值进行脱钩指数分析，各地区的脱钩指数散点图情况如图5所示。

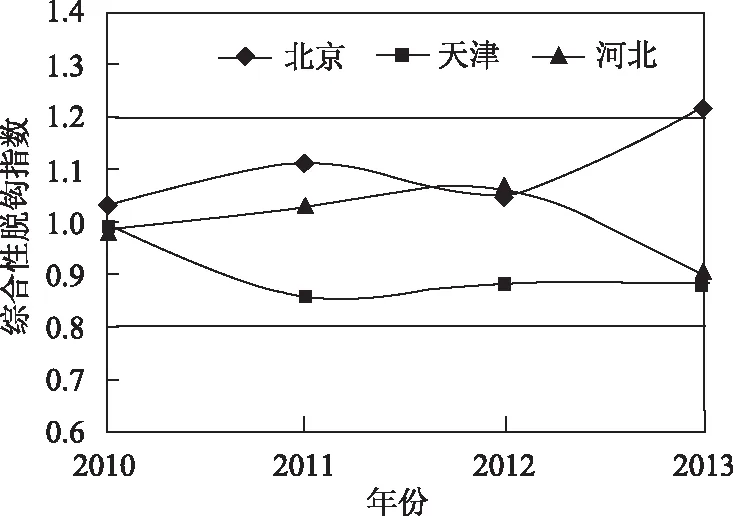
图5 各地区综合评价脱钩指数走势

从各地区的脱钩指数来看，北京的智能电网建设发展情况最优；天津的智能电网建设脱钩指数处于落后地位；河北的智能电网建设发展情况较好。

结合各地区的智能电网综合评价值和智能电网建设脱钩指数分布图发现，河北的智能电网综合评价值最高，但是其近年来的发展步伐不是最快；北京的智能电网综合评价值虽然较低，但是其发展步伐最快，所以出现2013年的综合评价值基本等于河北的综合评价值；天津智能电网建设发展处于平均水平。

5 结 论

本文对智能电网的差异化评价进行了探讨，对传统霍尔三维模型进行改造，构建智能电网差异化评价四维模型，通过权重的差异化来体现不同地区的智能电网差异化评价。不同地区资源不同，对智能电网建设的偏重点不同，通过对权重的调整来将智能电网差异化评价合理化。最后结合脱钩指数的理论，对不同地区智能电网建设的发展情况进行了分析及合理评价。

以北京、天津和河北为评价对象，采用本文提出的四维模型进行智能电网建设评价。根据计算得到的权重发现，不同地区的各指标权重明显不同，结合实际情况表明权重设计合理。实证分析表明，不同地区智能电网建设发展不同步，综合评价值显示北京与河北在智能电网建设总体上更优。

[1] 易平涛,张丹宁,郭亚军,等.动态综合评价中的无量纲化方法[J]. 东北大学学报：自然科学版,2009(6):889-892.

[2] 刘鸿雁，郝惠茹，孔峰．对时序多指标业绩综合评价方法的改进[J].电力科学与工程，2008(4)：35-37.

[3] 刘敦楠，陈雪青，何光宇，周双喜.电力市场评价指标体系的原理和构建方法[J]. 电力系统自动化，2005(23)：2-7+14.

[4] Zhao Jing， Wu Yong， Zhu Neng. Check and evaluation system on heat metering and energy efficiency retrofit of existing residential buildings in northern heating areas of China based on multi-index comprehensive evaluation method[J].ENERGY POLICY. 2009(37)：2124-2130.

[5] 赵凯，门可佩，蒋勇. 具有纵向可比性的三维动态灰关联模型及其应用[J]. 统计与决策，2014(1)：69-71.

[6] 段赞君. V北京分公司差异化竞争战略评价与对策研究[D].北京：北京工业大学，2012.

[7] 曾鸣，王鹤，王涛. 电力客户信用评价与差异化服务技术支持系统[J]. 电力需求侧管理，2007(1)：19-22.

[8] 毕翼，陈刚. 基于霍尔三维结构的绩效审计评价指标体系设计思路[J]. 中国内部审计，2014(1)：58-61.

[9] 王银华. 基于霍尔三维结构理论的高速公路投资项目评价体系的研究[J]. 交通标准化，2008(11)：109-113.

[10]肖丽群，吴群. 基于脱钩指数的2020年江苏省耕地保有量目标分析[J]. 资源科学，2012(3)：442-448.

[11]欧阳文喜，谢德泳，张天昊. 中国能源消耗与经济增长——基于IPAT脱钩指数的脱钩分析[J]. 中南财经政法大学研究生学报，2013(1)：21-27.

[12]孙睿. Tapio脱钩指数测算方法的改进及其应用[J]. 技术经济与管理研究，2014(8)：7-11.

(责任编辑：林海文)

Differentiated Evaluation of Smart Grid in the Improved HallThree-dimensional Perspective

YU Xiaobao, TAN Zhongfu

(School of Economics and Management, North China Electric Power University, Beijing 102206，China)

In this paper, through analyzing, the issue of comprehensive evaluation difference is turned into the question of the weight difference as to the differentiated evaluation of smart grid. In addition, the traditional Hall three-dimensional model is improved, the weight difference is elaborated into four-dimensional model, and the effects of different construction emphasis for smart grid caused by different sources in different regions on weights are taken into account. In the end, the construction evaluation of smart grid in different areas is studied according to decoupling index theory. Taking Beijing, Tianjin and Hebei power grids as examples, the application of model to differentiated evaluation of smart grid is discussed. The results show that the combination of four-dimensional model and the decoupling index can be used to reasonably evaluate smart grid construction in different regions.

differentiation; Hall three-dimensional model; decoupling index; weight; comprehensive evaluation

1007-2322(2015)04-0042-07

A

TM7

北京市产学研联合培养研究生共建项目

2014-09-07

喻小宝(1989—)，男，博士研究生，研究方向为电力经济运行与能源规划，E-mail:yuxiaobao1222@163.com；

谭忠富(1964—)，男，教授，博士生导师，研究方向为电力经济与能源经济等, E-mail:tanzhongfu@sina.com。