计及电压稳定裕度的配电网光伏发电选址与定容
2015-05-05白晓清吴雪颖李佩杰杨秀菊
白晓清,吴雪颖,李佩杰,杨秀菊
(广西电力系统最优化与节能技术重点实验室(广西大学),广西南宁 530004)
计及电压稳定裕度的配电网光伏发电选址与定容
白晓清,吴雪颖,李佩杰,杨秀菊
(广西电力系统最优化与节能技术重点实验室(广西大学),广西南宁 530004)
本文针对光伏出力的随机性和负荷的波动性,考虑光伏出力及负荷在不同状态下发生的概率,提出了一种多场景光伏发电-负荷混合概率模型。采用电压灵敏度分析法寻找电压支撑点,作为光伏发电接入的候选节点集,提高光伏选址的效率。以改进VPII指标为目标函数,将多场景光伏发电-负荷混合概率模型加入功率潮流平衡方程,建立光伏发电的选址和定容模型。最后,以IEEE14辐射型配电网系统为算例,验证了本文所提模型的合理性和有效性。仿真结果表明,合理选择光伏的接入位置和容量,能够有效提高配电网的电压稳定裕度,提升其稳定性并降低网损。
光伏发电;配电网;改进VPII指标;光伏发电-负荷混合概率模型;候选节点集;电压稳定
0 引 言
伴随能源紧缺和环境污染的进一步凸显,传统发电技术的缺陷日益突出,可再生能源发电的优势愈来愈引人注目。光伏发电属于可再生能源发电技术之一,主要优势体现在零污染、零消耗以及近距离供电,节约输电线路投资,降低输电损耗。目前,分布式光伏发电的并网规模可分成:大规模光伏发电站、小规模屋顶及建筑光伏发电。大量分布式光伏发电并入配电网中,使其复杂性大大增加,改变其潮流分布,给配电网的电压稳定带来了严峻的考验。文献[1]研究表明,当分布式电源渗透率在1%~5%范围时,对电网的影响不明显;当达到20%~30%时,对网络损耗、电压稳定裕度、潮流分布将产生显著的影响。文献[2]指出配电网的电压不稳定问题会影响相应的输电网络,如,1997年巴西某电力系统由于配电网电压不稳定而导致了大停电事故。
随着经济快速发展,配电网的负荷急剧增长,配电网运行更加接近电压不稳定边界。文献[3]指出配电网电压稳定裕度下降的主要根源是负荷增长。分布式电源合理接入配电网近距离向负荷提供功率,有利于均衡系统节点负荷,提高电压稳定裕度。然而,不合理的分布式电源接入会造成电压稳定裕度下降,最终恶化配电网的运行环境。
因此,在配电网运行及其扩展规划中,有必要研究分布式电源的选址和定容对配电网的电压稳定裕度的影响。文献[4]研究了不同类型风机的安装位置和出力情况对微网电压质量的影响。文献[5-6]提出计及静态电压稳定约束的分布式电源规划模型,指出分布式电源的选址和定容是影响系统静态电压稳定性的两个重要因素。如果并网位置选择不当,较小的分布式电源容量便可恶化系统的静态电压稳定性。文献[7]指出合理的风电并网容量有利于提高地区电网电压水平。如果接入容量不合理,会导致有功功率逆向传输,线路损耗高,甚至个别线路的传输功率越限、电压稳定性降低。文献[8]提出一种电网安全性综合指标,分别从风电场并网、切出和间歇输出功率的3种情况来分析风力发电对配电网电压稳定性的影响。上述文献所建立的分布式电源对电压稳定评估模型中,都未考虑分布式电源出力和负荷的随机性。此外,对于分布式电源的选址问题,通常以系统的所有节点或者固定某几个节点作为候选接入点。
本文首先综合考虑光伏出力及负荷在多个状态下发生的概率,建立了多场景光伏发电-负荷混合概率模型。然后运用电压灵敏度分析,选择灵敏度较高的节点为候选节点集。以改进VPII(voltage profile improvement index)指标衡量电压稳定裕度,并作为目标函数。同时将多场景光伏发电-负荷混合概率模型加入功率潮流平衡方程中,考虑变电站容量、节点电压、节点渗透率、 支路传输电流、系统渗透率约束,建立了光伏发电选址与定容对电压稳定裕度影响的模型。最后,以IEEE14辐射型配电网系统作为算例进行仿真,结果表明,合理选择光伏发电的接入点和容量,可提高配电网的电压稳定裕度、降低系统的网损。
1 多场景光伏发电负荷混合概率模型
求解随机规划问题的过程中,要求对随机变量进行详细描述,需要把随机优化模型转化成相应的确定性等价模型,通常运用离散概率分布形式来表示连续概率分布的随机变量。本文基于场景发生概率的决策树方法[9],构建多场景光伏发电-负荷混合概率模型,将配电网的连续运行状态分成多个离散场景。多场景光伏发电-负荷混合概率模型涵盖了多个状态的负荷和光伏出力,可有效描述光伏出力和负荷的随机性特征。
1.1 光伏模型
为了描述光伏模块输出功率的随机现象,光伏模型建模采用Beta分布函数,相应光伏功率输出的概率密度函数f(PPV)为
(1)
式中:α、β为Beta分布函数形状参数;Pmax为方阵最大输出功率;τ为Gamma函数。
光伏输出的功率近似为
PPV=ηAs
(2)
式中:η为光电转换效率;A为光伏阵列面积;s为实时光照强度。
根据文献[10],将某时段的光伏出力 [0,PPV]区间均分成Npv个离散的功率值,每个区间状态对应的概率为
(3)
式中:Psi(GPV)为对应功率状态区间(PPV1,PPV2)光伏阵列功率输出的概率。
1.2 容量因子CF
容量因子是衡量光伏模块有效利用率的指标。容量因子越高,说明光伏模块在该安装点上利用率越高,平均输出功率越大。每小时的平均输出功率等于该时段所有状态的输出功率与对应状态的概率乘积之和。代表日的平均输出功率可以根据每小时平均输出功率计算得到,年平均输出功率可以依据类似方法计算得出。容量因子可定义为平均输出功率占额定功率的百分比。
(4)
(5)
式中:PPVi为第i场景光伏阵列发出有功功率;Psi(GPV)为第i场景发生的概率。
1.3 负荷模型
日常生活中工业、商业、生活等不同类型的用电负荷的变动规律及全年的季节性影响决定了负荷也属于一个随机变量,为了模拟负荷的随机特性,测试系统的负荷曲线为文献[11]所提的IEEE-RTS系统每小时负荷曲线。运用聚类技术[12]将负荷划分为Nload个不同水平的负荷以及对应的概率PNload,文中将负荷分成10状态,即Nload=10,详细情况如表1。
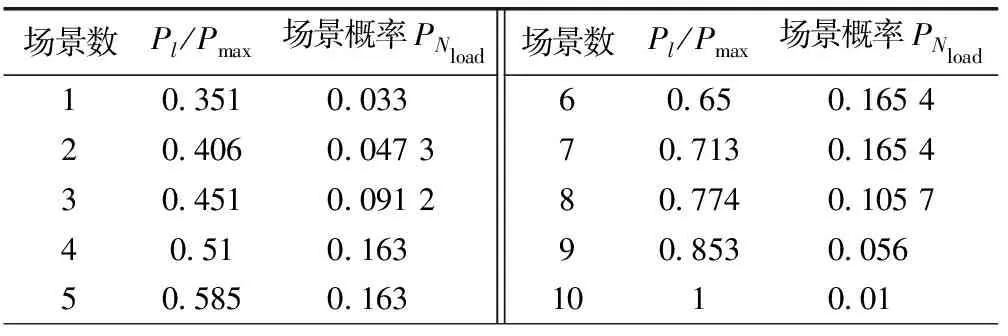
表1 负荷场景划分情况
1.4 多场景光伏发电-负荷混合概率模型
根据光伏出力以及负荷模型产生多场景光伏发电-负荷混合概率模型。假设光伏发电出力状态以及负荷状态之间是独立的,每个组合状态的概率Prn(Cn)通过两个对应状态概率卷积得到:
(6)
多场景光伏发电-负荷混合概率模型包括了所有分布式光伏发电出力和负荷的组合数,含多个场景,表达如下:
(7)
式中:R为完整的多场景光伏发电-负荷混合概率模型;M为总的场景数;Prn(Cn)为单列M行数组,表示对应矩阵C的每个场景的相应发生概率;C为M行g列的矩阵,g=1时,为每个场景光伏阵列发出有功功率占其额定功率的百分比;g=2时,为对应每个场景的负荷水平。
图1是运用场景发生概率的决策树方法生成的多场景光伏发电-负荷混合概率模型的框架图。多场景光伏发电-负荷混合概率模型包含总的场景数M=NpvNload,文中的算例是将光伏出力以及系统的负荷水平分成10个不同状态,故M=100。
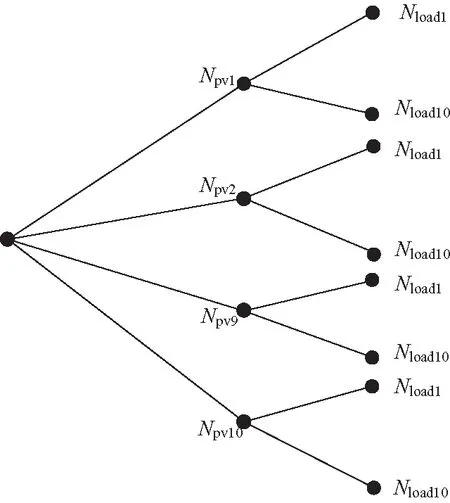
图1 多场景光伏发电-负荷混合概率模型结构图
2 候选节点集
配电网传统供电模式为单电源辐射供电,电压平衡靠首节点(变电站)维持。分布式光伏发电接入打破了这种模式,配电网由单一电源供电向多电源供电模式转变。为提高系统电压稳定水平,采用电压灵敏度分析法[13-15]选出灵敏度较高的节点作为分布式光伏发电可接入的候选节点。具体方法如下:
在稳态情况下,电力系统中功率、电压之间关系的非线性方程表示为
(8)
式中:ΔP为节点有功功率注入的变化量;ΔQ为节点无功功率注入的变化量;Δθ为节点电压相角的变化量;ΔU为节点电压幅值的变化量;JPθ、JPV、JQθ、JQV分别为P、Q对θ、U的偏微分矩阵。雅克比矩阵的各元素给出了功率和节点电压之间的灵敏度,而系统的电压稳定性受有功功率和无功功率影响。假设在每个运行点,无功负荷是恒定的,则无功负荷增量应为零,上式可变为
(9)
ΔU=(JRPV)-1ΔP
(10)
式中:JRPV是降阶雅克比矩阵,具体为
(11)
根据分布式光伏发电注入有功功率,由公式(9)的降阶雅克比矩阵可以得到电压幅值的变化量,即各节点的电压灵敏度。灵敏度较高的节点为系统中起到电压支撑作用的节点。为提高系统的电压稳定裕度,选择电压灵敏度较高的节点作为分布式光伏发电的候选接入点。
3 光伏发电对电压稳定裕度影响的模型
3.1 电压稳定裕度与改进VPII指标
从当前运行点按指定负荷增长方向增加至电压崩溃,电压稳定裕度定义为电压崩溃点与当前运行点的功率差。该距离作为衡量电力系统电压稳定水平的一个指标,反应了当系统受到负荷及故障扰动时,维持电压稳定的能力。在传统连续潮流的电压稳定裕度模型中考虑分布式光伏发电的选址和定容,如果顾及光伏出力和负荷在不同状态发生概率,会增加问题的复杂度,难于求解。为了分析光伏发电接入对配电网的电压稳定裕度的影响,本文提出采用改进的VPII指标作为衡量光伏发电接入系统后对电压分布改善的尺度。将光伏接入电压灵敏度较高的节点,通过改善该节点区域的电压分布,提升系统的电压稳定,进而提高系统的电压稳定裕度。目前大部分分布式光伏发电的运行功率因数都为1,这是为了避免电压调节装置连接到系统受分布式电源发出无功功率的干扰[16-17]。因此,本研究假设所有光伏发电的运行功率因数均为1。
3.2 改进VPII指标的目标函数
本研究通过合理选择光伏发电的接入点和容量来改善配电网的电压分布,提高其电压稳定裕度。文献[18]提出一种改善配电网电压分布指标(voltage profile improvement index,VPII),VPII指标可以通过光伏发电接入前的UP,withoutDG与接入后的UP,withDG电压分布比值来量化,如
(12)
(13)
式中:Vi为节点电压;Li为节点的负荷;ki为各节点的权重因子;m为系统节点数。
本文根据以上定义进行了扩展,提出含有混合概率的改进VPII指标,该指标同时考虑了负荷和光伏出力的不确定性,为
(14)
如果模型求解结果Uindex>1即光伏发电的接入点以及容量有利于提高电压分布;Uindex=1即光伏发电的接入点以及容量对电压分布没有任何影响;Uindex<1即光伏发电的接入点以及容量对电压分布产生消极影响。
改进VPII式中的ki为特定节点负荷Pi,n占总负荷PTD,n的比值
(15)
ki应满足:
(16)
通过分析VPII指标,可以直观了解到光伏发电接入系统后,对系统电压分布的改善程度。此外,ki是根据不同节点负荷的重要程度设置的,这意味着节点负荷越重,权重因子值就越高。
3.3 约束条件
3.3.1 含光伏发电-负荷混合概率模型的潮流功率方程
PGn,i+C(n,1)PPVi-C(n,2)PDi=
(17)
QGn,i-C(n,2)QDn,i=
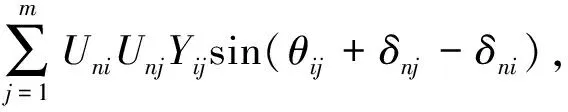
(18)
式中:PGn,i为第n场景节点i注入的有功功率;QGn,i为第n场景节点i注入的无功功率;PPVi为节点i的总光伏接入容量;PDi为节点i的有功负荷;QDi为节点i的无功负荷;C(n,1)为C矩阵的第1列,表示第n场景光伏发电发出有功功率占其额定功率的百分比;C(n,2)为C矩阵的第2列,表示第n场景负荷占峰值负荷的百分比;Un,i为第n场景的节点i的电压幅值;Yij为节点导纳矩阵Y中第i行第j列的导纳值;θij为节点导纳矩阵Y中对应节点i,j之间的夹角;δni为第n场景的节点i的电压相位角;δnj为第n场景的节点j的电压相角。
3.3.2 变电站容量约束
(19)
(20)
式中:M1为母线i的有功功率容量上限值;M2为母线i的无功功率容量上限值;Ω为变电站母线集。
3.3.3 馈线容量限制
0≤In,ij≤Iijmax,∀i,j,n
(21)
2UniUnjcos(δnj-δni)]1/2,∀n,i,j
(22)
式中:Iijmax为节点i与节点j之间馈线电流容量限制;In,ij为第n场景节点i,j之间馈线电流。
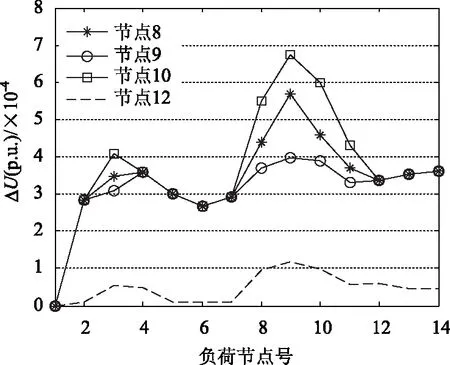
3.3.4 节点电压约束
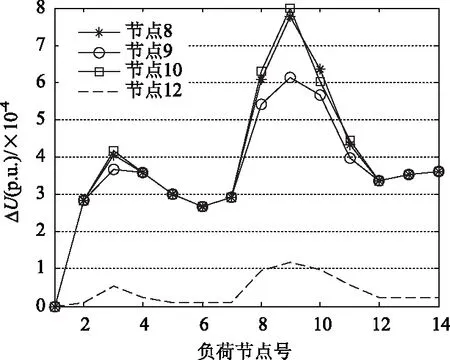
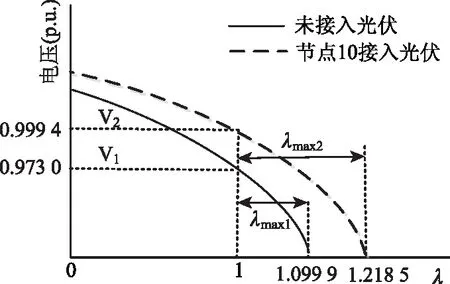
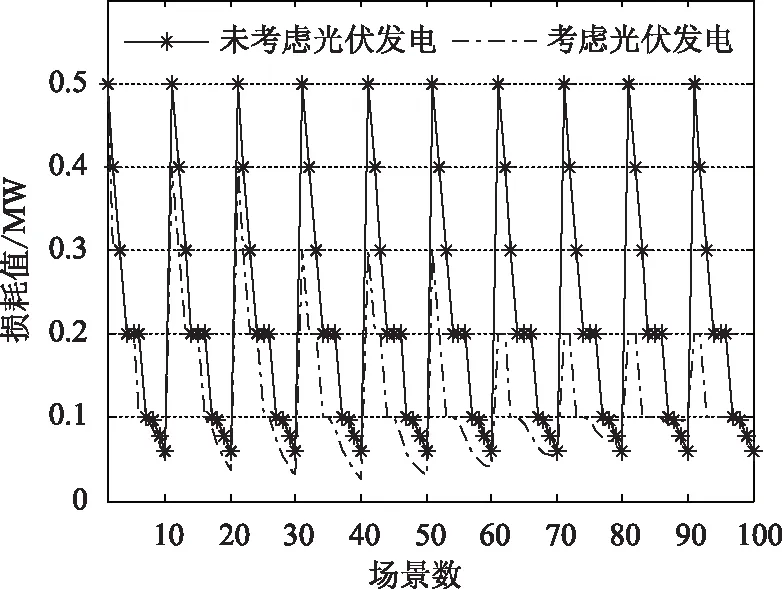
Ulo (23) 式中:Ulo为节点电压幅值下限值;Uup为节点电压幅值上限值。 3.3.5 节点最大渗透率限制 PPVi≤Pi,∀i∈B (24) 式中:Pi为节点i的最大渗透容量限制;B为候选节点集。 3.3.6 系统最大渗透率限制 (25) 式中:CFs为光伏的容量因子;y为最大渗透率限制即总峰值负荷的百分比。 以典型IEEE14配电网系统[19]进行测试。该系统的总峰值负荷为28.6MW。文中所选的光伏模块型号2150S,其参数为:额定功率150W,光电转换效率12%。整个配电网的电源供应由变电站(节点1)承担。分析过程中假设节点最大接入容量限制为10MW(约83 334块光伏模块),系统允许光伏模块最大渗透率为30%。 4.1 候选节点集的电压灵敏度分析 系统的稳定性可以根据灵敏度值的大小来判断。当电压灵敏度值大于零时,表示稳定运行。灵敏度值越小,系统就越稳定。相反,灵敏度值小于零时,表示系统不稳定,且负值数值越大越不稳定。电压灵敏度分析可以发现系统的电压支撑点。由图2和图3可知,对8、9、10、12节点注入相同容量的有功功率,它们的电压灵敏度都是大于零。根据图中曲线的位置可知,节点8、9、10的电压灵敏度值都比节点12的高,而且注入不同容量的有功功率,节点8、9、10的电压灵敏度变化很明显。相比之下,不论对节点12注入多大容量的有功功率,其电压灵敏度值变化不大,而且数值很小,这说明8、9、10节点是系统中起到电压支撑作用的节点。因此,将该节点作为候选节点集,接入光伏电源,判断光伏电源的接入位置和容量是否有利于系统稳定运行。 图2 电压灵敏度分析结果(渗透率10%) 图3 电压灵敏度分析结果(渗透率20%) 4.2 光伏发电的不同接入容量对电压分布影响 多场景光伏发电-负荷混合概率模型综合考虑100个场景,运用GAMS的DICOPT商业求解器[20]求解该模型。根据求解结果,最优接入光伏发电的节点为9、10节点,且总接入容量分别为3.4MW(约28 334光伏模块)和10MW(约83 334光伏模块)。为了分析在极端场景下光伏发电接入对配电网电压分布的影响,分别以列表2、3的7个场景为例,表中光伏接入容量即是占求解模型得出的总接入容量的百分比,通过牛顿-拉夫逊法潮流计算[21]来研究不同比例光伏接入容量对电压分布的影响。 表2 系统最小负荷情况 表3 系统最大负荷情况 根据图4和图5的曲线走势,光伏电源接入后, 3、8、9、10、11节点区域的电压分布有了明显改善。从配电网负荷分布可知, 光伏接入点属于重负荷区,光伏接入改善了重负荷区电压偏低的情况,并对电压的谷点有了明显的抬高。据4.1小节的电压灵敏度分析可知,节点9、 10的电压灵敏度高于其它节点,光伏接入后不仅提高了系统的稳定性,也改善了节点的电压分布。此外,从图中对应不同渗透率的曲线得知,随着光伏接入容量不断增大,对电压分布改善程度越明显。因此,通过分析接入点的光照强度分布情况,合理选择光伏模块的型号,可以保证光照强度充分利用,从而提高光伏发电的渗透率。 图4 系统最小负荷下光伏发电接入容量对电压分布影响 图5 系统最大负荷下光伏发电接入容量对电压分布影响 4.3 光伏发电对系统的电压稳定裕度的影响 算例分别采用3种负荷增长方式:方式A增加单个节点的负荷;方式B增加某一重负荷区域的负荷;方式C增加整个系统的负荷,具体情况如表4。通过这3种负荷增长方式来分析系统的电压稳定裕度大小情况。为了分析光伏发电接入点对电压稳定裕度的影响,需要对光伏的接入点进行分析。根据配电网负荷的分布情况,节点9、10为该系统重负荷节点,且该两节点的电压灵敏度相对较大,为系统的薄弱节点,若在该节点发生负荷扰动易于引起系统不稳定;节点2、6虽为配电网中负荷相对重的节点,但其灵敏度小。与节点9、10的稳定性相比,节点2、6会比较稳定。因此,根据表5的3种方案,运用连续潮流法[22]计算负荷功率的极限点,分析光伏发电接入对配电网电压稳定裕度的影响,并算出相应临界点处的有功功率和无功功率。 表4 节点的负荷增加方式情况 表5 光伏接入情况 表6中方案2与方案3的3种负荷增长方式所求出的电压稳定裕度值相比,对应两个方案的同一种负荷增长方式所得到的电压稳定裕度值相差很大,其值超过了一倍。由此可见,光伏接入对配电网的电压稳定裕度有明显的改善作用。方案1与方案2的电压稳定裕度相对比,由于9、10节点的电压灵敏度相对高,光伏接入该节点后,对电压稳定裕度的提高效果比接入2、6节点更好。 表6 IEEE14配电系统测试结果一览表 图6中x轴代表负荷裕度λ,从图中P-V曲线可以看出,未接入和接入光伏发电的电压稳定裕度区别很大。当光伏发电接入节点10,并注入8MW的有功功率(相当于30%总负荷的有功功率),电压由常规运行点V1(0.973 0)增加到V2(0.999 4),同时最大负荷裕度由λmax1增加到λmax2,说明了光伏发电的接入有助于改善节点的电压分布外,也大大提升了该节点的电压稳定裕度。 图6 光伏发电对电压稳定裕度的影响 4.4 分布式光伏发电对系统网损的影响 分布式光伏发电接入配电网可改变系统的潮流分布,从而影响系统网损。因此,在分布式光伏发电选址与定容的研究中,有必要考虑其对系统网损产生的影响。 图7 光伏发电接入对系统损耗的影响 图7展示了未考虑光伏发电和考虑光伏发电两种情况的系统网损。这是通过联立求解100个场景,最优接入光伏发电后对系统网损的影响。图中虚线表示未考虑光伏接入情况,实线表示考虑光伏发电接入情况。从整体上看,光伏接入配电网后,大大降低了系统损耗。根据图1的场景结构图可知,同样的负荷水平,不同的光伏接入容量,对系统的损耗产生不同的影响。随着光伏接入容量逐渐增大,对电压分布的改善作用明显增加,网络损耗也逐渐减少。但是,随着光伏接入容量达到最大时,光伏接入后的网络损耗比未接入光伏时高,如80、89、90和98~100处的网损情况。引起这种反差的主要原因是对应这6个场景的光伏出力状态PPV已达到最大值,而系统的负荷处于低谷水平,这会产生大量多余的功率逆流,使线路上的功率传输增大,损耗也随之增大。但从整体的曲线交错情况可知,光伏接入系统后,明显减少了系统的网损。 考虑到光伏发电出力的随机性和负荷的不确定性,本文建立了多场景光伏发电-负荷混合概率模型,以改进VPII指标为目标,在电网运行约束内,分析光伏的接入点和安装容量对配电网电压稳定裕度的影响。以典型IEEE14配电网系统为算例,计算结果表明,通过合理选择光伏的接入点和安装容量能够有效提高配电网的电压稳定裕度。同时,也改善了重负荷区域的电压分布,并验证了合理选择分布式光伏发电的接入点和容量可提升配电网的稳定性、降低系统的网损。此外,本文运用电压灵敏度分析选出灵敏度较高的节点,作为候选节点集,在候选节点集中考虑接入光伏发电,大大提高了选址分析效率,能够准确、快速确定光伏的接入点。 [1] Atwa Y M, El-Saadany E F. Optimal Allocation of ESS in Distribution Systems With a High Penetration of Wind Energy[J]. Power Systems, IEEE Transactions on, 2010,25(4):1815-1822. [2] Prada R B, Souza L J. Voltage stability and thermal limit: constraints on the maximum loading of electrical energy distribution feeders[J]. Generation, Transmission and Distribution, IEE Proceedings-, 1998,145(5):573-577. [3] Haiyan C,Jinfu C, et al. Power flow study and voltage stability analysis for distribution systems with distributed generation[C]// Power Engineering Society General Meeting, 2006. IEEE. 2006:1-8. [4] 张鑫,陈秋南,韦刚,等. 分布式电源分布特性对微电网电压质量的影响[J]. 现代电力, 2013,30(6):32-37. [5] 陈海焱, 段献忠, 陈金富. 计及配网静态电压稳定约束的分布式发电规划模型与算法[J]. 电网技术, 2006,30(21):11-14. [6] 雷金勇,甘德强.考虑配电网静态电压稳定性的用户自备分散电源准入功率计算[J]. 电网技术, 2010,34(3):162-168. [7] 迟永宁,刘燕华,王伟胜,等. 风电接入对电力系统的影响[J]. 电网技术, 2007,31(3):77-81. [8] 刘新东,郭容,张建芬,等.计及风力发电的配电网电压稳定性评估框架研究[J]. 电力系统保护与控制, 2013,41(17):77-81. [9] Van Geert, Edwin. Increased uncertainty a new challenge for power system planners[C]// IEE Colloquium(Digest), 1998,200, 1/1-1/6. [10]丛鹏伟,陈昕玥,唐巍,等. 基于机会约束规划含光伏发电的配电网故障恢复[J]. 电网技术, 2014,38(1):99-106. [11]J M S Pinheiro C R R D. Probing the new IEEE Reliability Test System (RTS-96)- HL-II assessment[J]. Power Systems, IEEE Transactions on, 1998, 13 (1): 171-176. [12]Singh C, Kim Y. An efficient technique for reliability analysis of power systems including time dependent sources[J]. Power Systems, IEEE Transactions on, 1988, 3(3):1090-1096. [13]陈敏,张步涵,段献忠,等.基于最小奇异值灵敏度的电压稳定薄弱节点研究[J]. 电网技术, 2006,30(24):36-39. [14]李斌,刘天琪,李兴源.分布式电源接入对系统电压稳定性的影响[J]. 电网技术, 2009,33(3):84-88. [15]王景亮,张焰,王承民,等. 基于灵敏度分析与最优潮流的电网无功/电压考核方法[J]. 电网技术, 2005,29(10):65-69. [16]Walling R A, Saint R, Dugan R C, et al. Summary of Distributed Resources Impact on Power Delivery Systems[J]. Power Delivery, IEEE Transactions on, 2008, 23(3):1636-1644. [17]Zeineldin H H, El-Saadany E F, Salama M M A. Distributed Generation Micro-Grid Operation: Control and Protection: Power Systems Conference: Advanced Metering[C]//Protection, Control, Communication, and Distributed Resources, 2006,105-111. [18]Chiradeja P, Ramakumar R. An approach to quantify the technical benefits of distributed generation[J]. Energy Conversion, IEEE Transactions on, 2004,19(4):764-773. [19]丁昊,万路路,王磊. 配电网电动汽车优化充电研究[J]. 华东电力, 2011,39(12):2049-2053. [20]魏传江,王浩,谢新民,等. GAMS用户指南[M]. 北京:中国水利水电出版社,2009. [21]陈珩.电力系统稳态分析[M].3版,北京:中国电力出版社,2007. [22]陈得治,张伯明,方兴.节点注入功率模式对电压稳定裕度的影响[J]. 电网技术, 2009,33(2):62-67. (责任编辑:杨秋霞) Locating and Sizing of Photovoltaic Power Generations by Considering Voltage Stability Margin of Distribution System BAI Xiaoqing, WU Xueying, LI Peijie, YANG Xiuju (Guangxi Key Laboratory of Power System Optimization and Energy Technology(Guangxi University),Nanning 530004,China) For the stochastic characteristics of the power output of photovoltaic generation and the volatility of load, a hybrid probability model of multiple scenarios photovoltaic power generation-load is proposed by considering the occurrence probabilistic of the load and photovoltaic power in different states. The supporting points of the system voltage are found by using voltage sensitivity analysis method, which are taken as the candidate buses of the photovoltaic installation to increase the efficiency of photovoltaic locating. Taking improved voltage profile improvement index (VPII) as an objective function, the locating and sizing models of photovoltaic power generation are built by adding the hybrid probability model of multiple-scenarios photovoltaic power generation-load into power flow equations. In the end, the rationality and effectiveness of the proposed model is verified by taking the IEEE14 radial distribution grid test system as calculation case. The simulation results show that the reasonable choice of locating and sizing of photovoltaic power generations can effectively improve the voltage stability margin of distribution system, increase the voltage stability, and reduce the loss. photovoltaic power generation; distribution system; improve voltage profile improvement index; hybrid probability model of photovoltaic power generation-load; the candidate buses; voltage stability 1007-2322(2015)04-0034-08 A TM715 国家自然科学基金项目(51367004);广西自然科学基金项目(2011GXNSFA018026) 2014-07-07 白晓清(1969—),女,博士,副教授,研究方向为电力系统最优化,E-mail:baixq@gxu.edu.cn; 吴雪颖(1987—),女,硕士研究生,研究方向为电力系统最优化, E-mail:wuxueying830@163.com; 李佩杰(1984—),男,博士,副教授,研究方向为最优化理论在电力系统小干扰稳定中的应用、电力系统稀疏、并行运算,E-mail:beyondpeijie@163.com。4 算例分析




5 结 论
