基于需求侧响应的微网孤网运行实时调度策略研究
2015-05-05杨明玉
杨明玉,韩 旭
(华北电力大学电气与电子工程学院,河北保定 071003)
基于需求侧响应的微网孤网运行实时调度策略研究
杨明玉,韩 旭
(华北电力大学电气与电子工程学院,河北保定 071003)
鉴于独立运行模式下,微网处于自给自足状态,内部会产生不平衡功率,为使供电更加经济可靠,提出了一套基于需求侧响应的实时调度策略。建立了计及负荷曲线平稳度和负荷转移成本双重指标的日前负荷转移规划模型,在需求侧转移部分可转移负荷平滑负荷曲线;微网运行期间,实施基于蓄电池三段式充放电的实时调度策略安排各可控型微源及蓄电池出力,有利于蓄电池保持足够的充放电裕量,进一步削减功率缺额及功率浪费。策略中建立负荷优化分配模型优化各可控型微源出力,减小微网运行成本。最后以一小型微网系统为例,通过与不计及蓄电池折旧成本的日前调度结果对比,证明在负荷转移平滑负荷曲线及实时调度策略的双重作用下,不平衡功率得以削减。
独立运行;负荷转移;三段式;实时调度;不平衡功率
0 引 言
随着全球能源和环境问题日益突出,太阳能,风能等可再生能源的应用已引起世界各国关注。分布式电源(DG)低污染,高效且可就近负载布置,但其大规模渗入也会对大电网带来一些负面影响,其不可控性会对电网稳定性造成冲击,而系统往往采取隔离,切机等方式,大大削弱其优势和潜能[2]。随着各国学者的深入研究,微网应运而生。
微网包含了各种分布式电源、负载、储能单元和控制装置,存在并网和孤网两种运行状态,并网时可与大电网交换能量,由大电网保证其内部功率平衡及电压、频率稳定,大电网故障时转入独立运行模式,在一些偏远地区也会有风光柴储小型微网独立供电。独立运行状态下微网仅靠内部电源和储能装置维持功率平衡,而可再生能源出力受光照、风速等环境因素影响,输出功率具有波动性,微网负荷预测不精确,都可能导致微网实时运行期间出现功率缺额及功率浪费两种不平衡功率。
目前国内外微网研究大多集中在微网控制,多目标经济运行及其算法,对削减不平衡功率的实时调度策略研究甚少。文献[3]提出了一种基于遗传算法的微网能量管理模型,通过能量平衡约束优化管理储能单元充放电,并建立了并网和孤网两种运行模式下发电成本最小经济调度数学模型安排各机组出力,但实际上是一种日前规划;文献[4]针对光伏发电、风力发电及负荷的不确定性,采取机会约束规划建立动态经济调度模型,但要保持较高可靠性水平会增大运行成本;文献[5]介绍了一种独立运行模式下计及可中断负荷的实时调度策略,通过储能单元区间划分及压缩可控型微源基点运行功率范围来确保有足够的功率调节裕量。
本文提出了一套基于需求侧响应的独立运行模式下实时调度策略。用户通过参与负荷转移项目转移部分可转移负荷,一定程度上平滑负荷曲线,可减少不平衡功率的出现,并通过建立日前负荷转移模型求解转移后各时段负荷;微网运行期间,鉴于可再生能源输出功率具有波动性,采取基于蓄电池三段式充放电的实时调度策略安排各可控型微源及蓄电池出力,使蓄电池保持足够的充放电裕量,进一步削减不平衡功率。
1 日前负荷转移规划模型
微网一天内存在用电高峰和低谷时段,平滑负荷曲线可缩小峰谷负荷差,一定程度上减少不平衡功率的出现。提出了负荷曲线平稳度和负荷转移成本两种指标,将一天划分为24时段,建立了计及负荷曲线最小波动及负荷转移成本最小双重目标下的日前负荷转移模型,并通过遗传算法求解各时段负荷转移功率。本文假定可转移负荷持续时间均为一小时。
1.1 负荷曲线平稳度指标
指标LCS(Load Curve Smoothness)旨在衡量负荷曲线平稳程度,表达式为
(1)
(2)
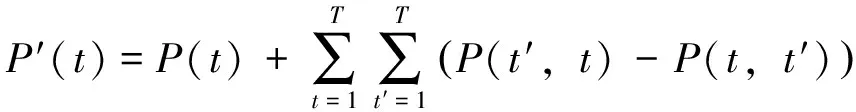
(3)
式中:P′(t)为负荷转移后t时段负荷;P(t)为负荷转移前t时段负荷;Pav为一天内平均负荷;P(t,t′)为时段t向时段t′转移的负荷量;P(t′,t)为时段t′向时段t转移的负荷量;T为调度时段总数,根据表达式,显然该指标越小越好。
1.2 负荷转移成本指标
指标LTC(Load Transfer Cost)旨在尽量减少转移负荷时需补偿用户带来的成本,表达式为
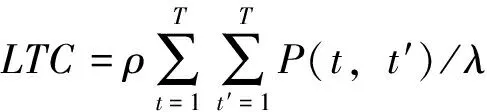
(4)
ρ=φ|t-t′|
(5)
式中:ρ为转移单位负荷所需补偿费用,与负荷转移时段跨度|t-t′|有关;φ为固定费用部分。为将该指标量纲化为一,与负荷曲线平稳度指标量纲统一,引入参数λ,单位为元,同时,该参数也是目标函数中分配两大指标权重的重要参数,λ大则负荷转移成本指标权重较小,反之较大。
1.3 目标函数
基于两种指标的目标函数为
(6)
目标函数中两个指标量纲均统一为一,则多目标函数转化为单目标函数,参数λ可同时作为两指标的权重参数。
1.4 约束条件
本文将微网负荷划分为可转移负荷和不可转移负荷两部分,并计及各时段最大转出可转移负荷功率及最大接纳可转移负荷功率约束。

(7)
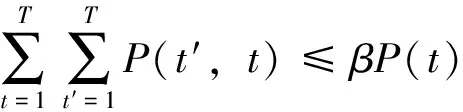
(8)
式(7)为t时段最大转出可转移负荷功率约束,P(t)为负荷转移前t时段负荷,因子α设定原则为白天较小,晚上较大,负荷峰时段较大,平时段较小,深夜人都在休息,一般不会有负荷转入与转出,α为0;式(8)为t时段最大接纳可转移负荷功率约束,因子β设定原则为白天较大,晚上较小,负荷峰时段较小,平时段较大,深夜为0。
1.5 遗传算法求解流程
本文采用遗传算法求解负荷转移规划模型最优解,具体步骤如下:
① 输入模型中参数φ、λ、α、β值;
② 算法初始化,包括种群规模N,交叉概率Pc,变异概率Pm,最大迭代次数,确定算法终止条件;
③ 种群初始化,随机生成N个个体,这里采用浮点数编码方式,无需编码,每个个体由各时段向其它时段转移的负荷功率组成,即染色体基因为各时段转移负荷功率,考虑到α、β因子的设定,有些转移负荷功率直接置0,并评估个体适应度;
④ 根据个体适应度对种群个体进行选择,交叉、变异、生成子代种群;
⑤ 判断是否满足终止条件,不满足返回步骤④,满足则输出结果。
2 蓄电池三段式充放电原理
2.1 净负荷、不平衡功率及蓄电池SOC
净负荷定义为Pnet=Pload-Ppv-Pw,其中Pload为微网负荷,Ppv为光伏出力,Pw为风电出力。
不平衡功ΔP包括功率缺额及功率浪费,各可控型微源和蓄电池皆最大出力仍不能满足净负荷时则出现功率缺额,净负荷小于零或各机组最小出力超出负荷需求,且蓄电池充电空间不足时则出现功率浪费,ΔP缺额、ΔP浪费公式见图1。
实时调度策略中需判断蓄电池荷电状态SOC[9],定义为蓄电池剩余容量与总容量比值[11]:
(9)
式中:Cbat为蓄电池组的安时容量,单位为Ah;I为蓄电池在调度周期内放电电流,单位A。为保证蓄电池有足够充放电裕量,设置了蓄电池3种荷电状态SOCmin、SOCmid、SOCmax,将蓄电池SOC划分为4区间。
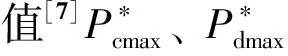
(10)
(11)
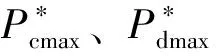
Icmax=Idmax=0.2×Cbat/Δt
(12)
2.3 蓄电池三段式充放电原理
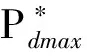
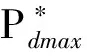
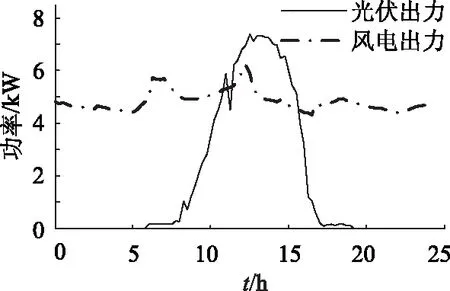
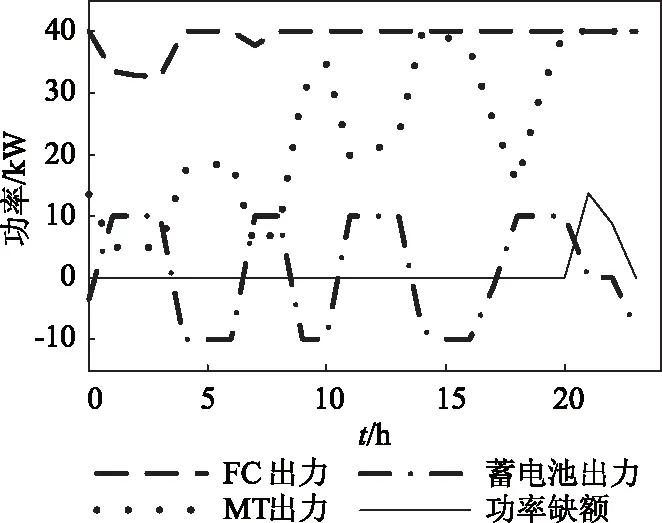
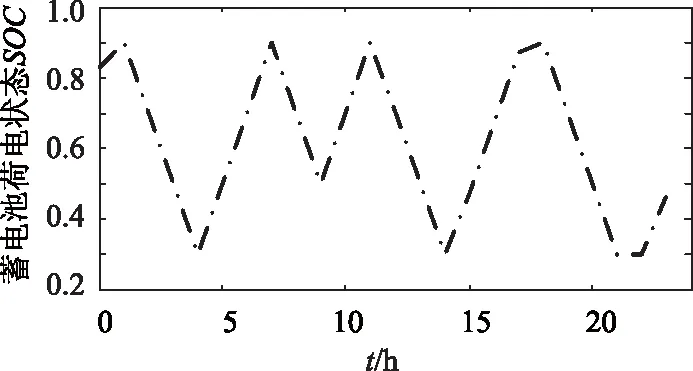
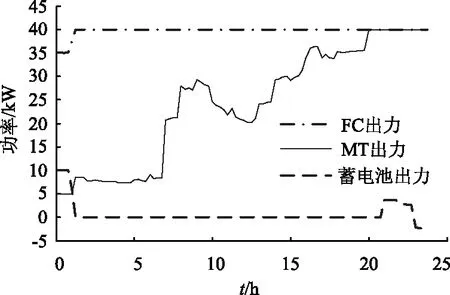
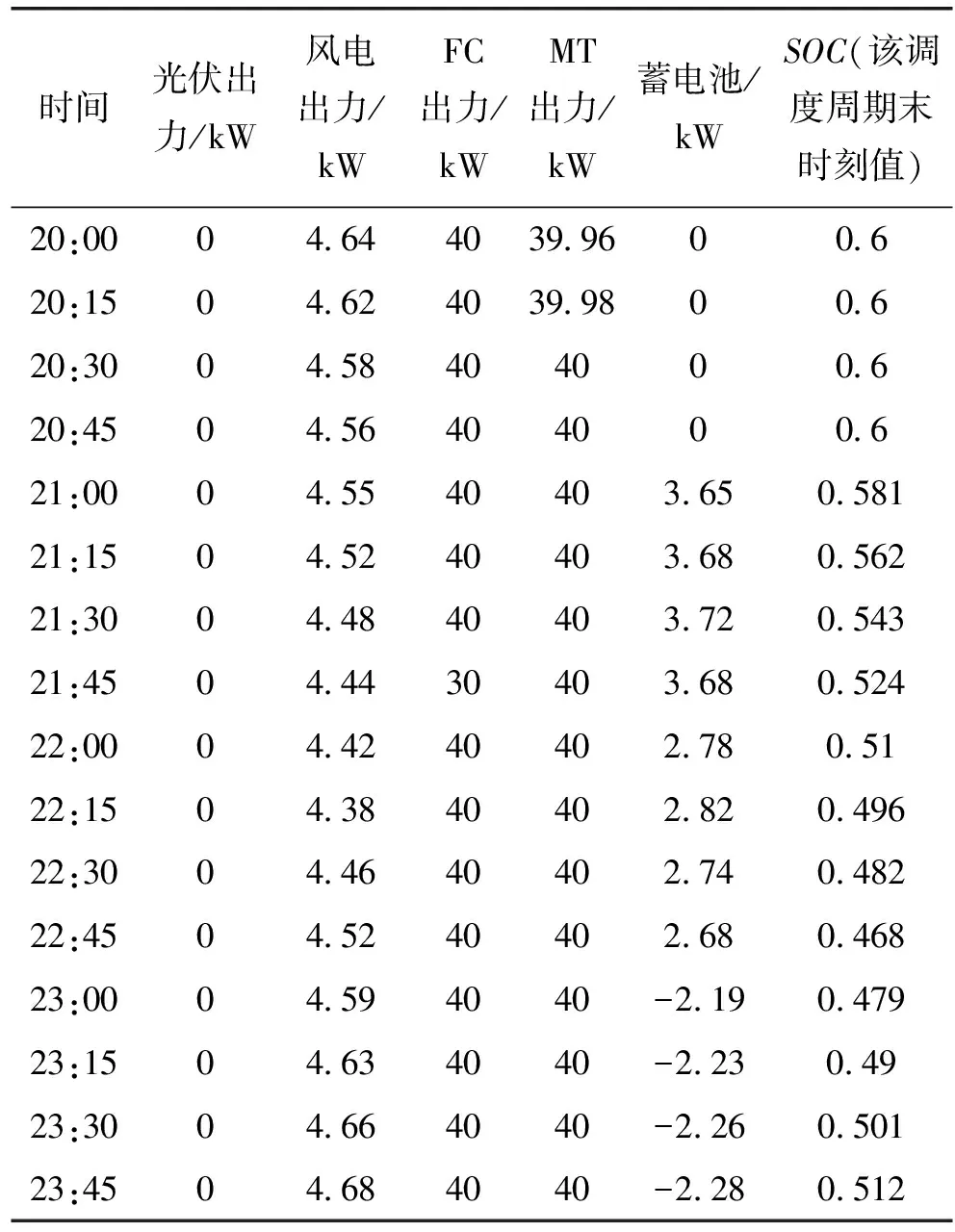
SOC 三段式充放电有利于蓄电池保持充足的充放电裕量,吸收不平衡功率。 实时运行期间,为确保蓄电池有足够充放电裕量,进一步削减不平衡功率,采取基于蓄电池三段式充放电的实时调度策略安排各可控型微源及储能装置出力,实时调度策略流程如图1。 3.1 策略图中蓄电池最大可充电功率Pcmax[7],最大可放电功率Pdmax1、Pdmax2 Pcmax=min[(SOCmax-SOC)Cbat× (13) Pdmax1=min[(SOC-SOCmid)Cbat× (14) Pdmax2=min[(SOC-SOCmin)Cbat× (15) 图1 独立运行模式下实时调度策略流程图 3.2 策略图A部分 蓄电池荷电状态处于[SOCmin,SOCmid],此时可控型微源有余力对蓄电池实时充电,保证蓄电池有放电裕量,并将充电功率和净负荷一起作为负荷,充电功率为 Pc=min[(SOCmid-SOC)CbatUbat/(Δtηc), (16) 由公式可知,当荷电状态等于SOCmid时充电功率为零,总负荷为Pc+Pnet。 3.3 策略图B部分 蓄电池荷电状态大于SOCmid,当蓄电池放电Pdmax1,可控型微源最小出力时不能满足净负荷时,则将净负荷优化分配给各可控型微源。 3.4 策略图C部分 此时蓄电池荷电状态小于SOCmin,且各可控型微源有余力,需对蓄电池充电使其荷电状态恢复到允许区间内,充电功率为 Pc=min[(SOCmin-SOC)CbatUbat/(Δtηc), (17) 为减小微网运行成本,策略中A、B、C部分涉及负荷优化分配模型。 4.1 目标函数 式中:wCaF2为试样中氟化钙的含量,%;1.9481为全钙含量换算成氟化钙含量的系数;0.7801为碳酸钙含量换算成氟化钙含量的系数。 以微网运行成本最小的目标函数为 (18) Cf(PGi)=F(PGi)PGiΔt (19) COM(PGi)=KOMiPGiΔt (20) 式中:C为一个实时调度周期内微网运行总成本;Cf(PGi)为一个实时调度周期内各可控型微电源能耗成本;COM(PGi)为一个实时调度周期内各可控型微电源运行维护成本;PGi为一个实时调度周期内各可控型微电源有功出力;n为可控型微电源总数;KOMi为各可控型微电源运行维护系数;F(PGi)为各可控型微电源单位电量成本;Δt为实时调度周期。 4.2 约束条件 ① 功率平衡约束 (21) 式中:Pbat为正时蓄电池放电;Pbat为负时蓄电池充电,策略中已给出不同情况蓄电池充放电Pbat值。 ② 可控型微电源出力约束 PGimin≤PGi≤PGimax (22) ③ 可控型微源爬坡约束[7] P(t)-P(t-1)≤Rup (23) P(t-1)-P(t)≤Rdown (24) 式中:Rup为上升功率约束;Rdown为下降功率约束。 4.3 遗传算法 求解流程与1.5类似,在这里指出遗传算法中个体仅由某调度周期可控型微源输出功率组成。 5.1 算例系统 本文算例选取一小型微网系统,包含薄膜固定式光伏发电、风力发电、微型燃气轮机,燃料电池以及储能蓄电池。其中光伏发电额定功率为10kW,风力发电额定功率为10kW。蓄电池充放电效率均为1,SOCmax=0.9,SOCmid=0.6,SOCmin=0.3,初始荷电状态为0.83;微燃机和燃料电池参数如表1。微型燃气轮机及燃料电池成本计算公式以及ηe(t)与Pe(t)之间函数关系式遵循文献[11]。光伏电池和风力发电机均工作在最大功率点跟踪模式,输出功率遵循典型曲线如图2,微网负荷遵循典型双峰型负荷曲线如图3。 表1 可控型微源参数 图2 光伏风电出力 图3 转移前后负荷曲线 5.2 不计及蓄电池折旧成本日前调度结果分析 将一天划分为24时段,目标函数如下: C缺额ΔP缺额Δt-C浪费ΔP浪费Δt (25) 为了观察各时段不平衡功率值,嵌入变量ΔP缺额、ΔP浪费,C缺额、C浪费为虚拟费用,C缺额在所有成本中取值最大,C浪费取极小值,确保微网内部没有出现不平衡功率时,ΔP缺额、ΔP浪费值为0,同时C缺额最大,可减少功率缺额出现。其余与优化分配模型含义一致。约束条件涉及功率平衡约束,可控性微源出力约束,爬坡约束,蓄电池最大充放电约束,和蓄电池SOC约束,在其他文献均有介绍,本文不再详述。SOCmin=0.3,SOCmax=0.9,功率平衡约束更改为 (26) 式中:ΔP缺额理解为内部出现功率缺额时电源需多发功率;ΔP浪费理解为内部出现功率浪费时电源需少发功率。一天内各时段MT、FC、蓄电池出力及ΔP缺额、ΔP浪费情况如图4,蓄电池SOC变化如图5。 图4 各时段FC,MT,蓄电池出力及功率缺额 图5 一天内蓄电池SOC变化 遗传算法中个体由各时段可控型微源输出功率、蓄电池出力、功率缺额及功率浪费组成,蓄电池充放电成本相当于0。 图4可以看出,目标函数中C缺额虽为最大,可一定程度上避免功率缺额出现,白天高峰期没有出现功率缺额,但晚上用电高峰期21点和22点两时段分别出现功率缺额,算例中可再生能源额定功率较小,负荷相对较重,未造成功率浪费现象。由图5观察到,由于不计蓄电池折旧成本,蓄电池荷电状态一天内时起时落,不能保证在大多时段有充放电裕量吸收不平衡功率。由此可见一般日前调度模型应用于微网独立运行有局限性。 5.3 日前负荷转移规划分析 根据日前负荷转移规划模型,得出负荷平移后一天内负荷曲线如图3,并给出各时段负荷转移情况如表3。假定可转移负荷持续时间均为一小时,固定费用φ为0.1元/kW,参数λ设置为95元,因子α、β的设定如表2。 表2 各时段因子α、β值 表3 各时段负荷转移情况 如图3所示,较之转移前负荷曲线,新的负荷曲线较为平稳,由于深夜因子α、β设定为0,没有负荷转移,0点至6点负荷曲线与原曲线重合;从表3可以看出,可转移负荷大多从双峰时段就近转移,以节省成本,达到了在负荷侧削减高峰时段负荷,平滑负荷曲线的目的。最终负荷曲线平稳度指标LCS值为0.741 5,负荷转移成本指标LTC值为0.203 2。 5.4 实时调度策略分析 图6 各实时调度周期FC、MT和蓄电池出力 假定各时段负荷在该时段保持不变,且负荷转移得以实施,微网实时运行期间采取有效调度策略安排各可控型微源及蓄电池出力,根据所提出实时调度策略使用matlab软件编程,得一天内MT,FC和蓄电池在各个调度周期内出力如图6,各调度周期功率缺额为0,故并未在图中体现,实时调度周期为15min,同时给出蓄电池荷电状态SOC一天内变化,如图7所示。 图7 蓄电池SOC一天内变化 时间光伏出力/kW风电出力/kWFC出力/kWMT出力/kW蓄电池/kWSOC(该调度周期末时刻值)20:0004 644039 9600 620:1504 624039 9800 620:3004 58404000 620:4504 56404000 621:0004 5540403 650 58121:1504 5240403 680 56221:3004 4840403 720 54321:4504 4430403 680 52422:0004 4240402 780 5122:1504 3840402 820 49622:3004 4640402 740 48222:4504 5240402 680 46823:0004 594040-2 190 47923:1504 634040-2 230 4923:3004 664040-2 260 50123:4504 684040-2 280 512 由图6可以看出,由于燃料电池电价较低,一直处于满发状态,随着负荷增大,微燃机出力逐渐增加,在负荷高峰时段各可控型微源皆最大出力仍不能满足净负荷时,蓄电池放电填补高峰期功率缺额,图7给出了一天内蓄电池荷电状态变化,由于可转移负荷从高峰时段就近转移,平滑了负荷曲线,蓄电池在初始阶段放电至荷电状态为0.6后基本不变,只在晚上用电高峰期可控型微源功率不足时放电,荷电状态下降后由于各可控型微源出力对其实时充电,荷电状态得以恢复至SOCmid左右,可见本文所提出的三段式充放电原理有利于蓄电池保持足够的充放电裕量削减不平衡功率。 表4给出了晚上用电高峰期的实时调度情况,蓄电池SOC最低下降至0.468。各调度周期负荷均得以满足,证明了负荷转移平滑负荷曲线及实时调度策略的双重作用,很好地控制了功率缺额的出现。本算例可再生能源额定功率较小,负荷相对较重,未造成功率浪费现象,若其额定功率增大,根据实时调度策略,蓄电池荷电状态基本处于SOCmid左右,有裕量吸收可再生能源发出的多余功率,减少功率浪费。 独立运行模式下,鉴于可再生能源输出功率具有波动性,微网负荷预测不精确,导致内部出现不平衡功率,为使供电更加经济可靠,本文提出了一套基于需求侧响应的实时调度策略。建立了计及负荷曲线平稳度和负荷转移成本双重指标的日前负荷转移规划模型,在需求侧转移部分可转移负荷平滑负荷曲线;微网运行期间,实施基于蓄电池三段式充放电的实时调度策略安排各可控型微源及蓄电池出力,有利于蓄电池保持足够的充放电裕量,削减不平衡功率。策略中建立负荷优化分配模型优化各微源出力,减小微网运行成本。最后通过一小型微网系统验证策略有效性。 [1] CHIRADEJA P. Benefit of Distributed Generation: A Line Loss Reduction Analysis[J]. IEEE Transmission and Distribution Conference & Exhibition, Asia and Pacific Dalian, China, 2005. [2] 黄伟,孙昶辉,吴子平,等.含分布式发电系统的微网技术研究综述[J]. 电网技术,2009,33(9):14-18. [3] 陈昌松,段善旭, 等.基于改进遗传算法的微网能量管理模型[J]. 电工技术学报, 2013, 28(4):196-201. [4] 徐立中. 微网能量优化管理若干问题研究[D]. 杭州:浙江大学,2011. [5] 石庆均,江全元. 包含蓄电池储能的微网实时能量优化调度[J]. 电力自动化设备,2013,33(5):76-82. [6] 丁明,张颖媛,茆美琴,等. 包含钠硫电池储能的微网系统经济运行优化[J]. 中国电机工程学报,2011,31(4):7-14. [7] 石庆均. 微网容量优化配置与能量优化管理研究[D].杭州:浙江大学,2012. [8] Richard Lau, Sami Ayyorgun. Strategy and Modeling for Building DR Optimization[J]. IEEE SmartGridComm.2011. [9] PILLER SPERRIN MJOSSEN A. Methods for state of charge determination and their applications[J]. Power Sources,2001,96(1):113-120. [10]牛铭,黄伟,郭佳欢,苏玲. 微网并网时的经济运行研究[J]. 电网技术,2010,34(11):38-42. [11]陈洁,杨秀,朱兰,张美霞. 基于遗传算法的热电联产型微网经济运行优化[J]. 电力系统保护与控制,2013,41 (8):7-15. [12]吴雄,王秀丽,崔强. 考虑需求侧管理的微网经济优化运行[J]. 西安交通大学学报,2013,47(6):90-96. [13]王成山,洪博文,等, 不同场景下的光蓄微电网调度策略[J].电网技术,2013,37(7):1776-1782. (责任编辑:林海文) Reseach on Real-time Scheduling Strategy for Micro-grid Operation in IslandMode Based on the Demand Side Response YANG Mingyu,HAN Xu (School of Electrical and Electronic Engineering,North China Electric Power University,Baoding 071003, China) Due to micro-grid supplies electricity by itself in island mode, the unbalanced power will be produced. In order to make power supply more economical and reliable, a real-time scheduling strategy based on the demand side response is put forward in this paper. Day-ahead load transfer model, which considers such indexes as load curve smoothness and load transfer cost, is built to smooth the load curve by transferable load at demand-side transfer part. During the operation of micro-grid, the real-time scheduling strategy based on battery three-step charging and discharging is implemented to arrange each controllable micro-source and battery output, which can maintain enough battery charging and discharging margin and cut down the power shortage and power waste. Moreover, the optimal load distribution model is proposed in the dispatch scheme to optimize the output of the controllable micro-source, reduce the micro-grid operation cost. In the end, taking a small micro-grid system as an example, by comparing with the day-ahead planning results without considering the battery depreciation cost, it is shown that the unbalanced power can be reduced under both functions of load curves smoothening by load transfer and the real-time scheduling strategy. operation in island mode; load transfer; three-step; real-time schedule; the unbalanced power 1007-2322(2015)04-0012-07 A TM73 中央高校基本科研业务费专项资金资助(2014MS138) 2014-08-18 杨明玉(1965—),女,副教授,研究方向为电力系统继电保护,E-mail:yangmy1026@hotmail.com; 韩 旭(1988—),男,硕士研究生,研究方向为微电网能量调度, E-mail:lanyeyouming7@126.com。3 独立运行模式下实时调度策略
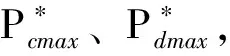


4 负荷优化分配模型
5 算例分析






6 结束语
