基于改进PHD粒子滤波的多目标检测前跟踪算法*

秦占师，张智军，陈稳，马赢

(空军工程大学 航空航天工程学院，陕西 西安 710038)

基于改进PHD粒子滤波的多目标检测前跟踪算法*

秦占师，张智军，陈稳，马赢

(空军工程大学 航空航天工程学院，陕西 西安 710038)

针对PHD-TBD算法存在目标数目估计不准，以及对交叉目标状态估计误差较大的缺点，提出了PHD-TBD的改进算法，通过推导更准确的PHD-TBD算法粒子权重更新表达式，实现对目标数目的准确估计；同时利用高斯混合模型(Gaussian mixture models，GMM)拟合PHD-TBD中重采样后的粒子分布，通过期望最大化算法(expectation maximum，EM)估计混合模型的参数，即可提取目标的状态。通过仿真实验表明，改进算法能够更准确地估计目标的数目和状态。

概率假设密度；粒子滤波；高斯混合模型；检测前跟踪；多目标

0 引言

检测前跟踪(track-before-detect，TBD)是低信噪比条件下对目标进行检测跟踪的有效方法[1]，它使用传感器的原始数据，对假设路径包含的点作几乎没有信息损失的相关处理，经过多帧积累来提升信噪比。目前，TBD技术广泛用于雷达、红外弱小目标的检测跟踪领域。

对于多目标TBD，不但需要解决单目标TBD中的高度非线性等问题，还需要解决多目标跟踪中的数据关联问题[2]，目前常用的方法有粒子滤波算法、动态规划算法、广义似然比算法、概率假设密度滤波算法[3-6]等。概率假设密度(probability hypothesis density，PHD)滤波是Mahler于2003年提出的，其中PHD是多目标后验概率密度的一阶统计矩，递推地传递目标状态的分布信息，不需要复杂的数据关联就能提取多目标的个数和状态。目前PHD滤波器的实现方式主要有粒子滤波实现[7](sequential Monte Carlo PHD，SMC-PHD)和高斯混合实现[8](Gaussian mixture，GM-PHD)。近年来，PHD已成为国内外学者的一个研究热点。

PHD滤波在检测前跟踪领域的应用才刚刚起步，有许多值得研究的问题。在文献[9]中，K. Punithakumar首次将概率假设密度滤波引入到多目标检测前跟踪中，实现了对目标数目和状态的估计。文献[2]对多目标观测模型进行了改进，并对噪声进行“泊松化”，使得PHD滤波器更好的应用于TBD算法中。文献[10]将平滑器引入到概率假设密度滤波中，克服了噪声的影响，提高了检测跟踪性能。

文章在研究已有PHD-TBD算法的基础上，针对目标数目估计不准，及对交叉目标状态估计误差较大的缺点，从标准的PHD滤波的粒子权重更新表达式出发，结合弱小点目标的似然函数，推导出更合理的粒子权重更新表达式。同时利用高斯混合模型拟合重采样后的粒子分布，通过期望最大化算法估计混合模型的参数，进而得到目标的状态。仿真实验验证了本算法的准确性和有效性。

1 多目标状态模型

1.1 目标运动模型

目标运动模型是指目标运动状态的帧间转移模型。为简化描述，假设目标为点目标，则k时刻多目标的运动状态定义为

(1)

式中：xk为k时刻单目标的状态向量，可以表示为

xk=Fxk-1+wk-1，

(2)

时刻目标的个数用Ek来表示，Ek是未知且时变的，可以表示为

Ek=Ek-1+ΔEk.

(3)

本文暂只考虑ΔEk={-1,0,1}的情况，即从k-1到k时刻，目标数目可以保持不变、增加一个或消亡一个。ΔEk的概率可表示为

Pr(ΔEk=-1)=Pdeath；Pr(ΔEk=1)=Pbirth；

Pr(ΔEk=0)=1-Pdeath-Pbirth.

1.2 多目标测量模型

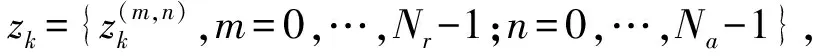
(4)

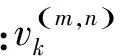
(5)

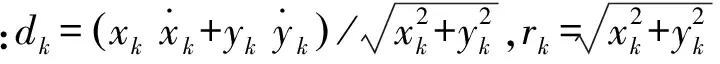
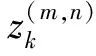
(6)

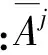
(7)

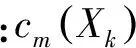
(8)

2 传统PHD-TBD算法

根据文献[2]，可以得到PHD滤波器的预测和更新公式为

(9)

(10)

式中：D(x)为多目标后验概率密度的PHD；ek(xk-1)为k-1时刻状态为xk-1的目标在第k时刻仍然存活的概率；γk(xk)为k时刻新生目标的随机有限集的PHD；bk(xk|xk-1)表示k-1时刻状态为xk-1的目标在k时刻衍生出状态为xk的目标随机有限集的PHD；κk(zk)为虚警集合的PHD；fk(xk|xk-1)为k-1时刻到k时刻的单目标马尔可夫转移概率。

由于基于粒子滤波的PHD算法可以适用于非线性非高斯噪声环境，因此文章采用粒子滤波来实现PHD-TBD算法。

基于粒子滤波PHD-TBD算法的基本思想是利用一组带有相应权值的粒子逼近PHD分布，通过预测和更新粒子来代替传递整个目标状态的后验概率密度分布，在获得PHD后，对它在给定测量区域内进行积分，则可得到目标的数目，利用K-means等算法可以提取目标的状态。

传统算法的粒子权重更新公式考虑了所有的量测，不仅增大了计算量，还会导致目标数目估计不准确；目标状态提取通常采用K-means算法，当目标临近飞行及交叉飞行时，K-means算法对目标的状态估计误差很大。针对以上问题，本文作了相应的改进。

3 改进PHD-TBD粒子滤波算法

3.1 PHD滤波粒子权重更新表达式推导

对于任意粒子，标准PHD滤波的权重更新如式(11)和式(12)所示：

(11)

(12)

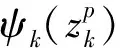
(13)

(14)

式中：

(15)

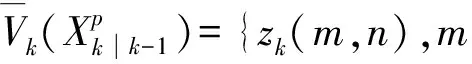
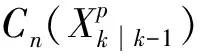
(16)

(17)

因此更准确的粒子权重更新表达式为

(18)

(19)

3.2 利用GMM提取目标状态

对于交叉飞行的目标，由于目标的量测存在重叠，以及传感器分辨率不足、杂波和噪声等因素的影响，使得重采样后的粒子分布变得更加复杂。它往往呈现复杂的多峰分布，相应目标的状态提取的难度也显著增加。传统PHD滤波器常采用K-means算法来提取目标状态，但是K-means算法属于“硬聚类”方法，它只能将数据中的一个元素分配给一个类别。这时如果仍采用K-means算法，多目标状态的提取效果将严重变差。相反，GMM属于“软聚类”方法，它可以根据一定的概率将数据中的一个元素分配给多个类别，故它尤其适用于聚类有重叠边界的数据。因此，文章采用GMM提取多目标的状态。

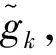
(20)

(21)

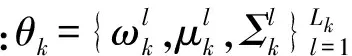
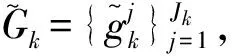
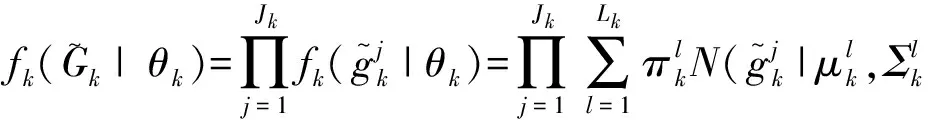
(22)

对参数集θk的估计方法有：极大似然估计、马尔可夫链蒙特卡罗方法(MCMC)、期望最大化估计(EM)；本文采用期望最大化估计方法，具体步骤参考文献[11]。

最终，在得到混合模型的参数估计θk后，可以求得时刻k的多目标状态：

(23)

3.3 改进PHD-TBD算法步骤

综合上述改进策略，改进PHD-TBD算法的具体步骤如下所示：

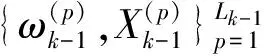
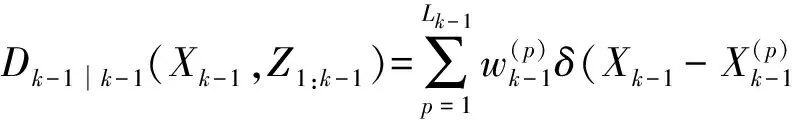
(1) 预测

预测的粒子通过以下方式产生：

(25)

式中：qk(·|Xk-1,Zk)为先验分布密度；pk(Xk|Zk)为新生目标的概率密度函数。

预测集合的PHD为

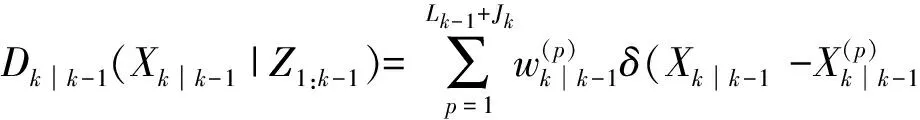
(26)

(27)

(2) 更新

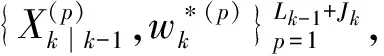
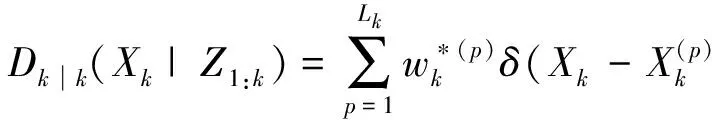
(28)

(3) 重采样

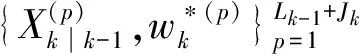
(29)

(4) 状态提取

4 仿真实验

4.1 仿真场景

仿真场景及参数设置：假设雷达观测区域为[0,5 000]×[0,5 000]，随机分布的杂波落入观测区域内的数量服从泊松分布；量测数据仅提供目标在二维直角平面空间上的信息；采样周期T=1 s，实验仿真时间为50 s，在观测区域内有3个目标在不同的时刻出现、消失，目标1和目标2在第10 s发生交叉。过程噪声标准差σW=15 m，观测噪声标准差σV=150 m，新生目标概率Pbirth=0.1，死亡目标概率Pdeath=0.1，杂波密度c(z)=15/km2，粒子数N=500， Monte Carlo仿真次数为1 000次。

4.2 仿真结果分析

假设目标交叉飞行，其初始飞行状态如表1所示。

表1 目标的初始位置和速度Table 1 Initial positions and speed of the targets

目标的真实飞行轨迹如图1所示。

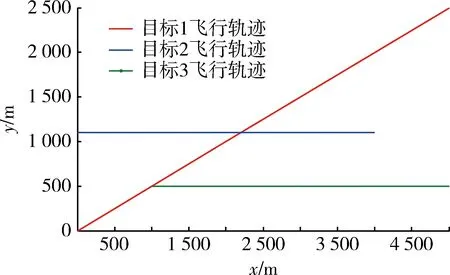
图1 目标真实飞行轨迹Fig.1 True trajectories of the target

由图1可以看出，初始时刻只有目标1和目标2，在第10帧，由目标1衍生出目标3，在第40帧，目标2消失在监控区域内，并且目标1和目标2在第22帧存在交叉，因此给后续的多目标状态提取带来了困难。

图2为多目标个数估计随时间变化曲线，由图2可以看出，2种算法都可以快速实时地检测到目标，对目标个数的估计都存在误差，但是由于杂波和目标交叉飞行的影响，传统算法的估计误差较大，而改进算法采用了更准确的粒子权重更新解析式，受杂波等因素的影响较小，多目标估计曲线的波动幅度相对较小。因此，改进算法对目标数目的估计精度更高。

图2 目标个数估计随时间变化曲线Fig.2 Target number estimates versus time

为了进一步比较2种算法的多目标估计稳定性，图3为2种算法的多目标个数估计的标准差(standard deviations，STD)随时间变化曲线。

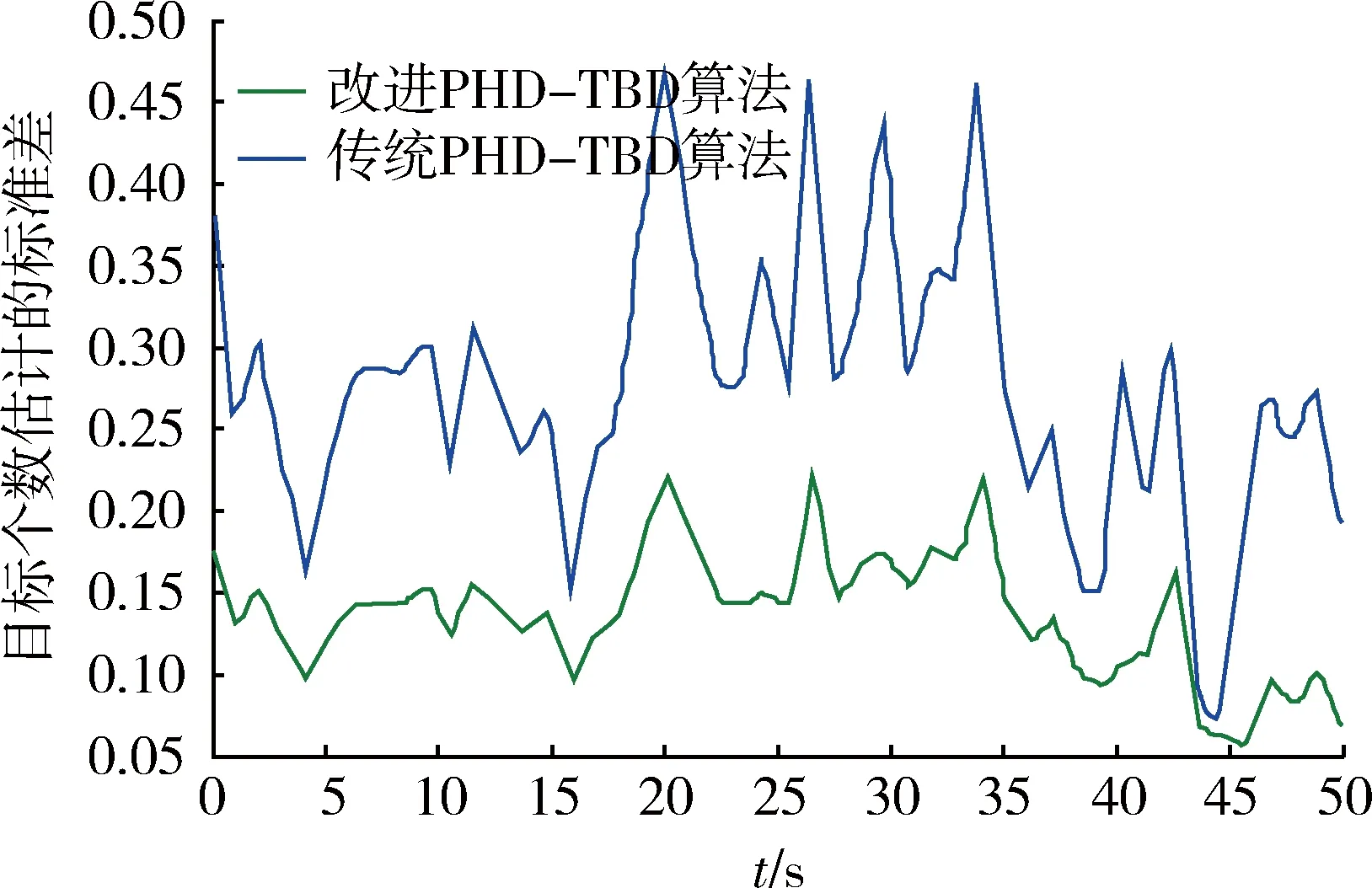
图3 目标个数估计的标准差随时间变化曲线Fig.3 Standard deviations of target number estimates versus time

由图3可以看出，2条曲线都会随时间波动，但传统算法对应曲线的波动幅度和标准差较大， 进而说明改进算法对目标个数的估计更加稳定。

由于基于PHD滤波器的多目标检测跟踪算法没有进行数据关联，因此通常的均方根误差(root mean square error，RMSE)不能用于评价PHD滤波的性能。在现有的文献中，大多采用Wasserstein距离(Wasserstein distance， WD)对此类算法的性能进行定量分析。WD的表达式[12]为

(30)

图4为2种算法状态估计的平均WD随时间变化曲线。由图4可知，两种算法对状态的估计都存在一定的误差，这是由于杂波以及目标的交叉飞行引起状态空间中的PHD出现错误峰值。相比传统算法，改进算法的WD较小，这是由于改进算法采用GMM方法提取目标状态，充分考虑了PHD本身的属性，将重叠的量测按照一定的概率分配给不同的目标，大大降低了上述因素的影响，因此，改进算法具有更高的状态估计精度。

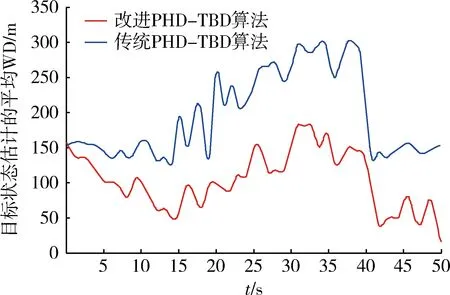
图4 目标状态估计的平均Wasserstein距离Fig.4 Averaged Wasserstein distance of target states estimates

为了比较2种算法的整体性能，本文在相同仿真实验条件下，得到两者的目标个数估计标准差、Wasserstein 距离和平均运行时间，并将上述性能指标列于表2。

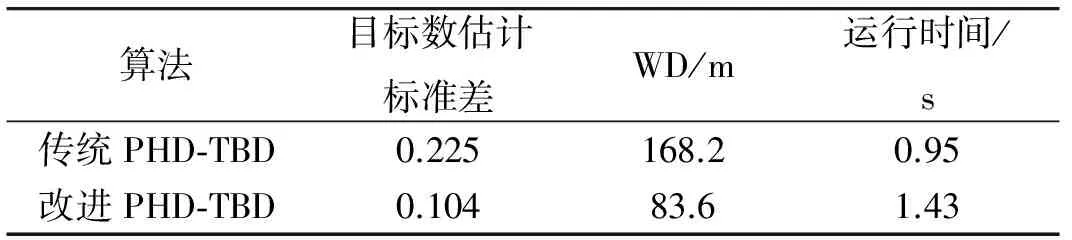
表2 2种算法的时间平均性能比较Table 2 Time averaged performance comparison for two algorithms

通过表2可以看到，在相同的仿真条件下，改进PHD-TBD算法的整体性能优于传统PHD-TBD算法，但改进算法需要耗费更多的时间，这也是本文后续工作所要解决的问题。

5 结束语

本文针对杂波环境下多目标数目估计不准，交叉目标状态估计误差较大的问题，提出了一种基于PHD粒子滤波的检测前跟踪算法。该算法从标准的PHD滤波粒子权重更新表达式出发，推导出更合理的PHD粒子权重更新解析式，从而实现了对目标数目的准确估计；在此基础上，利用GMM拟合重采样后的粒子分布，通过EM算法求得混合模型的参数，进而得到目标的状态，通过Matlab仿真实验表明，该方法能有效实现对雷达弱小多目标的检测跟踪，且性能优于传统算法。

[1] LONG Yun-li, XU Hui, AN Wei. Track-Before-Detect for Infrared Maneuvering Dim Multi-target via MM-PHD[J]. Chinese Journal of Aeronautics, 2012,25(2):252-261.

[2] 童慧思，张颢，孟华东，等. PHD滤波器在多目标检测前跟踪中的应用[J].电子学报，2011，39(9):2046-2051. TONG Hui-si, ZHANG Hao, MENG Hua-dong, et al. Probabilty Hypothesis Density Filter Multitarget Track-Before-Detect Application [J]. Acta Electuonica Sinica,2011, 39(9):2046-2051.

[3] MAHLER R P S. Multitarget Bayes Filtering via First-Order Multitarget Moments[J]. IEEE Transactions on Aerospace and Electronic Systems，2003，39(4)：1152-1178.

[4] 林晓东，朱林户，王瑛. 一种改进的基于概率假设密度滤波的多目标跟踪方法[J]. 控制与决策，2011，26(9)：1367-1372. LIN Xiao-dong, ZHU Lin-hu, WANG Ying. Improved Probability Hypothesis(PHD ) Filter for Multi-Target Tracking[J]. Control and Decision, 2011,26(9):1367-1372.

[5] 周卫东，张鹤冰，乔相伟. 基于核密度估计高斯混合PHD滤波的多目标跟踪算法[J]. 系统工程与电子技术，2011，39(9)：1932-1936. ZHOU Wei-dong, ZHANG He-bing, QIAO Xiang-wei. Multi-Target Tracking Algotithm Based on Kernel Density Estimation Gaussian Mixture PHD Filter[J]. System Engineering and Electronics, 2011,39(9)：1932-1936.

[6] 罗少华，徐晖，薛永宏. 一种新的SMC-PHD滤波的多目标状态估计方法[J]. 宇航学报，2011，32(10)：2187-2193. LUO Shao-hua, XU Hui, XUE Yong-hong. A Novel Multi-Target State Estimation Method for SMC-PHD Filter[J]. Journal of Astronautics,2011,32(10):2187-2193.

[7] VO B N, SONGH S, DOUCET A. Sequential Monte Carlo methods for Multi-Target Filtering with Random Finite Sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005,41(4):1224-1245.

[8] VO B N, MA W K. The Gaussian Mixture Probability Hypothesis Density Filter[J]. IEEE Transactions on Signal Processing，2006，54(11)：4091-4104.

[9] PUNITHAKUMAR K,KIRUBARAJAN T，SINHA A. A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-Before-Detect[C]∥SPIE，2005，5913:587-594.

[10] 林再平，周一宇，安玮，等.基于概率假设密度滤波平滑器的检测前跟踪算法[J].光学学报，2012，32(10)：1012003. LIN Zai-ping, ZHOU Yi-yu, AN Wei, et al. Track-Before-Detect Algorithm Base on Probability Hypothesis Density Smoother[J]. Acta Optica Sinica,2012,32,(10):1012003.

[11] XIANG Li, LIU Yu, SU Bao-ku. An Evolutionary Particle Filter Based EM Algorithm and Its Application[J]. Journal of Harbin Institute of Technology, 2010,17(1):70-74.

[12] 张慧，韩崇昭，闫小喜. 基于拟蒙特卡罗方法的概率假设密度多目标跟踪[J].控制与决策，2012，27(8)：1221-1225. ZHANG Hui, HAN Chong-zhao, YAN Xiao-xi. Probability Hypothesis Density Filter Based on Quasi-Monte Carlo Method for Multiple Target Tracking[J]. Control and Decision, 2012,27(8):1221-1225.

Multi-Target Track-Before-Detect Using Improved Probability Hypothesis Density Particle Filter

QIN Zhan-shi， ZHANG Zhi-jun,CHEN Wen, MA Ying

(AFEU,Aeronautics and Astronautics Engineering School,Shaanxi Xi’an 710038,China)

The existing track-before-detect technology based on probability hypothesis density has two shortcomings, i.e. lacking of accuracy in the number of target and high estimated error of cross target. An improved PHD-TBD method is put forward to deduce an updated accurate expression of the particle weight of the PHD-TBD algorithm, achieving the precise estimation of the number of the targets. The proposed algorithm fits the distribution of the resampled particles of the PHD-TBD via Gaussian mixture models (GMM), of which the component parameters can indicate the states of the targets. Expectation maximum (EM) algorithm is respectively used to estimate the parameters of the mixture. The simulation results demonstrate that proposed algorithm can effectively estimate the number and states of the targets.

probability hypothesis density; particle filter; Gaussian mixture models; track-before-detect; multi-target

2014-05-20；

2014-06-16

秦占师(1989-)，男，山东菏泽人。硕士生，研究方向为雷达信号处理及工程应用。

通信地址：734100 甘肃省山丹县南湖路25号 E-mail：1258798725@qq.com

10.3969/j.issn.1009-086x.2015.04.026

TN953;TP301.6

A

1009-086X(2015)-04-0155-06