点与多边形或多面体的拓扑关系判断

翟 艳，徐卫亚，张 强

（河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京210098）

0 引 言

点与多边形或多面体的拓扑关系判断方法，目前主要有射线法，叉积判断法，角度和法和面积法 （体积法）［1－3］。对简单的多边形，这些方法虽然都有各自的局限性，但通常可做出正确判断，而对复杂的多边形，尤其当射线过多边形的拐点或射线与多边形的某部分边界重合时易出现奇异情况，此时传统方法不能正确判断点与多边形的拓扑关系［4］。为解决此问题，一些学者对传统方法进行改进，也有在传统方法基础上提出新的判断方法。文献 ［5］从点与角的最短距离入手，找出与点距离最小的边，通过扫描确定唯一关联边作为判断依据，利用该边的两个角与点的位置关系判断点与多边形的位置关系，但该法在确定有效关联边时过程复杂；文献 ［6］利用直线的正负性判断点与多边形的位置关系，但该法只是减少求交点的数量，未对射线法中存在的奇异情况给出判断；文献 ［7］引入方向因子和方向边，通过确定由点与方向边得到的方向因子判断点与多边形的位置关系，该算法计算步骤复杂，判断过程繁琐；文献 ［8］克服传统射线法初始射线选择有太大主观性不足，找到多边形所有顶点在某区域的最小斜率点，利用该点确定初始判断射线。但该法仅对简单多边形适用性较好，对复杂多边形效果不尽人意。

针对目前改进方法存在的问题，本文在传统射线法的基础上引入虚交点的概念，对其进行改进，改进后的射线法可以解决传统方法在处理奇异情况时存在的问题，并通过运用切割剖面法将该方法应用到空间点与多面体拓扑关系的判断中。

1 传统射线法基本原理

传统射线法是判断点与多边形位置关系的常用方法，其基本原理请参见文献 ［2］。图1（a）中，P1点与多边形有两个交点，在多边形外部；P2点与多边形有一个交点，在多边形内部。对于简单多边形与点的位置关系，该判别方法结果准确。但对于如图1（b）所示的复杂多边形而言，根据传统射线法不能正确地判断点与多边形的拓扑关系。如图1（b）所示，点P1与多边形有4个交点，根据传统的射线法判断得到点P1在多边形外部，实际点P1却在多边形内部。故传统射线法在判断点与复杂多边形拓扑关系时存在不足。经研究发现，若过点P的射线通过多边形的顶点时，传统的射线法可能做出错误的判断，主要是因为射线与多边形的交点总数的统计方法不能满足这些情况。

图1 图形实例

2 改进射线法基本原理

本文中的多边形节点排列顺序为逆时针或者顺时针，改进射线法的实现步骤如下：

步骤1 判断点P是否位于多边形边界上，若点P位于边界上，返回点P位于多边形边界上，否则，执行步骤2至步骤4。

根据多边形顶点排列顺序，从第一个顶点开始依次连接多边形相邻的顶点，将多边形拆分为一些线段。遍历所有线段，判断点P是否位于线段上，若点P位于某条线段上，则点P位于多边形的边界上。

步骤2 按照传统的射线法计算过点P的射线与多边形的交点总数inter＿point＿total。对所有的线段进行循环，求解过点P的水平向右 （或铅垂线）射线与线段的交点（在端点处的交点除外）总数Num1；在循环过程中，对每个交点进行判断，若该交点位于线段的某个端点，则Num2＝Num2＋1；Num2表示射线与多边形线段相交在端点处的交点个数。则过点P的射线与多边形的交点总数inter＿point＿total＝Num1＋Num2。

步骤3 计算过点P的射线与多边形的虚交点总数virtual＿inter＿point＿total。

若过点P的射线与多边形的某个交点为多边形的某些顶点，在某些情况下，这些交点的一部分或全部为虚交点。下面具体说明虚交点的计算过程：

以过点P的水平向右的射线为例，根据多边形的顶点排列顺序，从第一个顶点开始判断，若某个顶点V（m）的Y坐标值与点P的Y坐标值相等，则从顶点V（m＋1）依次查找与点P的Y坐标相同的顶点个数Num3，判断顶点V（m－1）和V（m＋Num3＋1）与射线的关系，若这两个顶点位于射线的上下侧，则顶点 V（m＋1）到V（m＋Num3）为虚交点，virtual＿inter＿point＿total＝virtual＿inter＿point＿total＋Num3，若这两个顶点位于射线的同一侧，则顶点V（m）到V（m＋Num3）为虚交点，virtual＿inter＿point＿total＝virtual＿inter＿point＿total＋Num3＋1；从顶点V（m＋Num3＋2）继续进行判断，将虚交点的总数virtual＿inter＿point＿total进行累加，直到所有顶点全部判断完毕。

步骤4 计算过点P的射线与多边形的真实交点总数real＿inter＿point＿total。

对于无孔洞的多边形，通过执行步骤1至步骤4判断点与多边形的拓扑关系。首先执行步骤1判断点P是否位于边界上，若点P位于边界上，返回点P位于边界上，否则，执行步骤2至步骤4求解过点P的射线与该多边形的真实交点的总数，real＿inter＿point＿total＝inter＿point＿total－virtural＿inter＿point＿total，若real＿inter＿point＿total为奇数，则返回点P位于多边形内部，否则，返回点P位于多边形外。

对于还有孔洞的多边形，需要对其内部边界和外部边界分别执行步骤1至步骤4。首先执行步骤1来判断点P是否位于内部边界或外部边界上。若点P位于多边形内边界或外边界上，返回点P位于多边形的边界上。否则，执行步骤2至步骤4求解过点P的射线与内边界多边形的真实交点总数real＿inter＿point＿total1和所有外部多边形的真实交点总数real＿inter＿point＿total2，射线与多边形边界的真实交点总数real＿inter＿point＿total＝real＿inter＿point＿total1＋real＿inter＿point＿total2；若real＿inter＿point＿total为奇数，返回点P位于含孔洞多边形的内部，否则，返回点P位于含孔洞的多边形外部。

3 算例验证

下面分别给出点与无孔洞的多边形和有孔洞的多边形的拓扑关系的算例以验证上述改进射线法的正确性。

对于无孔洞多边形如图2（a）所示，图示无孔洞多边形有11个顶点V1～V11，共有11条线段。

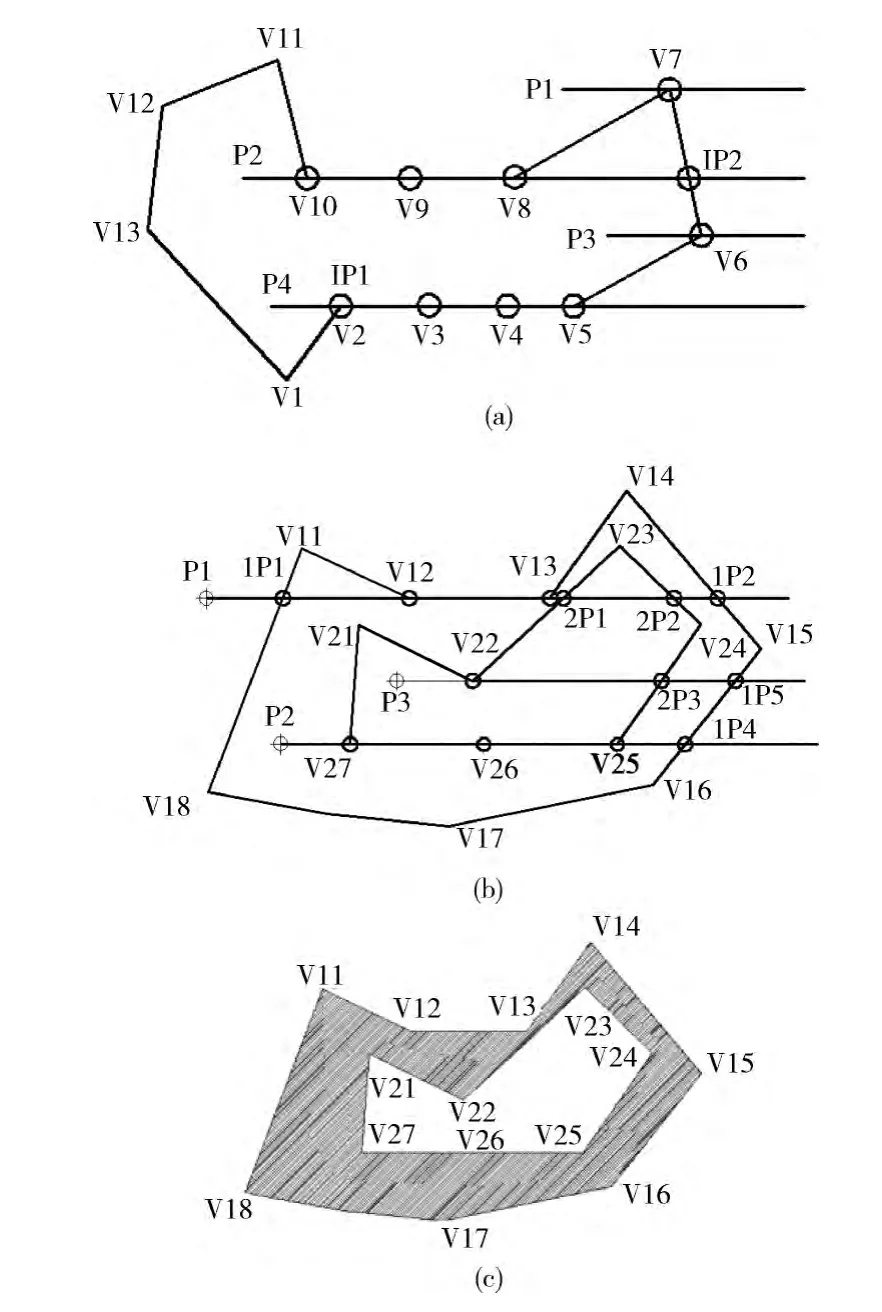
图2 复杂多边形算例

（1）P1点：

步骤1 P1不在多边形边界上；

步骤2 Num1＝0；Num2＝1；inter＿point＿total＝Num1＋Num2＝1；

步骤3 多边形顶点V8和V6在射线的同一侧，V7为虚交点，故virtual＿inter＿point＿total＝1；

步骤4 real＿inter＿point＿total＝inter＿point＿totalvirtural＿inter＿point＿total＝1－1＝0；

P1点位于多边形外部。

（2）P2点：

步骤1 P2不在多边形边界上；

步骤2 Num1＝1；Num2＝3；inter＿point＿total＝Num1＋Num2＝4；

步骤3 Num3＝2，多边形顶点V11和V7在射线的同一侧，V8～V10均为虚交点，故virtual＿inter＿point＿total＝3；

步骤4 real＿inter＿point＿total＝inter＿point＿totalvirtural＿inter＿point＿total＝4－3＝1；

P2点位于多边形内部。

（3）P4点：

步骤1 P2不在多边形边界上；

步骤2 Num1＝0；Num2＝4；inter＿point＿total＝Num1＋Num2＝4；

步骤3 Num3＝3，多边形顶点V1和V6在射线的异侧，V3～V5均为虚交点，故virtual＿inter＿point＿total＝3；

步骤4 real＿inter＿point＿total＝inter＿point＿totalvirtural＿inter＿point＿total＝4－3＝1；

P4点位于多边形内部。

对于有孔洞多边形如图2（b）所示。其中图2（c）所示阴影部分为有孔洞多边形的内部。

（1）P1点：内边界

步骤1 P1不在多边形内边界上；

步骤2 Num1＝2；Num2＝0；inter＿point＿total＝Num1＋Num2＝2；

步骤3 Num3＝0，virtual＿inter＿point＿total＝0；

步骤4 real＿inter＿point＿total1＝inter＿point＿total－virtural＿inter＿point＿total＝2－0＝2；

外边界：

步骤1 P1不在多边形外边界上；

步骤2 Num1＝2；Num2＝2；inter＿point＿total＝Num1＋Num2＝4；

步骤3 Num3＝1，多边形顶点V11和V14在射线的异侧，V12～V13均为虚交点，故virtual＿inter＿point＿total＝2；

步骤4 real＿inter＿point＿total2＝inter＿point＿total－virtural＿inter＿point＿total＝4－2＝2；

real＿inter＿point＿total＝real＿inter＿point＿total1＋real＿inter＿point＿total2＝4；

P1点位于多边形外部。

（2）P2点：内边界

步骤1 P2不在多边形内边界上；

步骤2 Num1＝0；Num2＝3；inter＿point＿total＝Num1＋Num2＝3；

步骤3 Num3＝2，V21和V24位于射线同侧，V25～V27均为虚交点，故virtual＿inter＿point＿total＝3；

步骤4 real＿inter＿point＿total1＝inter＿point＿total－virtural＿inter＿point＿total＝3－3＝0；

外边界：

步骤1 P2不在多边形外边界上；

步骤2 Num1＝1；Num2＝0；inter＿point＿total＝Num1＋Num2＝1；

步骤3 Num3＝0，virtual＿inter＿point＿total＝0；

步骤4 real＿inter＿point＿total2＝inter＿point＿total－virtural＿inter＿point＿total＝1－0＝1；

real＿inter＿point＿total＝real＿inter＿point＿total1＋real＿inter＿point＿total2＝1；

P2点位于多边形内部。

（3）P3点：内边界

步骤1 P3不在多边形内边界上；

步骤2 Num1＝1；Num2＝1；inter＿point＿total＝Num1＋Num2＝2；

步骤3 Num3＝0，V21和V23位于射线同侧，V22为虚交点，故virtual＿inter＿point＿total＝1；

步骤4 real＿inter＿point＿total1＝inter＿point＿total－virtural＿inter＿point＿total＝2－1＝1；

外边界：

步骤1 P1不在多边形外边界上；

步骤2 Num1＝1；Num2＝0；inter＿point＿total＝Num1＋Num2＝1；

步骤3 Num3＝0，virtual＿inter＿point＿total＝0；

步骤4 real＿inter＿point＿total2＝inter＿point＿total－virtural＿inter＿point＿total＝1－0＝1；

real＿inter＿point＿total＝real＿inter＿point＿total1＋real＿inter＿point＿total2＝2；

P3点位于多边形外部。

经无孔洞多边形和有孔洞多边形与点的拓扑关系实例验证可知，本文提出的基于改进射线法的点与多边形的拓扑关系快速判别方法具有相当的准确性。

4 点与多面体的拓扑关系判断

相比于平面内点与多边形的拓扑关系判断，空间点与多面体的拓扑关系判断更难。对于简单的多面体来说，可以用射线法准确地判断点与多面体的拓扑关系，但对于复杂的多面体来说，射线法不能给出正确的结果［9，10］。本文利用切割剖面法将三维问题转化为二维问题，即将点与多面体的拓扑关系判断转化为点与多边形的拓扑关系判断。其具体思想如下：

步骤1 过点P做平行于某个坐标平面，求得该平面与多面体边界的交线。

本文中所述的多面体的边界由三角形和四边形构成；因此求解平面与多面体边界的交线的实质是求解平面与三角形和四边形的交线，为了编程方便可以将四边形转化为两个三角形形。

对于不含孔洞的多面体来说，多面体的只有一个外边界，边界单元面的属性标记为外；对于含孔洞的多面体来说；多面体有内边界和外边界组成，外部边界单元面的属性标记为外；内部单元面的属性标记为内。若平面与某个单元面相交 （交线为线段），标记该交线的边界属性与单元面的属性一致。

步骤2 根据交线的边界属性，将其分为外边界交线和内边界交线，并将内边界交线和外边界交线均转化为节点排列有序的内边界多边形和外边界多边形。

步骤3 利用改进后射线法，判断点P与多边形的拓扑关系，根据点与多边形的拓扑关系确定点与多面体的拓扑关系。

若点P位于多边形上，则点P位于多面体的边界上。对于不含孔洞的多面体来说，若点P位于外边界多边形内部，则点P位于多面体内部；若点P位于外边界多边形外，则点P位于多面体外部。对于含孔洞的多面体来说，若点P位于内边界多边形内部，则点P位于多面体外部；若点P位于外边界多边形内，同时位于内多边形外，则点P位于多面体内部。

5 结束语

（1）在判定点与多边形拓扑关系的传统射线法的基础上，引入虚交点的概念对其进行改进，解决了传统射线法在判断点与复杂多边形拓扑关系，尤其是射线经过多边形顶点时存在的不足，并分别经有孔洞和无孔洞多边形与点的拓扑关系实例验证，结果表明本文提出的方法判断结果准确，简单易行，可操作性强。

（2）不同于传统体积法判断点与多面体的拓扑关系，本文利用切割剖面法将点与多面体的拓扑关系判断转化为点与多边形的拓扑关系判断，避免了传统体积法难于计算多面体体积的问题。

［1］CHEN Zhengyang，WANG Liqing，CHEN Shuqiang.Method of point inclusion test for simple polygons based on forked point［J］.Computer Engineering，2007，33 （17）：239－240 （in Chinese）.［陈正阳，王丽青，陈树强.基于单调链的判断点是否在多边形内的方法 ［J］.计算机工程，2007，33 （17）：239－240.］

［2］WANG Yanping，LIU Yonghe.The algorithm of using the method of radial to judge the points in flat in and out of the polygon ［J］.Shanxi Architecture，2007，33 （33）：364－365 （in Chinese）.［王燕平，刘永和.射线法判断平面中的点在多边形内外的算法 ［J］.山西建筑，2007，33 （33）：364－365.］

［3］CHEN Ruiqing，ZHOU Jian，YU Lie.Fast method to determine spatial relationship between point and polygon ［J］.Journal of Xi’an Jiaotong University，2007，41 （1）：59－63 （in Chinese）.［陈瑞卿，周健，虞烈.一种判断点与多边形关系的快速算法［J］.西安交通大学学报，2007，41 （1）：59－63.］

［4］LIU Liang.An optimized algorithm to determine topo－relation between point and polygon and clockwise or anti－clockwise in polygon ［J］.Geomatics ＆Information Technology，2007，30（1）：84－86 （in Chinese）.［刘梁.点、多边形拓扑关系与多边形顺、逆判断优化算法 ［J］.测绘与空间地理信息，2007，30（1）：84－86.］

［5］CHEN Jinlin，LIU Xiejin，LI Ning.New algorithm for determining position relation between simple polygon and point ［J］.Journal of Huainan Normal University，2012，14 （5）：120－122（in Chinese）.［陈金林，刘谢进，李宁.点与简单多边形位置关系判别新算 ［J］.淮南师范学院学报，2012，14 （5）：120－122.］

［6］HAO Jianqiang，GONG Yunzhan，YE Hong.Stable serial optimal and parallel algorithm of point－in－polygon test ［J］.Application Research of Computers，2010，27 （4）：1342－1348（in Chinese）.［郝建强，宫云战，叶红.点与多边形位置检测的串行最优与并行的算法 ［J］.计算机应用研究，2010，27（4）：1342－1348.］

［7］ZHANG Ka，SHENG Yehua，YE Chun.Algorithm of polygon point in－out test based on direction factor and direction edge［J］.Science of Surveying and Mappong，2010，35 （4）：174－176（in Chinese）.［张卡，盛业华，叶春.基于方向因子和方向边的多边形内外点判断算法 ［J］.测绘科学，2010，35（4）：174－176.］

［8］DONG Xiushan，LIU Runtao.New algorithm for determining position relation between simple polygon and point ［J］.Computer Engineering and Applications，2009，45 （2）：185－186 （in Chinese）.［董秀山，刘润涛.判断点与简单多边形位置关系的新算法［J］.计算机工程与应用，2009，45 （2）：185－186.］

［9］SHI Lu，BAI Bing，LI Xiaochun.New algorithm to judge the relation of spatial location between point and polyhedron［C］／／The Tenth National Exhibition of Rock Mechanics and Engineering Academic Conference Proceedings，2008：295－298（in Chinese）.［石露，白冰，李小春.判断点与多面体空间位置关系的一个新算法 ［C］／／第十届全国岩石力学与工程学术大会论文集，2008：295－298.］

［10］WU Bofeng，LIN Jiaxiang，WANG Weibin.The research on judging topological relationships between a point and a polyhedron ［J］.Journal of Fuzhou University （Natural Science），2010，38 （5）：634－639 （in Chinese）.［吴博峰，林甲祥，王伟斌.点与多面体空间拓扑关系的判定研究 ［J］.福州大学学报 （自然科学版），2010，38 （ 5）：634－639.］