基于双二阶广义积分锁频环的风电并网控制系统仿真

谢聪， 吴新开， 雷雅云， 唐明淼(湖南科技大学 信息与电气工程学院，湖南 湘潭 411201)

基于双二阶广义积分锁频环的风电并网控制系统仿真

谢聪， 吴新开， 雷雅云， 唐明淼
(湖南科技大学 信息与电气工程学院，湖南 湘潭 411201)

通过采用双二阶广义积分器实现风力发电并网系统的锁相，检测出不对称电网电压中的正序分量和负序分量。因为电网频率比电网相角更加稳定，所以使用双二阶广义积分锁频环对风力发电系统进行并网。利用MATLAB/Simulink软件对基于双广义二阶积分锁相环和锁频环的风力发电并网系统进行仿真，仿真结果证明锁频环比锁相环具有更加平滑的响应，验证了控制系统的可行性和有效型，保证了风力发电系统的顺利并网。

风力发电；双二阶广义积分器；锁相；锁频环；仿真

0 引 言

近年来，资源枯竭的窘境愈发明显，而风能是一种清洁、安全的选择[1]。实际应用中，风能具有不稳定性，风力发电机发出的电压频率、幅值、相位都是会随时发生变化的，所以，风电并网技术十分重要。

三相变换器并网依赖于高性能的检测系统，尤其需要设计快速而准确消除高次谐波并检测出电压向量各序分量的方法。三相电力网络中电压向量各序分量的实时检测是分布式发电、储能系统、柔性交流输配电、电力线路调整器和不间断电源控制的关键问题[2-3]。采用双二阶广义积分器的正/负序分量计算模块(PNSC)实现正序分量和负序分量的分离输出。

在实现风力发电系统并网时，需要对系统实行精确锁相。传统的过零点检测三相电压相位法，由于网侧电压在过零点存在毛刺，检测会存在很大的误差。文献[4]提出的单同步坐标锁相环不能实现对三相不平衡电压的精确锁相。文献[5]提出的双同步参考坐标系锁相环虽然在不对称故障下仍能保证准确的电网同步，但是其解耦结构主要针对消除负序基频分量影响，因此其抵抗低次谐波扰动能力比较弱。本系统应用基于双二阶广义积分[6-7]锁相锁频环技术。

1 三相并网逆变器[8]的数学模型

三相逆变并网的主电路拓扑结构如图1所示，其中e1、e2、e3为三相电网电压，i1、i2、i3为三相变换器输出电流，v为直流电压源，d1-d6是6个IGBT，R、L分别为滤波器的电阻和电感。

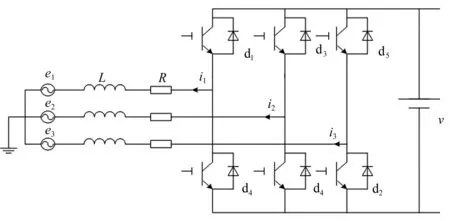
图1 三相逆变并网主电路拓扑结构

在abc三相静止坐标系下的数学模型[9]:

(1)

abc三相静止坐标系变为αβ两相静止坐标系的变换矩阵：

(2)

abc三相静止坐标系变为dq两相旋转坐标系，采用如下的变换矩阵:

(3)

变换后，在两相旋转坐标系下的数学模型为：

(4)

2 基于双二阶广义积分锁频环的方法

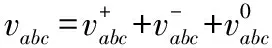
(5)

(6)

(7)

式中a是Fortescue 算子的特殊形式，表示在瞬时正弦输入信号中加入基波频率的相移，值为120°相移。

在三相并网变换器中，研究主要集中于注入电流的正序、负序分量控制。vabc的各序分量可通过式(2)中变换矩阵表示，因此有:

(8)

将式(5)代入式(6)中，可以得到:

(9)

(10)

最后，通过运算这些矩阵，可得到以下表达式：

(11)

(12)

式中q(q=e-jw/2)是一个90°滞后的移相运算，将其应用于时域，可获得输入波形的交轴分量。

2.1 双二阶广义积分器三相锁相环

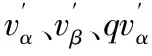
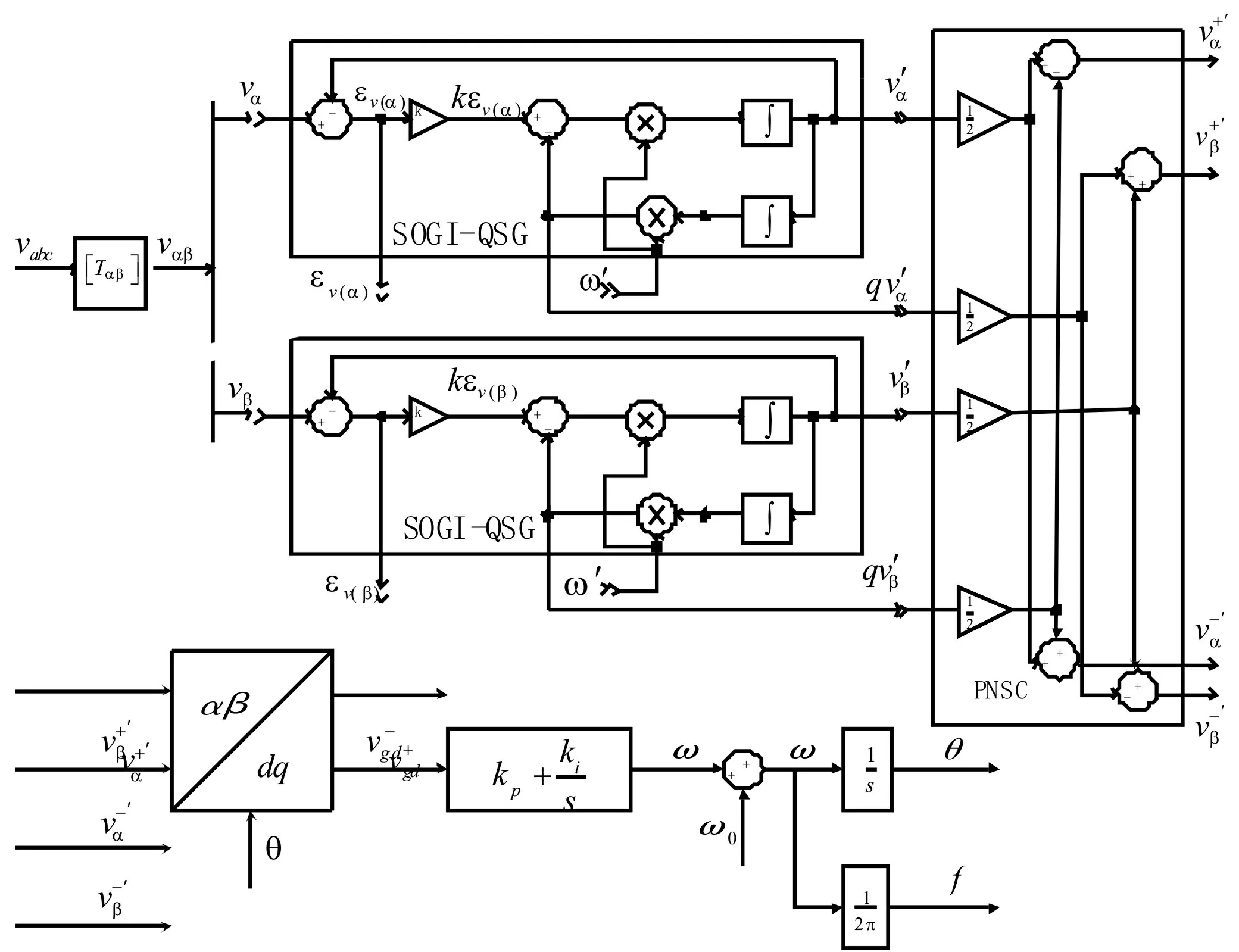
图2 双二阶广义积分锁相环(DSOGI-PNSC-PLL)结构图

通过双二阶广义积分器获得的从不对称输入电压向量到正序分量的传递函数为：

(13)

由于电网频率比电网相角更加稳定，在双二阶广义积分解耦三相锁相系统中，频率反馈环和相位反馈环是相互交错的，会有系统响应超调大和稳定时间过长的缺点，因此采用锁频环代替锁相环。

2.2 双二阶广义积分器锁频环

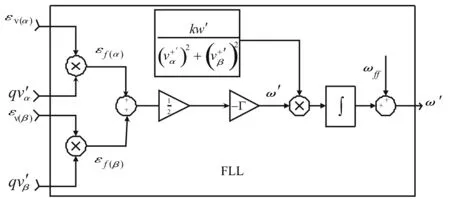
图3 基于双二阶广义积分器的锁频环(DSOGI-PNSC-FLL)结构

双二阶广义积分器锁频环系统中两个输入信号vα和vβ具有相同的频率，使用一个锁频环结构图如图3，其中α和β信号发生器所产生频率误差信号可通过计算平均误差信号的方法进行合并：

(14)

双二阶广义积分器锁频环实现了αβ参考坐标上三相电压的对称分量解耦估计，同时也实现了电网频率的估计。

3 系统性能仿真

3.1 算法仿真比较

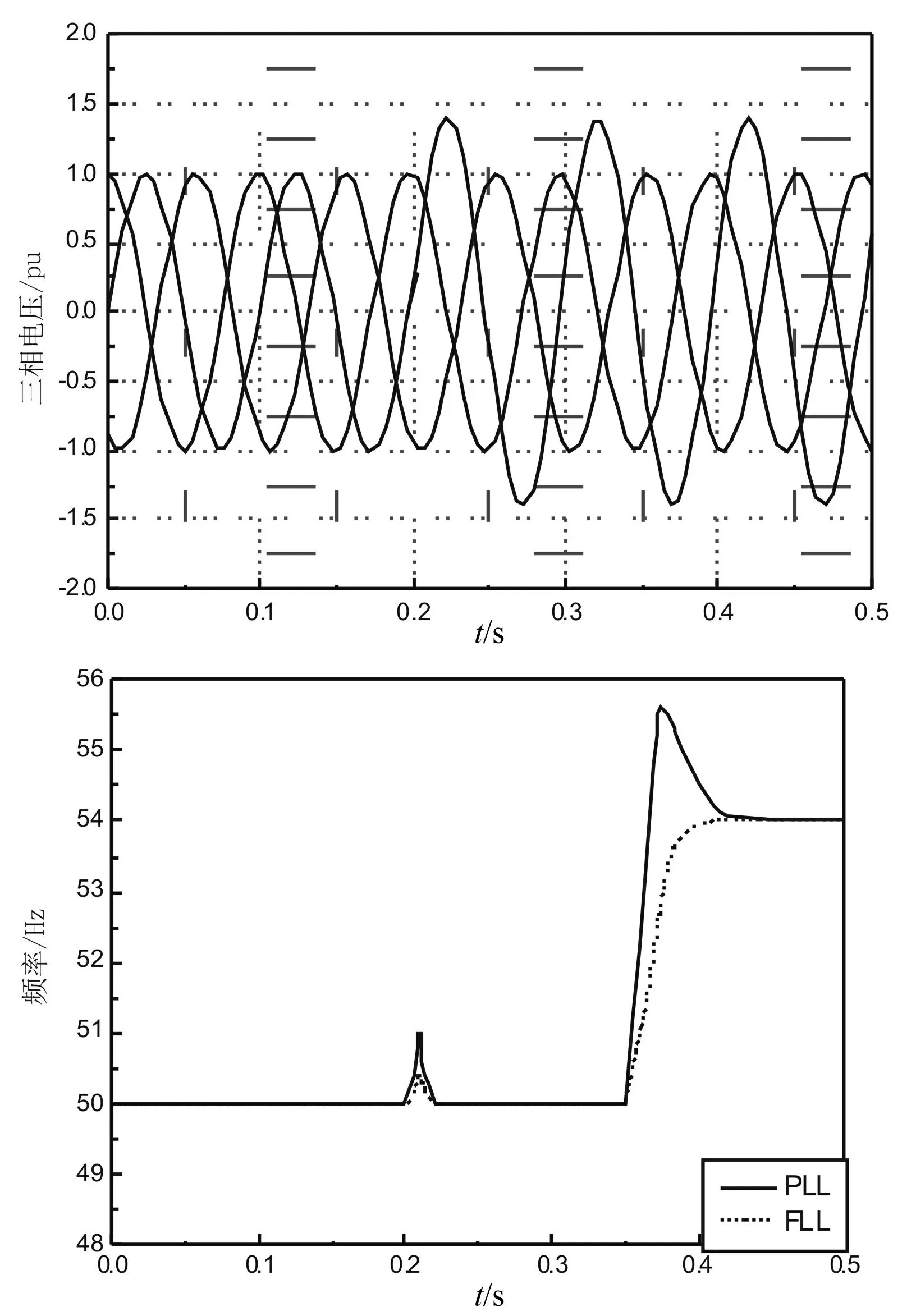
图4 锁频环与锁相环仿真方式对比

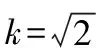
从图4仿真结果可得：在系统的动态过程中，采用锁频环方式的超调量比采用锁相环方式要小，且其稳定时间比锁相环方式要短；在电网故障情况下，两种方式都能频率自适应性，频率精度高。可见锁频环方式具有超调量小，稳态精度高，稳定时间短，频率自适应性强的优点，从而提高了风电并网的有效性和可靠性。

3.2 基于双二阶广义积分锁频环算法仿真

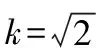
由二阶广义积分器锁频环所检测到的各相序的幅值和相角计算为:

(15)

系统仿真图如图5所示。

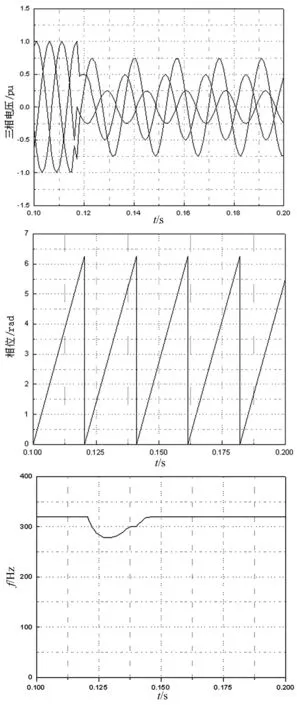
图5 三相不对称输入电压下的输出相位和输出频率

图5中的第一个图显示了三相不对称电压,第二个图为不对称输入电压下检测到的正序分量相角和实际相角,该图显示双二阶广义积分器锁频环完全消除了检测得到相角中的稳态误差，第三个图显示了锁频环所测得的频率,从图中可以看出检测到的频率无高频振荡现象。因此，从仿真结果可以看出，控制系统采用基于双二阶广义积分锁频环的控制策略，在电网不对称电压条件下能精确的检测电网电压的相位和频率信息，检测到的频率无高频振荡现象，频率自适应性强。依据本文中的控制系统，当电网电压不对称时，仍然能够并入电网，从而提高了电网的可靠性和有效性。

4 结束语

风力发电的发展，实现风力发电的顺利并网越来越重要，尤其是在三相电压不对称的条件下的风电并网。本文从三相逆变并网主电路出发，应用双广义二阶积分锁频环实现风电系统的精确锁相，使得在三相电压不对称时仍能快速、准确的跟踪频率和相位信息，具有很好的频率自适应性。

[ 1 ] 王晓蓉,王伟胜,戴慧珠,等.我国风力发电现状与展望[J]].中国电力, 2004,31(2): 81-84.

[ 2 ] CICHOWLAS M, MALINOWSKI M, KAZMIERKOWSKI M P, et al. Active filtering function of three-phase PWM boost rectifier under different line voltage conditions[J]. Industrial Electronics, IEEE Transactions on, 2005, 52(2): 410-419.

[ 3 ] TEODORESCU R, BLAABJERG F. Flexible control of small wind turbines with grid failure detection operating in stand-alone and grid-connected mode[J]. Power Electronics, IEEE Transactions on, 2004, 19(5): 1323-1332.

[ 4 ] YOUNG K, DOUGAL R A. SRF-PLL with dynamic center frequency for improved phase detection[C]//Clean Electrical Power, 2009 International Conference on. IEEE, 2009: 212-216.

[ 5 ] RODRIGUEZ P, POU J, BERGAS J, et al. Decoupled double synchronous reference frame PLL for power converters control[J]. Power Electronics, IEEE Transactions on, 2007, 22(2): 584-592.

[ 6 ] 刘述奎,韩莹,李奇,等. 基于双二阶广义积分锁相环的燃料电池并网系统研究[J]. 电力系统保护与控制,2014,42(5):122-128.

[ 7 ] 刘锋. 电网不平衡下三相锁相环研究[D].成都：电子科技大学,2013.

[ 8 ] 杨勇,赵方平,阮毅,等. 三相并网逆变器模型电流预测控制技术[J]. 电工技术学报,2011,26(6):153-159.

[ 9 ] 周京华,刘坤,李正熙. 三相电压源型PWM整流器的DSP控制[J]. 电气传动,2008,50(6):27-30，51.

[10] RODRIGUEZ P, LUNA A, CIOBOTARU M, et al. Advanced grid synchronization system for power converters under unbalanced and distorted operating conditions[C].IEEE Industrial Electronics, IECON 2006-32nd Annual Conference on. IEEE, 2006: 5173-5178.

[11] RODRIGUEZ P, LUNA A, CANDELA I, et al. Multi-resonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J]. Industrial Electronics, IEEE Transactions on, 2011, 58(1): 127-138.

Simulation of the Control System of Wind Power IntegrationBased on Double Second-order Generalized Integral Frequency-locking Loop

XIE Cong,WU Xin-kai, LEI Ya-yun, TANG Ming-miao
(College of Information and Electrical Engineering,Hunan University of Science and Technology, Xiangtan Hunan 411201, China)

The double second-order generalized integrator is adopted to realize phase locking of the wind power integration system, and positive and negative sequence components of the asymmetric grid voltage are detected. As the frequency of the grid is more stable than its phase angle, the double second-order generalized integral frequency-locking loop is chosen for grid-connection of the wind power generation system. Matlab/simulink software is used to simulate the wind power integration system based on the double second-order generalized integral phase-locking loop and frequency-locking loop. The simulation results verify that the response of the frequency-locking loop is smoother than that of the phase-locking loop and that the control system is feasible and effective, ensuring the smooth integration of the wind power generation system.

wind power generation;double second-order generalized integrator; phase lock; frequency-locking loop;simulation

10.3969/j.issn.1000-3886.2015.05.015

TM614

A

1000-3886(2015)05-0047-03

谢聪(1989-)，女，湖南娄底人，硕士生，主要研究方向为电力电子及风力发电并网技术。 吴新开(1956-)，男，湖南娄底人，教授，主要研究方向为电力电子与电气传动，半导体制冷技术、绿色能源及无损检测技术。 雷雅云(1991-)，女，湖南常德人，硕士生，主要研究方向为新能源转换与控制。

定稿日期: 2014-10-24