HTR-PM反应堆保护系统软件可靠性增长模型的研究
2015-05-04刘瑜,李铎,郭超
刘 瑜,李 铎,郭 超
(清华大学 核能与新能源技术研究院,先进核能技术协同创新中心,先进反应堆工程与安全教育部重点实验室,北京 100084)
HTR-PM反应堆保护系统软件可靠性增长模型的研究
刘 瑜,李 铎,郭 超
(清华大学 核能与新能源技术研究院,先进核能技术协同创新中心,先进反应堆工程与安全教育部重点实验室,北京 100084)
研究数字化反应堆保护系统软件的可靠性对提高保护系统的整体可靠性具有重要的意义。本文在分析、整理HTR-PM保护系统软件开发过程中记录的测试数据基础上,研究并提出了基于错误严重程度的软件可靠性模型。软件测试过程中不同严重程度的错误其检测难度不同,导致检测率随时间的变化趋势不同,本文提出了严重程度比函数的概念以表述这一现象,并对不同严重程度错误的检测数据分别建模,使软件可靠性模型的预测结果更具有工程应用价值。
反应堆保护系统;软件可靠性;错误严重程度;软件可靠性增长模型
反应堆保护系统是核电厂仪表与控制(I&C)系统中最重要的系统之一。随着技术的发展,数字化系统的技术优势(如容错、自检、信号确认、系统诊断等)日益突显出来,过去的模拟保护系统已逐步被数字化保护系统所替代[1]。由于系统中软件的存在,数字化保护系统具有完全不同的失效原因和失效模式。研究数字化保护系统软件的可靠性具有重要意义。
对于软件可靠性的研究,国内外学者已发表了近百种软件可靠性的评估方法,其中时间域方法被认为是应用最广的方法[2]。时间域方法是对过去的失效数据建模,以预测未来。该方法使用单位时间内的软件失效次数或软件的失效间隔时间(用日历时间和计算机执行时间测量)两种数据,基于这些数据,前人已建立了很多数学模型来估计软件的失效率、平均失效时间、可靠性等。由于软件可靠性随着测试的进行逐渐增加,所以这些基于时域的模型又称为软件可靠性增长模型(SRGM)。虽然已有很多相关的可靠性模型被提出和研究,但这些模型的前提假设因为研究对象的不同而有所差别,因此,没有一个模型能成功适用于所有场合。
本文以华能山东石岛湾核电厂高温气冷堆核电站示范工程(HTR-PM)保护系统[3-4]的软件为研究对象,在HTR-PM保护系统的软件开发过程中记录大量的测试数据,通过对这些数据的整理、分析和建模,研究和分析HTR-PM保护系统软件的可靠性增长模型。
1 HTR-PM保护系统软件的测试数据及分析
HTR-PM保护系统的软件开发过程中积累了大量的测试数据,这些数据反映了每个软件模块开发过程中检测到的错误及其消除的过程。从记录数据的构成来看,每个记录项包括3方面的信息,分别是反映错误发现位置的版本信息、属性信息和时间信息,如图1所示。
本文关注的是测试数据记录项中错误属性的严重程度,HTR-PM保护系统软件测试中对每个发现的错误都根据影响的严重程度不同进行等级划分,分为提示、一般、严重及致命4类。不同严重程度的错误除了对运行造成不同的损害,也会对软件测试过程产生不同的影响,如提示性错误是软件语句格式、变量命名方式等方面的错误,一般在软件的静态测试阶段就可检测出来,也较容易修改;严重性错误是不完全的逻辑、忽略了特殊数据边界等错误,需在软件的动态测试阶段设计大量的测试用例才能检查出来,且错误的修改也较麻烦。

图1 软件测试数据记录项的结构Fig.1 Data field of software test record
为简化研究模型,将HTR-PM保护系统软件测试中记录的错误类别归为2类:提示和一般类错误合并为非关键错误;严重和致命类错误合并为关键错误。同样以测试日为基本时间(剔除节假日的工作日)单位,统计两类错误随时间变化的累计错误数。按上述统计方法,HTR-PM保护系统软件模块A开发过程中记录的错误数据统计如图2所示(错误数是归一化后的统计数据)。
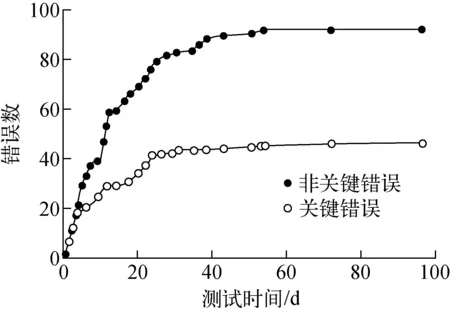
图2 软件模块A的测试数据统计Fig.2 Testing data statistics of module A
在传统的研究中,软件可靠性增长模型都是基于非齐次泊松过程,通过拟合错误检测的数据来寻找可刻画错误发现过程的均值函数,且大多数模型均默认每个错误具有相同的测试努力和策略[5-9]。如前所述,这一假设在实际的开发过程中并不完全成立,不同的错误,可能会经过不同的检测努力和策略才能从系统中移除。为描述这一现象,有些研究者将错误划分为不同的类型,并分别进行处理。Yamada等[10]提出一个改进的指数可靠性增长模型,假设有两种错误类型,各自的检测率呈现不同的指数曲线;Pham[11]进一步提出一个可描述多种类型错误的可靠性模型;Kapur等[12]提出了一般Erlang模型,建立3种可靠性模型分别拟合简单、困难、复杂3种错误类型。Tamura等[13]对JM模型进行扩展,从故障率的角度出发,将错误的故障率根据起因的不同划分为两类并分别归属以不同的变化趋势。这些软件可靠性模型研究中只对软件的错误进行了分类研究,未研究不同类别错误的相对变化趋势,即未将分类后的错误作为一个整体来研究。本文在研究HTR-PM保护系统软件的可靠性模型中提出严重程度比函数的概念,既考虑软件测试过程中不同严重程度的错误检测率随时间的变化趋势有所区别,同时对不同严重程度错误的数据进行建模,使软件可靠性模型的预测结果更具有工程应用价值。
2 考虑错误严重程度分类的软件可靠性模型
2.1 错误严重程度比函数
在HTR-PM保护系统软件测试过程中,关键错误与总错误数比的变化具有一定的规律性,如图3所示(图中数据取自HTR-PM保护系统软件中模块A的测试记录)。可看出,随着测试的进行,关键错误与总错误数的比近似呈指数递减。
为模拟这一变化,定义错误严重程度比函数(SRF)ρc(t)(c=1,2),它表征不同严重程度错误的检测率占总体检测率的比随时间的变化情况,ρ1(t)和ρ2(t)分别为关键错误比函数和非关键错误比函数。根据定义,ρc(t)需满足:
(1)
根据SRF的变化趋势(在测试的初始阶段,比例呈指数变化,之后由于潜在错误的减少,比例趋于饱和),可借助Logistic函数来描述这一变化。
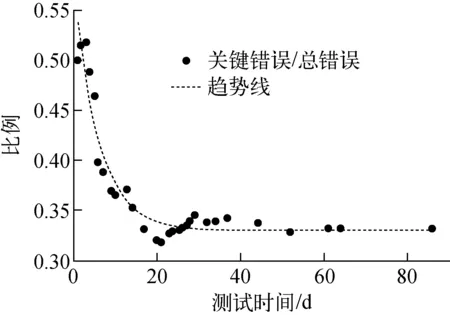
图3 测试过程中关键错误与总错误数比的变化趋势Fig.3 Ratio tendency of critical fault to total fault during testing
Logistic函数是一种S型曲线函数,借助Logistic函数,ρc(t)可表示为:
(2)
其中,α和β为Logistic函数的参数。式(2)中,当β接近于1或α接近于0时,ρc(t)近似于一条直线。
2.2 引入SRF的软件可靠性增长模型
为构建描述不同严重程度错误的可靠性模型构架,对经典软件可靠性增长模型的假设进行修改和补充,修改后的假设条件如下:1) 假设错误的检测过程是泊松过程,到时间t的累积检出错误数为N(t),则N(t)符合均值函数为m(t)的泊松分布,单位时间间隔内期望的错误检出数与该时间间隔内未检测出的错误数呈正比,因此,均值函数为有界非减时间函数;2) 软件中发现的错误依据其对失效的贡献程度划分为两类,即关键错误和非关键错误;3) 每个时间间隔检测出的错误数是相互独立的;4) 错误被发现后立刻修正,且不引入新的错误;5) 不同严重程度的错误,其在(t,Δt+t)的时间间隔内,期望的检测数与该间隔内未检测出的错误数所呈的比例不同。
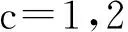
(3)
其中,b为错误检测模型中假设的期望检出率。
(4)
当ρc(t)为定值时,累积错误数的期望函数可简单地写为:
(5)
根据以上的假设,可建立考虑错误严重程度的可靠性增长模型,根据式(3),在Δt→0时,解微分方程可得到:
(6)
其中,τ为时间积分变量。
从而可解得该模型不同严重程度错误累计数的期望函数为:
(7)
2.3 错误严重程度分类模型的可靠性测度
根据非齐次泊松过程,可估计软件失效的可靠度。设Sj(j=1,2,…)表示第j个错误被检测到的时刻,Xj=Sj-Sj-1为相邻错误出现的间隔时间,则在Sk-1=t的前提下,Xk>x的条件概率即为软件的可靠度度量,则:
(8)
若到时刻t为止的累计错误个数N(t)服从均值为m(t)的非齐次泊松分布,则有:


(9)
对于不同严重程度的错误,可类似推导出其可靠度,即:
Rc(x|t)=exp(-(mc(t+x)-mc(t)))
(10)
2.4 参数估计
上述考虑错误严重程度分类的软件可靠性模型中含有N、b、α和β4个参数,在参数估计的研究中使用最小二乘法和最大似然估计法。
1) 最小二乘法
应用最小二乘法进行参数估计的优点为计算较为简单,但不能保证估计的无偏性,缺乏统计意义。其估计方程为:
(11)
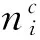
2) 最大似然估计法
最大似然估计法具有更好的统计意义,算式复杂,求解难度大。进行估计前,需将两组数据的记录时间转换为相同的间隔,即ti=τj(i=j=1,2,…,k1)。以泊松过程的联合概率函数为似然函数,可得到:
(12)
式中的m1(ti)+m2(ti)为整体期望累计错误数。最大似然估计法的区间估计可借助Fisher信息矩阵进行计算,具体可参阅文献[14]。
3 实例验证
实例验证使用如下方法:选取前部分数据(包括测试日和对应的累计错误数)作为拟合数据,应用参数估计方法得到可靠性模型的参数,基于可靠性模型可预测剩余的数据点。比较预测数据和实际数据间的平均方差和决定系数,可评价可靠性模型的误差。
(13)
决定系数R2体现了估计结果和实际数据的线性相关性,R2越大表明拟合的结果越好。
(14)
评判模型优劣的另一个依据是模型的预测性能,本文在选取部分数据进行参数拟合后进行一步预测(x=1),并选用相对误差作为比较的标准,则:
(15)
3.1 模型拟合结果的比较
将收集到的全部数据代入式(7),分别用最小二乘法和最大似然估计法进行参数估计,基于本文模型模块A的拟合结果如图4所示。可看出,最大似然估计法和最小二乘法均可较好地给出不同严重程度错误数的估计,对本文研究的数据对象均适用。从90%置信区间来看,最小二乘法的估计结果的推断带较窄,而最大似然估计法的结果更偏于保守。表1列出了模型参数估计和误差评价结果,从表1可看出,由于最小二乘法的模型拟合效果的MSEest较小而R2较大,因此其拟合效果更好。
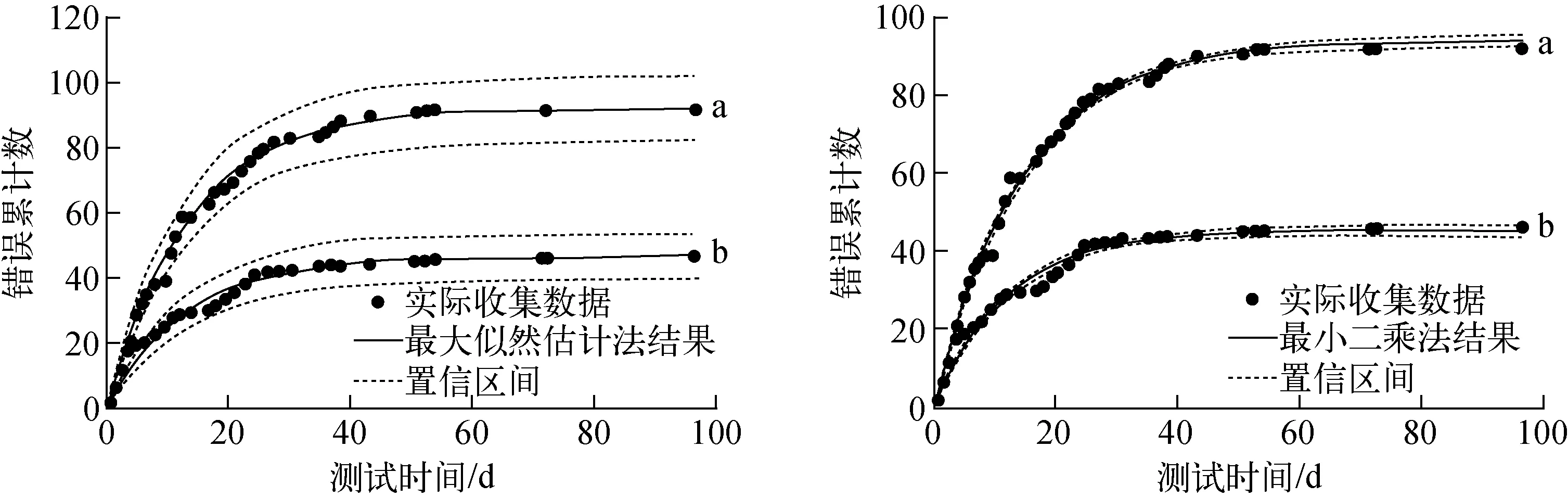
a——非关键错误拟合结果;b——关键错误拟合结果

表1 模型参数估计和误差评价结果Table 1 Model parameters estimation and error evaluation
3.2 模型预测结果的比较
为比较两种估计方法的预测性能,对数据进行变结点预测。使用部分数据,拟合模型并做出一步预测,图5所示为模型的预测误差。可看出,最大似然估计法得到的结果具有更低的预测误差,较最小二乘法而言,其在测试早期就已表现出更好的预测精度。
3.3 错误严重程度比函数的分析
根据表1中拟合效果更好的最小二乘法参数,可绘制关键错误比函数ρ1(t)的曲线,如图6所示,ρ1(t)随测试时间的增大呈指数衰减。
由图6可看出,测试后期HTR-PM保护系统软件中剩余的关键错误已很少,这与工程中软件测试的实际情况是一致的。本文定义的关键类型错误是严重影响软件功能的错误,因此关键错误往往更易在测试初期被检测到,这是因为在遍历测试用例时,大部分测试用例均将指向关键错误引起的失效,测试人员更易发现这些失效。保护系统的软件属于安全级软件,在软件的设计中对代码的编程规范增加了许多限制条件,防止软件不必要的复杂性,大部分关键类型错误的检测不需要设计复杂的测试用例,因此关键错误在测试后期已很少。
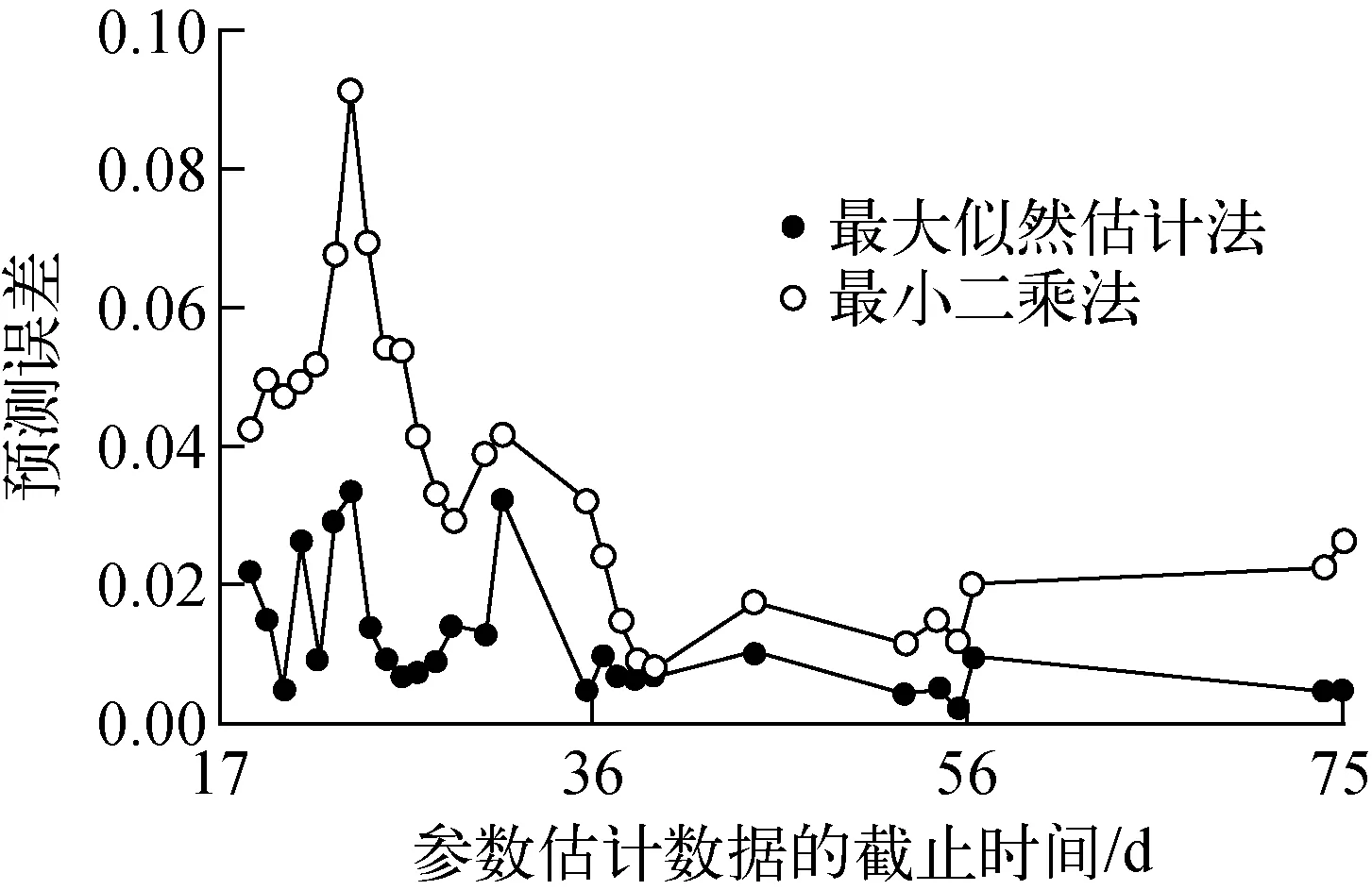
图5 模型的预测误差Fig.5 Prediction error of proposed model

图6 关键错误比函数曲线Fig.6 Curve of severity rate function of critical fault
4 结论
研究数字化保护系统软件的可靠性对提高保护系统的整体可靠性具有重要的意义,本文在分析、整理HTR-PM保护系统软件开发过程中记录的测试数据基础上,研究并提出了基于错误严重程度的软件可靠性模型。由于在实际测试过程中,不同严重程度的错误其检测的难度不同,导致检测率随时间的变化趋势有所区别,本文提出了错误严重程度比函数的概念以描述这种现象。考虑错误严重程度分类的软件可靠性模型在传统可靠性增长模型的基础上,将某一种错误的检测率转化为随时间变化的函数,使之更符合实际的测试过程。选用Logistic函数来拟合错误严重程度比函数,通过实验数据分析,其取得了较好的拟合和预测效果。
[1] ALDEMIR T, STOVSKY M P, KIRSCHENBAUM J, et al. Dynamic reliability modeling of digital instrumentation and control systems for nuclear reactor probabilistic risk assessments[M]. Washington, D. C.: Citeseer, 2007.
[2] LYU M R. Software reliability engineering: A roadmap[J]. IEEE Computer Society, 2007: 153-170.
[3] 郭超,李铎,熊华胜. 高温气冷堆示范工程反应堆保护系统故障树模型的建立和分析[J]. 原子能科学技术,2013,47(11):2 063-2 070.
GUO Chao, LI Duo, XIONG Huasheng, et al. Development and analysis of fault tree model of HTR-PM reactor protection system[J]. Atomic Energy Science and Technology, 2013, 47(11): 2 063-2 070(in Chinese).
[4] 李铎,熊华胜,郭超,等. HTR-PM 反应堆保护系统工程样机的研制[J]. 仪器仪表用户,2013,20(5):36-38.
LI Duo, XIONG Huasheng, GUO Chao, et al. Development of HTR-PM reactor protection system engineering prototype[J]. Electronic Instrumentation Customer, 2013, 20(5): 36-38(in Chinese).
[5] GOEL A L, OKUMOTO K. Time-dependent error-detection rate model for software reliability and other performance measures[J]. IEEE Transactions on Reliability, 1979, R28(3): 206-211.
[6] OHBA M. Inflection S-shaped software reliability growth model[M]∥Stochastic Models in Reliability Theory. Heidelberg: Springer, 1984: 144-162.
[7] HUANG C Y, LYU M R, KUO S. A unified scheme of some nonhomogenous poisson process models for software reliability estimation[J]. IEEE Transactions on Software Engineering, 2003, 29(3): 261-269.
[8] OKAMURA H, DOHI T, OSAKI S. Software reliability growth models with normal failure time distributions[J]. Reliability Engineering and System Safety, 2013, 116: 135-141.
[9] PHAM H. A new software reliability model with Vtub-shaped fault-detection rate and the uncertainty of operating environments[J]. Optimization, 2014, 63(10): 1 481-1 490.
[10]YAMADA S, OSAKI S, NARIHISA H. A software reliability growth model with two types of errors[J]. EDP Sciences, 1985, 19(1): 87-104.
[11]PHAM H. Software reliability assessment: Imperfect debugging and multiple failure types in software development[R]. Idaho: National Engineering Laboratory, 1993.
[12]KAPUR P, GROVER P, YOUNES S. Software reliability growth model with errors of different severity[J]. Computer Science and Informatics, 1995, 25: 51-65.
[13]TAMURA Y, YAMADA S. Reliability assessment based on hazard rate model for an embedded OSS porting-phase[J]. Software Testing Verification & Reliability, 2013, 23(1): 77-88.
[14]LAWLESS J F. Statistical models and methods for lifetime data[M]. New York: John Wiley & Sons, 2011.
Research on Software Reliability Growth Model of Reactor Protection System for HTR-PM
LIU Yu, LI Duo, GUO Chao
(InstituteofNuclearandNewEnergyTechnology,CollaborativeInnovationCenterofAdvancedNuclearEnergyTechnology,KeyLaboratoryofAdvancedReactorEngineeringandSafetyofMinistryofEducation,TsinghuaUniversity,Beijing100084,China)
The research on software reliability of digital reactor protection system (RPS) plays an important role to improve the reliability of RPS. Based on analyzing the fault data set collected during the software development of HTR-PM RPS, a new software reliability model involving the fault severity was studied and established. In the practice detecting faults with different severities usually have different levels of difficulty, and the trend of detecting rate with different severities varies with time. In this paper the severity ratio function (SRF) was proposed, and separate models were developed to deal with faults with different severities. This can achieve better prediction and reflect the software reliability in more aspects for engineering application.
reactor protection system; software reliability; fault severity; software reliability growth model
2014-06-18;
2014-09-28
国家科技重大专项资助项目(ZX06901);清华大学自主科研计划资助项目
刘 瑜(1990—),男,山东肥城人,硕士研究生,核科学与技术专业
TL36
A
1000-6931(2015)10-1870-06
10.7538/yzk.2015.49.10.1870
