时空中子动力学计算的刚性限制法
2015-05-04魏明哲李云召何明涛
魏明哲,李云召,何明涛
(西安交通大学 核科学与技术学院,陕西 西安 710049)
时空中子动力学计算的刚性限制法
魏明哲,李云召*,何明涛
(西安交通大学 核科学与技术学院,陕西 西安 710049)
随着中子动力学计算的精度要求以及计算条件的不断提高,如何更好地处理三维时空中子动力学方程的刚性问题对于提高计算效率具有非常重要的工程应用价值。本文应用刚性限制法处理方程组的时间变量,并与空间变量处理方法变分节块法相耦合建立了相应的时空中子动力学计算模型。基准题的数值计算结果表明,刚性限制法可与包括变分节块法在内的各种稳态计算方法耦合以求解时空多群中子动力学问题,且取得了很好的计算精度,允许较大的计算时间步长,以及拥有很好的计算效率。
刚性限制法;点堆中子动力学;时空中子动力学;变分节块法
刚性限制法(SCM)是一种中子动力学的时间变量处理方法,最早由美国西屋公司的Chao等[1-2]于20世纪80年代提出。其主要思想是将先驱核浓度控制方程的刚性消除掉,使刚性仅限制在中子密度方程中,而该方程可用解析法求解,从而使整个系统的求解时间步长增大。
刚性限制法的实际应用价值在于快速求解时空中子动力学模型,对于该模型,刚性限制法通过引入动力学频率,将三维多群时空动力学问题转换为三维多群稳态问题,因而缓解动力学问题的“刚性”,使与刚性限制法耦合的稳态程序可在大时间步长下快速计算瞬态变化,并拥有足够的稳定性、准确性和计算效率。
美国西屋公司的赵荣安博士于1984年首次将刚性限制法应用于点堆动力学问题的求解中[1];并于1989年,在西屋公司的压水堆节块程序SUPER-NOVA(SPNOVA)的基础上,开发出了三维动力学计算程序SPNOVA-K[2]。之后,很多学者对此方法进行了研究与发展:2007年日本三菱公司的AOKI等[3]用刚性限制法耦合三维扩散程序ANC得到其动力学版本ANCK,并用ANCK与MIDAC耦合来准确模拟反馈效应;2012年上海核工程研究设计院的司胜义开发了通用的刚性限制法计算程序UASCM[4],可直接与多种稳态扩散或输运程序耦合应用,计算动力学问题。本文基于刚性限制法的主要思想建立计算模型,应用变分节块法(VNM)计算时空中子动力学问题,并对计算效率进行相应优化。
1 刚性限制法的理论模型
瞬发中子动力学频率:
(1)
缓发中子动力学频率:
(2)
其中:n(t) 为时刻t的中子密度,cm-3;Ci(t) 为时刻t的第i组缓发中子先驱核浓度,cm-3。
1.1 点堆中子动力学方程的求解模型
点堆中子动力学方程的一般形式[1]为:
(3)
(4)
其中:Λ为瞬发中子的平均寿命;ρ为当前时刻反应性;λi为第i组缓发中子先驱核衰变常量;βi为第i组缓发中子的份额,β=∑βi。
将式(1)代入式(3),可得:
(5)
将上式代入式(4),并消除中子密度项,可得:
(6)
采用全隐式向后差分方法求解式(6),得到:
(7)
(8)
其中:
(9)
(10)
将求得的缓发中子先驱核浓度代入式(3),得:
(11)
假设在每个时间步长内,缓发中子先驱核浓度不变,用解析法求解该方程:
(12)
将得到的n(tn+1)与Ci(tn+1)代入式(3)计算dn(t)/dt,并更新动力学频率,得:
(13)
重复以上过程直至动力学频率收敛,该时间步计算结束。
1.2 时空中子动力学的求解模型
在笛卡尔坐标系中,分群形式的三维时空扩散中子动力学方程组[1]可描述为:
(14)
(15)
其中:vg为第g群中子的(群)平均速度,cm/s;r=(x,y,z)为空间位置;φg(r,t)为在t时刻r位置处第g群的中子通量密度,cm-2·s-1;Dg(r,t)为第g群的扩散系数;Σt,g(r,t)为第g群中子的总宏观截面,cm-1;χig为第i组缓发中子出现在g群中的概率;χg为裂变中子进入第g群的份额;Σg′-g(r,t)为t时刻r位置处g′群向g群的转移宏观截面,cm-1。
(16)
引入动力学频率,将式(14)和(15)联立,并消去中子通量密度方程中的缓发中子先驱核浓度项:
(17)
将上式化为稳态形式的三维多群中子扩散方程:
χg(1-β)Q′(r,t)+Σg′-g(r,t)φg′(r,t)
(18)
其中:
(19)
(20)
(21)
(22)
利用稳态多群中子扩散计算程序即可求解上述方程组。
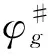
(23)
将其代入式(15),可求得:
(24)
得到系数A后,便可求得中子通量密度的绝对值:
(25)
按照定义更新动力学频率的值:
(26)
类似地,重复以上过程直至动力学频率收敛,该时间步计算结束。
时空刚性限制法通过引入动力学频率,将三维多群时空动力学问题转换成三维多群稳态扩散问题,因而缓解动力学问题的“刚性”,使与刚性限制法耦合的稳态程序可在大时间步长下快速计算瞬态变化。
2 数值结果及其分析
本文应用上述理论模型首先编制了刚性限制法点堆计算程序SCM-Point,并将其嵌入改进准静态计算的点堆方程求解过程中。其次在变分节块法程序Violet的基础上实现其时空动力学版本Violet-K。采用TWIGL Seed Blanket瞬态基准题对上述两个部分分别进行验证,并对计算结果进行分析研究。
TWIGL Seed Blanket瞬态基准题是一个二维两群的瞬态问题。堆芯是一边长为160 cm的正方形,由两种燃料材料组成并分为3个区域,无反射层和反馈。其中,1号区域与2号区域材料相同,1号区域模拟了控制棒插入的情况。问题详细描述参见文献[4]。
该基准题由两组问题组成,分别是燃料区1的热群宏观吸收截面发生阶跃变化和线性变化引起的瞬态过程,初始时刻堆芯相对功率为1.0,瞬态过程计算到0.5 s。
2.1 点堆动力学计算数值结果
选取改进准静态计算过程中0~10 ms的时间段。通量密度以对于初始通量密度的比值即相对通量密度表示。在线性变化和阶跃变化过程,反应性引入量分别为18.48 pcm和383.06 pcm。在此时间段内分别取时间步数1、5、10、50、100、1 000计算时间节点10 ms处的通量密度,采用SCM-Point和隐式差分方法得到的数值计算结果列于表1。
通过与传统的隐式差分方法进行比较后发现,欲达到相同计算精度,刚性限制法可以采用较大的时间步长,本例中刚性限制法的步长可以是隐式差分方法步长的数十倍。数值验证表明,点堆模型中,刚性限制法能够更好地处理方程的刚性,使得在相同的计算精度下,刚性限制法较隐式差分方法收敛更快,可以在保持稳定性的前提下,增大计算时间步长,从而提高计算效率。
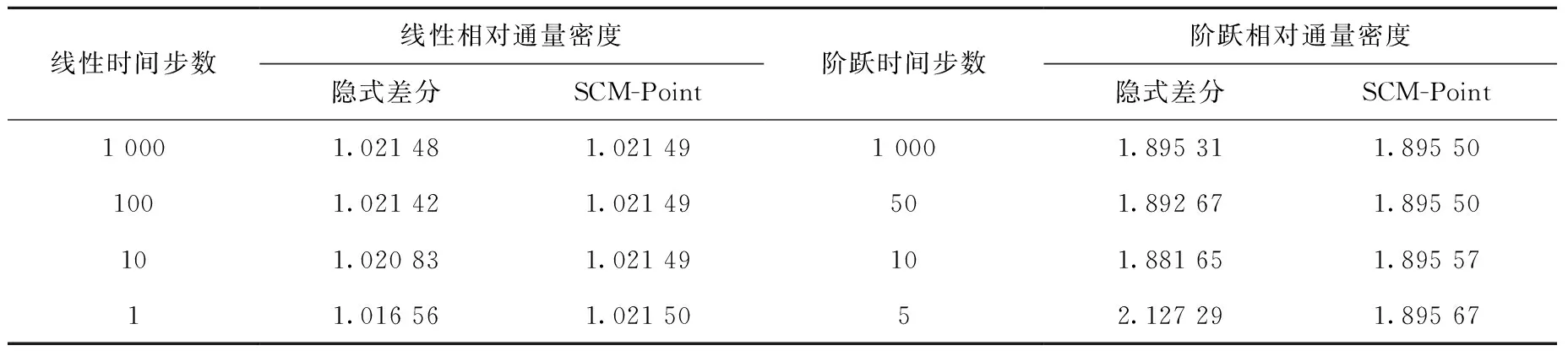
表1 TWIGL Seed Blanket瞬态基准问题10 ms时刻相对通量密度Table 1 Relative flux density of TWIGL Seed Blanket benchmark problem at 10 ms
2.2 时空动力学计算数值结果
使用Violet-K程序选取1/4堆芯进行计算,节块划分为10×10,即x轴方向节块数为10,y轴方向节块数为10。在20 ms和10 ms两种时间步长下计算堆芯相对功率随时间的变化,并列出计算时间,参考解取自文献[5],计算结果列于表2。计算过程中,动力学频率的更新值取前一次迭代与后一次迭代的中间值,外迭代条件取10-6,有效增殖因数收敛条件取10-6,由此得到单步的迭代计算次数约为3次。
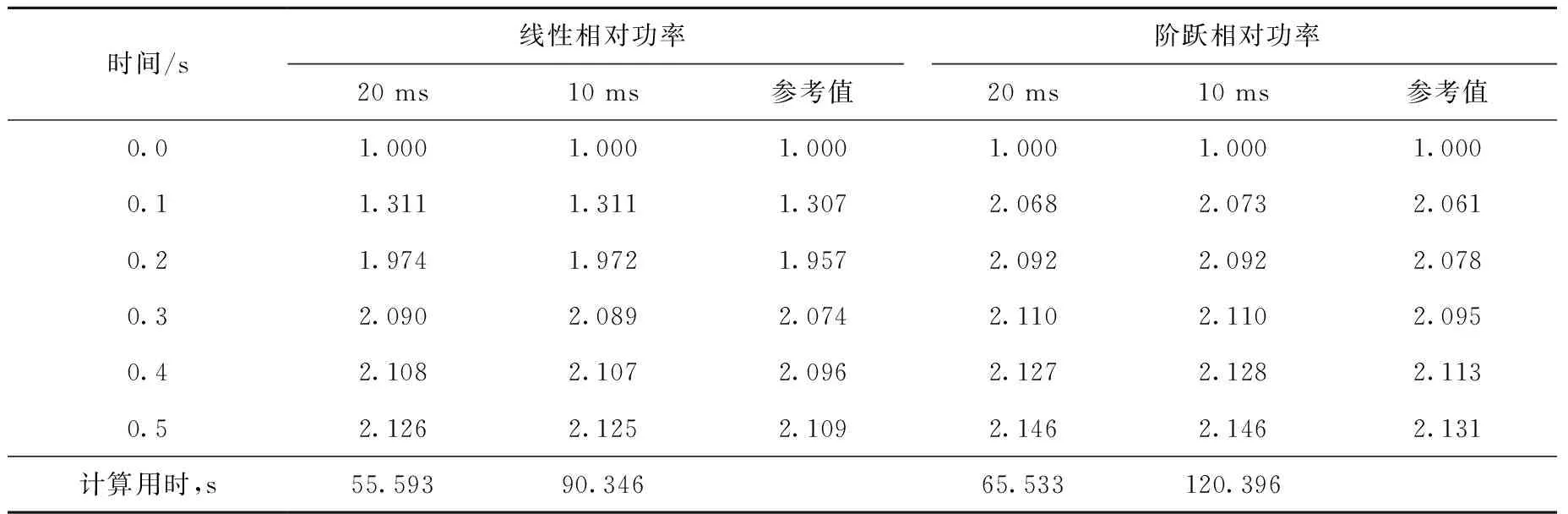
表2 基于Violet-K程序下TWIGL Seed Blanket瞬态基准问题堆芯相对功率随时间的变化Table 2 Variation of core relative power with time in TWIGL Seed Blanket benchmark problem based on Violet-K code
表3列出基于3种稳态程序Violet-K、MGSNM与MGNEM的刚性限制法对于TWIGL Seed Blanket瞬态基准问题的数值结果比较,后两个同类程序数据来源于文献[6]。在相同网格划分条件下,分别对20 ms和10 ms的时间步长,比较3种程序下堆芯相对功率随时间的变化。
数值结果表明,在20 ms和10 ms两种时间步长下,堆芯相对功率的计算结果与参考值均符合得较好,尤其是当步长取20 ms时,仍可保证很好的计算精度,而隐式差分方法对于此问题为保证计算精度通常选取的时间步长为1 ms或2.5 ms。可见时空刚性限制法可较大地增大计算步长,在提高计算效率的同时保证准确率和稳定性。
通过比较基于3种稳态程序下刚性限制法关于堆芯相对功率随时间的变化计算的结果发现,在同类的时空动力学计算程序中,本文所编制的Violet-K程序具有较良好的精度和稳定性,计算结果准确可靠。

表3 基于3种稳态程序下TWIGL Seed Blanket瞬态基准问题堆芯相对功率随时间的变化Table 3 Variation of core relative power with time in TWIGL Seed Blanket benchmark problem based on different codes
3 结论
数值结果验证表明,刚性限制法能更好地处理方程的刚性问题,使得在相同的计算精度下,其可在保持稳定性的前提下,增大计算时间步长,从而提高计算效率。刚性限制法可与包括变分节块法的各种稳态计算方法耦合以求解时空多群中子动力学问题,且取得了很好的计算精度,其允许较大的计算时间步长,拥有很好的计算效率。
[1] CHAO Y, ATTARD A. A resolution of the stiffness problem of reator kinetics[J]. Nuclear Science and Engineering, 1985, 90: 40-46.
[2] CHAO Y, HUANG P. Theory and performance of the fast-running multidimensional pressurized water-reactor kinetics code, SPNOVA-K[J]. Nuclear Science and Engineering, 1989, 103: 415-419.
[3] AOKI S, SUEMURA T, OGAWA J, et al. The verification of 3 dimensional nodal kinetics code ANCK using transient benchmark problems[J]. Journal of Nuclear Science and Technology, 2007, 44(6): 862-868.
[4] SI Shengyi. Algorithm development and verification of UASCM for multi-dimension and multi-group neutron kinetics model[C]∥PHYSOR 2012: Adcances in Reactor Physics-Linking Research, Industry, and Education. USA: [s. n.], 2012.
[5] BANDINI B R. A three-dimensional transient neutronics routine for the TRAC-PF1 reactor thermal hydraulic computer code[D]. Pennsylvania: Pennsylvania State University, 1990.
[6] 吴宏春. 中子扩散方程及其数值方法[M]. 西安:西安交通大学出版社,2005.
Stiffness Confinement Method for Space-time Neutron Kinetics Calculation
WEI Ming-zhe, LI Yun-zhao*, HE Ming-tao
(SchoolofNuclearScienceandTechnology,Xi’anJiaotongUniversity,Xi’an710049,China)
With the improvement of computational ability and the demand for accuracy requirement of neutron kinetics, it has great value in engineering application to deal with the stiffness of three-dimensional space-time neutron diffusion kinetics better. Based on the stiffness confinement method (SCM) and the variational nodal method (VNM), a new combination of neutron kinetics model was developed. It is demonstrated by the numerical results that the SCM can handle the stiffness problem better with larger time step and higher computational efficiency, and be combined with the VNM.
stiffness confinement method; point neutron kinetics; space-time neutron kinetics; variational nodal method
2014-06-29;
2014-08-25
国家自然科学基金资助项目(91226106);长江学者和创新团队发展计划资助项目(IRT1280);上海核工程研究设计院资助项目
魏明哲(1992—),男,辽宁铁岭人,核工程与核技术专业
*通信作者:李云召,E-mail: yunzhao@mail.xjtu.edu.cn
TL329.2
A
1000-6931(2015)10-1828-05
10.7538/yzk.2015.49.10.1828
