遗传算法优化的BP神经网络在EDXRF中对钛铁元素含量的预测

2015-05-04刘明哲庹先国

原子能科学技术 2015年6期

王俊，刘明哲,*，庹先国,2，李哲，李磊，石睿

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都 610059；2.西南科技大学核废物与环境安全国防重点学科实验室，四川绵阳 621010)

王俊1，刘明哲1,*，庹先国1,2，李哲1，李磊1，石睿1

在能量色散X荧光分析(EDXRF)技术中，受均匀效应、颗粒效应和基体效应等的干扰，定量分析精度受到影响。本文针对这一问题提出了遗传算法(GA)优化BP神经网络(GA-BP)的混合算法，该算法无需考虑元素浓度和射线强度之间的复杂关系。遗传算法优化BP神经网络的目的是为了获得更好的网络初始权值和阈值，其基本思想是:将初始化的BP神经网络均方根误差的倒数编码为遗传算法中个体的适应度；初始的权值和阈值用遗传算法中的个体代替，然后通过选择、交叉和变异操作挑选出最优个体，最后通过解码用最优的权值和阈值创建一个新的BP网络模型。攀枝花矿区5类矿样中钛和铁含量的整体预测和分类预测实验表明，分类预测效果远好于整体预测。预测值与化学分析值比较结果表明，其中76.7%的样品相对误差小于2%，表明了该方法在元素间基体效应校正上的有效性。

能量色散X荧光分析；定量分析；BP神经网络；遗传算法

钒钛磁铁矿的成分较复杂，生产过程中要对其进行定量分析。虽然传统的化学分析方法稳定、可靠，但费时费力，且成本较高。能量色散X射线荧光(EDXRF)分析技术是一种先进的非破坏性分析技术，该技术已在水泥、矿业、环境防治等诸多领域中得到了广泛的运用[1-3]。在EDXRF分析技术中，基体效应是影响其分析准确性的一个关键因素，特别是元素间吸收增强效应的干扰，使得荧光强度和元素浓度之间呈非线性关系，在X荧光分析技术领域，基体效应的准确校正仍然是一个难点[4]。传统的实验校正法、数学校正法的准确度在很大程度上依赖于标样的准确度和标样与待测试样的相似性[5]，属于相对测量法。基本参数法克服了相对测量方法的不足，但它所采用的很多基本参数很难确定，如果独立进行测定，参数数据的准确性较差[6]。Guo等[7-9]将遗传算法、神经网络等运用于XRF、EDXRF和PIXE的微区定量分析中，取得了较好的成果。宋梅村和李金阳等[10-11]将BP神经网络方法用于核反应堆的功率预测和核电厂主动容错控制方法的研究中，均证明BP神经网络具有很好的非线性过程逼近能力。

在存在强吸收增强效应的复杂矿样中，如何得到更精确的分析结果，一直以来都是X射线荧光分析技术研究者努力想要解决的问题。本文提出利用遗传算法(GA)优化BP神经网络的权值和阈值的混合算法，来校正元素间的基体效应，该方法无需考虑荧光强度和元素浓度间的复杂关系，直接从训练样本的浓度、强度数据中抽取它们的相关关系用于元素含量的定量分析。

1 方法研究

GA-BP网络模型有3层：m个节点的输入层、h个节点的隐含层和n个节点的输出层。首先，模型给出1个基本状态空间的连接权值矩阵；然后，将隐含层节点和权值矩阵通过编码形成包含整数和真实值的字符串；最后通过解码再重新建立1个新的BP网络[12]。该方法的执行步骤如下：

第1步：建立1个具有3层结构的BP神经网络，训练出1个在[-1,1]范围内的连接权值和阈值矩阵，用于GA优化。

第2步：连接权值和隐含层节点编码，隐藏的节点编码为二进制代码字符串，1代表输入和输出层节点之间有连接，0则代表无连接；连接权值编码为浮点字符串，串长H=m×h+h+h×n+n。每个字符串对应1个包含某些基因片段的染色体，染色体的编码由A、B、C、D、E5个部分组成。其中，A为隐含层节点；B为输入层到隐含层权值；C为隐含层阈值；D为隐含层到输出层权值；E为输出层阈值。A部分是0和1组成的二进制码；B、C、D、E为0.1～0.9之间的真实值，这些值在训练中将会发生改变。

第3步：由染色体组成的种群初始化，每个染色体的长度L为G+H，G为隐含层节点二进制码的长度。

第4步：适应度函数计算。计算公式如下：

(1)

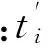
第5步：按式(2)计算种群中所有个体的适应度之和，以及每个个体的相对适应度，并以此作为遗传到下一代的概率，具有最高相对适应度的个体直接复制到下一代，剩下的采用轮盘赌的方式遗传到下一代。

(2)

第6步：使用基本的交叉和变异操作来控制代码,即,如果一个隐藏节点被删除(或添加),根据突变操作,相应的控制代码编码是0(或1)，交叉和变异算子的权值编码如下。

1) 给定概率Pc的交叉操作：

(3)

(4)

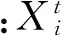
2) 给定概率Pm的变异操作：

(5)

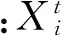
第7步：重复第4～6步，直至满足收敛条件，用产生的新种群代替当前种群。

第8步：解码适应度最大的个体获得相应的连接权值和阈值，建立新的BP网络并输出预测结果。

2 实验设计

实验样品采用来自攀枝花矿区的5类矿样：原矿、铁精矿、铁尾矿、钛精矿、钛尾矿，各取4 kg，粉碎后在105～110 ℃下烘干1 h，减小湿度效应的影响。测量前，取少许在玛瑙研钵中研磨30 min，保证均匀性；过180目筛子，降低颗粒效应的不利影响。实验采用CIT-3000SM型EDXRF分析仪，X光管激发、电制冷半导体Si(PIN)探测器，能量分辨率为180～190 eV(55Fe，5.90 keV)。实验时，管压12.25 kV，管流25.68 μA，环境温度25 ℃。用粉末压片法制样，每组样品测量3次，每次测量3 min，取3次测量结果对应道址的平均计数率作为最终的分析数据。图1为待测样品，图2为铁精矿中含54.45%铁和7.0%钛样品的EDXRF能谱。

图1 待测样品Fig.1 Sample to be tested

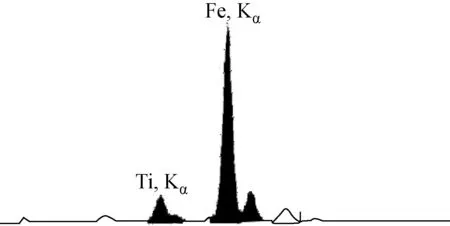
图2 钛、铁EDXRF能谱Fig.2 EDXRF spectra of titanium and iron

5类矿产样品中均含有10多种元素(Ca、V、Cr、Ni、Cu、Zn、As、Pb、Ti和Fe等)，但钛和铁是其中最主要的组成元素。用能量谱对其进行标定后，选择4.038～8.364 keV (280～580道)之间的能谱数据作为研究对象，因为在该能量区间包含了影响钛和铁含量定量分析的主要元素Ti、Fe、V、Ni和Cu，它们的特征X射线Kα能量分别为：Ti，4.510 keV；Fe，6.403 keV；V，4.951 keV；Ni，7.477 keV；Cu，8.046 keV。

实验样品是钛和铁含量均不相同的5类矿样，每类16组，共80组。实验分2组进行，第1组实验为5类矿样分别训练和预测，其中每类矿样中10组作为训练样本，6组作为预测样本，实验分5次进行；第2组实验为5类矿样整体训练和预测，即将第1组实验中的50组训练样本和30组预测样本分别作为整体训练和预测的样本，实验一次完成。各样品中钛和铁的浓度通过化学分析方法获得，化学分析值作为实验的期望输出值。2组实验分别进行30次，分别统计钛和铁含量的预测值。采用相对误差与变异系数判断两组实验结果的准确度与精确度。

在GA-BP网络结构中，取能量区间4.038～8.364 keV内每道址所对应的计数率为输入变量，共301个神经元；钛和铁的含量作为输出层的输出变量，共2个神经元；输入层到隐含层的激发函数选择logsig函数，隐含层到输出层的激发函数选择purelin函数，网络训练函数选择traincgb函数。GA-BP网络结构的各项重要参数列于表1。

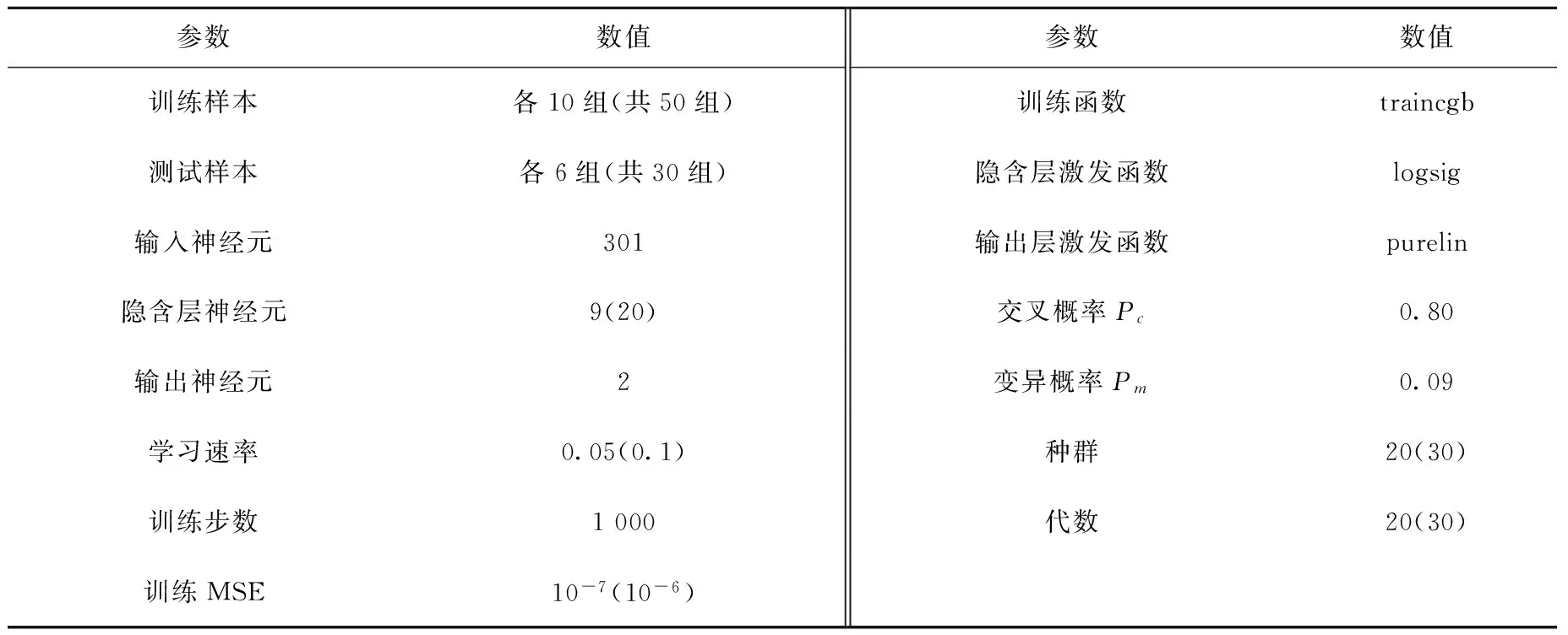
表1 各项网络模型的重要参数Table 1 Important parameters for required model

注：括号内为整体预测实验参数，括号外为分类预测实验参数

3 实验结果与分析

分类预测和整体预测中训练网络收敛到均方根误差(MSE)和适应度的情况列于表2。从表2可看出：分类预测收敛步数远小于整体预测的，收敛速度要快于整体预测的，这是因为整体预测数据量大于分类预测数据量；适应度二者相当。

整体预测和分类预测中训练网络的MSE和适应度收敛的过程分别示于图3、4。由图3、4可见，整体预测和分类预测的MSE收敛过程中的预设目标值均达到了最佳值，所以预设目标值与最佳值曲线重合；从MSE与适应度收敛过程来看，在遗传算法优化过程中，两组实验均未出现局部最小值点，说明经过GA优化后的BP神经网络不易陷入局部最小值点。

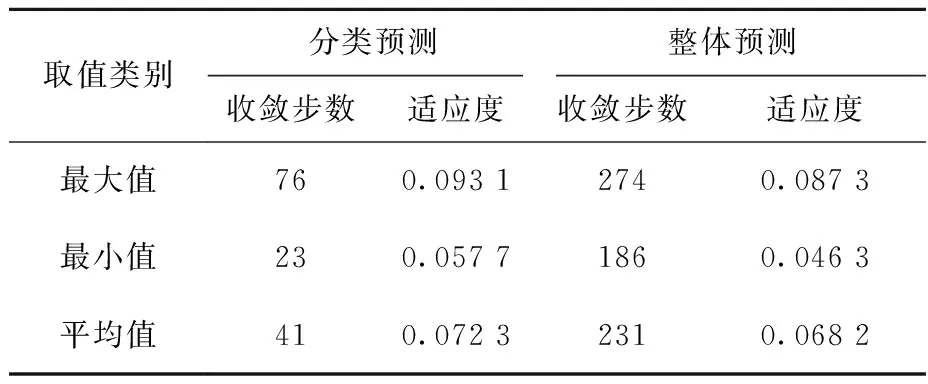
表2 收敛步数与适应度Table 2 Steps of convergence and fitness value

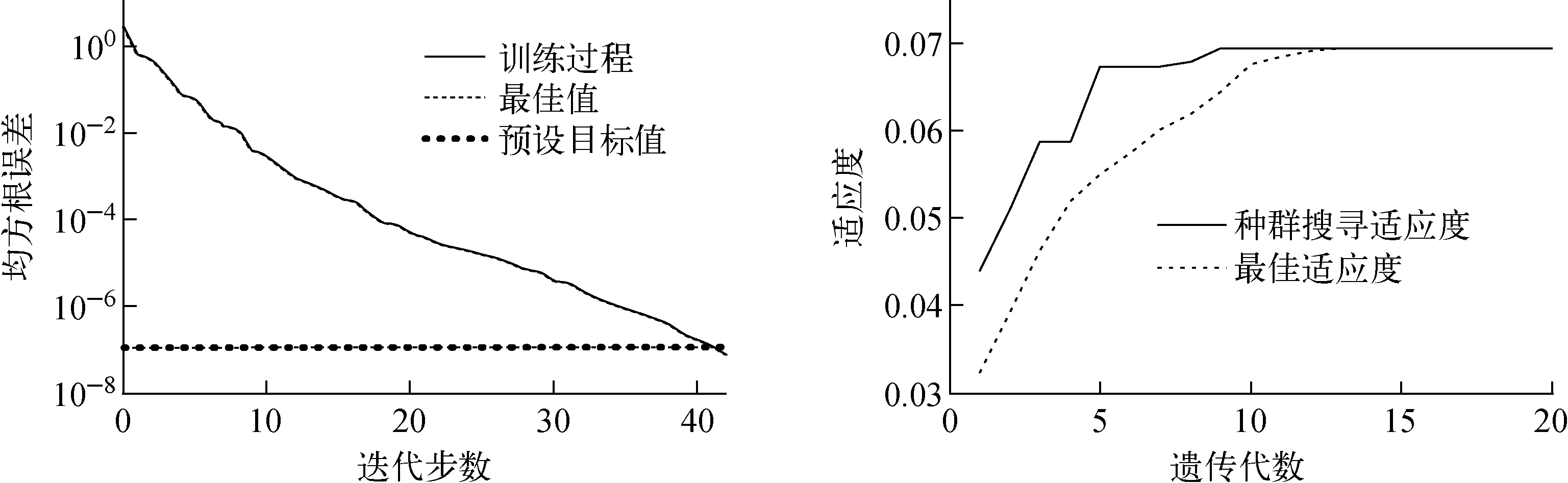
图4 分类预测的收敛均方根误差曲线与适应度曲线Fig.4 Convergence curve of MSE and fitness value for classification prediction

整体预测和分类预测实验结果与化学分析值的比较分别示于图5、6，图中，从左起分别为原矿、钛尾矿、钛精矿、铁精矿、铁尾矿。由图5、6可见，虽然实验结果与化学分析值符合较好，但整体预测时，数据离散度远大于分类预测，分类预测结果要好于整体预测，说明数据离散度是影响GA-BP方法的一个重要因素。

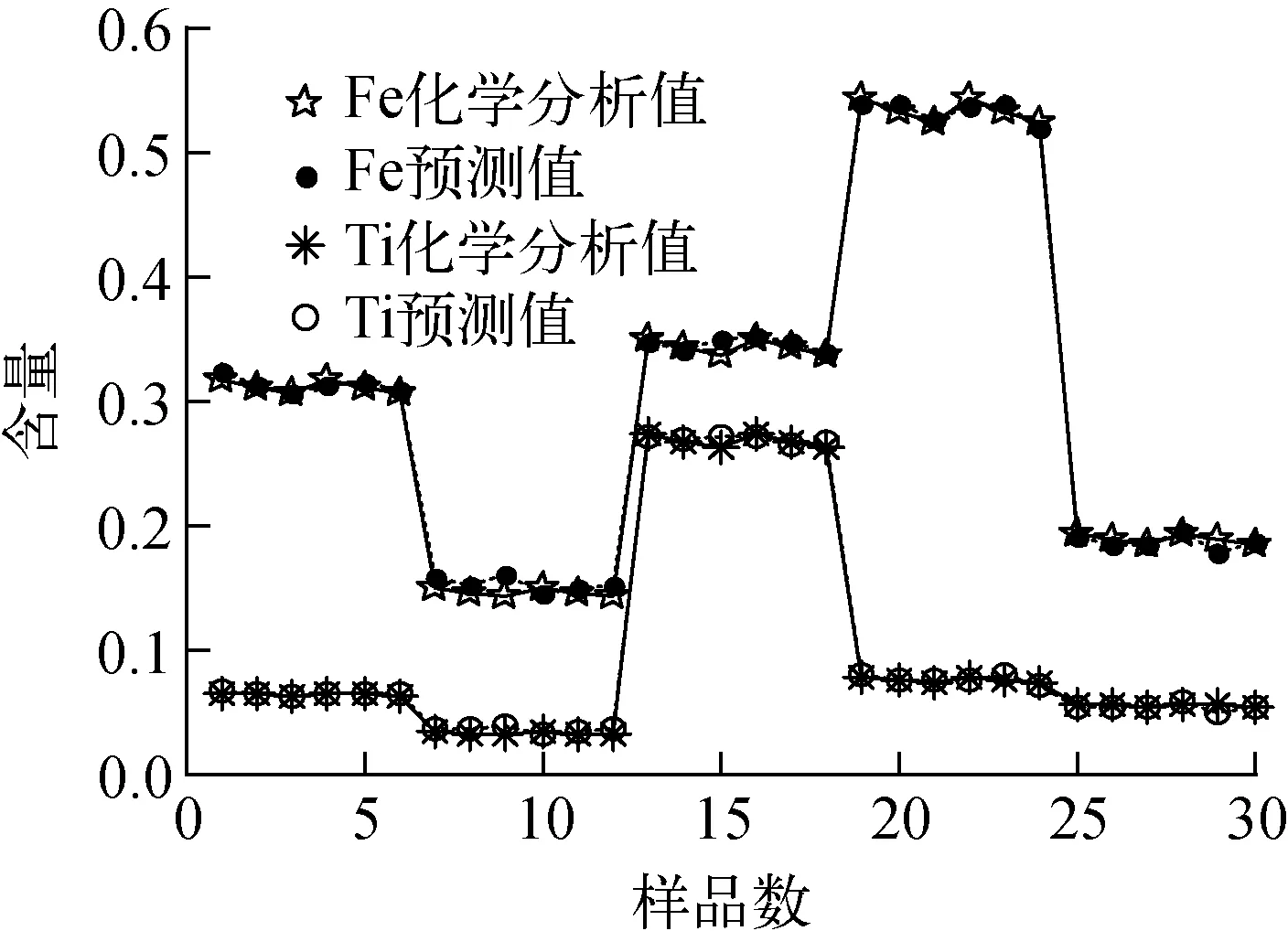
图5 整体预测值与化学分析值Fig.5 Overall predicted values and chemical analysis values

图6 分类预测值与化学分析值Fig.6 Classification predicted values and chemical analysis values

分类预测和整体预测结果的准确度和精确度即相对误差和变异系数列于表3。由表3可看出，两类实验结果平均相对误差均小于5%，但分类预测的准确度和精确度均明显好于整体预测，分析其原因在于，矿样分类后，分析数据间的离散度大幅减小，这将有利于GA优化后的BP神经网络得到更好的权值和阈值，进而获得更佳的实验结果。

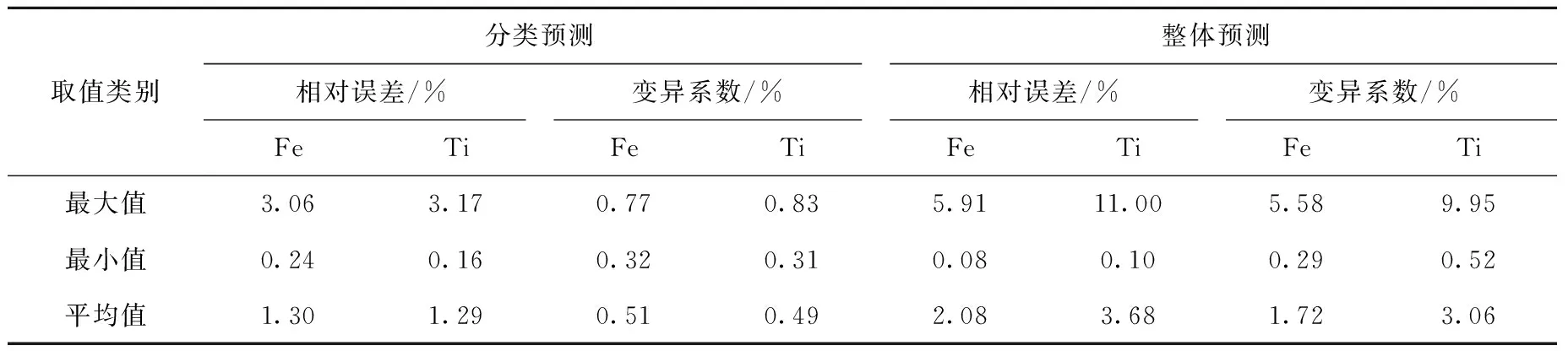
表3 分类预测和整体预测的准确度和精确度Table 3 Accuracy and precision of classification prediction and overall prediction

4 结论

本文提出了一种新的基于GA-BP的混合算法用于X射线荧光能谱数据的处理。经过优化的BP神经网络收敛速度快且不易陷入局部最小值点。该方法在分析成分复杂的钒钛磁铁矿时，无须考虑元素浓度与荧光强度之间的复杂关系，而是直接从训练样本中提取相关信息，对主要元素铁和钛的含量进行分析。实验结果表明，分类预测平均相对误差小于2%，整体预测平均相对误差小于4%；分类预测精度要好于整体预测。该方法没有受到强的基体效应的影响。

值得注意的是，将复杂的矿样分类，其实质是减小了训练样本与预测样本的差异性，这样处理有利于获得更优的BP神经网络的权值和阈值，进而能获得更好的实验结果。

[1] SUMPUN W, PHADOONG B, THIPPAWAN S. Determination of impurities in ilmenite ore and residues after leaching with HCl-ethylene glycol by energy dispersive X-ray fluorescence (EDXRF) spectrometry[J]. Hydrometallurgy, 1997, 45(1-2): 161-167.

[2] GONZALEZ-FERNANDEZ O, QUERALT I, CARVALHO M L, et al. Elemental analysis of mining wastes by energy dispersive X-ray fluorescence (EDXRF)[J]. Nuclear Instruments and Methods in Physics Research B, 2007, 262(1): 81-86.

[3] NATARAJAN V, PORWAL N K, BABU Y, et al. Direct determination of metallic impurities in graphite by EDXRF[J]. Applied Radiation and Isotopes, 2010, 68(6): 1 128-1 131.

[4] RICHARD M R. Corrections for matrix effects in X-ray fluorescence analysis: A tutorial[J]. Spectrochimica: Acta Part B, 2006, 61(7): 759-777.

[5] 曹利国. X射线荧光分析中的综合灵敏度因子KI0和准绝对测量[J]. 核技术,1987,10(7)：15-21.

CAO Liguo. Comprehensive sensitivity factor KI0and quasi-absolute determination in XRF[J]. Nuclear Techniques, 1987, 10(7): 15-21(in Chinese).

[6] 曹利国,丁益民,黄志琦. 能量色散X荧光方法[M]. 成都:成都科技大学出版社,1998:182-274.

[7] GUO P L, WANG J Q, LI X J, et al. Combination of pattern recognition with micro-PIXE for the source indentification individual aerosol particles[J]. Applied Specscopy, 2000, 54(6): 807-811.

[8] LUO L Q. An algorithm combining neural networks with fundamental parameters[J]. X-Ray Spectrometry, 2002, 31(4): 332-338.

[9] 李哲,庹先国,穆克亮,等. 矿样中钛铁EDXRF分析的基体效应和神经网络校正研究[J]. 核技术,2009,32(1)：35-40.

LI Zhe, TUO Xianguo, MU Keliang, et al. Matrix effect and ANN correcting technique in EDXRF analysis of Ti and Fe in core samples[J]. Nuclear Techniques, 2009, 32(1): 35-40(in Chinese).

[10]宋梅村，蔡琦. 基于BP神经网络的反应堆功率预测[J]. 原子能科学技术,2011,45(10):1 242-1 246.

SONG Meicun, CAI Qi. Reactor power prediction based on BP neural network[J]. Atomic Energy Science and Technology, 2011, 45(10): 1 242-1 246(in Chinese).

[11]李金阳,夏虹,刘永阔,等. 基于BP神经网络的核电厂主动容错控制方法研究[J]. 原子能科学技术,2012,46(7):827-830.

LI Jinyang, XIA Hong, LIU Yongkuo, et al. Active fault tolerant control research for nuclear power plant based on BP neural network[J]. Atomic Energy Science and Technology, 2012, 46(7): 827-830(in Chinese).

[12]OZKAYA B, DEMI A, BILGILI M S. Neural network prediction model for the methane fraction in biogas from field-scale landfill bioreactors[J]. Environmental Modeling & Software, 2007, 22(6): 815-822.

BP Neural Network Optimized by Genetic Algorithm Approach for Titanium and Iron Content Prediction in EDXRF

WANG Jun1, LIU Ming-zhe1,*, TUO Xian-guo1,2, LI Zhe1, LI Lei1, SHI Rui1

(1.StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,China； 2.FundamentalScienceonNuclearWastesandEnvironmentalSafetyLaboratory,SouthwestUniversityofScienceandTechnology,Mianyang621010,China)

The quantitative elemental content analysis is difficult due to the uniform effect, particle effect and the element matrix effect, etc, when using energy dispersive X-ray fluorescence (EDXRF) technique. In this paper, a hybrid approach of genetic algorithm (GA) and back propagation (BP) neural network was proposed without considering the complex relationship between the concentration and intensity. The aim of GA optimized BP was to get better network initial weights and thresholds. The basic idea was that the reciprocal of the mean square error of the initialization BP neural network was set as the fitness value of the individual in GA, and the initial weights and thresholds were replaced by individuals, and then the optimal individual was sought by selection, crossover and mutation operations, finally a new BP neural network model was created with the optimal initial weights and thresholds. The calculation results of quantitative analysis of titanium and iron contents for five types of ore bodies in Panzhihua Mine show that the results of classification prediction are far better than that of overall forecasting, and relative errors of 76.7% samples are less than 2% compared with chemical analysis values, which demonstrates the effectiveness of the proposed method.

EDXRF; quantitative analysis; BP neural network; genetic algorithm

2014-02-18;

2014-05-03

国家杰出青年科学基金资助项目(41025015)；国家自然科学基金资助项目(41274109)；四川省青年科技创新研究团队资助项目(2011JTD001)；四川省科技支撑计划资助项目(2013FZ0022)

王俊(1984—)，男，四川西昌人，硕士研究生，核能与核技术工程专业

*通信作者：刘明哲，E-mail: liumz@cdut.edu.cn

TL99

1000-6931(2015)06-1143-06

10.7538/yzk.2015.49.06.1143