高温气冷堆环境模拟装置动态传热特性建模分析
2015-05-04李聪新杨星团姜胜耀孙艳飞
李聪新,任 成,杨星团,姜胜耀,孙艳飞
(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室,北京 100084)
高温气冷堆环境模拟装置动态传热特性建模分析
李聪新,任 成,杨星团*,姜胜耀,孙艳飞
(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室,北京 100084)
清华大学核能与新能源技术研究院研制了模拟高温气冷堆温度、环境氛围的材料测试装置,可进行1 600 ℃及以下高温碳还原环境下的各类实验。通过对该实验装置的结构进行适当简化,建立了模拟其高温、真空条件下辐射、导热动态传热特性的二维数学模型。仿真结果与实验装置各测点的实测温度变化趋势一致,可解释实验时观察到的多种动态传热现象。此外,该模型可对材料测试区径向温度分布、不同加热功率条件下发热体最高温度等难以直接测量的重要参数进行估计,给出进一步实验的指导性建议。
高温气冷堆;环境模拟装置;高温;真空;辐射传热
大型先进压水堆及高温气冷堆核电站项目被列入《国家中长期科学和技术发展规划纲要》16个重大专项之一,发展高温气冷堆技术是一项重大的国家战略[1],不但关系到国家能源安全,而且对于带动相关产业的发展具有重要意义,尤其是相关材料产业的发展,具有十分广阔的前景。
目前,与高温气冷堆技术配套的工业体系尚未完全建立。虽然我国在重大设备制造方面已有突破,但在材料相关配套工业方面还有待进一步发展。国内针对高温气冷堆环境下的材料测试与考验方面的研究不多,设计计算主要参考国外的材料数据[2],因此很多材料依赖进口,价格昂贵。事实上,目前国内工业界在高温材料研发、制造方面发展迅速,新材料、新工艺层出不穷,但是否能在高温气冷堆环境氛围下应用却尚不清楚。
为此,清华大学核能与新能源技术研究院研制了模拟高温气冷堆温度、环境氛围的材料实验装置,该装置可进行1 600 ℃及以下高温、真空、碳还原环境下的实验,开展相关材料的研究工作[3]。目前,该实验装置已取得一系列1 600 ℃左右的实验数据[4-5]。由于目前测量方法和工程因素的限制,实验装置的部分关键参数(如发热体动态温度)难以直接测量,高温动态实验过程缺乏定性指导,因此,有必要建立该实验装置在高温、真空条件下的动态辐射导热模型,进一步深入理解实验过程中的传热现象,指导后续实验进行。
1 实验装置
1.1 高温气冷堆环境模拟装置
该装置设计为石墨电阻炉形式,中心采用电极石墨做发热体,该发热体是圆柱形电极石墨通过切削而成。石墨发热体外侧为石墨均温套筒,在真空条件下,两者之间的热传递方式仅有表面对表面辐射。均温套筒外侧为环形材料测试区,在本次实验过程中其为直径60 mm石墨球(约700个)组成的随机堆积球床。材料测试区外是硬质碳毡保温层。中心区域高度为1 m,上面是500 mm厚软质碳毡保温层和200 mm厚真空腔,下面是500 mm厚硬质碳毡保温层。铜电极和石墨电极穿过下保温层连接到发热体。保温层外侧为双层水冷壁,在真空实验条件下可保持炉内压力小于30 Pa。材料测试区和上、下、侧保温层均布置有测温热电偶。测试装置的内部结构、材料、测点位置示于图1。
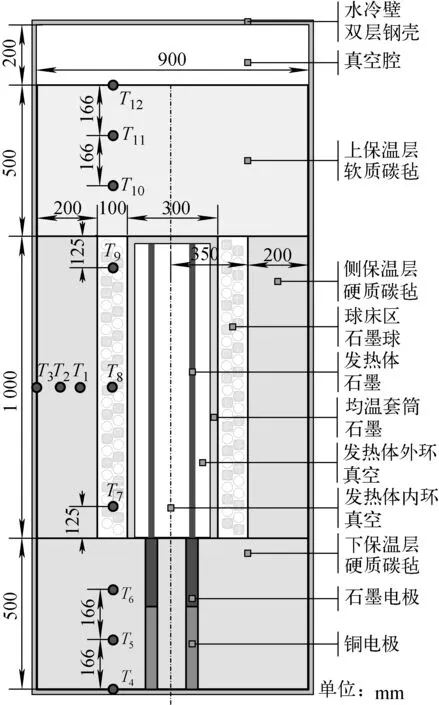
图1 环境模拟装置内部结构、材料和测点布置Fig.1 Inner structure, materials and arrangement of test points of environment simulating facility
在动态仿真过程中所需材料物性参数参考值列于表1。

表1 材料热物性参数参考值Table 1 Reference value of material thermal property
1.2 实验过程
本次模拟的对象是一次已完成的钨铼热电偶在1 600 ℃高温、真空条件下与石墨球直接接触的稳定性考验实验。该实验过程持续时间较长,选取其中调节功率升温、1 100 ℃左右保温、再升温到1 600 ℃左右保温的一个过程作为模拟仿真的对比数据。该过程约60 h,动态过程中功率调节如图2所示。

图2 实验过程中的加热功率Fig.2 Heating power during experiment process
实验过程中球床及保温层中实测温度变化如图3所示。其中T1~T12为测量装置对应位置测点的温度。

图3 球床及保温层温度历史Fig.3 Temperature history of pebble bed and insulation layer
2 数学模型
实际实验装置的三维结构复杂,难以建立完全反映其具体结构和物理过程的仿真模型。除均温套筒、保温层等简单结构、单一材料区域可直接应用柱坐标系下的二维导热方程外,其他结构须经适当简化,才能进行动态模拟仿真。
2.1 发热体
石墨发热体的三维结构如图4所示,发热体主体为环状,侧面挖有凹槽,下面与石墨电极相连。将其简化为一具有内热源的圆环,圆环表面为真空条件下的表面对表面辐射。

图4 石墨发热体三维模型Fig.4 3D model of graphite heater
对于发热体内部,有:
(1)
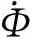
(2)
其中:P为总加热功率,根据加热回路各部分的电阻计算结果,发热体发热量约为总加热功率的95%;V为发热体实际体积。等效圆环的内半径、高度和体积分别与原发热体相同,从而保证质量守恒。
假设圆环内外表面为灰体表面,根据所用石墨材料表面发射率,圆环表面发射率ε取为0.9,则:
(3)
其中:∂T/∂n为表面外法线方向温度梯度;Eb为当前温度下的黑体辐射,Eb=n2σT4,σ为斯特潘-波尔兹曼常量;n为透明介质的折射率,在真空中为1;J为圆环表面的有效辐射;(1-ε)/ε为单位表面积的表面辐射热阻。
2.2 球床
球床区由约700个直径60 mm的石墨球随机堆积而成,其三维结构如图5所示。球床区域宽100 mm,约为2倍球径。球床导热机理复杂,在真空条件下有3种传递方式[6]:1) 均温套筒、石墨球、侧保温层内侧三者的表面间相互辐射;2) 均温套筒、石墨球、侧保温层的接触导热;3) 石墨球内部的导热。3种热传导方式存在耦合关系,不能忽略某种传热方式,必须进行适当简化才能进行计算。
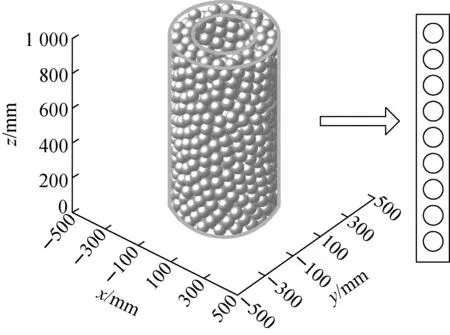
图5 球床和等效结构Fig.5 Pebble bed and equivalent structure
球床传热通常采用等效导热系数计算,将球床视为一拟均匀介质,其导热系数是辐射、导热、对流等作用的总体效果。目前有多种等效导热系数的经验公式[7],但都不适用距壁面4倍球径以内的近壁面区域[8],因此本实验装置的球床区不能采用等效导热系数计算。
随着计算机能力的增强和CFD软件的发展,目前已可对规则堆积的球床流动、传热进行直接数值模拟[9-12],但以目前的计算能力,直接数值计算仅限于球床中的局部结构,球的个数一般为一到几十个,当计算中涉及球表面间辐射传热时,可直接进行三维数值模拟的球的个数更少,即使采用多面体网格等高效率的CFD方法[13],也难以对由700多个球随机堆积的结构进行直接计算。
在高温、真空条件下,球床动态传热特性主要由球内部的导热和球表面对空间辐射的遮挡决定,为此,将球床区简化为柱坐标下一排竖直排列的圆,这些圆和侧壁以及圆和圆之间等间距排列、并不直接接触。
由于球是一个三维结构,若这些圆绕对称轴旋转所形成的圆环体积等于真实球床的球总体积,则总的遮挡面积将减少,因此在模拟时圆面积适当增大,旋转圆环体积大于真实球床体积。为保证质量守恒,密度做相应减小,从而保证球床总热容不变,导热系数保持不变,从而保证稳态传热量不变。
因为接触面积非常小,欲模拟直接接触会导致计算网格数目极大增加,多数文献[12-13]在进行球床局部结构直接计算时也采用不接触的结构。接触导热通过在圆的间隙中填充一热容很小的不参与辐射的导热介质计算,作为不考虑球接触导热的一种修正。适当调整填充介质的导热系数以使模拟结果和真实测量结果更接近。
无论是对于圆还是填充介质内部,均可用相同的导热方程形式描述:
(4)
其中,ρi、ci和λi分别为石墨或虚拟填充介质的密度、比热容和导热系数。
对于交界面,由交界面两侧热流量守恒得:
(5)
其中:λ1为石墨球的导热系数;λ2为填充介质的导热系数。
2.3 电极
电极由石墨电极和铜电极两部分通过螺纹连接而成,如图6所示。石墨电极上部通过石墨螺栓和发热体相连。电极外面是绝缘套筒,用于和下保温层碳毡绝缘。电极和绝缘套筒以及绝缘套筒和下保温层之间均存在间隙。
将电极和绝缘套筒等效为柱坐标下同体积矩形区域导热,由于铜的电阻率远小于石墨,可认为铜电极不含内热源,石墨电极内热源为总加热功率的5%。绝缘套筒及间隙结构用薄热阻层近似,石墨电极与铜电极、石墨电极与发热体连接处的热阻也通过薄热阻层近似。假设薄热阻层会使两种介质交界面处温度不连续,且两界面温度分别为T1和T2,则:
(6)
其中:λ1、λ2为两种介质的导热系数;λs为假设薄热阻材料的导热系数,通常是一个小值;ds为假设薄热阻层的厚度。

图6 电极及等效结构Fig.6 Electrode and equivalent structure
2.4 水冷壁
炉体外壁和上下端盖均为中间通有冷却水的双层钢结构。将其简化为等厚度钢板,外部处于水强制对流的第3类边界条件:
(7)
其中,表面传热系数h取值为1 000~1 500 W/(m·K)。
2.5 简化结果
实验装置简化后的结果与图1类似,为柱坐标系下二维轴对称结构。用于求解的网格和主要传热方式如图7所示。发热体、碳毡、电极等矩形区域采用四边形结构化网格;球床简化成的圆及其间隙采用三角形网格(为了清晰,间隙网格作了隐藏处理);真空区域为表面对表面传热,不需离散网格。
3 计算结果分析
上述仿真模型采用COMSOL Multiphysics软件求解,所有计算结果均为网格无关解,因此不再进行网格无关性讨论。

图7 传热方式与离散网格Fig.7 Heat transfer mechanism and discrete mesh
首先采用实验过程中真实加热功率做发热体和石墨电极内热源计算模型动态过程,验证模型可行性;然后通过该模型计算特定实验条件下的动态过程,获得难以直接测量的实验参数,指导后继实验进行。
3.1 实验验证
用实际实验功率作为仿真过程中发热体和石墨电极内热源强度计算得到的各测点的温度趋势如图8所示。与图3相比,计算结果与实验结果在整体变化趋势上基本一致,但在部分具体数值上不完全吻合。

图8 计算得到的温度历史曲线Fig.8 Curve of calculated temperature history
1) 球床区
实验过程中以球床区测点温度作为调节加热功率的参考,保证温度以恒定速率上升,并进行一段时间的保温,图8的仿真结果可清晰地反映这一动态过程,温度均经历了两次线性上升和保持过程,与实际实验情况一致,可见计算模型符合实验装置的主要导热机理。在高温保温阶段,计算和模拟结果较为一致,均为1 600 ℃左右,但在中段1 100 ℃保温阶段,计算得到的结果约为900 ℃,约有20%的误差。考虑到碳毡材料物性参数参考值的误差和各部分真实结构的简化,计算结果绝对值的误差可接受。
球床区中心布置的3只测温热电偶,虽然轴向为对称布置,但由于下保温层导热系数较上保温层导热系数大,加之电极结构引起的热量散失,导致球床区温度分布并非沿轴向中心对称,从实验结果(图3)可见,上、中两个测点(T8、T9)温度接近,与下面测点(T7)有一定温差,从图8也可看出这一现象。
2) 保温层
由于保温层材料、厚度不同,热量从中心发热体传递到保温层测点的传热机理也不同,在加热的动态过程中,各测点对于加热功率变化的动态响应不同,会观察到保温层温度历史曲线存在复杂的交叉现象。数值模拟的结果也充分显示了这种现象,以侧保温层内侧温度T1和上保温层下侧温度T10为例,测量和计算温度都表现出多次交叉现象。这是由于热量主要以导热方式传递到上保温层测点,温度对导热系数影响不大;而热量传递到侧保温层则要通过1个纯辐射层和1个辐射导热都存在的球床层,之后才通过导热方式在侧保温层传输。辐射传热与绝对温度的4次方成正比,因此在不同温度下,径向导热性能不同,在功率变化时,动态特性更加复杂。
3.2 实验指导
通过对比实验和仿真结果可知,尽管由于装置本身结构的复杂性,材料物性参数、边界条件的不确定性及对随机球床等部分的简化,仿真结果与实测结果在部分绝对数值上有一定的偏差,但构建的二维模型基本上包含了材料测试装置在真空条件下辐射、导热的主要物理规律,仿真结果与实验结果在整体变化趋势上基本一致,可给出特定实验现象的合理解释。
除了对实验现象进行解释,该模型的另一个重要作用是对后续实验进行预测和指导。实验中只能测量该装置少数代表性测点位置的温度,仿真模型可计算出实验装置的整体温度场分布,如1 600 ℃保温阶段,装置内部温度分布如图9所示,可见,材料测试区和发热体温度较为均匀,主要温降在保温层区域;球床区域对应的侧保温层轴向温度变化很小,可近似为径向一维导热。

图9 1 600 ℃时稳态温度场分布Fig.9 Static temperature distribution at 1 600 ℃
1) 径向温降
材料测试装置设计的基本要求之一是环形球床测试区域温度均匀,但由于从中心区域到球床径向只有一个测点,难以检验径向温度分布。从仿真结果(图10)可看出,在1 600 ℃时,径向温降主要在侧保温层,球床区域可近似认为温度均匀。
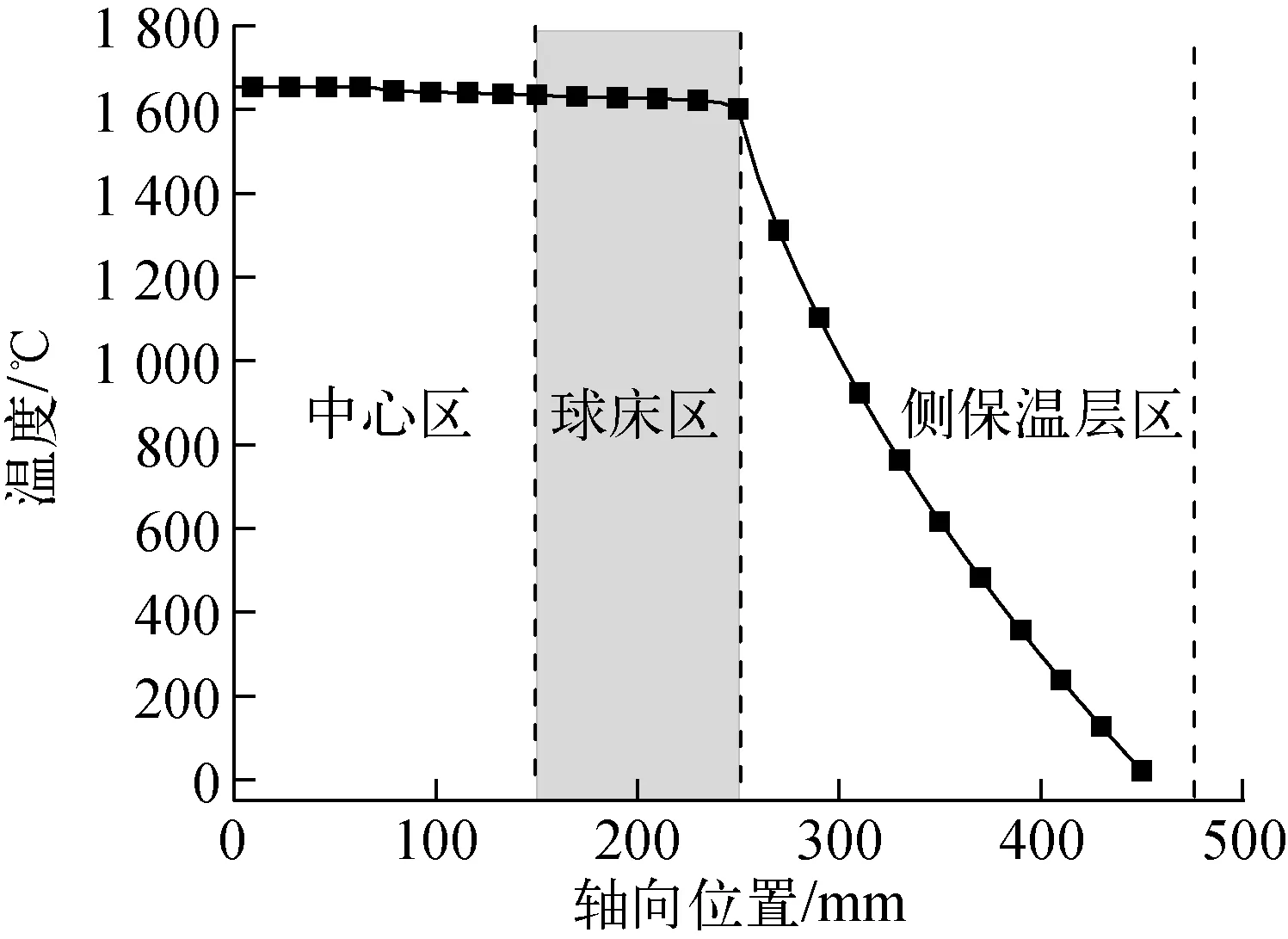
图10 径向温度分布Fig.10 Radial temperature distribution
2) 发热体过热温度
发热体内部由于通电等原因,无直接温度测点。在升温过程中,以球床区测点温度作为升温参考,必须保证发热体不因温度过高而损坏。由于在动态过程中发热体温度与球床温度的差值不确定,加热方案采用保守设定,开始采用小功率加热,并随温度升高逐步增加功率。从实际加热功率的仿真结果看,发热体温度始终未超过2 000 ℃,不会因超温而损坏。但在加热开始的阶段,发热体温度较球床温度高,最高时超过球床温度300 ℃,其差值随温度整体升高而减小,如图11所示。
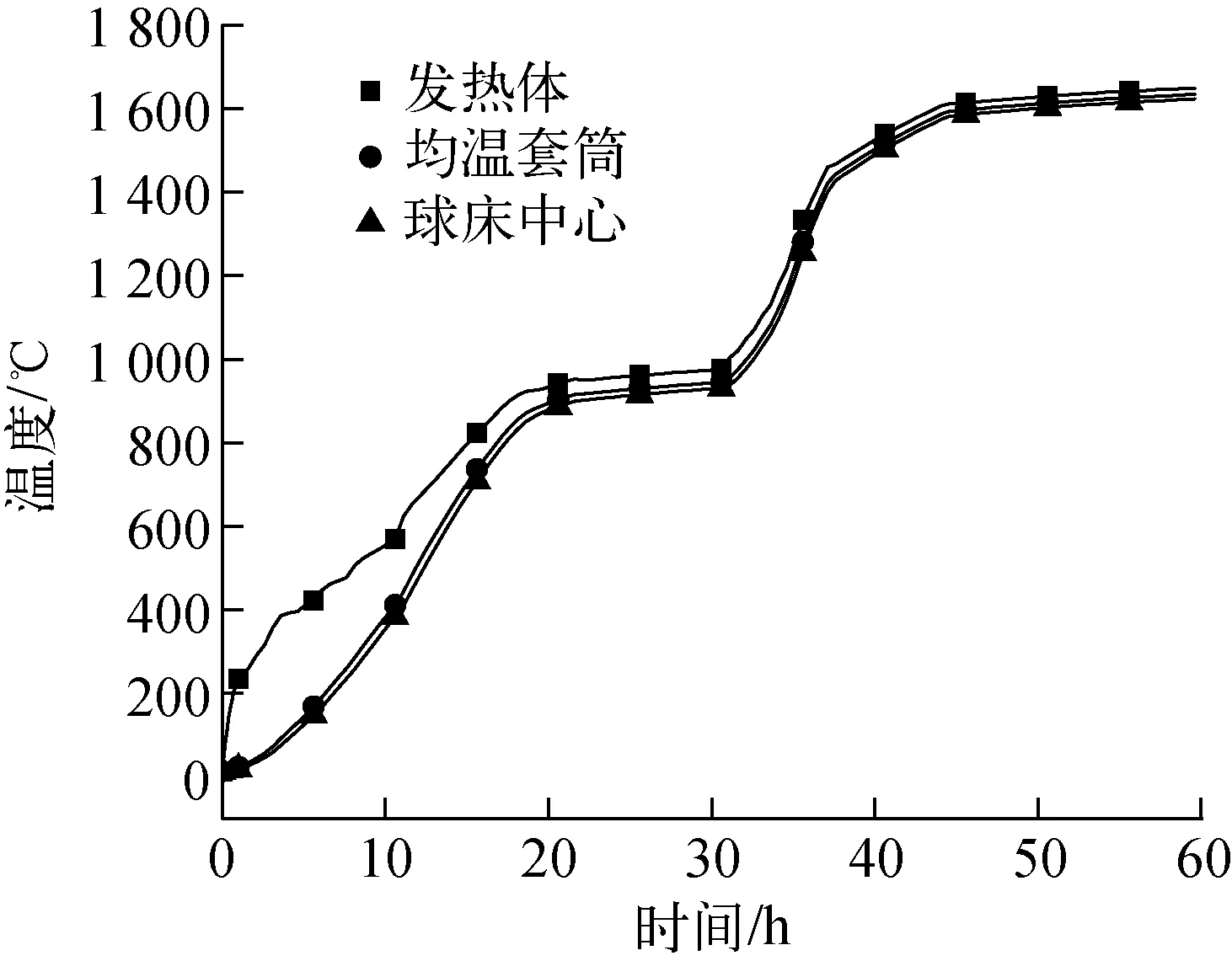
图11 实际加热功率时发热体和球床温度Fig.11 Temperature of heater and pebble bed with real heating power
实验中拟采取的另一种加热方式是采用1 600 ℃时的保温功率加热,在整个加热过程中,功率维持不变,但由于之前担心加热开始即采用大功率加热有可能使发热体超温损坏而未采用。图12为模拟计算得到的采用9.1 kW恒功率加热时发热体、均温套筒和球床中心的温度历史曲线。可见,发热体并未超温,但在加热开始的10 h内,发热体温度比球床温度高,最高时超过球床温度500 ℃,但温差会随着温度的升高而迅速减小,在1 600 ℃时,两者温差可忽略,可认为球床区温度即可代表发热体温度。
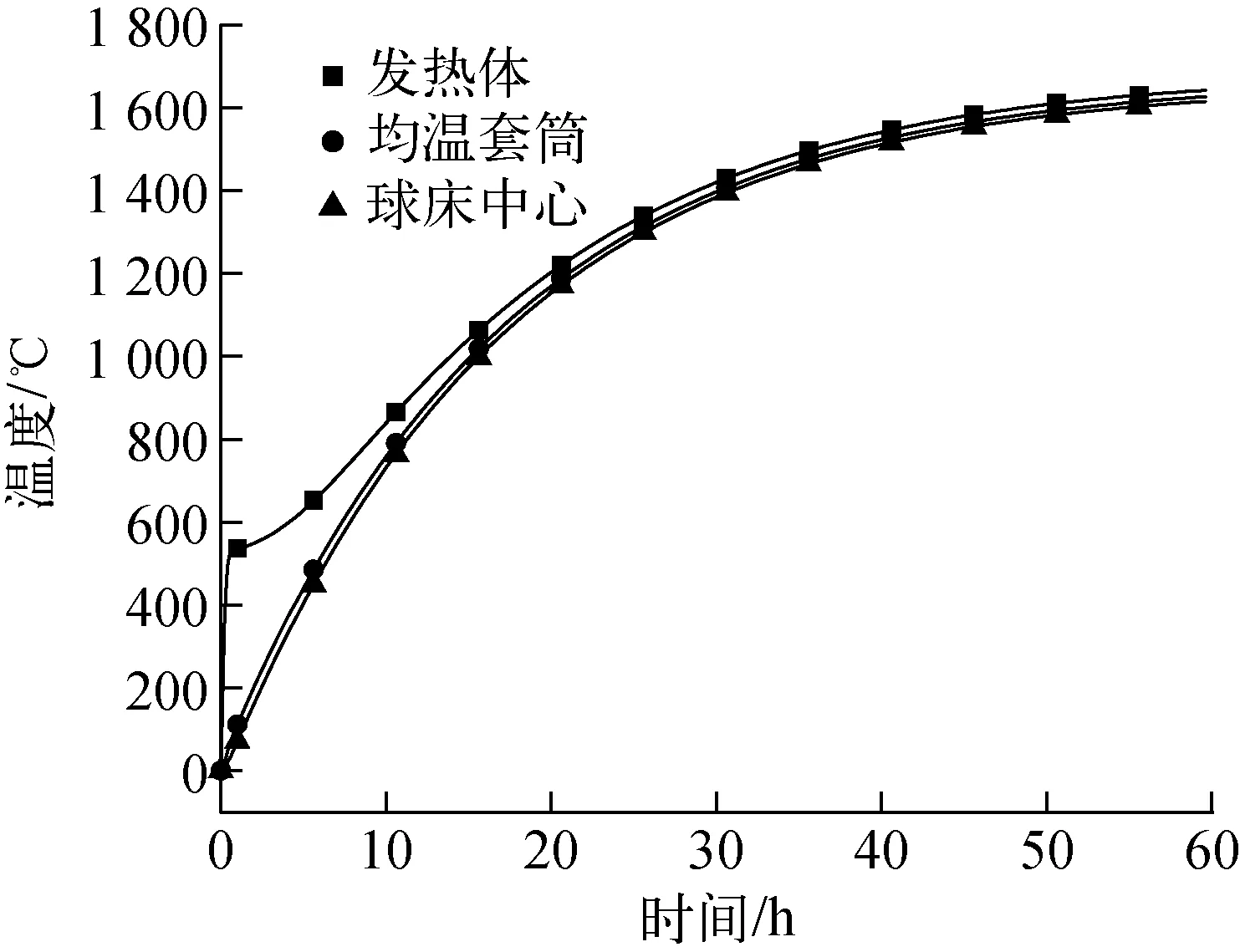
图12 恒功率9.1 kW加热时发热体和球床温度Fig.12 Temperature of heater and pebble bed with static heating power of 9.1 kW
功率逐渐增加方案和直接采用稳态功率加热方案相比,在升温的初始阶段,发热体与球床区温差更大,但温度升高后温差迅速缩小,两种加热方案都不会引起发热体超温。
发热体在加热开始阶段较球床温度高,并随温度升高温差消失,这一现象是由于发热体到球床的传热包含辐射环节,在低温时,辐射热阻很大,导致热量不能及时向外传导。温度升高,辐射传热能量增强,温差减小。
4 结论
模拟高温气冷堆温度、环境氛围的材料测试装置对于高温气冷堆相关材料研究具有基础性的作用。本文通过合理简化手段,建立了该实验装置在真空、辐射条件下的二维数学物理仿真模型,可用于研究表面辐射和固体导热共同作用下的传热机理,解释实验过程中发热体在加热过程中短时间超温等多种动态传热现象,预测发热体最高温度、轴向温度分布等难以直接测量的物理量,对实验过程中加热功率选择等方面具有很好的指导作用。
[1] WU Z, LIN D, ZHONG D. The design features of the HTR-10[J]. Nuclear Engineering and Design, 2002, 218(1-3): 25-32.
[2] NIESSEN H, BALL S. Heat transport and afterheat removal for gas cooled reactors under accident conditions, IAEA-TECDOC-1163[R]. Vienna: IAEA, 2001.
[3] 李聪新. 球床等效导热系数实验关键材料试验装置[D]. 北京:清华大学,2011.
[4] LI Congxin, REN Cheng, YANG Xingtuan, et al. Temperature measuring system in high temperature carbon reducing environment[C]∥ICONE21. Chengdu: [s. n.], 2013.
[5] REN Cheng, YANG Xingtuan, LI Congxin, et al. Design of the essential material test equipment for the pebble bed effective thermal conductivity measurement experiment[C]∥ICONE21. Chengdu: [s. n.], 2013.
[6] van ANTWERPEN W, ROUSSEAU P G, du TOIT C G. Multi-sphere unit cell model to calculate the effective thermal conductivity in packed pebble beds of mono-sized spheres[J]. Nuclear Engineering and Design, 2012, 247: 183-201.
[7] van ANTWERPEN W, du TOIT C G, ROUSSEAU P G. A review of correlations to model the packing structure and effective thermal conductivity in packed beds of mono-sized spherical particles[J]. Nuclear Engineering and Design, 2010, 240(7): 1 803-1 818.
[8] van ANTWERPEN W. Modelling the effective thermal conductivity in the near-wall region of a packed pebble bed[D]. South Africa: North-West University, 2009.
[9] LOGTENBERG S A, DIXON A G. Computational fluid dynamics studies of fixed bed heat transfer[J]. Chemical Engineering and Processing: Process Intensification, 1998, 37(1): 7-21.
[10]DIXON A G, NIJEMEISLAND M. CFD as a design tool for fixed-bed reactors[J]. Industrial & Engineering Chemistry Research, 2001, 40(23): 5 246-5 254.
[11]BEHNAM M, DIXON A G, NIJEMEISLAND M, et al. A new approach to fixed bed radial heat transfer modeling using velocity fields from computational fluid dynamics simulations[J]. Industrial & Engineering Chemistry Research, 2013, 52(44): 15 244-15 261.
[12]SHAMS A, ROELOFS F, KOMEN E, et al. Quasi-direct numerical simulation of a pebble bed configuration, Part Ⅱ: Temperature field analysis[J]. Nuclear Engineering and Design, 2013, 263(1): 490-499.
[13]PITSO M L. Characterization of long range radiation heat transfer in packed pebble beds[D]. South Africa: North-West University, 2011.
Modeling and Analysis of Dynamic Heat Transfer Characterization of Environment Simulating Facility for High Temperature Gas-cooled Reactor
LI Cong-xin, REN Cheng, YANG Xing-tuan*, JIANG Sheng-yao, SUN Yan-fei
(KeyLaboratoryofAdvancedReactorEngineeringandSafetyofMinistryofEducation,InstituteofNuclearandNewEnergyTechnology,TsinghuaUniversity,Beijing100084,China)
A material performance test facility simulating the temperature and environment was built by Institute of Nuclear and New Energy Technology (INET) of Tsinghua University, by which kinds of tests at high temperatures of 1 600 ℃ and below in carbon reducing environment could be conducted. Through rational simplification of the facility, the 2D mathematical model of the facility was introduced, which could simulate the dynamic heat transfer characterization including radiation and conduction at high temperature and under vacuum conduction. The simulating result is coincident with the measured temperature tendency and lots of dynamic heat transfer phenomenon observed in experiments could be explained. Furthermore, some key parameters which are difficult to be measured directly can be evaluated by the model, such as the radial temperature distribution of material test zone, the maximum temperature of the heater with different heating powers, which could give some instructive suggestions to further experiments.
high temperature gas-cooled reactor; environment simulating facility; high temperature; vacuum; radiation heat transfer
2014-02-04;
2014-03-23
高等学校博士学科点专项科研基金资助项目(20130002120015);清华大学自主科研计划资助项目(2014z21023);国家自然科学基金资助项目(11072131)
李聪新(1984—),男,河北衡水人,博士研究生,核能科学与工程专业
*通信作者:杨星团,E-mail: yangxingtuan107@163.com
TL332
A
1000-6931(2015)06-1080-08
10.7538/yzk.2014.youxian.0009
