凸度测量中的散射校正研究

胡克敏，吴志芳，苗积臣，张玉爱，邢桂来

(清华大学 核能与新能源技术研究院 核检测技术北京市重点实验室，北京 100084)



凸度测量中的散射校正研究

胡克敏，吴志芳，苗积臣，张玉爱，邢桂来

(清华大学 核能与新能源技术研究院 核检测技术北京市重点实验室，北京 100084)

本文分别从被测钢板的宽度、厚度和射线能量等3个方面对散射的影响进行了研究。首先建立凸度测量系统的蒙特卡罗模拟计算简化模型，分析了单能情况下钢板宽度和厚度对散射因子(SPR)的影响；然后建立X光机能谱计算仿真模型，模拟出给定管电压下X光机输出射线的连续能谱，并提出用多个单能分段等效的方法来代替连续能谱，模拟在实际连续能谱情况下钢板散射分布的规律，其模拟结果与实验测量结果能较好地吻合。

蒙特卡罗；凸度测量；散射因子；能谱

清华大学核能与新能源技术研究院自主研发成功1∶1规模的X射线热轧钢板凸度在线检测系统工业样机，对0.9～25 mm厚度的被测钢板，达±0.1%的测量精度。凸度测量实质上是对钢板横断面厚度分布的测量，在恶劣的热轧现场，实现高精度、高稳定、高速度的测量，必须消除康普顿散射对测量精度的影响(即散射校正)。目前采用的散射校正方法是针对某一厚度的标准钢板，通过专门校正机构分别测出有无散射影响时的探测器输出，然后加以校正，此方法为枚举法，要提高测量精度，要求对足够多的不同钢号、不同厚度、不同宽度的标准钢板分别进行测量，形成一个散射校正数据库，因此，此方法工作量大、有局限性。本文采用蒙特卡罗模拟计算方法，研究钢板的厚度、宽度和射线能量等对散射的影响规律，简化和优化厚度/凸度测量中的散射校正。

1 凸度测量系统的蒙特卡罗简化模型

凸度测量系统的结构如图1所示，主要包括C形架(分为上臂、侧臂、下臂)、两个X光机射线源(S1、S2，位于C形架的上臂内)及射线探测系统(位于C形架的下臂内)，其中射线探测系统由两排电离室探测阵列组成，分别对应射线源S1、S2，每排探测器含有224个长条形电离室单元，每个电离室以自身一角点为基准沿水平直线排列，并保证其入射窗正对相应的射线源。

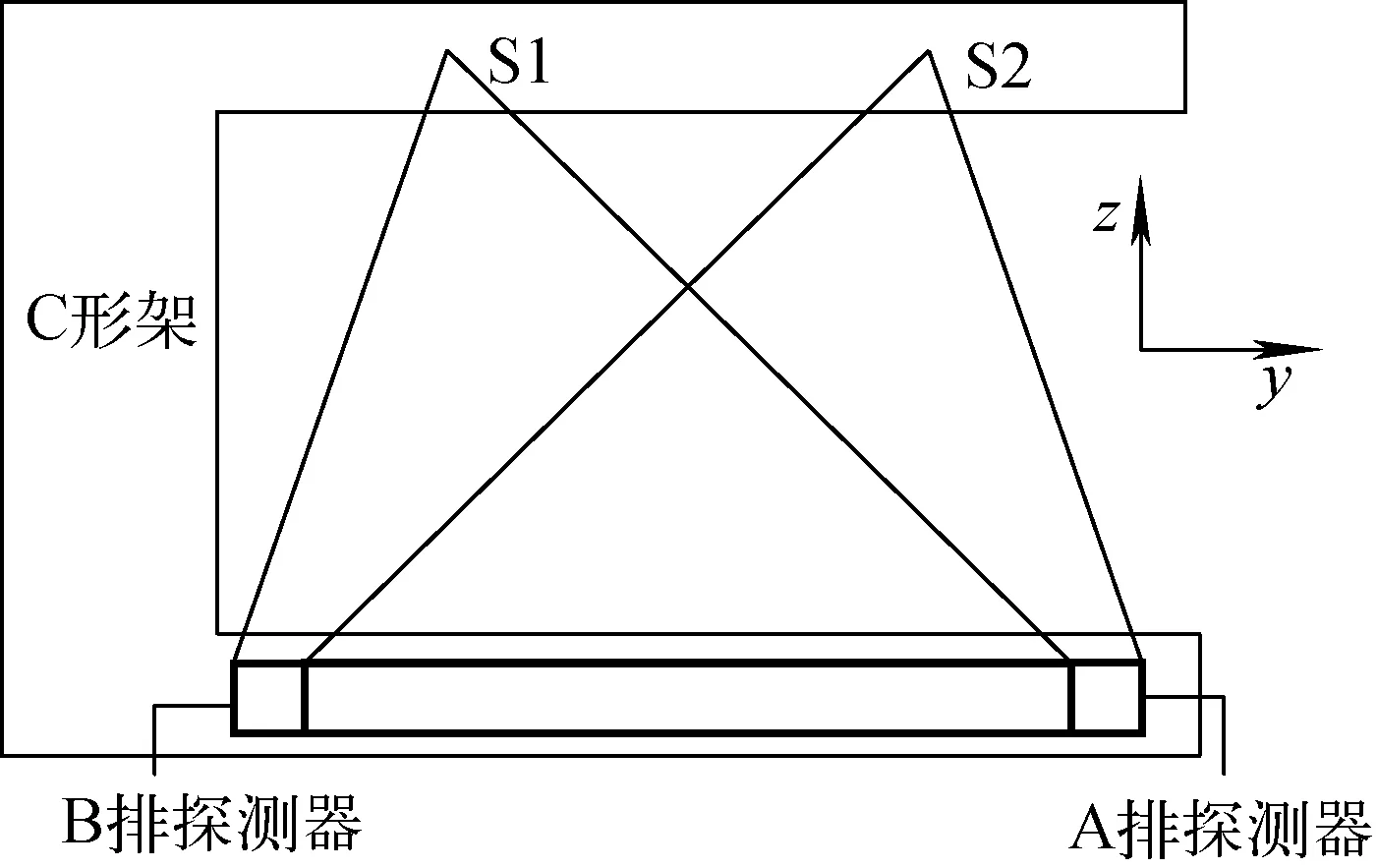
图1 凸度测量系统结构示意图Fig.1 Structure diagram of crown measurement

蒙特卡罗计算方法目前较常用的通用软件有MCNP、EGS、Geant4、FLUKA[1]，本文采用MCNP5软件。在MCNP5软件模拟计算中，将凸度测量结构简化为只有射线源-钢板-下臂模型，其中射线源的设置采用MCNP5软件中的CCC面源截取卡，用长方体栅元截取球面源的一部分来形成扇形射线束。探测单元的对源向心排列，采用trcl坐标变换卡实现。对下臂结构进行简化，图2为下臂结构简化后的横截面(x-z截面)示意图，仅保留射线束照射区域的结构部件，其尺寸和位置等参数设置均与凸度测量系统实验样机保持一致，下臂外围由等效的304不锈钢板代替。凸度测量系统在MCNP5可视化界面中的简化模型如图3所示。

图2 下臂简化模型示意图Fig.2 Scheme of simplified lower arm model

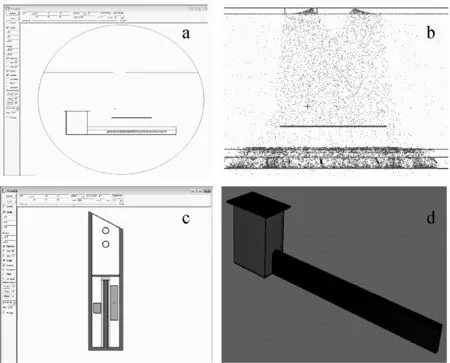
a——凸度测量系统模型y-z剖面图；b——扇形射线束粒子径迹；c——下臂模型x-z剖面图；d——下臂模型3D外形

2 单能情况下钢板宽度、厚度对散射分布的影响

入射光子与被测钢板发生相互作用后会形成透射光子和散射光子，二者均会对探测器输出做出贡献，但仅有透射光子的探测器响应贡献对应被测钢板的厚度，而散射光子则会造成相邻其他探测器的响应贡献，这进一步引起相应探测器位置的钢板厚度的测量误差。散射光子的探测器响应贡献显然与钢板宽度、厚度等因素有关，为定量分析，引入散射因子(SPR)的概念，对应每一路探测单元，其定义为：

(1)

2.1 钢板宽度对散射分布的影响

设定射线能量为180 keV，被测钢板为304不锈钢，钢板厚度为5 mm，钢板宽度分别为100、140、170 cm和无限宽。MCNP5计算结果如图4所示。

由图4可知，对厚度相同而宽度不同的钢板，A、B两排探测器在钢板中间位置，无论是输出总量、一次散射量、两次散射量还是SPR均几乎完全一致，仅边缘处略有不同，离射线源距离越远、钢板厚度越大、粒子散射次数越多，其边缘效应影响的探测单元范围越大。这说明，在钢板中间处散射光子的贡献不随钢板宽度的变化而改变，而在钢板边缘处散射光子的贡献比重随钢板宽度的变化有所变化。图4中曲线中间处左右不对称且不是水平直线，是因为各探测单元至射线源的距离不同，且射线源不位于钢板中间正上方。对于5 mm厚的304不锈钢板，中间处的散射贡献约占10%，而测量精度要求达到±0.1%，这说明测量凸度/厚度时必需进行散射校正。

由此可设想，对钢板厚度进行散射校正时，可分为两部分进行处理，中间部分的SPR仅与钢板厚度有关，可按无限宽钢板的情况处理而不考虑宽度，而边缘处则需单独处理。

2.2 钢板厚度对散射分布的影响

假定射线能量为180 keV，对304不锈钢制作的一系列不同厚度(1、5、10 mm)的钢板进行模拟计算，钢板宽度均为170 cm。模拟计算结果如图5所示。

由图5可知，钢板宽度相同的情况下，散射的贡献随钢板厚度的增加而增大，钢板厚为1 mm时散射的贡献约为8.9%，厚为5 mm时散射的贡献约为10%，厚为10 mm时散射的贡献约为11.2%。因此，只要测量出散射贡献随钢板厚度的变化曲线，就可对测量厚度进行散射校正。

图4 不同钢板宽度时输出总量、一次/二次散射量及SPR分布曲线Fig.4 Total output, once/twice scattering amount and SPR curves of different width steel plates

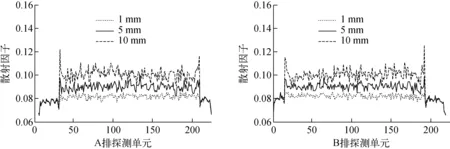
图5 钢板厚度不同时SPR分布曲线Fig.5 SPR curves of steel plates with different thicknesses

图6为B排17个不同位置探测器的SPR随钢板厚度的变化曲线，其中，钢板宽度为170 cm。可看出，对170 cm宽度钢板(其边界对应第16路和第192路探测器)，16、17、18、192、193等5路探测器因处于或靠近钢板边缘，其散射影响随钢板厚度的变化差距较大，需单独校正；其他各路探测器的SPR随厚度的增大呈线性增大的趋势，且斜率随探测器的位置变化不大，这对实际散射校正具有重要的指导意义。

图6 B排不同位置探测器的SPR随钢板厚度的变化曲线Fig.6 SPR curve vs thickness of steel plate for different position detectors

3 连续能谱情况下SPR的变化

射线源选用的是X光机，其输出射线具有连续能谱，因此，需进一步研究或验证采用多能或连续能谱射线时散射对钢板厚度测量的影响。

3.1 X光机能谱的模拟计算

凸度测量系统样机中使用的X光管型号为Comet MXR-225/02/FB，其中，靶材料为钨，固有滤片为(1.0±0.1) mm的铍，发射角为30°。管电压为180 kV时，X射线的能谱模拟计算结果如图7所示。

图7 模拟计算的X光机能谱Fig.7 Simulation result of X-ray machine energy spectrum

3.2 分段等效单能代替连续能谱的计算分析[2]

射线与钢板的相互作用与射线能量相关。在凸度测量系统中，入射射线为连续能谱，若对每个能量的射线均进行分析计算，则过于复杂繁琐，几乎无法实现。因此，本文采用分段等效单能的方法简化连续能谱，即把整个连续能谱分成若干能段，每个能段用一个单能值表示。图8为将整个能谱分成5段后的结果，其中，E(i)为每个能段的能量值，W(i)为能段对应的归一化粒子权重因子。

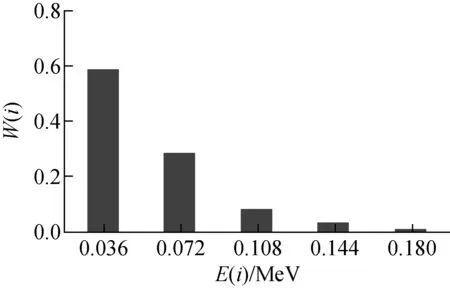
图8 简化能谱柱状图Fig.8 Simplified histogram of energy spectrum

假设将整个能谱分成N段，则N越大，计算结果越接近实际的连续能谱，当N趋近∞时，计算结果等同于实际的连续能谱。

分别计算每个能段的单能扇形射线束穿透被测钢板后对探测器输出的贡献，设某一单能射线束下探测单元的总输出为DS(i)，不含散射光子贡献时的输出为DN(i)，其中i=1,2，…N，再将对应各能段的探测单元输出值分别按式(2)、(3)加权求和，得到等效连续能谱下，包含散射的探测单元的总输出DST、不含散射时的探测单元输出DNT，则SPR的计算方法如式(4)所示。

(2)

(3)

(4)

3.3 仿真结果的分析比较

对厚为15 mm、宽为170 cm的钢板，分别仿真计算了其在180 keV单能射线、分段等效单能射线(取N=5)及全能谱射线作用下的SPR分布曲线，并将仿真计算结果与实验测量值对比，结果如图9所示。

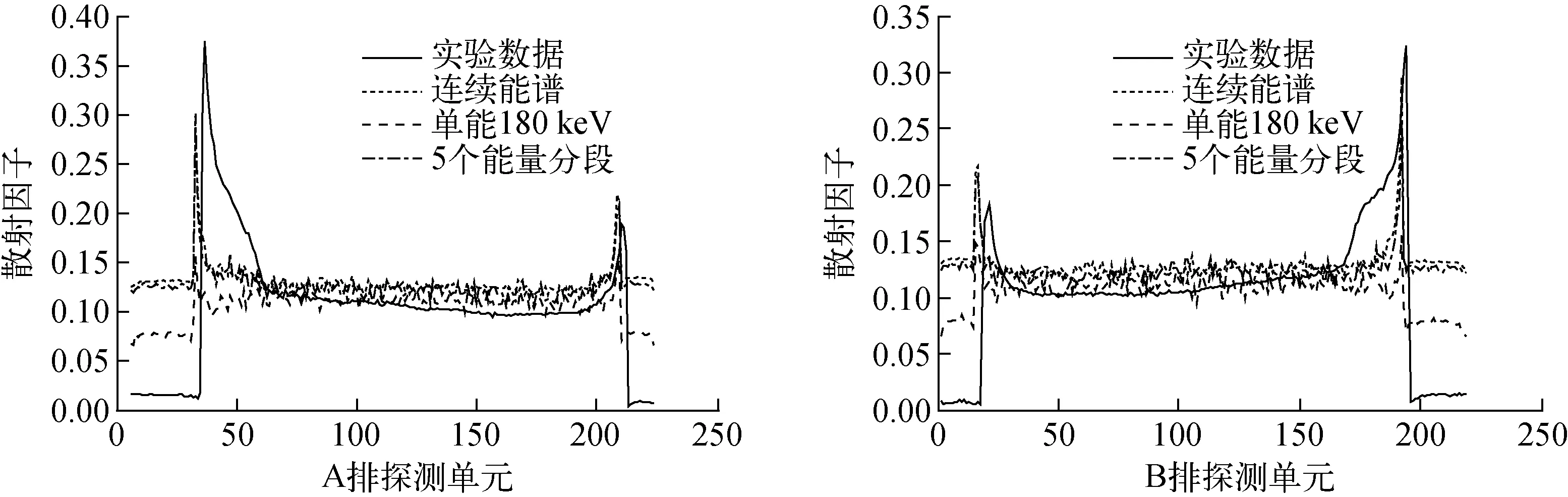
图9 3种情况下的模拟计算值与实验测量值的对比分析Fig.9 Contrastive analysis of simulation value and experimental measurement value

由图9可看出，分段等效单能方法的计算结果与连续能谱结果相当，较单能情况下更趋近于实验测量值，与实验测量值符合较好。这说明采用分段等效单能方法处理连续能谱是可行的。

因此，在实际应用中，采用分段等效单能的方法，可通过少量实测数据的刻度与校正，实现实际全能谱下测量结果的较好近似。

4 结论

本文通过蒙特卡罗模拟方法，分别研究了单能和连续能谱情况下SPR与钢板宽度、厚度的关系，并提出了连续能谱简化分析的方法，模拟结果与实际实验测量结果相吻合，对实际凸度测量中的散射校正提供了技术指导，具有很好的实用价值。

[1] 邱睿，李君利，武祯，等. 四种蒙特卡罗程序的比较计算[J]. 原子能科学技术，2008，42(12)：1 149-1 152.

QIU Rui, LI Junli, WU Zhen, et al. Comparison calculation of four Monte-Carlo codes[J]. Atomic Energy Science and Technology, 2008, 42(12): 1 149-1 152(in Chinese).

[2] 陈慧娟，潘晋孝. 一种基于多能统计的射束硬化校正方法[J]. CT理论与应用研究，2010，19(1)：21-27.

CHEN Huijuan, PAN Jinxiao. A beam-hardening correction method based on poly-energetic statistics in X-ray CT[J]. CT Theory and Applications, 2010, 19(1): 21-27(in Chinese).

Study on Scattering Correction in Crown Measurement

HU Ke-min, WU Zhi-fang, MIAO Ji-chen, ZHANG Yu-ai, XING Gui-lai

(BeijingKeyLaboratoryonNuclearDetection&MeasurementTechnology,InstituteofNuclearandNewEnergyTechnology,TsinghuaUniversity,Beijing100084,China)

The influence of the scattering was researched from three aspects about the width and thickness of steel plate and ray energy. The simplified Monte-Carlo model of the crown measurement was built, and the influence of the width and thickness of the plate on the distribution of scattering factor was analyzed. The X-ray spectrum simulation model was established, based on which the X-ray continuous energy spectrum under a given tube voltage was simulated. And then an equivalent method was put forward to use multiple single energy to replace the actual continuous spectrum during the calculation of the scattering distribution rule in practice. In the contrast, the simulation results can well accord with the experimental measurement results.

Monte-Carlo; crown measurement; scattering factor; energy spectrum

2014-03-18;

2014-09-14

北京市科委研发攻关课题资助项目(Z080903027508)

胡克敏(1985—)，女，山东滕州人，博士研究生，核科学与技术专业

TL99

A

1000-6931(2015)07-1325-05

10.7538/yzk.2015.49.07.1325