基于平衡防渗原理的土石坝防渗帷幕优化设计

党发宁，田红梅，王振华，2

(1.西安理工大学岩土工程研究所，陕西 西安 710048;2.中国电力工程顾问集团西北电力设计院有限公司，陕西 西安 710075)

为了确定防渗帷幕的合理深度、长度以及厚度，国内外学者从理论、实验以及数值分析等方面做了大量研究:尹海华［1］认为当仅从渗流量角度考虑时，竖直防渗帷幕深度是坝前水深的10～16倍时防渗效果比较理想;谢兴华等［2］认为防渗帷幕的最优深度与覆盖层深度有关，当防渗帷幕的深度与覆盖层的深度比值为0.6～0.8时，防渗效果最好;黄洪海［3］认为防渗帷幕的深度应按岩层的透水性以单位吸水量作为帷幕深度的依据，当坝高大于70m，帷幕深度应达到1 Lu值漏水量的范围以下;当坝高在30～69 m时，帷幕深度在3 Lu值范围以下;当坝高小于30m时，帷幕深度应达到5 Lu值范围以下;王汉辉等［4］认为，帷幕深度应按坝高(水头)的倍数确定，常用经验公式为帷幕深度等于坝前最大水深加上一个常数，这个常数一般取8～25m;宋玉田等［5］认为坝高与幕深的关系为幕深等于坝高与幕深系数之积，幕深系数一般取0.6～1.9，坝高与幕长的经验公式为幕长等于坝高与幕长系数之积，幕长系数一般取3.4～15.7;黄朝煊等［6］认为当防渗帷幕深度超过1倍的坝底宽时，随着防渗帷幕深度的增加对扬压力的抑制作用不明显;郑伦鑫等［7］得出一般情况下的帷幕厚度与灌浆材料的最优组合，可为坝基防渗优化设计提供参考。由以上研究成果可见，各种水工设计规范对大坝渗流量控制既无统一认识，工程实践中也无统一标准;同时，防渗帷幕尺寸既与坝前水头有关，又与地层的渗透系数有关，任何只考虑单一因素确定帷幕尺寸的方法都是不全面或不合理的。

垂直防渗的布置原则是“前堵后排”，大部分工程通过前堵来实现防渗目的，即通过填充、挤密、置换、冻结及其他物理化学作用等方法在土层中形成一个垂直的防渗墙体，使其达到阻水的目的。设计合理的防渗帷幕可以有效改善坝基的渗流状态，满足渗透稳定要求，并可显著降低渗流的浸润面、出逸段的高度以及渗流量。对于无隔水层或相对隔水层埋深较大，帷幕深度难以达到隔水层的水利工程而言，常采用悬挂式防渗帷幕。设计不合理的悬挂式防渗帷幕可能存在未达到截渗的目的、帷幕后的渗透流量和渗透坡降仍然很大等问题［8］。因此，研究如何恰当选取悬挂式防渗帷幕深度、长度和厚度，成为防渗帷幕研究的一个新的课题［9］。

本文依据渗流控制原理［10］，在满足渗透稳定(i＜［icr］)和渗流量控制标准的前提下，提出了防渗帷幕采用“深度→长度→厚度”依次确定，且控制各部位的渗流速度大致相等的“平衡防渗法”，并通过工程算例验证了这一方法的可靠性。该方法既可保证帷幕防渗效果达到最佳，又可保证投资达到最小。

1 基于平衡防渗原理的优化设计

针对各种现行水工规范对防渗帷幕尺寸的确定既无统一认识、工程实践中也无统一标准问题，本文提出防渗帷幕采用“深度→长度→厚度”依次确定的优化设计方法，即以渗漏量和坡降为控制标准优先确定防渗帷幕深度，再以两岸绕渗速度等于坝基渗流速度确定帷幕长度，最后以坝基覆盖层中最大渗流速度等于穿过帷幕的最大渗流速度确定防渗帷幕厚度的设计方法。按以上方法确定防渗帷幕的结构尺寸，可保证工程区各部位的渗流得到平衡控制，既不会形成主渗流通道，也不会在某个部位防渗过当，本文称之为“平衡防渗法”。

1.1 坝基中防渗帷幕深度的确定

若隔水层(相对不透水层)在坝基河床下埋深较浅，应选择封闭式帷幕。帷幕应深入隔水层顶板下5～10m，局部地质缺陷部位应适当加深。

若无隔水层或隔水层(相对不透水层)埋深较大，帷幕深度难以达到隔水层的，可根据工程需要，选择采用悬挂式帷幕。确定悬挂式帷幕深度的方法有3种:①按规范规定的防渗线控制法;②渗流量控制法;③水力坡降控制法。

国内主要水工建筑物规范规定的防渗线控制标准见表1。

表1 国内主要水工建筑物规范规定的防渗设计标准

国内主要水工建筑物规范规定的渗流量控制标准为:抽水蓄能电站上库的渗流量应小于库容的0.05%，其他水工建筑物的渗流量按多年枯水期来水量的1%来控制。

水工建筑物的水力坡降控制标准为:渗流计算的各种材料的水力坡降小于其允许水力坡降。

实际设计时，可按规范规定的防渗线控制法确定出坝基及两岸帷幕的初始设防范围，然后计算渗透流量和水力坡降，用渗透流量控制法和水力坡降控制法确定出河床帷幕的最终设计深度。

在满足以上3个控制标准的前提下，帷幕深度也不是越深越好，而是存在一个临界值。帷幕的深度超过该值时渗透水流将选择直接穿过帷幕上部而不是从帷幕底部绕渗，就是说超过以上深度的防渗帷幕实际上是无效的。在地层材料和帷幕厚度确定的条件下帷幕的临界深度可以用绕过帷幕的渗流速度等于穿过帷幕的渗流速度来确定。

1.2 左右岸防渗帷幕长度的确定

在确定了坝基中防渗帷幕的最终设计深度以后，第二步在初拟的左右岸防渗帷幕长度的基础上确定防渗帷幕的最终设计长度，方法如下:在满足坝体渗透稳定(i＜［icr］)和渗流量控制标准的前提下，控制两岸的最大绕渗速度v岸等于防渗帷幕上下游地层中的最大绕渗速度v河，即v岸=v河，将达西定律代入得

式中:H是大坝上下游水头差;2L岸为左右岸的绕渗路径长度，为防渗帷幕长度L岸的2倍;2D河为河床覆盖层中绕过帷幕底部的渗透路径长度，为防渗帷幕的深度D河的2倍;K岸和K河分别为两岸岩体和坝基覆盖层(基岩)的渗透系数。若河床为多层覆盖层土，则河床覆盖层的等效渗透系数［11］为

式中:D为地层厚度;Di为第i个地层的厚度;Ki为第i个地层的渗透系数，m为地层总数。若左右岸为多层水平岩层，则左右岸的渗透系数可按各材料分区独立选取，独立设计。若分层较多，层厚较小，各层渗透系数差别不大，独立设计困难，可按下式计算等效渗透系数［11］:

经换算可得防渗帷幕的长度公式为

1.3 防渗帷幕厚度的确定

第三步确定防渗帷幕的厚度。与上述确定防渗帷幕长度的原理类似，建议防渗帷幕厚度按以下公式确定:在满足坝体渗透稳定(i＜［icr］)和渗流量控制标准的前提下，穿过防渗帷幕的最大渗流速度v幕等于防渗帷幕上下游地层中的最大绕渗速度v河，即v幕=v河，代入达西定律得

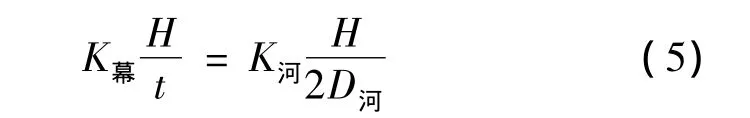
式中:t为防渗帷幕的厚度;K幕为防渗帷幕的渗透系数。

经换算可得防渗帷幕的厚度公式为

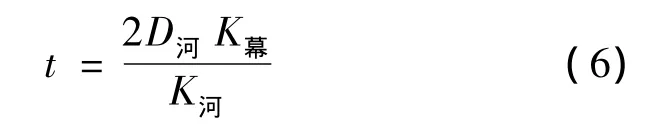
当防渗帷幕的长度和厚度超过以上计算值时，渗透水流优先选择从河床帷幕下方绕渗到达下游;当帷幕的厚度小于此值时，渗透水流优先选择穿越帷幕到达下游;当帷幕的长度小于此值时，渗透水流优先选择从左右两岸绕渗到达下游。说明按以上方法确定的左右岸防渗帷幕长度和厚度，既满足了防渗控制要求，又达到了最大程度节约投资的目的，是一种最优设计方法。

工程实践中，钻孔灌浆区防渗帷幕厚度的确定，应取图1中d所示的厚度。图中I区为灌浆效果好的区域，Ⅱ区为灌浆效果差的区域，对于Ⅲ区而言，虽然处于灌浆效果差的区域，但是经过两次灌浆，理论上认为Ⅲ区与I区的灌浆效果相当，所以防渗帷幕的厚度d确定为图1所示区域较为合理，渗透系数按I区灌浆效果时选取。至于扩散半径R不仅与渗透系数有关，还与孔隙度有关，而且孔隙度较渗透系数对扩散半径有着更大的影响［12］。

图1 帷幕灌浆效果示意图

2 算例分析

2.1 工程概况

某水电站位于四川省阿坝州境内的大渡河干流上，是金川—丹巴河段分三级开发的第一级电站，电站装机380mW。该工程最大坝高66.0m，为二等大(2)型工程，拦河坝为2级建筑物，设防地震烈度7度。可行性研究阶段比选推荐坝型为沥青混凝土心墙堆石坝。

坝址区河流流向约 NE81°，枯水期河水位2082.00m，相应河水面宽60～85m，河道纵坡降约0.1%。正常蓄水位2130m，相应谷宽311～317 m。河谷呈岸坡对称的“V”形，属高山峡谷地貌。坝址区基岩为三叠系上统侏倭组()变质砂岩、燕山晚期()似斑状黑云花岗岩;第四系主要有冲积物()、洪积物、崩坡积物及阶地堆积物()等。根据其物质组成、结构特征、工程特性等，坝轴线剖面从上向下可分为7大层和7个夹层或透镜体:①粉砂层;②含砂含漂卵石砾石，包括②-1中粗砂、②-2中粗砂、②-3含砾砂3个子层;③含卵含砾中粗砂;④含砂含漂卵石，包括④-1细砂、④-2含卵中粗砂、④-3含卵中粗砂、④-4含卵含砾中砂4个子层;⑤含卵含砾中砂;⑥含砂含砾漂石卵石;⑦含卵含砾中砂。

该水电站渗流计算区域内共涉及28种材料，本文计算用到的参数如表2所示。

表2 大坝渗流与稳定计算参数

2.2 防渗帷幕优化设计

a.深度的确定。该工程为二等大(2)型工程，根据规范规定，防渗帷幕应深入q≤3 Lu的地层。为确保坝基的渗透稳定，坝基下帷幕应深入3 Lu线以下5.0m，形成全封闭式防渗帷幕，深度为87 m。防渗帷幕伸入两岸的长度按水库正常蓄水位与两岸水库蓄水前的地下水位相交处确定，初步定为左岸95m，右岸120m。

b.长度计算。将表2中的参数代入式(2)(3)可得K河=5.23×10－7m，K左岸=5.84×10－7m/s，K右岸=6.82 ×10－7m/s，再由式(4)可计算得 L左岸=97.1 m，L右岸=113.5m。

c.厚度计算。将表2中的参数代入式(6)可计算得t=0.998 m。

2.3 三维渗流有限元计算

利用seep-3d有限元分析软件，建立三维有限元模型。模型采用笛卡尔直角坐标系，横河向坐标x原点选取在河床中心处，顺河向坐标y原点选取在心墙中心处，垂直向坐标z原点选取在零标高处。采用前面计算得到的防渗帷幕的深度、长度以及厚度进行有限元计算，并对设计方案进行敏感性分析。有限元计算采用六面体网格，整个模型共划分出100133个节点，107926个单元，模型及网格划分结果如图2所示。分4种工况计算。

图2 大坝渗流计算模型单元网格划分

a.工况1:按设计防渗方案(厚1 m、深87 m的混凝土防渗帷幕，左、右两岸防渗帷幕延伸长度分别为97 m和113 m)进行渗流计算。坝上游正常蓄水位2130.00m，下游相应水位2081.45m。

b.工况2:防渗帷幕厚1.2m，其他计算参数同工况1。

c.工况3:两岸扩大防渗帷幕延伸长度方案(左岸260m及右岸311 m)，其他计算参数同工况1。

d.工况4:防渗帷幕底部向上15m范围开叉，其他计算参数同工况1。

大坝各关键部位的渗流量及总渗流量、最大水力坡降、渗流速度的计算结果分别见表3、表4和表5。

表3 各工况关键部位渗流量及总渗流量 L/s

表4 各工况关键部位的最大水力坡降

表5 各工况关键部位的流速 m/s

由表3各工况关键部位的渗流量汇总结果可知:工况1总渗流量为13.164 L/s，总体渗流量很小，沥青混凝土心墙、防渗帷幕以及大坝下游渗流出口处等部位的最大水力坡降均小于其允许水力坡降，但靠近左岸的堆石体在渗流出口处的最大水力坡降已达到1.554，超过堆石体的允许水力坡降，应对左岸靠近山体的堆石体进行局部保护。从图3和图4坝底高程2062m处水平剖面以及大坝心墙处顺河剖面处的水头等值线图可以看出:工况1中87 m的防渗帷幕深度可以有效降低大坝上下游水头。

图3 大坝底高程2062m处水平剖面上的水头等值线(单位:m)

图4 大坝在x=115m处顺河剖面上的水头等值线(单位:m)

工况2在工况1的基础上增加防渗帷幕厚度到1.2m后，总渗流量为12.89 L/s，与工况1的计算结果相比，渗流量略有下降，但下降幅度不大;靠近左岸的堆石体在渗流出口处的最大水力坡降为1.647，略大于工况1的1.554，应对左岸靠近山体的堆石体进行保护。总体而言:工况2与工况1计算结果相比无明显差异，说明加厚防渗帷幕不能有效减少大坝的总体渗流量。

工况3在工况1的基础上增加两岸防渗帷幕的延伸范围后，总渗流量为13.455 L/s，与工况1的计算结果相比渗流量略有减小。靠近左岸的堆石体在渗流出口处的最大水力坡降为1.645，略大于工况1的1.554，应对左岸靠近山体的堆石体进行保护。总体而言，工况3与工况1计算结果相比渗流量及各关键部位最大水力坡降略有减小，但减小幅度较小，说明增加两岸防渗帷幕的设防范围是不必要的。

工况4在工况1的基础上防渗帷幕底部向上15m开叉后，总渗流量为123.957 L/s，比工况1的总体渗流量大9.4倍，沥青混凝土心墙及防渗帷幕处最大水力坡降较工况1有一定程度的减小，渗流出口附近大坝堆石体中的水力坡降的最大值均比工况1有所提高，防渗帷幕水力坡降及堆石体靠近两岸位置的渗流出口处超过允许坡降，从而使整个下游堆石体不满足渗透稳定要求。由此说明防渗帷幕的深度对坝体总渗流量会产生很大影响，保证防渗帷幕的深度能够有效提高坝体的防渗效果。

综上所述，最终确定的防渗帷幕最优深度为87 m，向左、右两岸延伸防渗帷幕的最优长度分别取97 m及113 m，防渗帷幕厚度影响不是很显著，1 m为最优防渗帷幕厚度。可见基于本文提出的平衡防渗原理进行防渗方案的优化设计是可靠的。

3 结语

本文依据渗流控制原理，在满足渗透稳定(i＜［icr］)和渗流量控制标准的前提下，提出了大坝防渗体系设计的“平衡防渗法”，按此方法分别给出了防渗帷幕深度、长度、厚度的最优化设计计算方法，并以某水电站防渗系统设计为例进行设计计算，再通过三维有限元软件的计算结果进行分析，验证了防渗帷幕设计深度、长度以及厚度的合理性。本文理论部分以防渗帷幕为例论述，其原理对防渗墙的设计同样适用。

［1］尹海华.无限深土石坝坝基悬挂式垂直防渗体防渗方法初探［J］.甘肃水利水电技术，2012，48(7):32-35.(YIN Haihua.Study on seepage body in infinite deep foundation for embankment dams seepage prevention［J］.Gansu Water Resources and Hydropower Technology，2012，48(7):32-35.(in Chinese))

［2］谢兴华，王国庆.深厚覆盖层坝基防渗墙深度研究［J］.岩土力学，2009，30(9):2708-2712.(XIE Xinghua，WANG Guoqing.A study of anti-seepage wall depth in thick overburden dam base［J］.Rock and Soil Mechanics，2009，30(9):2708-2712.(in Chinese))

［3］黄洪海.岩溶水库坝基防渗帷幕灌浆幕深与幕长的结构形式及处理［J］.贵州地质，2003，20(4):223-227.(HUANG Honghai.Structural form and treatments on the curtain depth and length of curtain-grouting preventing to seepage of dam foundation of reservoirs in karst area［J］.Guizhou Geology，2003，20(4):223-227.(in Chinese))

［4］王汉辉，邹德兵，夏传星，等.水利水电工程中防渗帷幕布置原则与方法［J］.水利与建筑工程学报，2010，8(6):117-120.(WANG Hanhui，ZOU Debing，XIA Chuanxing，et al.Principles and methods of impervious curtain layout in water conservancy and hydro-power engineerings［J］.Journal of Water Resources and Architectural Engineering，2010，8(6):117-120.(in Chinese))

［5］宋玉田，魏茂雪，齐永红.深基坑防渗帷幕插入深度的分析［J］.山东水利，2003(8):41-42.(SONG Yutian，WEImAoxue，QI Yonghong.Analysis of seepage curtain insertion depth in deep foundation［J］.Shandong Water Resources，2003(8):41-42.(in Chinese))

［6］黄朝煊，王贺瑶.坝基渗流与坝肩绕渗实用计算方法探讨［J］.水电能源科学，2015，33(3):72-75.HUANG Chaoxuan，WANG Heyao.Discussion on computing method of dam foundation seepage and bypass seepage of dam abutment［J］.Water Resource and Power，2015，33(3):72-75.(in Chinese))

［7］郑伦鑫，燕乔，张胜利，等.深厚砂砾石坝基防渗帷幕方案优化［J］.三峡大学学报:自然科学版，2015，37(3):1-5.(ZHENG Lunxin，YAN Qiao，ZHANG Shengli，et al.Deep sandy gravel dam foundation impervious curtain scheme optimization［J］.Journal of China Three Gorges University:Natural Sciences，2015，37(3):1-5.(in Chinese))

［8］蒋力.土石挡水建筑物防渗体布置形式对渗流计算结果的影响研究［D］.西安:西安理工大学，2011.

［9］王晓燕.悬挂式混凝土防渗墙深度优化设计研究［D］.西安:西安理工大学，2008.

［10］毛昶熙.渗流计算分析与控制［M］.北京:水利水电出版社，2003:155-158.

［11］冯国栋.土力学［M］.北京:中国水利水电出版社，1986:33-38.

［12］韩磊，陈建生，陈亮.帷幕灌浆扩散半径及数值模拟研究［J］.岩土力学，2012，33(7):2235-2240.(HAN Lei，CHEN Jiansheng，CHEN Liang.Research on diffusion radius and mumerical simulation in curtain grouting［J］.Rock and Soil Mechanics，2012，33(7):2235 ～ 2240.(in Chinese))