教学机智从哪儿来？

王九红

摘要：学生在课堂中表现出的行为具有其合理性，需要教师以教学机智来应对。全面而深刻理解的学科教学知识（PCK）是教师教学机智生成的前提条件。教师的学科教学知识动态表现为学科教学能力（PCA），在情感系统和信念系统的监控和调节下，经顿悟而生成教学机智。

关键词：教学机智;学科教学知识（PCK）;学科教学能力（PCA）;顿悟

中图分类号：G40 文献标志码：A 文章编号：1673-9094（2015）01-0036-06

《人民教育》2007年第7期刊登了俞正强的文章《不让一个学生落后》。文中有这样一则教学案例：

有这样一道题目：

××牌52型拖拉机，一天耕地150公亩，问12天耕地多少公亩？

一位学生是这样解的：52×150×12=（略）。

由于新接的班，对孩子不熟悉，所以俞老师就问：

告诉我，你为什么这么列式？

老师，我错了。

好的，告诉我，你认为正确的该怎么列式？

除。

怎么除？

大的除以小的。

为什么是除呢？

老师，我又错了。

你说，对的该是怎样呢？

应该把它们加起来。

看来，这位学生是在瞎猜。于是俞老师开始启发：

我们换一个题目，比如你每天吃2个大饼，5天吃几个大饼？

老师，我早上不吃大饼的。

那你吃什么？

我经常吃粽子。

好，那你每天吃2个粽子，5天吃几个粽子？

老师，我一天根本吃不了2个粽子。

那你能吃几个粽子？

吃半个就可以了。

好，那你每天吃半个（小数乘法没学）粽子，5天吃几个粽子？

两个半。

怎么算出来的？

2天一个，5天两个半。

面对这样的场景，作者产生了“这位学生的问题在哪里”的困惑，进而认为“这位学生的问题就在于数学思考的方式尚未建立起来，她需要的不是老师不断地重复讲这类题目，而是建立起与题目对应的数学语言，并运用数学语言间的数理关系进行演绎建构，形成我们通常所说的思维能力。因此，学生在学习解决问题之前，需要有一个问题解决工具的掌握过程，这个过程称为准备性学习。如果学生的学习发生困难，教师应该把力量花到与该学习相关的准备性材料上去。”郑毓信先生对此说得更为明白：这名学生所缺乏的并不是生活经验，而是数学抽象的能力。尽管这是一名四年级的学生，她还没有在“日常数学”向“学校数学”过渡上取得切实的进展。[1]

以上研究者关注的是“学生的问题出在哪里”。探寻并解决其问题具有毋庸置疑的价值，如果换一个角度看，我们也应注意到这样一个事实：对于有些学生而言，当他遇到一个具体的问题情境时，他不向着数学方面想，也不顺着教师的思路走，这完全是一种正常的现象。当这种情况出现时，教师当场要做的就是立刻拿出一个好的应对办法——机智地将教学引向良好的状况。显然，案例中的状况很不尽如人意，我们有必要从教师——进一步地从教师学科教学知识（PCK）的视角——进行深入的探究：教师的教学智慧在哪儿丢失？教师的教学智慧从哪儿来？

一、案例分析：教学机智的缺失

应该承认，本案例中“搞笑”场景出现的原因之一在于老师不能见机行事。古汉语中“机”字的意义有五：①弓弩上发射箭的机关。②关键，要点。③时机，机会。④机灵。⑤通“几”。事情的苗头或预兆。[2]综合以上词义，教学机智之“机”可以理解为教学现场中出现的灵活变动的、关键性的事件，这一事件预示着某些事情的发生，可能是事情转向好或坏的方面的机会。因为不见“机”，老师就看不到事情变化的苗头，就会抓不住关键，进而丧失机会，最终不能正确行事。具体看，案例中教师的不见机行事体现在两个方面：

首先，叫答不见机。

案例中教师被一步步地带到“沟里”其起始于教师的不当叫答：教师叫一个学业水平不高的学生来回答一个情境远离学生经验且具有多余条件的问题。

教师所提问题有两大特点：一是情境远离学生经验。学生不能理解“XX牌52型拖拉机”指的是什么？可能对拖拉机耕地这样的事情也不了解。由于缺乏相关的背景知识，所以学生不能完全了解题意，列出“52×150×12”这样的式子也在情理之中。PISA将求解的问题设定为四种情境，即个人情境、学校情境、公众情境、学术情境。对学生而言，距离学生最近的情境是学生的个人生活，其次是学校生活、职业生活和休闲生活，然后是日常生活中遇到的地方社区和社会生活，最远的是学术情境。显然，本案例中的问题情境属于公众情境，具体而言是一种农业生产的情境，对于这种情境，不要说现在城市里的孩子，就是城市里的成年人也未必非常熟识，比如，各种拖拉机的品牌、型号，它们各自的功率大小，每小时能耕多少公亩地等。学生将“52”也视作一个数量条件用到了算式中，这固然与没有掌握“每小时耕地公亩数×耕地时间=耕地总面积”这一数量关系有关，但肯定也与不理解“XX牌52型拖拉机”是什么有关。

二是条件多余。我们长期以来提供给学生的都是“封闭”的问题，这种问题的条件都用得上，都有唯一解法。这种“封闭”性具有深厚的文化背景。儒家文化的收敛性思维特征，数学史上“形式演绎”的强大作用，都使得“数学的开放式思维”在中国很难立足。[3]在教材编写上，体现为特别重视知识的逻辑性和严谨性，知识呈现情境简单且缺少开放性。问题都是结构良好的问题——条件不多不少，结果唯一。以至于学生产生这样的误解——每个问题都只有唯一正确的解答、唯一正确的解题方法，给出的每一个数都是条件，都要用上去。本案例中，学生将多余的“52”用于算式中可能就是这种思维惯性的作用。

从原文可知，案例中老师是在新接的班执教，对学生了解不够。这就好似闭着眼睛在崎岖的山道上行走，摔跤在所难免。

其次，理答失机变。

理答集中体现了教师的教学机智。好的设问可以是教师自己想出的，也可以是借用别人的;可以是自己瞬间想到的，也可以是自己长期冥思苦想出来的。面对老师的问题，学生会有千奇百怪的回答，不管教师如何预设，总有意料之外的情况出现，当各种情况出现时，教师如何随机应变，恰到好处地处理，体现了教师教学机智的程度。

案例中的教师从启发学生的良好愿望出发，却一步步走向了被动，除了叫答不见机的原因外，还在于他理答没能随机应变。

其一，当学生列出“52×150×12”这样的式子时，简单地认为“学生是在瞎猜”，而没有认识到问题主要出在学生不理解“XX牌52型拖拉机”指的是什么。由于教师没有捕捉到学生错误的真正原因，所以应对的办法就不对路子，只是随口追问了一句“你为什么这么列式？”当学生回答“我错了”时，老师又先入为主地认为：老师只要重复问一句，学生就习惯性地说自己错了，拿另一种计算方法来搪塞。其实，这种情形固然有学生猜的成分，但似乎也反映了学生具有的能听出话中之音的能力。再深而究之，是不是老师经常用这种问话方式来表示“你的回答不对”的信息，导致了学生这种习惯性认错呢？从学生的角度看，既然自己原来的回答错了，当然就应该换一种方法，这不是搪塞而是改进。

从有效帮助学生的角度看，当时老师应该紧扣“52×150×12”中不该出现的“52”进行启发点拨。应该认识到学生这样列式并不是没有任何道理，或许学生直观地认识到结果应该比已知的数都大，要用乘法;或许是因为记忆中类似的问题是用乘法，于是套用乘法;甚至学生可能觉得最近都是在学习乘法，所以这题可能也用乘法。可见，学生应该已经部分地感觉到应该用乘法的合理性，如果题中没有“52”这个数，那她就可能正确回答了。

其二，由于教师没能抓住问题的关键去启发点拨学生理解数量关系，学生思维仍处于模糊之中，所以猜罢了乘法又猜除法。面对这种情况，教师还是没能认识到对于这名学生的有效帮助应该是弄懂题意，分析数量关系。他想通过启发让学生自己发现错误，于是再次追问“怎么除”，以此来促进学生进行思考，进而否定除法。但是学生没有顺着老师的思路走，而是回答“大的除以小的”。这个回答也有理由，因为还没有学到小数除法，学生所见到的除法都是大的除小的。

既然启而不发，那教师只能直截了当地问“为什么是除呢”，这句话的内在意思是“除法是不对的”。学生听明白了，所以又承认错误。到了此时，教师应该认识到学生需要的是较为直接的帮助，然而他仍然希望学生能自己回答出正确的方法，再一次重复问“对的该是怎样呢”。学生根本就没有认识自己的错误到底是什么，更不知道正确的方法，所以只能再一次利用排除法，选择了加、减、乘、除四种运算中余下的加法。这虽然又是一种错误方法，但较之于减法来说还有一点思维含量的，毕竟加法的结果是变大，而减法的结果是变小，显然变大更有些道理。

其三，到了出现加法，教师终于知道要用举例的方法来帮助学生理解数量关系。他举了一个与问题的数量关系相同而情境更为贴近学生生活的问题——吃大饼，这是一种有效的启发方法。但是没想到学生受生活经验的影响，说“早上不吃大饼”。此时教师再一次不见机——没有认识到学生这话背后隐藏的“危险”，教学行为可能因此偏离数学的主题。果然，教师被学生牵偏了航向，问“那你吃什么？”其实，学生吃什么都可以，例子的核心作用是帮助学生理解数量关系，关系是核心，事物及其数量并不重要。

其四，当学生说“吃半个就可以了”的时候，教师应该敏锐地认识到，半个是0.5，这是小数，而小数乘法还没学到，这样的数据学生无法运用乘法来计算。所以应该及时地调整数据，而不能拘泥于学生的话。重视学生的生活经验，其目的是借以帮助学生进行理解和思考。必要时，要对生活经验作适当取舍、加工。由于此时不见机，其后果就是学生尽管正确回答了所举例子中的问题，但却对原题的解答没有裨益——学生是运用日常数学的思维方式解题的，具体而言是用累加的方式：“2天一个，5天两个半。”

二、学科教学知识（PCK）：教学机智的基础

1.PCK理论简介

美国学者苏尔曼（Shulman）在研究教师评价时发现，教师评价的测验内容存在只关注教学法的知识而忽视学科内容的现象。进一步地，教学法知识测试仅是涉及准备教案和评价、识别学生个别差异、教室管理与教育政策等，完全看不到学科的影子。由此认为，对学科内容知识的忽视已经形成当时教学研究领域中的“缺失范式”，必须强调将教师的学科知识与教学法的知识结合起来考虑，进而提出了“学科教学知识”（pedagogical content knowledge简称PCK）的概念。[4]所谓PCK就是教师将学科知识进行“心理学化”，使之成为学生易于理解的形态的知识，包括教师讲解某一主题所运用的可能的例子、解释、演示、举例与类比等方式，学生可能遇到的困难、错误理解，以适合儿童的思维与学习特点来重新表征学科知识。[5]学科教学知识体现了教师的专业独特性，是教师专业水平的衡量标志。

后继研究者格罗斯曼（Grossman）将学科教学知识分为四个要素：（1）教师对于任教某特定科目目的的信念;（2）了解学生学习某些主题的先前知识;（3）课程的知识，包括：横向课程（与各相关科目课程的联系）与纵向课程（了解学生所学过的与将学的事物）;（4）教师必须熟悉某些概念或主题最有效的教学与表征方式，并能在适当时机运用。[6]

2.PCK是教学机智的基础

借鉴格罗斯曼关于学科教学知识四要素划分理论，我们可以对案例中教师不能见机行事的原因作进一步的分析。

首先，从教师数学教学信念看。就小学数学教师而言，其教学信念系统包含五个主要成分：数学观、学生观、数学教学观、师生观以及数学教学效能感，[7]其中每一种成分都会对教师的教学行为产生影响。案例中的老师自始至终奉行这样一个原则——通过教师的启发，让学生自己发现错误，弄清原因，正确解答。在这种教学信念之下，教师处处以学生为主体，耐心接纳，尊重学生的每一个回答。面对一个个错误回答，教师不厌其烦地逐一进行追问，希望学生思维能够有所突破，获得成功。即使面临学生明显的胡猜乱答，不上路子的胡思乱想，也没有粗暴打断，否定呵斥。应该说，老师秉持了一个可贵的教学信念。问题在于，好的教学仅有好的信念还不够，还要有良好的洞察力和行动力，能洞察学生回答中隐藏的“机”，捕捉到教学中积极或消极的因素，因势利导，将教学引向良好的境地。从本案例具体情况看，教师面对学生多次的“旁枝斜出”，坚持启发的信念，迟迟不变换做法，最终形成“搞笑”的局面，学生也没能真正解决问题。可见教师的教学信念对教学行为有着强大的支配作用，但即使是良好的信念也需要机智的行动来实现。

其次，从教师关于学生的知识看。教师关于学生的知识包括三个维度：学生发展的知识（主要包括学生的心理发展、思维发展、已有的知识经验和学习疑难点等知识）、学生学习的认知因素与非认知因素知识（主要包括学习策略与方法、学习态度与能力、学习动机与风格等方面的知识）以及学习环境的知识（主要包括社会、政治、文化等外在大环境以及课堂学习的物理环境和心理环境等方面的知识）。[8]

案例中的老师由于新接的班级，所以对学生的整体和个体情况都不太熟悉，没有叫到合适的学生回答问题，这是可以理解的。他的问题在于以下三点：一是他设计的问题需要学生具有农村生活的背景知识，过于远离学生的生活经验，学生难以理解。二是他应该预见学生在回答有多余条件的问题时会出现困难。三是当学生列出“52×150×12”这样的式子时没有敏锐地认识到问题的关键是学生对“52”的不理解。

第三，从教师课程知识看。教师的课程知识包括：横向课程与纵向课程两个方面。前者主要指数学各知识领域之间的联系，后者主要指某一具体内容在教学编排顺序上的先后。显然，此案例中老师在纵向课程知识方面出了问题。因为当学生说每天吃半个粽子的时候，他没有敏锐地认识到这将涉及小数乘法的知识，这是整数乘法之后的学习内容。

第四，从数学教学知识方面看。教学知识主要包括教学目标、教学原则、教学内容、教学方法、教学评价、教学管理等方面。案例中老师熟练地运用中国教师惯用的启发方式——举例说明来启发学生。举例说明的实质是利用一个与目标问题结构相同、相似或相近，而难度较小或较为贴近学生生活经验，易于成功解答的问题来作为一种铺垫，通过铺垫题的成功解答从而获得有益的启发，进而解决目标问题。当学生解题连续两次失败后，老师举了一个吃大饼的例子，这个例子与原问题结构相似——具有相同的数量关系“单一量×份数=总量”，而且非常贴近学生生活实际，学生在生活经验支持下容易加以解决。问题在于教师拘泥于例子的“真”而对其“假”的属性认识不足，一味顺着学生的实际走，最终偏离举例说明的初衷。这背后其实是教师对日常数学特点和价值认识的欠缺。

日常数学作为数学知识的一种形态，广泛存在于学校场景之外和教学起始之前，并在人们解决日常生活问题的过程中发挥着积极作用。但是，日常数学也具有局限性，它不是运用简约、抽象的符号进行形式表征，而是运用日常经验、有形物体、直观图形进行外部表征。而且它是离散的、零碎的，缺乏良好的系统性和统一的结构性。所以，它对具体情境有着较强的依赖性和附属性，往往不能脱离具体的情境。在面对大数量和逆运算时往往失去了效用，很难实现从一个情境到另一个情境的有效迁移。[9]

综上所述，我们可以得出这样的结论：全面而深刻理解的学科教学知识（PCK）是教师教学机智生成的前提条件，教学机智是教师根据现场的实际情况灵活辩证地运用学科教学知识的结果。

三、理论探索：教学机智的生成

教师的学科教学知识（PCK）是其教学机智生成的必要条件而非充分条件，从学科教学知识到教学机智要经历复杂的“化学变化”。概括地说，要经过两个变化阶段。

1.从学科教学知识（PCK）到学科教学能力（PCA）

静态地看，小学数学教师的学科教学知识是一种陈述性知识。这有利于揭示出学科教学知识的构成，但同时也会陷入一种误区——仅将其视为一些僵化的原则和条款，忽略其在具体教学情境中的生成性、灵活性特征，因此有必要从动态的视角对其进行分析。

动态视角下的学科教学知识是一种程序性知识，其实质是一种教学能力。据此，喻平提出学科教学能力（pedagogical content ability简称PCA）概念。[10]所谓教师的PCA，是指教师在教学过程中，根据特定的教学内容、特定的学生群体、特定的教学环境，在自身认识信念的支持下，在自我监控的作用下，从自己的基本知识结构中选取、组合、贯通相关知识，用于设计教学进程和解决教学操作中出现的问题的能力。

教师的学科教学能力作为知识看待就是程序性知识，由教师的陈述性知识转化而来，是在知道“是什么”的前提下走向知道“怎么做”，表现出面对具体教学情境，教师综合利用知识结构的动态过程。从内在表征来看，它是一个产生式系统，教师在拥有相关知识的基础上，头脑中形成的一系列“如果…那么…”。一条“如果…那么…”即一条产生式，因为教学事件是复杂多变的，出现一个“如果”可能会用多个“那么”应对，也可能出现一个“那么”会有多个“如果”应对的情况，因此，教师的学科教学能力的内在表征是一个复杂的产生式系统，其运行过程就是一个逻辑推理过程。

2.从学科教学能力（PCA）到教学机智

学科教学能力作为一种能力，是教师的一种内在素养，通过具体的教学行为体现出来。教师的课堂教学行为其实是教师面对具体情境所作的一系列“如果…那么…”的推理，这种推理一方面基于教师对数学知识、学生知识和教学知识等知识的深刻理解和掌握，另一方面也受控于自己的信念系统，其中的每一种因素都会对行为产生影响。

教师课堂上的行为从本质上来说具有合规律性和合目的性特征，即一方面要符合逻辑推演的规则，又要服务于一定的教学目标。尽管教师在主观上想达成行为的合规律性和合目的性，但其行动的客观效果却可能大相径庭：可能是一般招数，也可能是妙招，甚至是昏招。妙招契合着知识逻辑，但仅凭知识逻辑却不一定能得到，只有在“灵光闪现”——“顿悟”的情况下才能出现。

冯契的“转识成智”哲学理论认为，“顿悟”需要三个条件：理性自知、意志自主和情感自得。[11]理性自知即教师拥有丰富的知识且对其有深刻的理解，这是教学机智产生的基础条件。意志自主即教师要树立正确的宇宙人生态度，摆脱各种羁绊达到自由的境界。具体而言就是树立良好的世界观、人生观、知识观、价值观，乃至于学生观、教学观和课程观等观念。以此正确的观念去调适、监控自己的教学思想和行动的方向;情感自得就是教师在情感上要净化灵魂，树立大爱，关心学生，热爱教育事业。以高尚的师德和师爱去评价、浸润和提升自己的思想和行动。如此，学科教学知识才能经由顿悟转化为智慧，达到“无不通也，无不由也”的境界。此时，教师具有敏锐感受、准确判断生成和变动过程中可能出现的新情势和新问题的能力;具有把握教学时机、转化教学矛盾和冲突的机智;具有根据对象实际和面临的情境及时做出决策和选择、调节教学行为的魄力;具有使学生积极投入学习生活，热爱学习和创造，愿意与他人进行心灵对话的魅力。教师的教学因此而进入到科学和艺术结合的境界，充分展现出个性的独特风格。教学于教师而言，不仅是一种工作，也是一种享受。[12]

3.教学机智生成模型

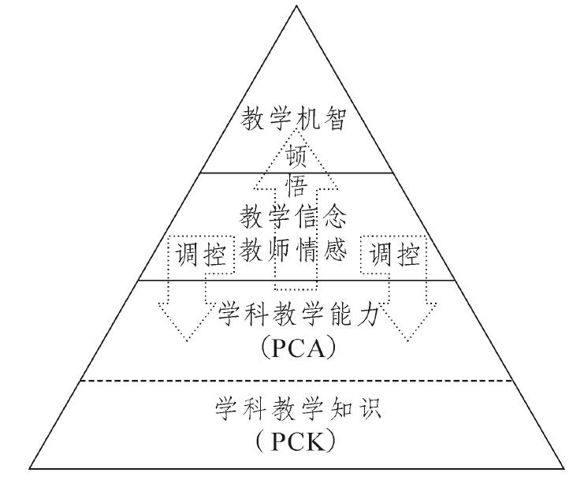
根据以上分析，我们可以将教师在学科教学知识的基础上生成教学机智的机理描述成下图：

教师静态的学科教学知识（PCK）转化为动态的学科教学能力（PCA），两者在情感和信念系统的调控下经由顿悟而生成教学机智。教学机智是教师在理性自知、意志自主和情感自得状态下实现的，它遵循理性精神又超越理性，是教师知识、信念和情感熔铸而成的合金。它是一种实现的状态，潜隐于大脑中的思想无论如何奇妙，都不能称为机智，实践性是它的本质特征。

参考文献：

[1]郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，2008：16.

[2]古汉语常用字字典（修订版）[K].北京：商务印书馆，1993：130.

[3]戴再平.开放题——数学教学的新模式[M].上海：上海教育出版社，2004：1-2.

[4]Shulman，L. Those who understand： Knowledge growth in teaching[J]. Educational Researcher，1986，15（7）：4-15.

[5]Shulman，L. S. Knowledge and teaching： Foundations of the new reform[J]. Harvard Educational Review，1987（57）：1-22.

[6]Grossman P. L. The Making of a Teacher： Teacher Knowledge and Teacher Education[M]. New York： Teachers College Press， 1990.

[7]杨豫晖.教师教学信念的检视与反思——以小学数学教师为例[J].课程·教材·教法，2010（12）.

[8]李渺，宁连华.数学教学内容知识（MPCK）的构成成分表现形式及其意义[J].数学教育学报，2011（4）.

[9]罗新兵，罗增儒.关联日常数学与学校数学[J].数学教育学报，2005（5）.

[10]喻平.数学教学的三种水平及其理论分析[J].课程·教材·教法，2012（1）.

[11]冯契.冯契文集（第一卷）·认识世界和认识自己[M].上海：华东师范大学出版社，1996：42.

[12]叶澜.新世纪教师专业素养初探[M].北京：教育科学出版社，2001：26.

责任编辑：丁伟红

Teaching Intelligence and Pedagogical Content Knowledge： Case Analysis

WANG Jiu-hong

（Nanjing Tianzheng Primary School， Nanjing 210037， China）

Abstract： Students behaviors in classroom have their own rationality， which requires teachers to handle with teaching intelligence. The precondition for teachers to generate teaching intelligence is to fully and deeply digest pedagogical content knowledge （PCK）， which dynamically takes the form of pedagogical content ability （PCA） which could be changed into teaching intelligence through insight under the monitoring and adjusting of emotional and belief systems.

Keywords： teaching intelligence; PCK; PCA; insight