挖掘机回转减速机运动学及动力学仿真

张凡凡 罗艳蕾

摘 要：以某挖掘机回转减速机为研究对象，通过UG建立减速机的三维模型，将模型导入到ADAMS中建立减速机的虚拟样机，再对虚拟样机进行运动学与动力学仿真，得到各级转速、齿轮啮合力等曲线。将仿真结果与理论计算进行对比，证明虚拟样机建立正确，也为减速机动态特性优化提供一定的指导。

关键词：UG;行星减速;ADAMS;动力学仿真

引言

行星减速机具有结构紧凑、传递速度范围大、运行平稳等优点，被广泛地应用于建筑、冶金等领域。由于其结构相对复杂，使用传统方法不易对其动力学特性进行精确计算，也无法准确预测其工作性能。本文在ADAMS中建立虚拟样机，可得到所需的各种数据曲线。为零件的强度校核、寿命预测和工程设计等提供支持。

1.行星减速机的工作原理

本文研究的行星减速机采用2级行星轮系组成，每一级结构都采用NGW型传动。如图1是此行星减速机的传动结构简图。

此减速机属于周转轮系[1]，由于内齿圈

固定不动，所以=0（m，n，H分别代表太阳轮、内齿圈、行星架），所以减速比：

即：

得出n级NGW型的减速比

各级太阳轮齿数各级内齿圈齿数

图1.二级行星减速机结构简图

1.一级太阳轮 2.一级行星轮3.一级行星架

4.二级太阳轮 5.二级行星轮6.二级行星架

7.内齿圈

本文的减速机一级太阳轮、一级行星轮、内齿圈、二级太阳轮、二级行星轮的齿数分别为：21、33、87、21、23。所以总减速比为（1+87/21）2=26.45。

2.减速机三维模型的建立

由于ADAMS不善用于复杂3D曲面的三维建模，所以采用UG来建立三维模型。

2.1齿轮和花键的参数化建模[2]

变位齿轮用传统的建模方法可能建模失败，因此采用参数化建模齿轮和花键。在UG工具菜单的表达式命令中输入齿轮的渐开线方程，然后在“插入”下拉菜单中的“规律曲线”下“通过方程”生成具体的渐开线，再镜像此渐开线，随后作出该齿轮的齿顶圆和齿根圆，最后进修修剪、拉伸圆形阵列等操作即可完成齿轮三位建模。

图2.产生的渐开线和一个齿轮

2.2其它零部件的三维建模

其它零件采用传统的建模方法。即在UG中“插入”→“草图”→“拉伸/旋转/扫掠/布尔运算”等步骤来完成零部件的建摸。

2.3行星减速机的虚拟装配

模型装配可以按照实际的物理装配顺序进行装配，运用适当的约束关系使最后的总装配体符合实际的物理样机。

图3.减速机的总装配体

3.行星减速机虚拟样机的建立

3.1模型导入到ADAMS中

将UG中的模型导出为Parasolid中的.xt格式，然后才能导入到ADAMS中。

3.2在ADAMS中材料属性的定义

导入ADAMS后首先定义零件的材料属性。太阳轮和行星轮为20GrMnMo，内齿圈和行星架为40Gr。20GrMnMo/40Gr对应的泊松比、杨氏模量、密度属性分别为0.3/0.28、207GPa、7800/7100 kg/m3。

3.3在ADAMS中添加约束

在ADAMS中给各个零件添加相应的旋转副、固定副等约束。

3.4在ADAMS中的啮合齿轮之间定义接触

本文将要定义13个接触，只要是相互啮合的齿轮对之间，不论是内啮合或外啮合，都定义一个接触。

3.5在ADAMS中接触力的选择和定义

ADAMS中选用冲击函数法计算接触力，接触力由相互切入产生的弹性力和相对速度产生的阻尼力组成[3]。冲击函数等于

（1）

其中—两个物体的实际距离;—两个物体的参考距离;—接触刚度;—指数—阻尼。所以用冲击函数法，需要确定指数、切入深度、接触刚度和阻尼。

3.6在ADAMS中接触力的相关参数确定[4]

指数：对于金属材料，e的取值为1.3到1.5，故e=1.5。

切入深度：通常情况下，在没有指定穿透深度时，应尽量取较小值，本文取穿透深度x=0.01mm。

接触刚度（Stiffness ）：取决撞击物体的材料和结构形状。根据Hertz静力弹性接触理论：，由此式得到碰撞时法相接触力和变形的关系为：。刚度系数= ，其中=，=，而为材料的弹性模量，和为材料的泊松比，和为物体在接触点的接触半径，由于齿轮的齿高和分度圆半径变动范围不大，可用分度圆半径来替代[3]。由参考文献5，刚度系数，由参考文献6知：

图表4.啮合刚度系数值

阻尼：阻尼系数的值正常取刚度系数的1/1000-1/100倍之间，因此取=1000。

滑动摩擦力计算方法选库伦法，设置静态系数=0.08、动态系数=0.05。

4.行星减速机的运动学与动力学仿真

进行仿真运行前，还需添加运动激励和负载转矩，及设置仿真运行参数。

4.1在ADAMS中添加运动激励及负载转矩

为了运动时，速度不产生较大突变，采用Step函数。Step（time，0，0，0.2，9828d）使角速度在0.2秒内从0增加到9828度/秒。

在输出轴上施加-4000Nm的力矩，同样定义step（time，0，0，0.2，-4000000）。

4.2设置仿真时间、步长及积分格式

设置仿真时间2秒，步长0.0001。采用GSTIFF积分器下SI2积分格式替代默认的I3积分格式。

图5.ADAMS中搭建的虚拟样机

4.3减速比验证

图6.一级太阳轮、行星架和二级行星架的角速度

如图6，一级太阳轮的角速度是在0到0.2秒内逐渐增加到9828度/秒，然后保持匀速。一级行星架的角速度在1910度/秒上下波动。二级行星架370度/秒上下波动。与理论值比较验证了虚拟样机的正确性。

4.4同级行星轮的接触力的对比

图7.三个二级行星轮与内齿圈的接触合力放大图

如图7，三个二级行星轮与内齿圈的三个接触力都在15000N左右波动，三个力的波动范围略有差别，但差别不大，表明均载状况良好。

4.5齿轮接触力分析

图8.一级太阳轮与某一同级行星轮在X、Y和Z方向的接触力

由于是直齿轮传动，所以X和Y方向有接触力，Z方向没有接触力。由于行星传动是非定轴传动，行星齿轮不但绕行星轴自转，也随着行星架公转，因此，X和Y方向啮合力呈谐波性（如图8）。

图9.一级太阳轮与一级行星轮的接触合力

图10.一级行星轮与内齿圈的接触合力

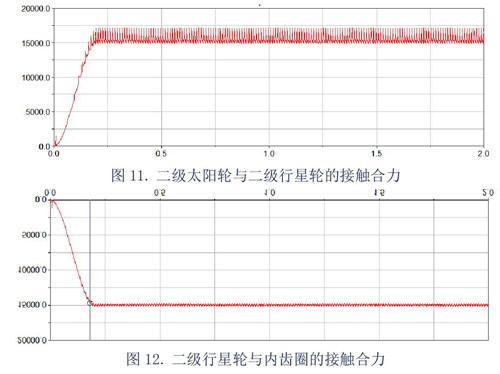
图11.二级太阳轮与二级行星轮的接触合力

图12.二级行星轮与内齿圈的接触合力

理论上同级的每个太阳轮和行星轮、行星轮和内齿圈的法相接触力应相等，均为：，T为转矩，N为同级的行星轮个数，i为本级的减速比，R为太阳轮分度圆半径。

如图9、10、11和12，每一级太阳轮与行星轮的啮合力略大于行星轮与内齿圈的接触力。考虑到偏载和摩擦力的存在，此情形与实际相符。高速速级齿轮间的接触力波动幅值较大，而对应的低速级齿轮间的接触力波动幅值较小，这说明构件转速在低速下，有利于减小工作时的动载荷。

结论：

（1）渐开线齿轮动态啮合力的仿真分析方法可准确的计算齿轮传动的动态接触力。

（2）仿真结果表明：齿轮传动的速度越大，动载荷越大。

参考文献：

[1]孙恒，陈作模，葛文杰.机械原理[M] 北京：高等教育出版社，2006年5月

[2]麓山科技.UG NX8中文版零件设计实例精讲[D].机械工业出版社，2012年4月

[3]李增刚.ADAMS入门详解与实例[M].北京：国防工业出版社，2006年4月

[4]渐开线齿轮啮合碰撞力仿真[ J ]. 中南大学学报，2011， 42 （2） ： 379 - 383.

[5]姜振波.机器人用RV减速器动力学性能分析[D].大连交通大学，2010年12月

[6]何卫东，李力行，李军.机器人用RV传动中摆线轮受力分析[J].大连铁道学院学报，1999年6月 第20卷 第2期：50-53

项目基金：国家科技支撑计划（2013BAF07B01）

作者简介：张凡凡（1989—），男，汉族，江苏响水人，硕士，主要从事液压传动与控制方面的研究。