集合材料在音乐中的结构关系

廖轲

【摘要】作为二十世纪最重要的作曲家之一，勋伯格打破了传统音乐的调性束缚，促进了无调性音乐的发展，他的钢琴代表作之一《钢琴小品六首》也被后人作为无调性的代表作品而广泛分析与研究。本文就以《钢琴小品六首》op.19no.3为例，运用集合理论进行音乐材料的结构分析，从而探索出集合材料在该音乐作品中的内在结构关系，并发掘出其在如何推动音乐的发展中所起到的重要地位。

【关键词】音级集合；截断；集合材料；结构关系

引言

奥地利作曲家、理论家和音乐教育家阿诺德·勋伯格（ArnoldSchoenberg）是二十世纪以来最具影响力的一位音乐大师，其对当代音乐的贡献使得他在音乐史上占有着重要的位置。占有重要地位的传统调性音乐统治着音乐界长达几个世纪之久。然而这一情形被勋伯格最早打破，他摆脱了传统调性音乐的束缚并开启了无调性音乐时期，后来经过不断了探索，他创造性的提出了十二音序列音乐写作的模式，并以此为理论依据创作了大量音乐作品。然而从调性音乐剑无调性音乐的发展，这个改变的过程并非一帆风顺，在这个过程巾，勋伯格不断的打破传统音乐的理论束缚，不仪在和声上还是在曲式结构等方面，可以说勋伯格完全是在颠覆传统音乐的理论理念。但经过不断的摸索，勋伯格最终找到r适合自己的一套音乐体系，他的努力也成功的使他在音乐史上占有一席之地，为音乐理论的发展做出r巨大的贡献。《钢琴小品六首》op.19则是勋伯格的代表作品之一，而本文分析的是其中第二首，分析的方法采用的是音级集合理论，运用这一理论可以发掘音乐内在的结构关系，从而更为客观的分析出音乐的材料运用和音乐的整体与细微之问的联系。集合理论作为现代音乐的一种分析手段，最早由美国理论家弥尔顿·巴比特（Milton Bahhitt）提出，在二十世纪初开始形成，经过艾伦·福特（Allen Forte）的总结发展，渐渐成为了一套较为全面的理论体系，不过集合理论的发展远未停止，许多音乐理论家不断探索和研究，丰富着集合理论体系。

一、《钢琴小品六首》op.19 no.2的集合材料

用集合的方法分析作品结构，第一步首先要划分出音乐作品的材料结构块，即集合理论中所说的截断，从该作品的旋律线以及音乐段落的结构上看，我们可以划分出8个截段材料。然后把这8个截断材料从整首作品巾分离并依序表示出来，如图1所示。

二、各截断的集合

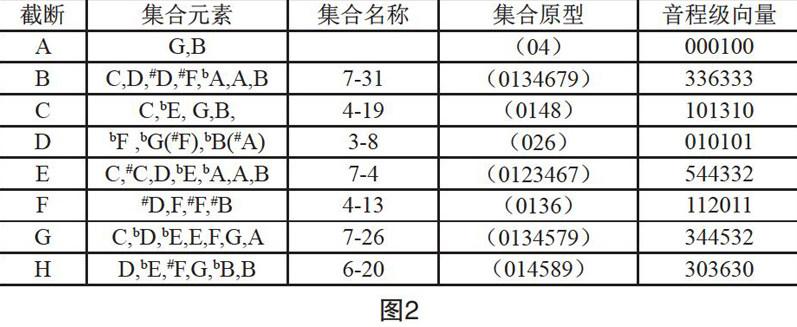
通过把各个截断从整首作品中截取出来，我们便得到了类似于乐汇般的诸多音乐材料片段，这些片段及其一些发展和变化共同构成了这首完整的作品。接下来我们便是需要探寻这些截断材料其本身的内涵与相互之问的内在关系。运用集合理论与集合族列表，能够得到每个截断具体的集合，如图2所示。

三、各截断在音乐整体中的结构关系

透过上面的截断集合列表，我们能够了解每个截断的集合内容，包括集合原型以及音程级向量等。把所有截断都截取出来后我们能够观察每个截断的自身关系与特点，但在分析的过程巾每个材料都不是单独存在的，通过每个材料与全曲之问关系的分析和每个材料相互之问的关系的分析，才能使我们对于整部作品的结构框架以及音乐表现的内容有所了解，首先是把截断还原于乐曲本来的位置进行解释分析。

乐曲的一开始出现的是截断A的集合内容，截断A是一个双音级合，由于在艾伦·福特的集合表里标记出的最小集合为二音级合，因此，截断A的双音级合并没有集合名称（也称为福特名）。但是按照音程级向量的计算方式依然可以将双音级合的音程级向量算出，纵观全曲，音乐的发展基于截断A中的双音级合，一直到乐曲结束；截断B是一个七音级合，连音线使得这几个音成划分为—个整体，这个截断的音乐形态在全曲中是一个具有旋律特线征的集合；截断C是四音级合，是包含截断A中双音级合元素的一个发展；截断D是由—个三音和弦和一个双音组成，按照等音相同的概念，这两个和弦中有两对音组的集合元素相同，因此截断D是—个四音级合；截断E是由四组三度关系的双音组成的一个七音级合；截断F为一个有延留的七音柱式和弦结构的四音级合；截断G与截断E相似，由五组三度关系的双音组成，与截断E不同之处在于节奏与音符时值的不同；截断H同样为一个七音柱式和弦结构的四音级合再加上截断G最后一个双音的延留，共同组成了一个六音级合并全曲结束，截断H相当于一个终止和弦的作用。

四、各截断之间的结构关系

（一）截断A与截断C的关系

我们知道截断A是一个双音级合，包含G，B两个集合元素；而截断C是个四音级合，包含有C，bE，G，B四个集合元素，显而易见的，截断A的元素包含于截断C中，因此它们属于子集与母集的包含关系，即截断A是截断C的具象子集。

（二）截断D与截断E的关系

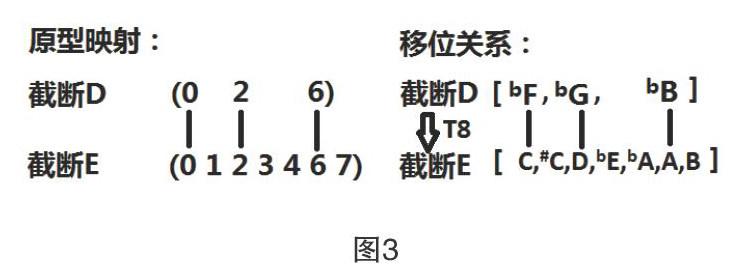
截断D与截断E的关系比较隐性，从集合元素上看，截断D包含bF，bG（#F），bB（#A）三个集合元素，截断E包含c，#C，D，bE，bA，A，B七个集合元素，从元素上看，两者似乎无什么关系，但是把两个截断进行原型表示后我们会发现截断D为3-8：（026）；截断E为7-4：（0123467）。从原型上我们可以看到，截断D是映射于截断E的原型的，这表示截断D其实是截断E的抽象子集，需要进行移位的操作才会在集合元素上一一映射，移位关系如图3所示。

（三）截断B、截断E与截断G的关系

同样作为七音级合的三个截断，它们之间的关系是值得比较的，而通过观察后会发现，这三个截断无论在集合元素上还是在集合原型上都没有什么联系，那么它们之间到底什么关系呢？这就需要我们观察其音程级向量了，观察音程级向量是为了比较集合间的相似性关系，因此我们需要通过比较音程级向量来确定三者的关系是最大相似性还是最小相似性。比对过后我们呢会发现，截断B与截断E、G为最小相似性关系，截断E与截断c为最大相似性关系，如图4所示。

（四）截断C、截断F与截断H的关系

截断c与截断F都是四音级合，而截断H为六音级合，但是仔细观察截断H会发现，它是由截断G最后的双音和一个四音和弦共同组成的这个六音级合。其组成关系如图5所示。

因此我们可以在截断H中得到一个新的四音级合4-19：（0148）。音程级向量为：101310-这个四音级合可以看做截断H中六音级合的具象子集。这时对比这三个截断便会发现，这个新的四音级合与截断C的集合原型相同，二者互为移位关系。而截断C、截断H与截断F互为最小相似性关系，如图6所示。

五、结语

通过运用集合理论对音乐细节的分析，片段与整体，片段与片段之间的分析等，能够对整首音乐作品在材料结构上有一个清晰的认识，这也是集合理论作为一种无词性音乐分析手法所展现的功能与作用。在分析这首作品方面，我们能够看到各集合截断所表现的内涵与音乐之间的联系，包括集合的包含关系、移位关系以及相似性关系等，使得我们能够总结出这部作品在音乐材料的运用方面，不仅有发展还有对比，音乐语言比较丰富，整个音乐的结构和材料之间的联系却十分密切。不可否认这虽然是一首规模小巧的钢琴小品，但是简单的集合材料背后却有着严密的逻辑关系，结构不紧不松，精炼新颖。