一种新的MIMO—OFDM信道估计的低复杂度设计方法

徐永键　戴建强　齐立成　谭洪舟

【摘 要】针对多输入多输出-正交频分复用（MIMO-OFDM）系统信道估计导频损耗和算法复杂度问题，提出了一种低复杂度的MIMO-LS算法设计方案，它要求每根发射天线中的导频序列为等间隔排列，而不同天线间的导频序列相互相移正交。当在OFDM导频符号中选取一个合适的导频间隔时，对比传统的最优导频设计方法，提出的MIMO-LS算法在基于最小均方误差-峰值平均功率比（MSE-PAPR）双准则的前提下，最大程度降低导频损耗和算法复杂度。计算机仿真验证了此算法的有效性。

【关键词】MIMO-LS信道估计；复杂度；最小均方误差-峰值平均功率比双准则

0 引言

MIMO-OFDM 技术是多入多出（MIMO， multiple input multiple output）技术与正交频分复用（OFDM， orthogonal frequency division multiplexing）技术的联合，由于该技术能够在有限的带宽内实现更高速率、更可靠的传输[1]，因而MIMO-OFDM被选为下一代无线通信系统的核心技术。在MIMO-OFDM系统接收端，信道估计器是一个重要的部分，它直接影响接收信号的质量和系统的性能，所以设计一个适用于MIMO-OFDM系统的低复杂度、易于实现的信道估计器对研究实现MIMO-OFDM无线通信系统有十分重要的意义。

基于导频辅助的最小二乘法LS信道估计算法简单易于实现，在实际中获得较多的应用。但是，由于它对噪声干扰以及频率同步误差很敏感，所以LS信道估计的准确性会降低很多。2003年，I. Barhumi[2]提出最优导频设计，可以使MIMO系统的LS信道估计达到最好的MSE性能，但是，没有考虑到MIMO-OFDM系统的峰均比（Peak to Average Power Ratio， PAPR）问题，这对系统性能会造成很大的影响，此外也没有综合考虑到多天线时的复杂度和导频损耗问题，不同天线导频序列之间的相互干扰也没有被考虑进去。

为了设计一个低复杂度的信道估计方法，本文综合考虑MSE和PAPR，导频损耗和算法复杂度，通过联合均方误差最小和导频矩阵的峰均比最优双准则设计出最优导频，并在OFDM导频符号中选取一个合适的导频间隔，从而给出低复杂度的MIMO-LS方法，使系统的MSE性能和PAPR性能均较优。仿真实验验证了此方案的有效性。

1 MIMO-OFDM系统LS信道估计

MIMO-OFDM系统框图如图1所示：

图1 MIMO-OFDM系统框图

系统主要由发送端、无线信道、和接收端三部分组成，X1，X2为发送序列，经过OFDM调制后，经多天线发射，经过无线信道后，在接收端进行解调，信道估计和均衡。MIMO-OFDM系统数学模型可表示为

Y=XH+W（1）

其中H为待估计参量矢量，X为已知的发送数据，Y为观测值的矢量，W是均值为0、方差为σ2的高斯白噪声矢量。假设系统信道是广义平稳非相关散射的信道。由于在接收端，每一个接收天线上的接收信号都是来自所有发射天线上信号的叠加，为方便表示，下文将表示不同接收天线的下标j在Hij，Hj和Wj中都省略了。

在MIMO-OFDM系统中，当接收机已知导频信息时，利用LS准则可以得到信道的估计参数。设Xp为导频矩阵，从式（1）可得

Yp=XpFh+W（2）

其中F是定义的DFT酉矩阵，根据式（1），式（2）可得，h的估计值为

可以通过导频设计将Dij简化成对角阵，避免对大矩阵做求逆运算，以降低MIMO系统LS信道估计的复杂度。

2 MSE-PAPR双准则最优导频信道估计

2.1 最优导频设计及MSE-PAPR分析

将式（5）中AHA写成Nt×Nt个子矩阵：

令不同导频序列相互相移正交[4]，即当i不等于j时Xi*Xj=0，带入式（10）可得Dij=0。当i等于j时，令各个频点的能量相等，则XpXp*=K/P，其中K为一个导频序列的能量，P为每个OFDM符号导频数。

综上可得，AHA。代入式（5）可以得到 MIMO系统LS信道估计的最小均方误差：

所设计的最优导频除了关系到MSE外，还与PAPR有关。按照以上对能量和导频相互关系的设定，可以将第Ni个发射天线的最优导频序列表示

其中Ni={1，2，…，Nt}，SNi=p={0，1，…，P-1}，比如将天线1和天线Ni的导频序列设计为相移关系，由式（12）可得他们的关系为

令式（12）中Ni=1，S1=0，可以得到第一条天线上的一组最优导频序列为

式（14）经过IDFT变换到时域后，与最优导频序列对应的时域信号是

其中，TN为OFDM符号周期。根据峰均比定义[5]，可得第一根天线上发射的最优导频序列的峰均比为

若在时域上保持OFDM符号总数NumOFDM不变，将OFDM导频符号间隔扩大g倍，即将OFDM符号周期TN扩大g倍，则式（15）可变为

则第一根天线上发射的最优导频序列的峰均比为

PAPR=TN（18）

由式（16）和式（18）容易看到，OFDM导频序列的峰均比变大了g倍。按式（13）设计第Ni根发射天线上的最优导频序列为第一根发射天线上最优导频序列的相移，同样可得其他发射天线的峰均比为gTN。

2.2 MIMO-LS信道估计

按MSE和PAPR双准则设计了最优导频矩阵后，下面具体介绍使用最优导频做信道估计的方法，本文称其为 MIMO-LS信道估计。其中迭代信道估计过程如图2所示。

图2 迭代信道估计数据处理示意图

首先将经过OFDM解调的数据送入数据分离单元，数据分离单元在准确时间同步的前提下，将输入信号分离，输出两路信号，一路为OFDM块状导频符号，另一路为OFDM数据符号，然后将OFDM块状导频符号送入迭代估计单元进行首次信道估计，接着将估计得到的信道响应值用于对紧邻的OFDM数据符号的信道响应值进行估计，提取出第一个OFDM数据符号的信道估计值，送入迭代估计单元用于估计其紧邻的下一个OFDM数据符号所在时间点的信道响应值，直到下一个OFDM导频符号处，进行校正后重新开始下一个周期的估计，最后输出有效数据和信道估计结果，用于下一级信道均衡。

在MIMO系统的接收端用改进的MIMO-LS法估计，采用上节得到的最优导频序列，如式（13）所示，将多天线的各个导频序列ti[n，k]设计为相移关系。假设因此，新的MIMO-LS算法可避免对多维矩阵求逆运算，和传统的LS算法相比，大大降低了计算复杂度，且有更大的SNR适用范围。

2.3 最优导频间隔

周期性在时域插入最优导频OFDM符号，在所有载波上插入导频，所设计的导频间隔相等，各个天线的导频结构相等。这样就得到了等间隔、等功率、相互正交的最优导频矩阵。为了不失真的还原时域信号，插入导频的间隔必须满足奈奎斯特抽样定理，在实际OFDM系统中，所插入导频符号在频率方向上的最小间隔Df满足：

由式（23）可知，当其他条件一样时，导频间隔越小，带来的导频损耗越大，系统有有效数据传输速率就越低。定义信噪比损失[7]为

V=10log10（1/（1-？撰））（24）

由式（24）可知，当其他条件一样时，导频损耗越大，信噪比损失越大，从而系统容量会减小。此外具体信道环境参数也会影响导频开销。

从MSE和PAPR准则方面考虑，导频间隔越小，MSE越小，PAPR越小，则对应的OFDM导频符号的PAPR越小，系统的PAPR越小，但当天线数增加时会增大。如果通过增加OFDM符号导频数，就可以降低导频PAPR，从而降低系统PAPR。所以根据MSE-PAPR双准则和导频损耗可得出一个合适的最优导频间隔。

3 仿真结果

搭建一个2×2的MIMO-OFDM系统，在发送端设计好最优导频序列Xp，插入导频后形成输入数据X1和X2，信号经过编码和映射调制后，串并变换到发射天线1和发射天线2；然后通过无线MIMO信道，在接收端使用信道估计得到信道信息，再通过均衡模块，解调解码后得到原比特流。

为方便计算分析，令X2=X1。图3给出了在不同信噪比下，导频间隔为8的情况下MIMO-LS方法，和传统MIMO-OFDM系统时域LS信道估计的MSE仿真对比。从图3中可知，相比于传统的最优导频方法，MIMO-LS的MSE略小。这是由于本文所采用的导频数要比传统的最优导频设计方法多，因而导频能量更大，插值带来的误差更小，信道估计的精度更高。

图3 信道估计MSE性能对比

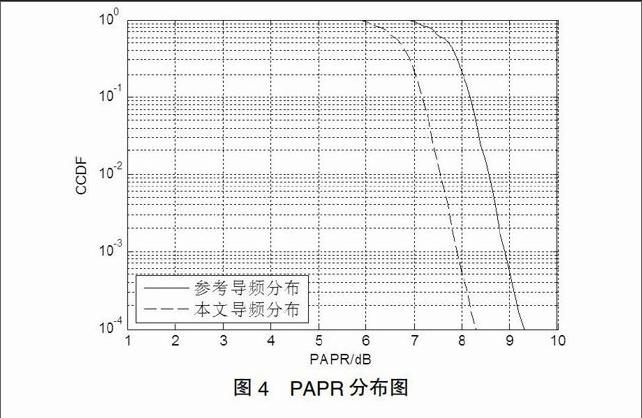
图4给出了MIMO-OFDM系统MIMO-LS方法下和传统LS信道估计方法下，其OFDM导频符号部分的PAPR仿真对比。用互补累积分布函数CCDF来描述PAPR的特性，其表示PAPR超过某一门限值的概率。从中可以看出，采用本文的导频分布能获得优于采用传统导频分布的PAPR性能，论证了本文所设计导频的有效性。（下转第11页）

图4 PAPR分布图

4 结语

本文主要讨论了MIMO-OFDM系统LS信道估计问题，给出了一种低复杂度设计方案，它要求每根发射天线中的导频序列等间隔排列，不同发射天线中的导频序列相互相移正交，进而给出了基于最优导频设计的MIMO-LS信道估计方法。讨论中我们发现，最优导频序列在时域上的导频间隔扩大倍数越小，其峰均比则越低，MSE性能越好，但是导频损耗越大，有效传输速率越小。对比传统的最优导频设计方法，本文提出的方案所允许的频带损耗更少，带宽更大，仿真试验验证了此算法的有效性。

【参考文献】

[1]周慧强，周世东，王京.MIMO-OFDM系统的时域导频信道估计算法[J].清华大学学报，2005，45（10）：1353-1355.

[2]I .BARHUMI， G. LEUS， M. MOONEN. Optimal Training Design for MIMO-OFDM Systems in Mobile Wireless Channels[J].IEEE Trans.Signal Processing， 2003，51（6）：1615-1624.

[3]B. Song， L. Gui， W. Zhang. Comb type pilot aided channel estimation in OFDM systems with transmit diversity[J]. IEEE Transactions on Broadcast， 2006，52（6）：50-57.

[4]王晗，汪晋宽.一种MIMO-OFDM系统信道估计中的最优导频设计改进算法[J].系统仿真学报，2009，21（5）：515-517.

[5]J H MANTON. Optimal Training Sequences and Pilot Tones for OFDM Systems [J]. IEEE Commun，2001，5（4）：151-153.

[6]汪敏，胡泽，肖斌.MIMO-OFDM系统信道估计中的最优导频设计[J].通信技术，2010，43（6）：20-23.

[7]HSIEH M，WEI C. Channel Estimation for OFDM Systems Basedon Comb-type Pilot Arrangement in Frequency Selective Fading Channels[J].IEEE Trans on Consumer Electronics，1998，44（1）：217-225.

[责任编辑：汤静]