基于MCMC的数字岩心重建方法

张思勤，汪志明，王小秋，李江涛，洪 凯

(中国石油大学(北京) 石油工程学院，北京 102249)

基于MCMC的数字岩心重建方法

张思勤，汪志明，王小秋，李江涛，洪 凯

(中国石油大学(北京) 石油工程学院，北京 102249)

常规的多孔介质重建方法主要考虑基质和孔隙两部分，而且编程难度大，计算速度慢。针对页岩气储层各向异性且含有有机质的特点，提出了一种基于改进后的马尔科夫链-蒙特卡洛(MCMC)方法的数字岩心重建方法：先从实际页岩气储层二维切片图像中提取孔隙度和有机质，分别重建孔隙和有机质的数字岩心，再将孔隙和有机质的初始模型组合在一起构成最终的页岩气储层数字岩心。研究结果表明：通过对比分析二维MCMC重建图像和原图自相关函数，发现该方法重建图像能够较好反映原图性质；该方法计算速度快，过程简单，方法所重建的模型能够较好体现页岩储层各向异性的特点且能反映页岩储层含有有机质的特性。

页岩气储层； 马尔科夫链-蒙特卡洛；数字岩心；组合模型

多孔介质结构复杂，普遍存在于自然界中，因此，对于多孔介质的研究具有广泛的工程意义，如煤层气的开采、页岩气的开发等。在宏观渗流中，一般应用达西定律来描述流体运动特征，由达西定律得到的宏观参数只能用来表征流体运动的宏观特性，而对于含有纳米尺度孔隙的页岩气储层，无法应用达西定律进行描述，因此，从微观角度研究多孔介质，并建立一套可以描述多孔介质特性的模型，从而为进一步研究多孔介质渗流机理提供一个平台，具有十分重要的工程价值和理论指导意义。

多孔介质模型主要包括毛管模型[1]、球形颗粒堆积模型、格子模型和数字岩心网络模型,主要分为3类：概念模型、统计模型和图像重建模型。随着计算机技术的提高和高分辨率图像扫描电镜的发展，许多学者提出了不同的方法来重建多孔介质模型，重建的数字岩心模型也越来越接近真实地层。本文在Wu Kejian等学者[2-3]研究成果的基础上，结合MATLAB图像处理技术和MCMC方法重建页岩气储层微观结构，为进一步从微观角度研究页岩气储层渗流机理提供基础。

1 多孔介质模型重建方法

数字岩心重建方法主要分为2类：物理实验方法和数值重建方法。物理实验方法主要有CT扫描法、序列成像组合法和 FIB-SEM法。数值重建方法发展较快，主要包括随机法和过程法。

CT扫描技术首先应用于医学领域，Dunsmuir等[4-5]将CT扫描技术应用到石油领域，并通过CT扫描技术和计算机处理技术，得到了岩心的三维图像。但CT扫描仪造价高，试验成本大，不便于大规模应用。

20世纪70年代后,随着计算机技术的发展，随机方法也发展较快，国内外学者提出不同的数值重建方法。迄今为止，发展的随机方法主要包括完全随机法、随机生长法、高斯模拟法、模拟退火法、多点统计法和MCMC法。完全随机方法和随机生长方法比较简单，一般只能用于理论层面的模拟。Joshi[6]于1974年提出高斯模拟法，该方法使用孔隙度和两点相关函数作为约束条件，Quiblier[7]在Joshi的基础上，建立了第一个三维数字岩心，之后很多学者在其基础上进行了改进。Hazlett[6]于1997年提出模拟退火法。

不同于随机建模方法，Bryant、Bakke和Oren等[9-10]提出了通过模拟真实地层的沉积、压实和成岩3个过程来建立数字岩心的方法，并运用此方法建立了Fontainebleau砂岩的数字岩心。与其他建模方法进行对比发现，该模型最大的特点是可以很好地体现真实地层的传导性能。此后，许多学者又进一步进行了研究，Oren和Bakke[11]于2003年综合了随机法和过程法的特点，建立了Berea砂岩的孔隙空间数字岩心模型。

综上所述，通过物理实验方法建立数字岩心，可以比较准确地反映岩心的微观结构，但在实际应用中，由于物理实验方法成本高，过程繁琐，耗时较长，不便于大规模应用。而通过扫描电镜技术，岩心的二维切片图像较易获得，因而通过图像处理技术得到二维切片图像信息并配合数值方法重建数字岩心更适用于理论研究。由于页岩储层结构复杂、孔隙类型多样且孔隙小、含有有机质，建模条件比较复杂，需要考虑的因素较多，综合考虑建立数字岩心的时间、成本以及适用条件，优选出MCMC方法来建立页岩气储层数字岩心。

2 MCMC方法图像重建理论

2.1 二维MCMC方法理论

MCMC法重建图像的主要思路[2-3,12-13]是利用马尔可夫链思想获得转移概率，再利用转移概率进行赋值重建。首先，将二维图形看作一个矩阵，将页岩岩心图像进行二值化，每个点只有0和1两种状态，小于阈值部分代表岩石骨架和大于阈值部分代表岩石孔隙，用公式表示为

(1)

引入领域的思想，认为模型中任何点的状态只取决于相邻少数点的状态。具体地说，就是对于一个特定的点s，用Λ-s表示除s点外的所有点。则存在一个s点的领域Ns，有

(2)

对于2点领域系统，定义影响的某点状态的领域为该点左边1个点；对于5点领域系统，定义影响的某点状态的领域为该点上面的3个点和左边的1个点；对于6点领域系统，定义影响的某点状态的领域为该点上面的3个点和左边的2个点。如图1所示，其表达式分别为

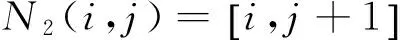
(3)

(4)

(5)

图1 2点、 5点和6点邻域系统示意图

获得条件概率后，就可以利用其为像素赋值，进行图像的重建。重建的步骤为：

(1)利用孔隙度确定(1,1)点的状态，然后利用2点领域模板的条件概率，从左向右依次为(1，j)点赋值。

(2)利用步骤(1)中(1,1)点的状态，利用2点领域模板的条件概率，从上往下依次为(i,1)点赋值。

(3)利用步骤(2)中(1,1)、(1,2)和(2,1)点的状态，采用4点领域模板的条件概率，对(2,2)赋值。同理，从上往下依次为点(i，j)赋值，其中i>2。

(4)采用6点领域模板，从第2行开始从左向右依次为点(2，j)赋值。到第2行结尾时，采用同样方法对第3行(3，j)赋值，依此类推，直至对最后一行赋值，图像重建结束。

(5)对比重构图像与原图的孔隙度，如果达到要求就终止计算，输出最终结果；如果不符合孔隙度要求，则调整条件概率的加权因子，再次开始重构过程，直到符合要求为止。

流程如图2所示。

图2 二维MCMC法重建数字岩心流程

2.2 MCMC方法验证

为了验证MCMC方法是否能反映页岩储层各项异性特点，首先采用四参数生长方法(QSGS)构造几幅各向异性层状介质图像，四参数随机生长方法的控制参数包括孔隙度φ、固相分布概率Pc、方向概率Pi(i=1～8)和概率密度。首先通过调整4个参数中某个参数或某些参数，得到3种不同形貌的多孔介质，如图3所示；其次，对应于随机生长方法和图像处理方法产生的多孔介质，采用MCMC方法分别重建3种不同多孔介质，所得到的重建图像如图4所示，对比重建图像和原图， 可以发现重建图像能很好代表原图的特点。为了进一步验证二维MCMC方法的可靠性， 在此引入2个统计函数单点

图3 应用随机生长方法和图像处理方法产生的多孔介质(白色为孔隙，黑色为基质)

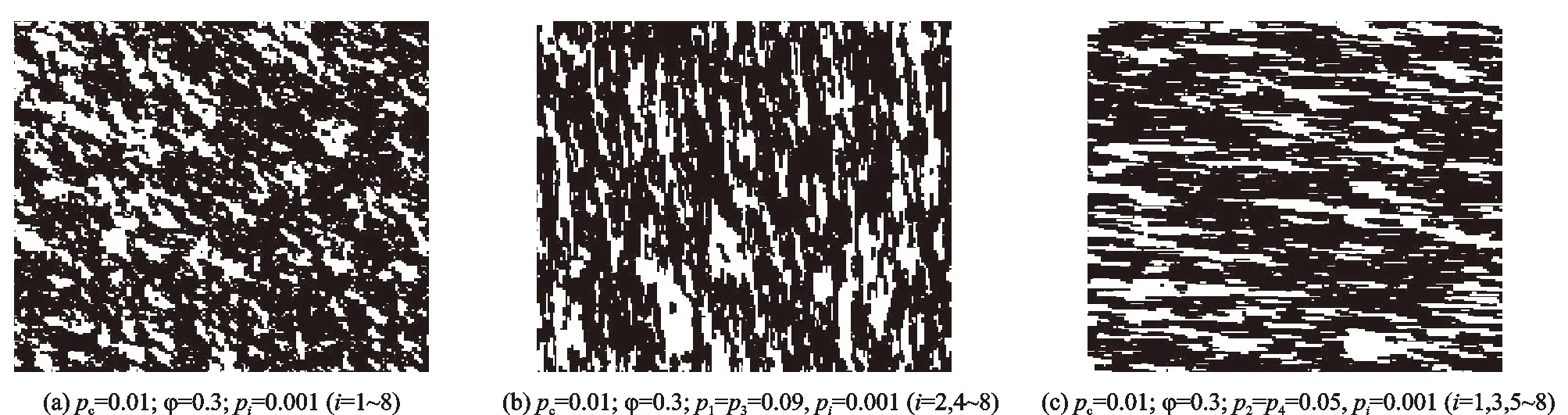
图4 应用MCMC方法重建的多孔介质(白色为孔隙，黑色为基质)

概率函数和自相关函数作为约束条件。

(6)

自相关函数表示相函数在不同位置r和r+h的取值之间的相关程度，对于只考虑孔隙和岩石骨架的两相系统，自相关函数可以当作系统中两点分布于同一相中的概率，自相关函数表达式为

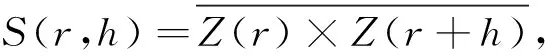
(7)

式中，r和r+h为系统中相距h的任意两点。为了计算方便，令r的单位为像素数，像素与像素边长的乘积即物理长度。

自相关函数是与图像的结构相关的函数，也是评价图像结构性质的重要函数。以图3中前2种多孔介质为例，如图3(a)和图3(b)所示，对比分析2幅多孔介质的重建图和原图的自相关函数，其结果如图5所示，从中可以看出，原图和重建图像的自相关函数吻合性较好，从而说明重建图像可以较好地反映原图性质，即验证了MCMC方法的准确性。

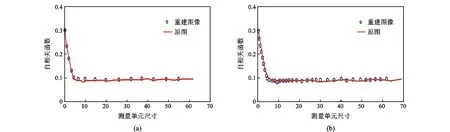
图5 2种多孔介质的重建图与原图自相关函数对比

3 页岩储层数字岩心重建

3.1 孔隙和有机质二值化

根据MCMC方法的需要，首先选取具有代表性的页岩二维切片图像(图6)；根据建模需要，利用二维页岩岩样切片图，用MATLAB软件对孔隙和有机质分别进行二值化，并在二值的过程中对图像进行遍历扫描，基质为0(黑色)，孔隙为1(白色)，有机质为2(红色)，从而可以获得孔隙相对于其他组分的分布特征，以便下一步进行三维数字岩心的重建。提取孔隙和有机质时采用双阈值法[111，134]，有机质和孔隙空间的图像如图7所示，孔隙度为φ0=0.018 1，有机质含量为φc=0.036 24。

图6 某页岩岩样扫描电镜图像 图7 有机质和孔隙空间二值图像

3.2 数字岩心模型的建立

获取孔隙和有机质的二值图像后，应用MCMC方法分别对其进行遍历扫描及二维重建，首先利用MCMC方法对页岩气储层孔隙空间进行重建，重建的孔隙空间模型如图8(a)所示，重建图像中孔隙度(白色)φ0=0.020 5，图中黑色部分代表岩石骨架，白色代表孔隙空间，可以看出，孔隙空间的分布与二维图像特征吻合，多为小而分散的孔隙；重建的有机质模型如图8(b)所示，重建图像中有机质(红色)含量φc=0.036 38；然后将孔隙二维模型和有机质的二维模型进行组合，从而得到完整的页岩气储层数字岩心，如图8(c)所示，该岩心的孔隙度φ0=0.018 5，有机质含量为φc=0.035 79。

3.3 模型的组合

用二值图像对孔隙和有机质进行重建。获得初始模型后将孔隙和有机质组合成一个完整的数字岩心，不同的值采用不同的方法，其具体思路如下：

(1)将不同的初始模型的组分分别赋于不同的值，将孔隙模型中的孔隙和骨架值分别设为0和1，有机质模型中有机质和骨架分别设为2和0；

(2)将不同组分进行相加或者相乘的运算组合起来，获得最终的总模型。

图8 页岩储层数字岩心

组合表达式为

Π=Π1+Π2，

(8)

式中：П为总模型参数；П1为孔隙模型参数；П2为有机质模型参数。孔隙模型中包含基质和孔隙，有机质模型中包含基质和有机质2部分，故其组合类型有4种：

(9)

在组合过程中，由于先放进模型的组分会有部分被后放进去的所覆盖，所以在实际建模过程中，应该结合各组分含量的特点，根据各种组分的重要性，设定优先级。在组合过程中，设定有机质的优先级最高，其次为孔隙度，组合完成后，得到的三维数字岩心如图8所示，该模型的组分特征为：孔隙度(白色)，有机质(红色)，与原始图像吻合性较好。

4 结 论

(1)对比分析数值重建方法，并结合页岩气储层孔隙小、结构复杂、各向异性等特点，优选出MCMC方法来建立数字岩心，结果表明：改进的MCMC方法计算速度快，过程相对简单，并能够反映页岩气储层各向异性特点。

(2)利用四参数随机生长法生成3种不同性质的多孔介质，然后应用MCMC方法进行数值重建，重建的模型能较好体现页岩气储层各向异性和含有有机质的特点，通过分析重建图像和原始图像的自相关函数，发现重建图像能较好反映原图的性质。

(3)利用页岩气储层二维切片图，对孔隙和有机质分别进行二值化，构建各自的数字岩心，组合到一起，得到页岩气储层数字岩心总模型，为页岩气储层微观渗流机理的研究提供了一个模拟平台。

[1]FattI.ThenetworkmodelofporousmediaI,capillarypressurecharacteristics[J].TransAIME,1956,207(a):144-159.

[2]WuKejian,NaoiseNunan,JohnWC,etal.Anefficientmarkovchainmodelforthesimulationofheterogeneoussoilstructure[J].SoilScienceSocietyofAmerican,2004,68:346-351.

[3]WuKejian，MarinusIJ,VanDijke,etal.3Dstochasticofheterogeneousporousmedia-applicationstoreservoirrocks[J].TransportinPorousMedia,2006,65(3):443-467.

[4]DunsmuirJH，FergusonSR,D'AmicoKL,etal.X-raymicro-tomography:anewtoolforthecharacterizationofporousmedia[C].SPE22860，Proceedingsof66thAnnualTechnicalConferenceandExhibitionoftheSocietyofPetroleumEngineers,Dallas,TX,1991.

[5]CoenenJ,TchouparovaE,JingX.MeasurementparametersandresolutionaspectsofmicroX-raytomographyforadvancedcoreanalysis[C].ProceedingsofInternationalSymposiumoftheSocietyofCoreAnalysts,2004.

[6]JoshiM.AClassofStochasticModelsforPorousMedia[D].Kalnsas:UniversityofKansas,1974.

[7]QuiblierJA.Anewthree-dimensionalmodelingtechniqueforstudyingporousmedia[J].JournalofColloidandInterfaceScience,1984,98(1):84-102.

[8]HazlettRD．Statisticalcharacterizationandstochasticmodelingofporenetworksinrelationtoeluidflow[J].MathematicalGeology,1997,29(6):801-822.

[9]BryantS,BluntM.Predictionofrelativepermeabilityinsimpleporousmedia[J].PhysicalReviewA,1992,46(4):2004-2012.

[10]BakkeS,OrenPE.3-Dpore-scalemodelingofsandstonesandflowsimulationsintheporenetworks[J].SPEJournal,1997,2(2):136-149.

[11]OrenPE,BakkeS.ReconstructionofBereasandstoneandporescalemodelingofwettabilityeffects[J].JournalofPetroleumScienceandEngineering,2003,39(2):177-199.

[12] 施尚明,李照永.蒙特卡洛法在吉祥屯气藏储量计算中的应用[J].特种油气藏,2005,12(2):32-34.SHIShang-ming,LIZhao-yong.ApplicationofMonteCarlomethodinJixiangtungasreservoirreservecalculation[J].SpecialOilandGasReservoirs,2005,12(2):32-34.

[13] 王波，宁正福，姬江，等.多孔介质模型的三维重构方法[J].西安石油大学学报：自然科学版,2012,27(4)：54-61.WANGBo,NINGZheng-fu,JIJiang.Studyon3Dreconstructionmethodsofporousmediummodel[J].JournalofXi'anShiyouUniversity:NaturalScienceEdition,2012,27(4):54-61.

[14] 李仁民，刘松玉，方磊,等.采用随机生长四参数生成法构造黏土微观结构[J].浙江大学学报：工学版,2010,44(10):1897-1901.LIRen-min,LIUSong-yu,FANGLei,etal.Micro-structureofclaygeneratedbyquartetstructuregenerationset[J].JournalofZhejiangUniversity:EngineeringScience,2010,44(10):1897-1901.

责任编辑：张新宝

2015-01-16

国家自然科学基金创新研究群体“复杂油气井钻井与完井基础研究”(编号：51221003)；国家自然科学联合基金重点支持项目“页岩气钻探中的井壁稳定及高效钻完井基础研究”之课题“页岩气储层压裂完井优化研究”(编号：U1262201)

张思勤(1988-)，男，硕士研究生，主要从事页岩储层数字岩心建模及渗流机理研究。 E-mail:stemenzhang@126.com

1673-064X(2015)05-0069-06

TE319

A