边界条件对无重管柱螺旋屈曲的影响分析
2015-04-28黄文君高德利魏绍蕾
黄文君,高德利,魏绍蕾
(中国石油大学(北京) 石油工程教育部重点实验室,北京 102249)
边界条件对无重管柱螺旋屈曲的影响分析
黄文君,高德利,魏绍蕾
(中国石油大学(北京) 石油工程教育部重点实验室,北京 102249)
针对无重管柱(忽略管柱重力的影响)螺旋屈曲问题,从虚功原理出发,将管柱边界条件分成2大类。指出前人的研究大多集中于第一类边界条件,而忽略了第二类边界条件。提出塞子模型模拟管柱的端部约束条件,并推导出管柱变形的广义势能泛函。利用最小势能原理,得到了第一类和第二类边界条件下的管柱完全螺旋屈曲段的变形方程,分析了边界条件对螺旋屈曲解的个数和稳定性、管柱与井壁接触力的影响规律。对于端部约束导致的过渡段,通过求解屈曲微分方程得出过渡段长度相对于长管柱整体而言是局部的。最后讨论了长管柱整体变形(完全螺旋屈曲段变形和过渡段变形)与边界条件之间的对应关系。边界条件是导致屈曲问题复杂化的一个重要因素,本文研究结果为深入认识边界条件的影响提供参考。
无重管柱;螺旋屈曲;边界条件;能量法;微分方程;稳定性;接触力
求解管柱屈曲问题的方法主要有2种:能量法和微分方程法,国内外已经有大量利用这2种方法求解管柱屈曲问题的研究。Lubinski[1]利用能量法研究了油管的螺旋屈曲问题,得到了轴向力和螺距之间的关系。Paslay和Bogy[2]利用能量法求解了斜直井眼中管柱的正弦屈曲,得出了正弦屈曲的临界载荷。Chen[3]利用能量法得到了水平井眼中螺旋屈曲的临界载荷。Mitchell[4-8]利用管柱屈曲微分方程对管柱屈曲问题进行了深入探讨。高德利[9-13]、李子丰[14-15]、刘凤梧[16-18]、高国华[19-23]等利用能量法和微分方程研究了管柱的屈曲和后屈曲行为。
从力学原理上,能量法和微分方程法是等效的,因而它们的计算结果也应该是一致的。利用能量法求解时,首先推导出管柱变形的广义势能泛函,再假设屈曲的构型,泛函取最小值时对应的结果即为管柱屈曲解,该方法也称作里兹法。管柱屈曲微分方程是在管柱平衡方程、几何方程和物理方程基础上,考虑管柱和井壁的连续接触条件推导而来的[9]。该方程是一个四阶非线性微分方程,通常利用摄动法、加权余量法、数值方法得到屈曲解。结果也证实这2种方法得到的结果在很多情形下是相同的[9]。然而在以前的分析中,关于无重管柱的螺旋屈曲问题,能量法和微分方程法的求解结果是不一致的。Mitchell[4]利用微分方程分析管柱螺旋屈曲时,得出Lubinski的螺旋屈曲结果只是微分方程结果的一种特殊情况,但没有给出具体的原因。本文深入分析造成该差别的原因,在此基础上将管柱端部的边界条件分成2类,证明了Lubinski的结果只是对应着第一类边界条件,并指出以前能量法求解屈曲问题时通常忽略了第二类边界条件的情形。利用塞子模型来具体刻画管柱端部边界条件,利用改进的能量法,分析了不同边界条件下无重管柱螺旋屈曲解的存在性和稳定性、管柱和井壁的接触力以及管柱端部过渡段的变形规律。最后针对无重长管柱的整体变形,阐明了完全螺旋屈曲段、过渡段的变形与边界条件的对应关系。
1 边界条件
1.1 问题来源
Lubinski[1]利用能量法分析了无重管柱螺旋屈曲问题,得出管柱螺旋线的表达式为
(1)
其中:θ为螺旋线在极坐标系下的角度,rad;F为管柱轴向力,以压力为正,N;EI为管柱的抗弯刚度,N·m2;z为管柱的轴线长度,m。
Mitchell[4]从管柱平衡方程出发,推得了无重管柱的屈曲微分方程
(2)
对方程(2)积分后得
(3)
其中,C0为积分常数,m-3。
假设屈曲解为螺旋线,将θ=ω·z带入到方程(3)中得到
(4)
其中,ω为螺旋线的参数,m-1。
当C0=0时,方程(1)为方程(4)的解;当C0≠0时,方程(1)不满足方程(4),故Lubinski的结果只是微分方程结果的一种特例。
1.2 边界条件的分类
取某一长度的无重管柱作为研究对象,根据虚功原理得到管柱变形满足:
(5)
其中:Ub为管柱变形的弹性势能;F和M代表管柱端部截面(其法线和管柱长度s增大的方向一致)上载荷等效后的集中力和力偶;r和θ代表管柱端部截面的平移位移和旋转角度。将集中力F分解成沿着井筒轴线方向的轴向力和垂直于井筒轴线方向的横向力,则方程(5)右边可以看作是轴向力的虚功与非轴向力(横向力和力偶)的虚功之和。方程(5)可以进一步写成最小势能的形式:
δΠ=δ(Ub+UF+UO)=0。
(6)
其中:Π为管柱变形的广义势能泛函;UF为管柱两端轴向力对应的广义势能;UO为管柱两端非轴向力对应的广义势能。
在Lubinski的分析中,只考虑了管柱变形的弹性势能和管柱两端轴向力对应的虚功,即方程(6)中的前2项,而忽略了δUO的作用。从力学原理上,能量法和微分方程法是等价的,引入了该近似处理,导致Lubinski结果和微分方程结果的不一致。
实际作业中管柱两端的边界条件是很难准确刻画的,例如取某一段管柱进行分析时,该段管柱两端的边界条件受与它相邻管柱段的影响,使得边界条件不能显式表达。此处根据δUO的作用,将管柱端部边界条件分成2类:第一类边界条件满足δUO=0,第二类边界条件满足δUO≠0。
以前的分析中将端部条件通常分为固支约束和铰支约束,约束的作用位置分成在井眼轴线上和井壁上2种情况,如果进一步假设管柱端面只能沿着管柱轴线的方向作平移运动,则管柱端部轴向力的虚功非零,非轴向力的虚功为零,即属于第一类边界条件。前人利用能量法对管柱螺旋屈曲和正弦屈曲进行分析时,对端部边界条件的处理中只考虑了轴向力的虚功作用,忽略了非轴向力的虚功,导致屈曲结果只符合第一类边界条件。Lubinski的分析中也只考虑了第一类边界条件情形。对于第二类边界条件,本文将利用塞子模型来具体刻画,以分析其对管柱螺旋屈曲的影响规律。分析得出当同时考虑第一类、第二类边界条件时,能量法和微分方程法的结果是完全一致的。
2 塞子模型
2.1 模型描述
图1中管柱通过一个塞子来实现其端部的约束,该模型的特点是:
(1)塞子和井筒轴线重合,塞子可以相对于井筒轴线转动;
(2)管柱轴线和井筒轴线平行且间距为rb;
(3)管柱和塞子之间为固支约束,但管柱可以相对于自身轴线自转;
(4)塞子与管柱在轴向上同步运动;
(5)塞子和井筒内壁、塞子和管柱之间的摩阻为零。
(6)在塞子上端中心位置施加轴向力F以及扭矩T。
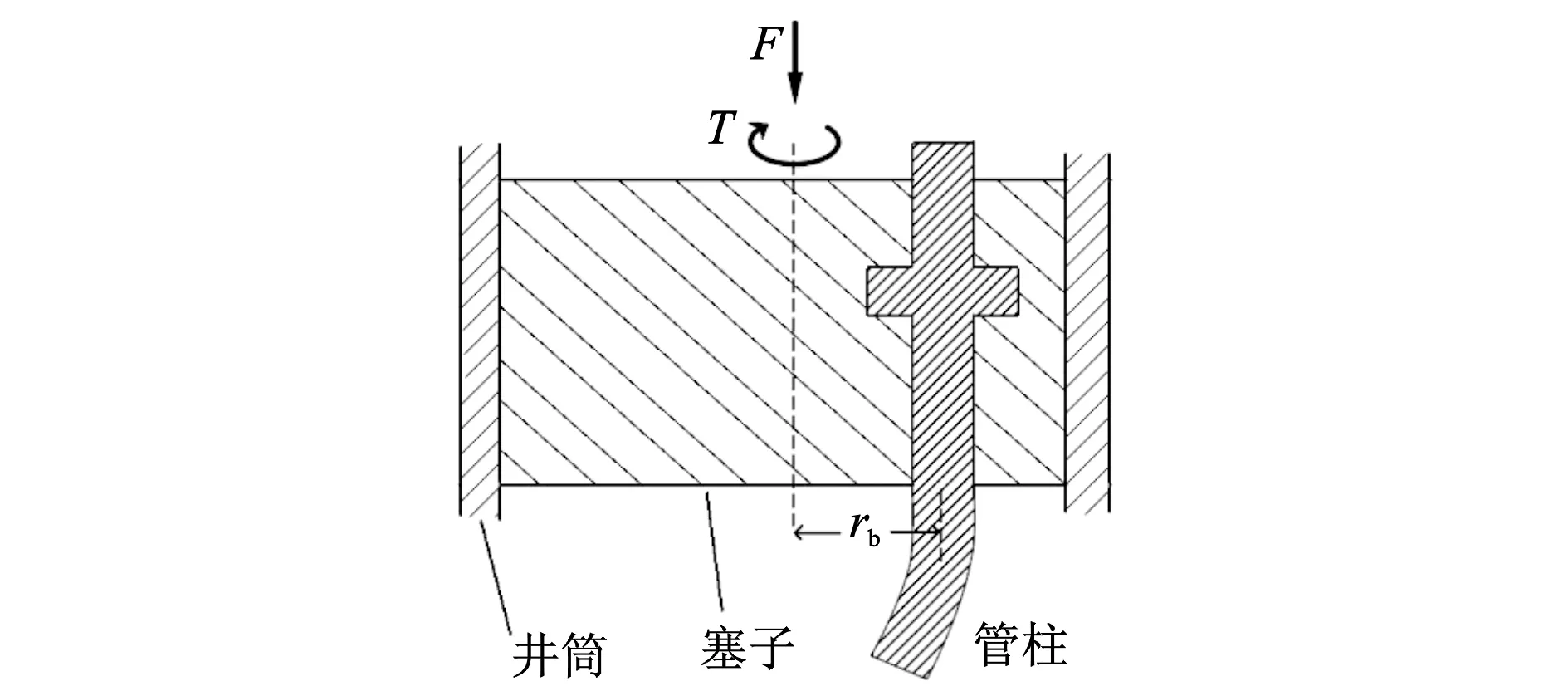
图1 塞子模型
根据塞子上的力平衡,塞子上的载荷F传递到管柱端部上为轴向力F。根据塞子上的力矩平衡,塞子上的扭矩T传递到管柱端部上为横向力,此横向力包含沿着井筒圆周方向的分量FL=T/rb(由于塞子和井筒之间无摩擦,两者接触载荷的方向过塞子轴心,接触载荷相对于塞子轴线的力矩为零,因此,只有管柱对塞子的作用力平衡扭矩T)。管柱可绕自身的轴线自由旋转,因此,管柱上的扭矩MT为零。此处应该注意到塞子上的扭矩T不会影响到管柱上的扭矩MT,在下面的分析中默认MT=0成立。
通常的封隔器模型满足条件rb=0,此时塞子上的扭矩满足T=0。因此,塞子模型可以看作是封隔器模型的一种推广模型。
2.2 改进的能量法
当管柱两端都通过塞子模型来施加约束时,两端塞子上的载荷F和T数值相等,方向相反,如图2所示。此时管柱的变形可分为2种:塞子附近的过渡段a和c;完全螺旋屈曲段b。

图2 受井筒约束的管柱螺旋屈曲
对长管柱而言,塞子附近的过渡段长度相对于管柱整体长度而言可以忽略不计(其证明见4过渡段变形分析),此时塞子中间管柱的变形可利用螺旋线
θ=ω·z
(7)
来描述。假设管柱整体长度为L,则管柱弯曲弹性势能为
(8)
其中rc为管柱的视半径(井筒半径与管柱半径之差),m。
管柱两端轴向力对应的广义势能为
(9)
管柱从直线变成螺旋线,管柱两端的塞子之间产生了相对旋转,旋转的角度为ω·L,其对应的广义势能为
UO=-TωL。
(10)
综合方程(8)—(10),得到管柱变形的广义势能泛函为
(11)
(12)
方程(12)和(4)的形式是一致的,说明能量法和微分方程法对应的结果是一致的。方程(4)中积分常数的计算表达式为
(13)
由此可知微分方程解中积分常数C0与管柱端部塞子上扭矩T直接相关。对于第一类边界条件而言,δUO=0意味着T=0和C0=0,因此,通常的封隔器模型属于第一类边界条件。对于第二类边界条件而言,T≠0,相对于第一类边界条件下的结果将会产生更加复杂的管柱屈曲行为。
3 完全螺旋屈曲段分析
3.1 屈曲解的存在性
β3-β-C1=0,
(14)

根据卡尔丹公式,在复数域内方程(14)存在3个根:
(15)
其中:
(16)


图3 螺旋屈曲解的实根

对于第一类边界条件而言,C1=0,存在3个螺旋屈曲解β=0,±1,分别对应管柱的直线状态和1对相反方向的螺旋屈曲状态。对于第二类边界条件,C1≠0,不仅正反方向螺旋屈曲状态的对称性不成立,而且解的个数也可能变化。同时注意到在第二类边界条件下,塞子上扭矩T≠0,管柱端部的横向力分量FL≠0,导致管柱总是处于弯曲状态,因此不存在直线状态的解(β=0)。
3.2 屈曲解的稳定性
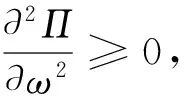
(17)

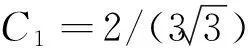
3.3 接触力
不考虑管柱上的扭矩作用时(MT=0),管柱和井壁接触力的计算公式为[9]
(18)
将螺旋线表达式带入到方程(18)中,简化后的结果为
(19)
只有管柱与井壁的接触力为非负值时,管柱屈曲解才是合理的。式(19)中N大于或等于零时,需满足
β2≤2。
(20)

对于第一类边界条件而言,接触力为N=F2rc/(4EI),对应的接触力最大;而在第二类边界条件下,其接触力小于第一类边界条件下的接触力。在实际工程应用中,选择第一类边界条件下的接触力进行设计计算会更加安全。
4 过渡段变形分析
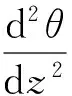
(21)
(22)
(23)
其中无因次积分常数分别为

假设完全螺旋屈曲段的管柱屈曲解为β=β0,带入到方程(21)和(22)中,得到积分常数的计算公式分别为
(24)
(25)
将方程(24)和(25)带入方程(23)中并简化得
(26)
对于第一类边界条件(β0=±1),方程(26)进一步简化为
(27)
方程(27)解的一般形式为
(28)
其中C4为积分常数。从方程(28)可以看出,随着η的增加,β将迅速地接近于±1,即进入完全螺旋屈曲阶段。
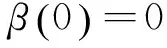
(29)
用数值方法求解方程(26),得到的结果如图4所示。
由图4看出,当无因次长度η达到2π时,可以认为管柱已经进入了完全螺旋屈曲阶段。随着完全螺旋屈曲段β0的增大,过渡段的长度逐渐减小。整体而言,端部约束导致管柱过渡段变形的区间是局部的。
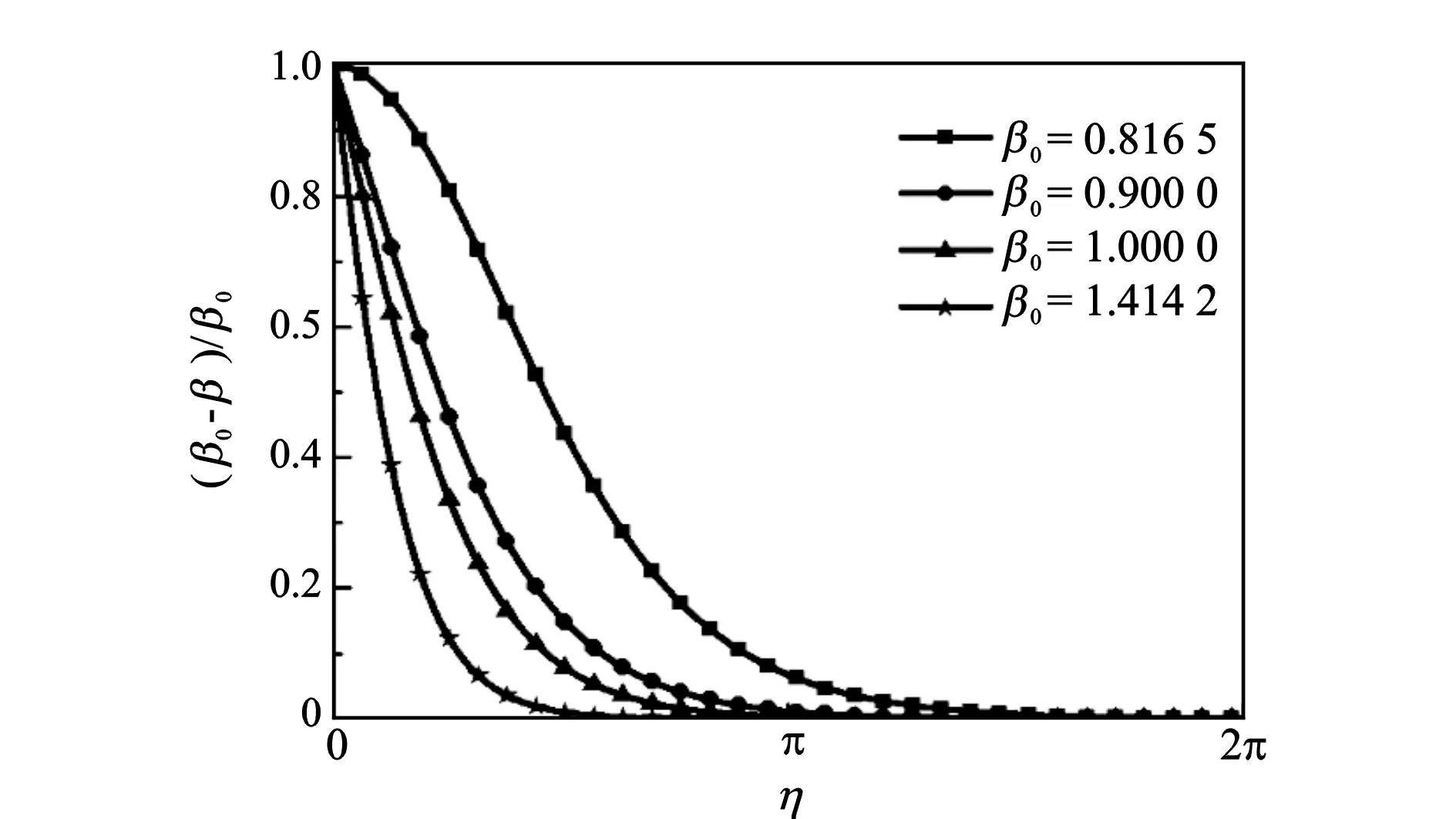
图4 过渡段变形曲线
应当指出,上述过渡段的分析都是在假设长管柱的前提下。与长管柱相对的概念是短管柱,我们认为短管柱是不存在完全螺旋屈曲段,此时过渡段的分析中方程(24)和(25)是不成立的。相对于长管柱,短管柱的屈曲解的形式更加复杂,而且求解也更困难。
5 无重长管柱整体变形与边界条件
由以上的分析可知,无重长管柱的整体变形包括完全螺旋屈曲段和过渡段。完全螺旋屈曲段的变形曲线取决于边界条件C1,然而相同的C1可能对应着不同的边界条件。例如通常研究的铰支和固支约束同时对应着C1=0,对于长管柱而言这2种边界条件下的完全螺旋屈曲段的变形是相同的。

更具体地以塞子模型为例,塞子上的扭矩T和间隔rb都看作是边界条件的参数。当塞子扭矩T发生变化后,完全螺旋屈曲段和过渡段变形曲线发生改变;而只考虑间隔rb发生变化时,完全螺旋屈曲段的变形曲线不变,但过渡段变形曲线发生变化。
不难看出,过渡段和外部约束直接连接,在连接点(对塞子模型而言为塞子和管柱重合的部位,也可以是外力作用在管柱上的位置)处管柱上的位移、应变和应力要和外部约束相匹配,因此一旦外部约束发生变化,则过渡段的变形曲线必然改变。完全螺旋屈曲段和外部约束无直接连接,外部约束以其虚功δUo影响其变形曲线,因而即使外部约束发生改变,只要δUo相同则完全螺旋屈曲段变形曲线也相同。
因此,当忽略过渡段影响时,边界条件的分类方式应该是基于管柱端部非轴向力虚功δUo,而并不是像铰支或者固支这样的分类。本文提出的第一类和第二类边界条件,也只是一种粗略的分类。
6 实例分析
6.1 边界条件对管柱受力影响
本文实例来源于文献[1]中挤水泥过程对管柱受力的影响案例,其主要数据包括:
(1)油管参数:外径Dt=7.0 cm,截面外圆面积Ao=42 cm2,截面内圆面积Ai=30 cm2,截面净面积As=12 cm2,外径与内径之比R=1.178,空气中单位长度管柱重力ws=94.856 N/m,截面惯性矩I=67 cm4;
(2)油管与套管参数:间隙半径r=4.09 cm,套管外径Dc=17.78 cm;
(3)封隔器参数:孔径8.941 cm对应截面积Ap=54 cm2,深度L=3 048 m;
(4)挤水泥作业前参数:地面油管压力pi′=0,地面环空压力po′=0,封隔器油管压力pi=26.2 MPa,封隔器环空压力po=26.2 MPa,油管流体密度ρi=878 kg/m3,环空流体密度ρo=878 kg/m3;
(5)挤水泥作业后参数:地面油管压力pi′=34.47 MPa,地面环空压力po′=6.89 MPa,封隔器油管压力pi=88.18 MPa,封隔器环空压力po=33.10 MPa,油管流体密度ρi=1 797 kg/m3,环空流体密度ρo=878 kg/m3;
(6)挤水泥作业前后温度变化Δt=-11 ℃。
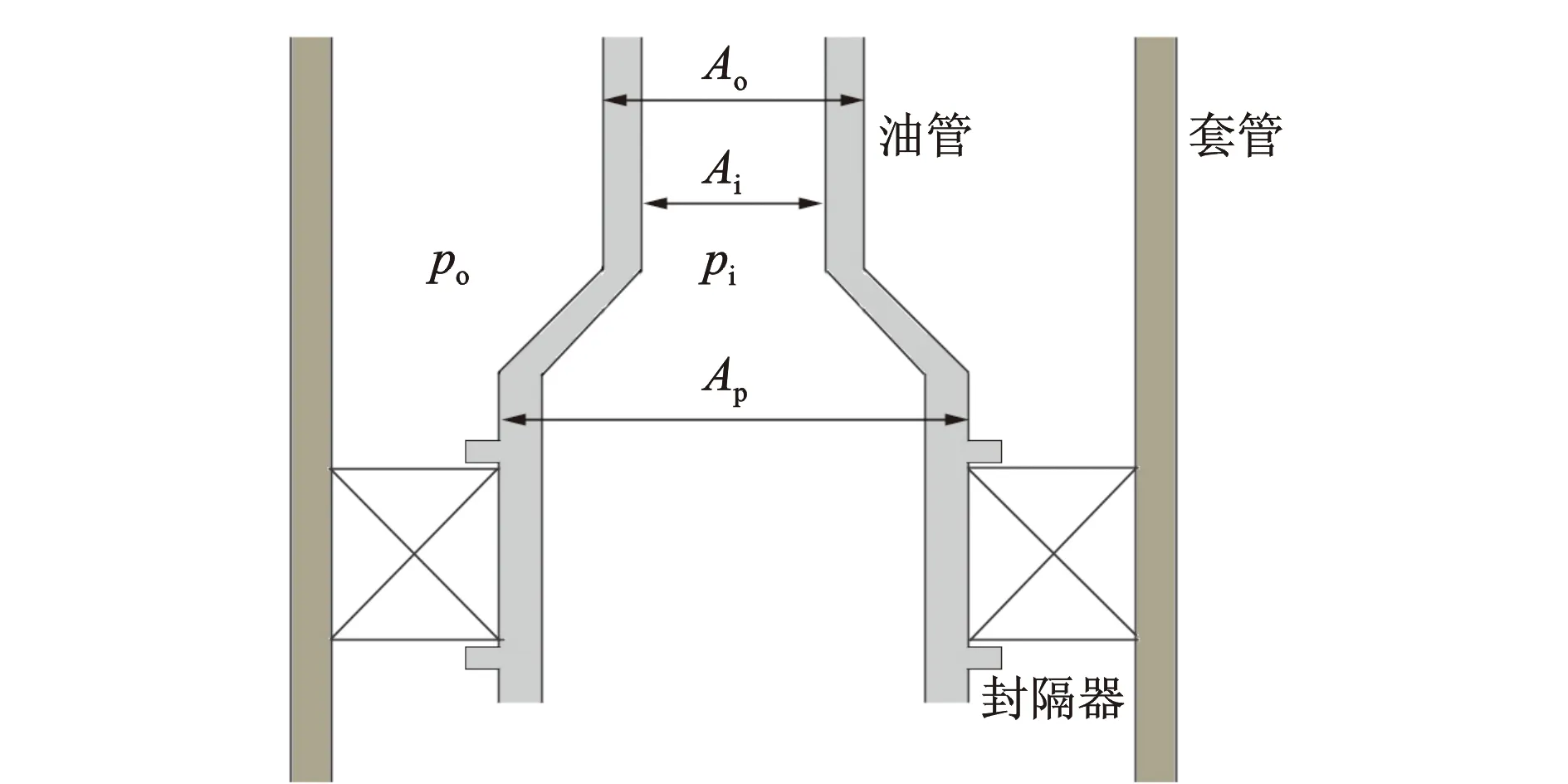
图5 封隔器固定油管位置
为了描述挤水泥前作业参数对挤水泥作业后管柱受力的影响,定义5个力学参数,即挤水泥作业前封隔器对油管的作用力Fs,挤水泥作业后封隔器对油管的作用力Fp,油管在封隔器位置的真实轴向力Fa,油管在封隔器位置的等效轴向力Ff,油管在地面位置的真实轴向力Ft。上述各个参数的具体计算公式见参考文献[1]。结合本文的分析结果,得到上述5个力学参数之间的关系,见图6。
图中case2代表第一类边界条件下的情形,case1和case3代表第二类边界条件下边界条件的参数发生变化的情形。当封隔器与油管的作用力Fs为拉力(pick up)时,第一类和第二类情形的结果基本一致。这是因为管柱基本处于受拉状态,管柱屈曲影响很小。当封隔器与油管的作用力Fs为压力(slack off)时,第一类和第二类情形的结果出现差异,表现为case2近似等于case1和case3的平均情形,case3为管柱最危险的受力状态。这是因为管柱下端处于受压状态,此时管柱屈曲的影响开始变大。尤其当Fs比较大时,如果仍然利用第一类边界条件结果进行计算,则实际受力与计算结果产生很大的误差(例如Fs=300 kN对应的误差达到200 kN)。
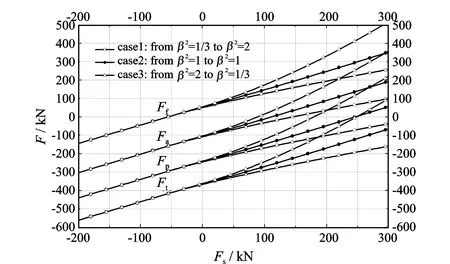
图6 挤水泥作业前后参数变化关系
为了进一步考虑管柱是否发生屈服损坏,定义2个力学参数,即注水泥前封隔器油管内壁和外壁上等效应力的最大值σi,注水泥后封隔器油管内壁和外壁上等效应力的最大值σe。其详细计算公式见参考文献[1],计算结果详见图7。
图中包含了注水泥前后管柱的等效应力计算结果。当Fs为拉力或者压力值比较小时,注水泥后等效应力要高于注水泥前的数值;当Fs为压力且比较大时,在注水泥之前管柱可能更容易产生屈服损坏。当边界条件发生变化后,管柱的等效应力也发生相应变化。在注水泥之前,case3代表最危险情形;注水泥之后,case1代表最危险情形,而case2反映了其平均情形。
利用该图版可以对油管进行优化设计。当-200 kN 图7 等效应力结果 6.2 过渡段长度 根据前面分析可知,当无因次长度η达到2π时,管柱已经进入了完全螺旋屈曲阶段。此处只考虑了第一类边界条件下的情形,给出了3种常用油管对应的过渡段长度与轴向压力之间的关系,见图8。 图8 过渡段长度与等效轴向力的关系 图中可以看出随着油管尺寸的增大,过渡段长度增大。当管柱的等效轴向压力等于零时,过渡段长度趋于无穷;随着等效轴向压力的增大,过渡段长度减小。利用该图版,可以事先对过渡段长度进行估算,从而对管柱力学实验的设计提供参考。 (1)根据管柱端部上的非轴向力的虚功是否为零,将边界条件分成两类。前人利用能量法的研究大多只考虑了第一类边界条件的情形,导致其结果只是微分方程结果的一种特解。当同时考虑第一和第二类边界条件时,能量法得出的结果和微分方程的结果是一致的。 (2)对于完全螺旋屈曲段的变形而言,管柱边界条件存在2个临界值,在临界值两侧螺旋屈曲解的个数和稳定性是不同的,并且管柱边界条件连续变化时,在临界值处螺旋屈曲状态发生突变,螺旋屈曲的方向发生迅速逆转。 (3)对于过渡段的变形而言,其无因次长度一般不超过2π,因而过渡段是局部的。 (4)边界条件对于无重长管柱的完全螺旋屈曲段和过渡段的影响规律是不同的。完全螺旋屈曲段变形取决于端部非轴向力的虚功δUo,导致完全螺旋屈曲段变形和边界条件存在一对多的关系;过渡段变形要满足端部约束的连续性条件,导致过渡段变形和边界条件是一对一的关系。 (5)在第一类边界条件下,管柱螺旋屈曲的管柱与井壁的接触力最大,说明该屈曲解是合理的保守结果。 [1]LubinskiA,AlthouseWS.Helicalbucklingoftubingsealedinpackers[J].JournalofPetroleumTechnology,1962,14(6):655-670. [2]PaslayPR,BogyDB.Thestabilityofacircularrodlaterallyconstrainedtobeincontactwithaninclinedcircularcylinder[J].JournalofAppliedMechanics,1964,31(4):605-610. [3]ChenY,LinY,CheathamJB.Tubingandcasingbucklinginhorizontalwells(includesassociatedpapers21257and21308)[J].JournalofPetroleumTechnology,1990,42(2):140-141. [4]MitchellRF.Newconceptsforhelicalbuckling[J].SPEDrillingEngineering,1988,3(3):303-310. [5]MitchellRF.Helicalbucklingofpipewithconnectorsinverticalwells[J].SPEDrilling&Completion,2000,15(3):162-166. [6]MitchellRF.Lateralbucklingofpipewithconnectorsinhorizontalwells[J].SPEJournal,2003,8(2):124-137. [7]MitchellRF.Effectsofwelldeviationonhelicalbuckling[J].SPEDrilling&Completion,1997,12(1):63-70. [8]RobertFM.Abucklingcriterionforconstant-curvaturewellbores[J].SPEJournal,1999,4(4):349-352. [9] 高德利.油气井管柱力学与工程[M].东营:中国石油大学出版社,2006.GAODe-li.Down-HoleTubularMechanicsandItsApplication[M].Dongying:ChinaUniversityofPetroleumPress,2006. [10] 高德利.井眼轨迹控制[M].东营:中国石油大学出版社,1994.GAODe-li.PredictionandControlofWellboreTrajectory[M].Dongying:ChinaUniversityofPetroleumPress,1994. [11] 高德利,高宝奎.水平井段管柱屈曲与摩阻分析[J].石油大学学报:自然科学版,2000,24(2):1-3.GAODe-li,GAOBao-kui.Effectsoftubularbucklingontorqueanddraginhorizontalwell[J].JournalofChinaUniversityofPetroleum:NaturalScienceEdition,2000,24(2):1-3. [12] 高德利,刘凤梧,徐秉业.弯曲井眼中管柱屈曲行为研究[J].石油钻采工艺,2000,22(4):1-4.GAODe-li,LIUFeng-wu,XUBing-ye.Studyonthebucklingbehaviorofpipestringincrookedhole[J].OilDrilling&ProductionTechnology,2000,22(4):1-4. [13] 高德利,刘凤梧,徐秉业.油气井管柱的屈曲行为研究[J].自然科学进展,2001,11(9):82-86.GAODe-li,LIUFeng-wu,XUBing-ye.Analysisofbucklingbehaviorsofdown-holetubularstrings[J].ProgressinNaturalScience,2001,11(9):82-86. [14] 李子丰,马兴瑞,黄文虎.水平管中受压扭细长圆杆(管)的线性弯曲[J].哈尔滨工业大学学报,1994,36(1):96-100.LIZi-feng,MAXing-rui,HUANGWen-hu.Thebucklingofacircularrodorpipelaterallyconstrainedtobecontactwithahorizontalcircularcylinder[J].JournalofHarbinInstituteofTechnology,1994,36(1):96-100. [15] 李子丰,马兴瑞,黄文虎.油气井杆管柱的静力稳定性[J].工程力学,1997,14(1):17-25.LIZi-feng,MAXing-rui,HUANGWen-hu.Staticstabilityofpipestringinoilandgaswells[J].EngineeringMechanics,1997,14(1):17-25. [16] 刘凤梧.受圆管约束管柱的后屈曲行为研究[D].北京:清华大学,1999.LIUFeng-wu.Post-bucklingbehaviorsoftubularswithincircularcylinders[D].Beijing:TsinghuaUniversity,1999. [17] 刘凤梧,徐秉业,高德利.水平圆管中受压扭作用管桩屈曲后的解析解[J].力学学报,1999,31(2):238-242.LIUFeng-wu,XUBing-ye,GAODe-li.Ananalyticsolutionforpost-bucklingoftubularssubjectedtoaxialandtorsionalloadinginhorizontalcircularcylinders[J].ACTAMechanicaSinica,1999,31(2):238-242. [18] 刘凤梧,徐秉业,高德利.封隔器对油管螺旋屈曲的影响分析[J].清华大学学报:自然科学版,1999,39(8):105-108.LIUFeng-wu,XUBing-ye,GAODe-li.Packereffectanalysisofhelicalbucklingofwelltubing[J].JournalofTsinghuaUniversity:NaturalScienceEdition,1999,39(8):105-108. [19]GaoG,MiskaS.Effectsoffrictiononpost-bucklingbehaviorandaxialloadtransferinahorizontalwell[J].SPEJournal,2010,15(4):1104-1118. [20]GaoG,MiskaSZ.EffectsofboundaryconditionsandfrictiononstaticbucklingofpipeinahorizontalWell[J].SPEJournal,2009,14(4):782-796. [21] 高国华,李琪,李淑芳.管柱在水平井眼中的屈曲分析[J].石油学报,1996,17(3):123-130.GAOGuo-hua,LIQi,LIShu-fang.Abucklinganalysisofpipestringinhorizontalboreholes[J].ActaPetroleiSinica,1996,17(3):123-130. [22] 高国华,李琪,李淑芳.弯曲井眼中受压管柱的屈曲分析[J].应用力学学报,1996,13(1):115-120.GAOGuo-hua,LIQi,LIShu-fang.Bucklinganalysisforpipestringconstrainedincurvedboreholes[J].ChineseJournalofAppliedMechanics,1996,13(1):115-120. [23] 高国华,张福祥,王宇,等.水平井眼中管柱的屈曲和分叉[J].石油学报,2001,22(1):95-99.GAOGuo-hua,ZHANGFu-xiang,WANGYu,etal.Bucklingandbifurcationofpipesinhorizontalwells[J].ActaPetroleiSinica,2001,22(1):95-99. 责任编辑:田美娥 2014-08-30 国家科技重大专项课题“复杂结构井优化设计与控制关键技术”(2011ZX05009-005);国家自然科学基金创新研究群体(51221003) 黄文君(1986-),男,博士,主要从事油气井管柱力学研究。E-mail:huangwenjun1986@126.com 1673-064X(2015)03-0087-08 TE24 A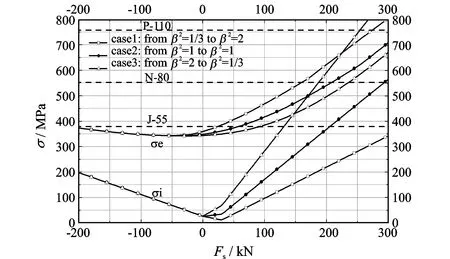

7 结 论
