中美国债市场溢出效应研究——基于集合经验模态分解

闫树熙，刘 伟

（1.榆林学院 数学与统计学院，陕西 榆林 719000；2.西安交通大学 经济与金融学院，陕西 西安 710061）

【统计应用研究】

中美国债市场溢出效应研究
——基于集合经验模态分解

闫树熙1，刘 伟2

（1.榆林学院 数学与统计学院，陕西 榆林 719000；2.西安交通大学 经济与金融学院，陕西 西安 710061）

集合经验模态分解（EEMD）是目前国际公认的可以有效处理非平稳非线性时间序列的方法。在中美融合不断加深的背景下，首次将该方法用于中美国债指数的分解，筛选出的低频分量及趋势项能够有效表征原始序列。基于此建立了二元VAR-GARCH-BEKK模型，从均值与波动两个维度考证了中美国债市场的溢出效应，结果发现：面对重大事件及经济政策的冲击，两国国债之间表现出双向的均值溢出，但影响程度不对等，美国对中国的溢出相对较强，而波动溢出效应则是对称的；国债市场长期运行过程中，两国具有双向的波动溢出，但仅存在美国对中国的单向均值溢出。中国应进一步完善国债市场交易机制，丰富国债交易品种，加强金融市场监管等，来有效对冲美国市场对中国的溢出效应，防范与化解系统性风险。

集合经验；模态分解；国债市场；溢出效应

一、引 言

金融市场上的溢出效应，是指由于贸易投资的基本面因素、“羊群效应”的行为范式及信息传递的启发式准则等引起的不同金融产品价格或市场之间的同步涨跌或波动现象。伴随着世界经济一体化与金融全球化步伐的持续加快，金融溢出效应越来越呈现出跨市场和跨品种的传播与蔓延。就一国资本市场来说，来自外部的溢出性是一把“双刃剑”，具有典型的双重属性。一方面，适度的外部资本流入可以保证市场充足的流动性，同时能带来先进的投资理念甚至倒逼金融制度的不断完善；但另一方面，过度、扭曲的溢出效应往往冲击金融市场的平稳健康发展，甚至造成系统性风险，进而致使危机的出现。近年来，作为世界经济总量前两位的美国及中国不断深化经贸合作，新一届中国政府提出全方位建设中美新型大国关系，可以预料中美未来各方面尤其是资本市场的互融互通会进一步加深，这势必对中国金融市场的建设与运行产生重要影响。在这样的背景下，研究中美资本市场之间的溢出效应，其意义不言而喻。

股票市场市值规模大、机制相对成熟，一定程度可以代表资本市场的发展水平，因而长期以来，国内外学者针对不同阶段中美股市间的溢出效应进行了系统性研究。陈守东等应用协整分析和误差修正模型实证分析了1992-2002年沪、深及美国等主要国家和地区股市之间的关系，结果发现中国股市与美国等市场相分离[1]；韩非和肖辉采用MA（q）-GARCH（1,1）-M框架、陈潇和杨恩建立T（E）GARCH-G模型，分别研究了2000-2004年及2001-2010年的中美股市，所得结论均与陈守东等的结论相一致[2-3]。但是也有文献得出截然相反的结果。游家兴和郑挺国基于非对称M-GARCH模型，检验了1991-2008年中国同美国等主要国际经济体股市之间的协同作用，发现在中国金融自由化政策逐渐推进和稳步深化的形势下，中国同美国等市场的联动性越来越强[4]；西村友作通过EGARCH模型和CCF检验法，考证了2000-2007年的中美股市的相依性，结果证实两市间联动性的存在[5]；同样结论的研究还有张兵、Luo等[6-7]。随着中国金融体系的逐渐完善，学者们也对中美其他金融市场间的溢出性进行了探索。冯涛和刘伟在次贷危机及欧债危机的叠加影响背景下，从收益率的视角探究了中国同欧盟及美国债券市场的关联性，结果表明中国同欧美债券间不具有均值溢出，但存在双向的波动溢出[8]。李成等采用多元非对称VAR-MVGARCH（1，1，1）-ABEKK模型，实证分析了次贷危机前后中美两国利率的联动机制，发现二者之间存在显著的波动溢出，美国利率上升或下降对中国利率波动以及中美利率协动性的影响具有非对称效应，且危机以后中美利率联动程度进一步加大[9]；刘威和吴宏的研究也证实了该结论[10]。

针对已有文献，我们可以从三个方面来进行梳理。第一，研究对象方面，关于中美资本市场的溢出效应，学者们关注的焦点在于股票市场，先后从不同视角，采取多种实证方法就各个时期的联动性进行了考证，且得出了较多富含建设性的结论，尽管这些结论并不一致。相比之下，涉及两国间其他金融市场及产品，尤其对债券市场的研究较少。缺乏债券市场的相关研究，会使已有结果不够全面，无法真正反映资本市场间的协同作用；第二，数据处理方面，已有文献选取与加工指标时，往往直接以原始收盘价或经收盘价计算的收益率为研究对象，这是一种总量的数据采集。金融高频时间序列的总量效应表现为多种分量作用的综合结果，可以从时域和频域两个维度进行结构分解。在不同阶段，由于经济环境及政策的影响，序列总量的各分量未必有相同的外在表现，有时可能相悖，因而若不加以结构分解，简单以总量数据来进行实证研究，极有可能无法界定金融变量真实的传导路径，从而降低了结果的准确性。第三，实证计量方面，绝大多数文献都是从均值或波动的单一维度来检验市场间的溢出关系，很少从这两个方面同时进行研究。均值是指一阶矩，是对统计对象的本质规律的反映，而波动是指二阶矩，用以测度信息等外部因素变化导致对均值的偏离程度，因而单维检验不能全面对产品及市场间的动态传递效应进行综合度量，可能致使结果有所偏颇。

基于上述考虑，为扩展已有研究，本文拟从国债市场出发，首次将集合经验模态分解方法用于中美国债市场指数，筛选出恰当的结构分量后，构建二元VAR-GARCH-BEKK模型，同时从均值与波动两个层面来检验中美债券市场的溢出效应，以期探明中国国债是否或如何受到美国债券的影响，从而为管理层完善金融市场，以及防范系统性风险提供实证借鉴。

二、集合经验模态分解概述

金融时间序列具有非平稳的内在特征，为了达到计量模型的要求，经常不得不采取对数差分等形式变换，虽然一定程度上消除了非平稳性，但也遗漏或改变了原始数据本身所蕴含的相关信息，只能是一种次优的处理方式。一种新的工程领域信号分析方法——经验模态分解（Empirical Mode Decomposition，简称EMD），在处理非平稳时间序列时却具有很大的优越性，被国际公认为对以线性平稳为前提条件的傅里叶分析及小波变换等传统时频分析规则的重大突破[11]。它无需对原始序列先验处理，可直接自适应且完备地分解数据，真正做到了让数据自己说话。EMD最早由Huang等于1998年设计出并开始用于工程领域数据分析，且在2003年将其引入金融计算，基于其强大的自适应提取不同频谱分量的功能，来深入挖掘非线性非平稳时间序列的内在波动规律[12-13]。

EMD处理数据的原理可以表述为：它经过一系列的迭代筛选过程，从原始数据中分解出若干不同频率的固有模态函数（Intrinsic Mode Function，简称IMF）和一个趋势项，其中不同的IMF揭示了序列本质的不同波动特征，趋势项反映了序列固有的内在长期运行轨迹。分解得到的IMFs须同时符合两个要求：一是总体序列的极值点及零值点数量相等或不超过一个，二是由局部极值点确定的上下包络线的均值为零。

EMD的算法简析如下：第一步，用三次样条法将原始时间序列x（t）的局部极值点依次连起来形成序列上下包络线，然后求出其平均包络线序列m1（t），有m1（t）=（Max（t）+Min（t））/2；第二步，从原序列x（t）中去除掉平均包络线m1（t）得到一个不包含低频数据的新序列，有h1（t）=x（t）-m1（t）；第三步，若新序列h1（t）符合IMF的两个要求，则将其视为分解得到的第一个IMF，有c1（t）=h1（t），否则，对h1（t）重复前两步的操作直至满足要求；第四步，将生成的新序列r1（t）作为新的原始序列重复以上操作，顺次得到第2、第3直到第n个IMF，记为cn（t），这里有r1（t）=x（t）-c1（t）。IMF的个数，可由连续两个分解结果之间的标准差的大小来判定，当cn（t）小于一个预设值或剩余部分是一个单调的序列时，整个筛选过程结束。对于该点，实际计量过程中，可通过判断按顺序分解得到的IMF的均值是否显著不为零来实现。由于整个分解过程IMF的滤出顺序是由短周期到长周期即从高频到低频，因而当第i个IMF的均值显著不为零，则可以判断出之前的所有IMF均为高频函数，相应的包括第i个及后面的IMF均为低频函数。于是，最终通过这样的频带分解过程将原始时间序列分解为高频、低频与趋势项三个子序列。根据不同分量的自身特征及对原始序列的贡献度，就可以揭示出原始序列的真实规律以及能够准确客观表征原始序列的结构分量，从而可以选择恰当的子序列进行针对性的有效研究。

但是通过经验模态分解，容易造成同一个IMF是由若干个不同周期的时间序列汇聚的结果，相应的也会有相近周期的序列反而分散在不同的IMF中，致使结构分解的物理意义不够清晰，即“模态混叠”[11]。另外“端点效应”问题也较为突出（具体内容省略，详见Wu和Huang的研究成果[14]）。针对这些缺陷，Wu和Huang通过给原始序列加入白噪声，在EMD方法的基础上发展出了集合经验模态分解（Ensemble Empirical Mode Decomposition，简称EEMD），做出了较好的改进。EEMD方法的原理是基于白噪声的频率均匀分布的统计学特点，将其加入原始序列后，使得原序列的极值点有所变化，进一步保证了不同频率的连续，促进抗混分解，减少模态混杂。EEMD的算法同上述关于EMD的算法高度类似，既有文献已有相关概括。

三、基于EEMD的中美国债市场走势分析

从短、中、长期的期限结构角度，政府债券一般包括3月、6月、1年、2年、3年、5年、10年甚至30年和50年等诸多种类，相应有各自的交易收盘指数，然据此进行实证检验往往只能针对特定期限的国债市场，无法从总体上进行考量。有鉴于此，本文选取金融时报政府债券指数，该指数由英国《金融时报》结合各国政府债券的种类、规模及期限等因素进行加权计算编制得出，测度了各国政府债券每个交易日的变化，在全球范围内具有重要影响。研究时限从次贷危机至当前，即2008年1月2日至2015年1月2日，扣除掉节假日及不重叠的交易日，样本包括中美2组共计3 560个数据。

表1 中美国债指数的描述性统计

注：***表示统计量在1%的水平下显著。

表1列示了中美两国国债指数的统计特征。可以发现，美国国债指数无论是均值、中值还是最大值或最小值均高于中国国债指数，且其波动性也较高；两国国债指数偏度系数为正，二者分布有长的右拖尾，即右偏；中国国债指数的峰度大于3，美国国债指数小于3，说明二者分布的凸起程度分别大于和小于标准正态分布；JB统计量较大也表明在1%的显著性水平下，拒绝两国国债指数序列正态分布的原假设。这些充分说明中美国债指数的分布具有高频金融数据典型的非正态特性；两个指数序列的ADF统计量绝对值小于10%显著性水平下的临界值，说明两序列为非平稳序列，可以使用EEMD方法进行结构分解。

为了更直观地展现中美两国国债市场的运行情况，图1描述了考察期内二者的变化态势，可以发现，双方保持着较为同步的长期走势，从2008年次贷危机爆发至2013年4月，这一期间中美国债市场较为平稳，而从2013年4月至今，两国走出了高度一致的巨幅震荡行情。下面通过EEMD来进一步剖析二者的内在结构特征。

图1 中美国债市场走势

图2描述了基于EEMD的中美国债市场的结构分量走势图，从中可以看出，经过频带分解，中美国债均包含9个模态函数和1个趋势项。二者依次分解出的IMFs的振幅随着周期从短期向长期（即波动频率从高频向低频）的增大而逐渐扩展，尤其最后1个分解单元——趋势项r完全呈缓慢的单调递增的变化，体现了中美两国国债市场的长期发展趋势。

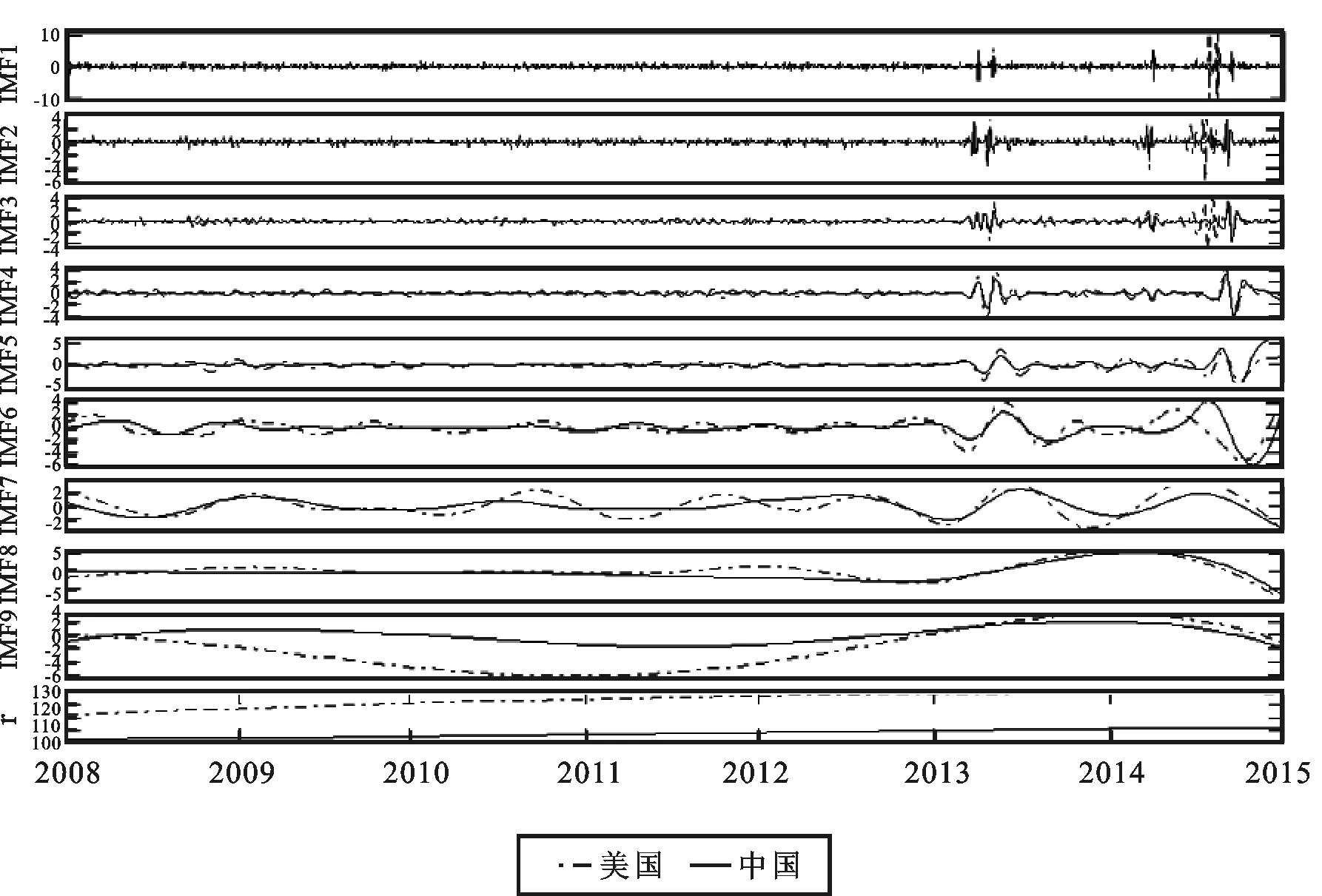
图2 基于EEMD的中美国债结构分量走势

为了更好地揭示中美国债市场的时频变化，从以下三个方面来对经过EEMD得到的分解结果做出具体分析：1.均值。各IMF的均值测度了相应分量的长期变化及对整体的平均贡献度。2.相关系数。用各IMF和原始序列的相关系数来测度各分量同整体的相关程度；同时，为了保证结果的稳健性，我们进一步对中美两国国债分解得出的对应IMF进行相关性检验。3.方差占比。各IMF的方差与分解后的总方差的比例反映各分量对原始序列波动幅度的贡献度。需要说明的是，各IMF的方差之和同初始序列的方差并不相等，原因在于初始序列的非线性及在分解过程中对其施加了三次样条法的结束条件[15]。具体分解结果如表2。

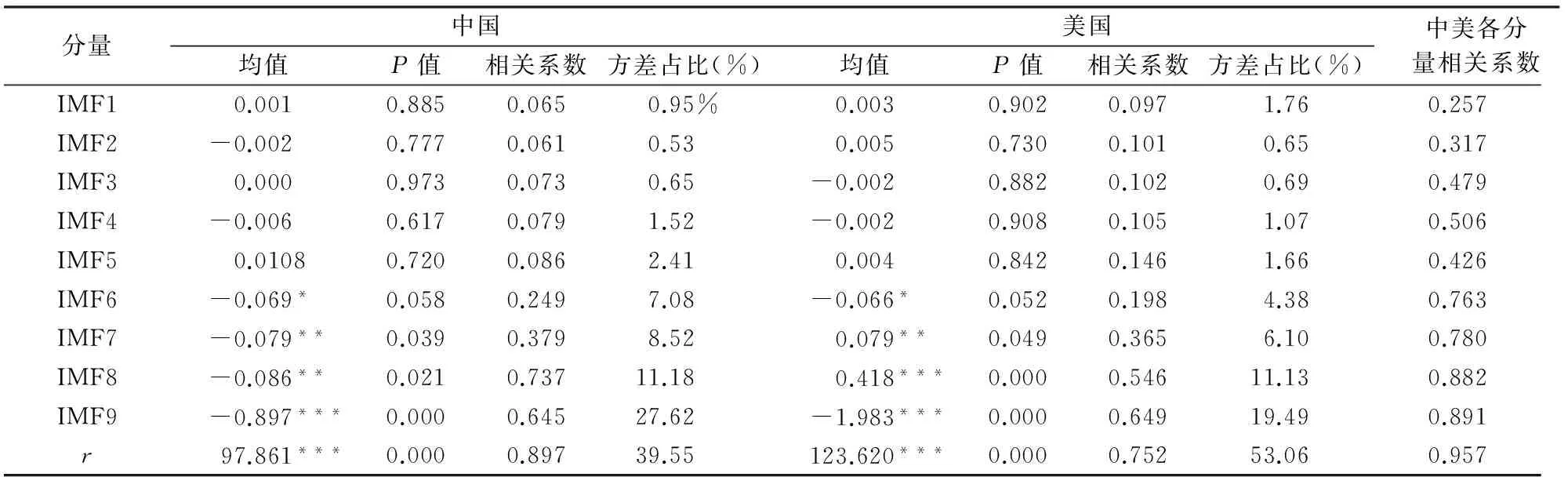
表2 基于EEMD的中美国债固有模态函数IMFs及趋势项r分析

注：1.*、**及***分别表示在10%、5%及1%的水平下显著，下同；2.各数据基本取了小数点后三位，与真实数据有极微小出入。

观察表2，对中美国债分解得到的两组分量的均值都是从第6个分量起显著不为零，从而根据EEMD的算法原理可判断出前5个IMF属于高频分量，后4个IMF为低频分量，趋势项r为独立分量。从经济学意义讲，高频分量因振幅偏小，周期较短，主要反映了金融时间序列所蕴含的一般信息，体现了债券指数的随机非均衡波动，传递给投资者有关债券市场短期的表面信号；低频分量因周期相对较长以及波幅较大，往往能对初始序列进行较为直观的刻画，主要表征了债券市场对于重大经济政策及突发事件冲击的响应；而趋势项因其运行轨迹变化缓慢，且在长期中呈现单调递增态势，体现了金融时间序列中较为稳定的信息，反映了初始序列的内在本身特征变化规律（如图3所示，考察期两国国债走势均围绕趋势项上下波动），长期看可作为债券市场的核心构成部分，对投资者判断债券市场现时及未来行情意义重大。就不同的结构分量，已有文献指出高频分量一般不是分析的重点，研究往往聚焦于低频分量和趋势项[16]。本文是否遵循该判断，我们需进一步讨论。表2中两组分量由高频向低频被依次筛选出，相应的其与原始序列的相关系数逐渐递增，其中趋势项与原始序列的相关性最高，分别为0.897和0.752，低频分量稍次之，但也远高于高频分量；高频分量的方差占比极小，合计均在6%左右，低频分量的方差占比明显上升，合计分别达到54%和41%，趋势项的方差占比最高，分别为40%和53%。

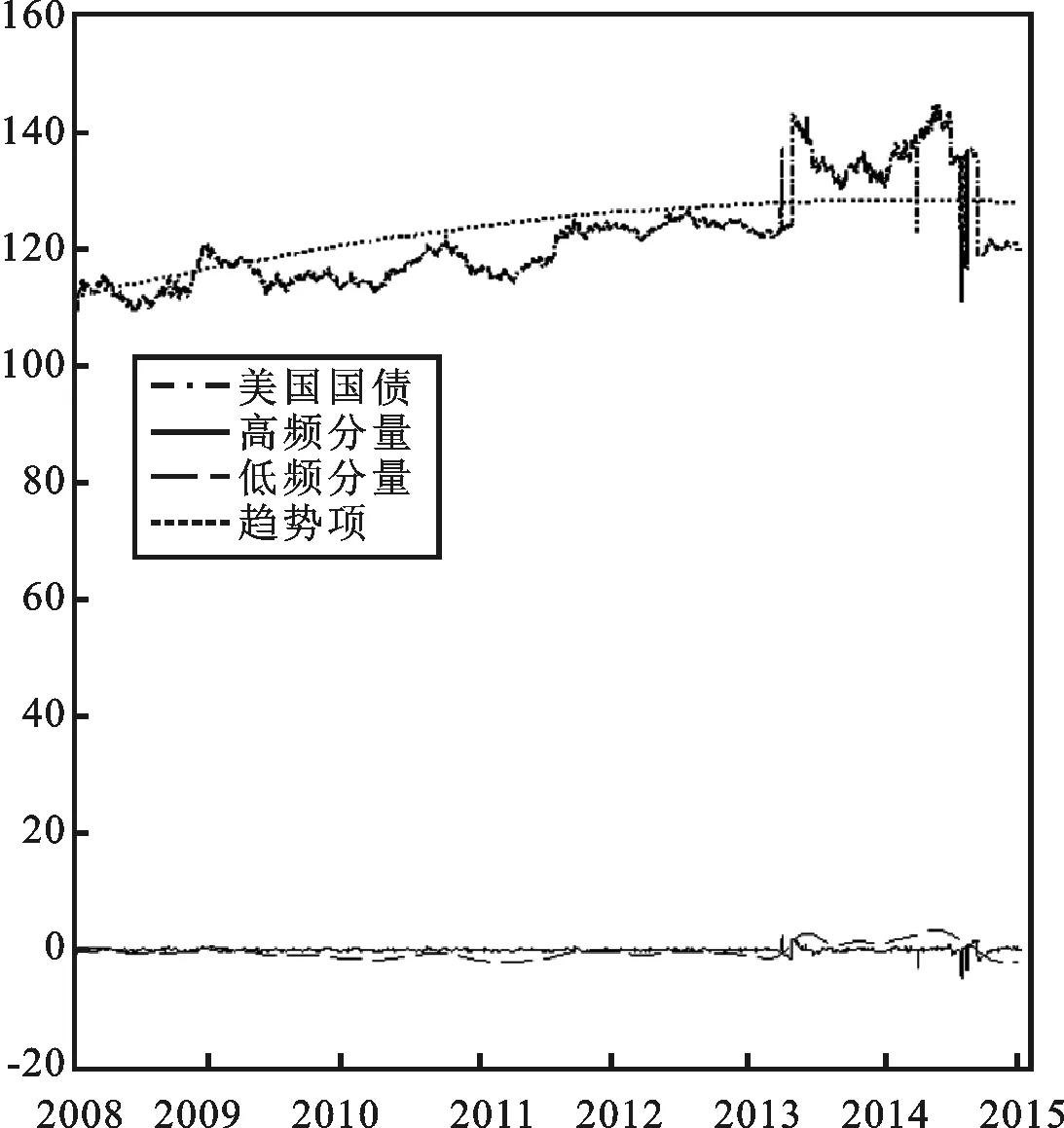
图3 中美国债总量及结构分量走势

因此，经过上述定性与定量分析，可以认为低频分量与趋势项能够较好地代表国债市场的基本走势，即能够较为准确地反映国债市场行情。与此相对应，表2中最后一列给出了中美国债两组结构分量之间的相关系数，同样可以看出，高频分量之间相关性较低（基本低于0.5），而低频分量之间相关性较高（0.76～0.89），趋势项之间相关性最高（0.957），说明两国国债市场可能存在的溢出效应基本由各自的低频分量和趋势项之间的关系所呈现。这也在某种程度上给出了上述判断的稳健性支持。此外，从微观投资的角度看，国债市场不同于股票市场，后者因频繁遭受内外部诸如公司经营状况及多空力量等因素影响而致使股价易于波动，但往往是短期波动，而对于国债的投资更多是对主权国家信誉、政府经济制度及货币币值等的关注与考量，由于这些因素一般通过中长期来反映，自然同样会将研究的焦点集中到低频分量与趋势项上来。因此，下面就从低频分量及趋势项出发，来考证中美两国国债市场之间的溢出效应。

四、从均值和波动的双重检验看中美国债市场溢出效应

（一）模型构建

本文在向量自回归（VAR）模型的基础上，通过对回归方程的残差项进行进一步的波动检验（GARCH），旨在从均值及波动两个层面来考证中美国债市场的关联性，因而构建了一个二元VAR-GARCH-BEKK模型。

1．均值溢出。对于多个经济变量的计量研究，传统的联立方程结构性方法以经济理论为基础来描述，但通常无法具体反映多个变量之间的动态关系，尤其是允许内生变量可以同时出现在方程的左右两端，导致系数估计与方程预测极为复杂，而向量自回归（VAR）模型很好地解决了这一问题。

以CB和UB分别代表中美国债，限于篇幅，这里不对VAR模型的基本形式作出描述，直接给出本文所用的具体模型：

（1）

式（1）中，系数α、β分别表示中美国债对自身及对方市场的均值溢出影响，可通过参数t检验来判断其显著性。

2.波动溢出。传统计量经济学一般假定时间序列模型的随机扰动项的方差（即序列的波动）较为稳定，仅仅存在序列相关问题，但后来研究发现扰动项方差与时间变化有关并依赖于过去时期误差的大小，具有条件异方差性。自回归条件异方差（ARCH）模型与广义自回归条件异方差（GARCH）模型考虑到了扰动项方差不一致带给模型的影响，且后者保证了条件方差的非负性。基于一元GRACH模型基础上的多元GARCH模型可以度量多个变量之间的波动性关系，关注不同市场之间的风险传递情况，众多的GARCH族模型中，BEKK模型可以保证由均值方程残差项构成的条件方差方程的方差-协方差矩阵正定，而且方差方程待估参数个数较少，因此，本文选择BEKK（1,1）模型来作为波动溢出效应的检验方法。

首先，构建如下模型：

（2）

将上述元素带入模型（2），展开即得到h11,t（中国）和h22,t（美国）国债市场的条件方差方程*展开共有4个方程，本文的焦点在于判断中美两国国债之间的相互波动影响，因而只需关注h11,t和h22,t。，这里仅分析h11,t的影响因素及假设检验，h22,t同样适用。

（二）实证分析

1.平稳性检验。由于VAR模型建立在变量平稳的基础上，因此我们先对中美国债相关序列进行单位根（ADF）检验，结果如表3所示。从表中可以看出，尽管中美两国国债的原始时间序列非平稳，但两组低频分量及趋势项皆为平稳序列 ，从而可以展开实证。

表3 中美国债总量及各分量的ADF单位根检验

注：ADF的检验形式（是否包含截距项或趋势项）及滞后期的选择由实证软件系统默认。

2.均值溢出检验。经过反复实验，发现分别对低频分量CBDt与UBDt及趋势项CBQt与UBQt建立滞后2期的VAR模型时*由于低频分量各有4个，本文进行检验时为了不失一般性，分别以两组低频分量的平均值作为实证标的，且为了确保结果具有稳健性，我们同时做了各低频分量间的VAR模型，估计结果发现系数方向均保持一致，数值略有微小出入，不影响结论的准确性。，赤池信息和施瓦茨信息的数值均最小，同时，特征根检验显示两组根的倒数皆位于单位圆之内，说明模型具有稳定性（滞后期选择及特征根检验详细过程未列示），因此，VAR（2）模型为最优选择，结果见表4。

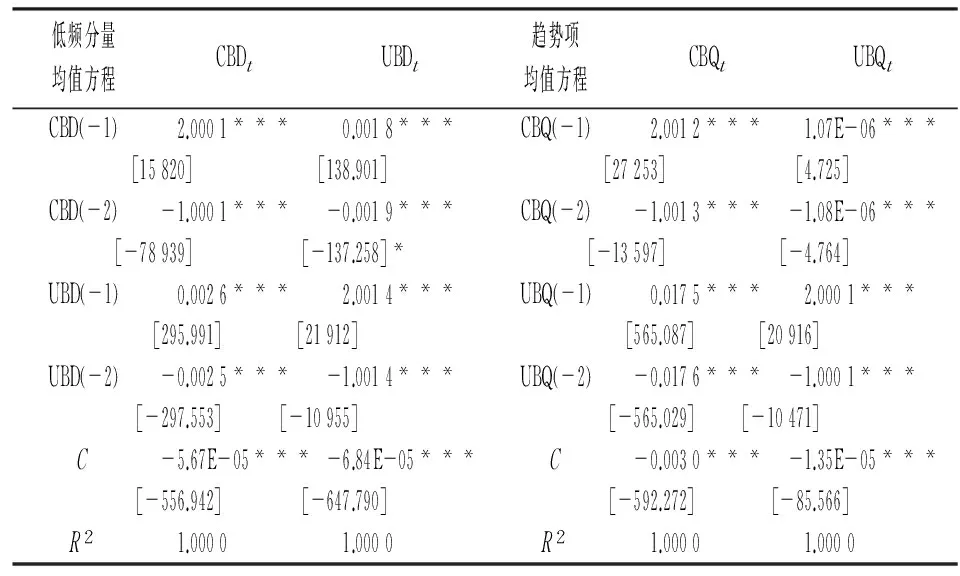
表4 低频分量CBDt与UBDt及趋势项CBQt与UBQt的VAR（2）模型估计结果

表4表明，中美两国国债低频分量的VAR模型及趋势项的VAR模型估计系数均高度显著，且可决系数R2近乎为1，说明两个均值溢出检验模型的拟合度非常优秀。从低频分量来看，面对重大经济决策及异常事件的冲击时，两国国债行情均体现出一定的自身惯性，而后迅速反转，其中中国国债前一交易日变动1个单位引起自身当日同向变化2个单位，但前两个交易日变动1个单位引起自身当日反向变化1个单位。美国国债市场遵循同样的规则，说明两国国债均呈现出典型的波浪式运行轨迹。关键在相互影响方面，美国市场前一交易日1个单位变动引起中国市场0.002 6个单位的同向变化，前两个交易日1个单位变动引起中国市场反向变化0.002 5个单位，相应的，中国市场的变化同样可以传导至美国，只是程度上相比较低（前两日的影响分别为0.001 8和-0.001 9）；趋势项上，两国国债在长期潜在发展过程中，同样体现出波浪式的惯性走势，且美国市场前一交易日1个单位变动引起中国市场0.017 5个单位的同向变化，前两个交易日1个单位变动引起中国市场反向变化0.017 6个单位，所不同的是，尽管通过了系数显著性检验，但是中国对美国的影响微乎其微。

总体上来看，从均值的角度分析，在突发事件冲击及各种政策效应下，中美两国国债间具有双向协同性，相对来说美国对中国的溢出效应稍大，而在市场长期的内在运行过程中，仅具备美国对中国的单向溢出。

3.波动溢出检验。通过ARCH-LM检验法及残差平方相关图检验法，均拒绝了上述两组均值方程的残差项不具有ARCH效应的原假设，从而说明可以针对两组残差项建立GARCH-BEKK模型，来研究中美国债市场之间的波动溢出效应。经过检验，发现标准化后的残差vt不具有ARCH效应，说明本文波动溢出效应模型建立准确。具体估计结果如表5。

表5 低频分量及趋势项的GARCH-BEKK（1,1）模型估计结果

表5表明，低频分量波动溢出模型及趋势项波动溢出模型的估计系数均通过了显著性检验，且两国国债的波动保持一定的惯性，受自身影响程度较大，再次验证了金融时间序列的聚集性特点，这也同上面从均值角度得出的具有自相关性的结论保持一致。同时，表6列出了两组波动方程的检验结果，可以看出，无论是“一国到另一国不存在单向波动溢出”，抑或是“两国之间不具有双向波动溢出”的原假设均被拒绝，都证明了中美两国国债在波动层面具有相互溢出效应。

表6 中美国债波动溢出效应检验结果

至此，我们在对中美两国国债指数进行总体经验模态分解的基础上，从均值与波动两个视角探讨了二者的溢出性，其中关于低频分量的研究结果表明中美两国具有双向对称的均值溢出，相比之下，美国对中国的溢出效应程度要强一些。关于趋势项的研究则发现，仅支持美国对中国的单向均值溢出，而两国存有双向波动溢出的结论，无论是从低频分量还是趋势项都可以得到证实。需要特别说明的是，作者曾在经济机理分析的基础上实证检验了中国、欧盟及美国政府债券的相互影响作用，结果发现中美之间存在双向波动溢出但不存在均值溢出[8]。该结论同本文结果显然有所不同，原因固然可以从研究时限不一致从而经济背景及金融市场发展现状各异来加以解释，但决不能忽视甚至更多归因于对原始数据的处理方面，结论的不同显然支持了EEMD方法的有效性。这也提醒相关的后续研究需要重点考虑：从基于结构分解的数据出发所进行的实证分析很可能导致与传统研究不一样的结果。

五、结 论

本文对2008年1月2日-2015年1月2日的中美国债指数进行总体经验模态分解，提取了三个不同频域的结构分量，从均值、相关系数及方差占比判断出低频分量及趋势项能更准确有效地反映两国国债市场的走势。基于该结构分解，选择低频分量及趋势项为研究出发点，从均值及波动两个层面建立了二元VAR-GARCH-BEKK模型，分别考证了中美国债间的溢出效应，研究发现：在重大事件及经济政策的冲击下，两国国债具有程度不对等的双向均值溢出，其中美国对中国的溢出效应较强，而两国间的波动溢出则是对称的；去除“噪声”的影响，从国债市场长期稳态本质的角度看，两国国债市场表现为双向的波动溢出，但均值方面仅存在美国对中国的单向溢出。总体上来说，美国国债对中国国债具有显著影响。

平稳坚实的经济环境，尤其是金融市场，对中国现阶段的经济转轨至关重要。本文结果表明，美国国债市场对中国国债市场具有显著的溢出效应，因此，为了提高国债市场抗风险能力，以保证中国资本市场的健康发展，下面从完善自身发展和加强外部监管两个方面提出如下政策建议：

（一）完善自身交易机制

第一，中国现有债券市场存在银行间与交易所两个交易市场，二者在托管人及交易方式等方面区别较大，大量的投机资本自然会挖空心思来攫取制度分割背后的套利机会，从而不可避免的引起市场的动荡，因此需尽快破除银行间及交易所债券市场间割裂的交易机制，促进两市的互联融合，从而压缩不合理的投机与套利空间，这可以从进一步取消两市间的市场准入限制、扩大市场参与主体及增加跨市场交易品种等入手；第二，虽然近年来中国债券市场有了长足发展，但相比庞大的经济总量，国债规模并不高，尤其远低于发达国家，国债支持实体经济建设的基础性作用还有待进一步发挥，因而需结合中国目前的实际国情不断丰富与创新国债交易品种，以提升市场交易规模，在促进国债作用发挥的同时增强国债市场的抗风险能力。

（二）加强外部有效监管

尽管金融自由化与全球化越来越为人们所关注，但对于新兴市场国家来说，在没有做好充足的抵御外部系统性风险的准备时，加强有效的金融监管仍极其重要，这从近年来国际金融危机传播与蔓延的规律及其对发展中国家的严重冲击后果可以看出。因此，在现阶段，中国不能因为追求资本市场的国际融合而在短期内绝对放松对国债市场的管制，面对日益增多的国际资本尤其是美国巨额游资的涌入，在合理引导以有效补充市场流动性的同时，更要防范及避免其对债券市场的直接冲击，并且需及时出台对冲措施以减小突发事件引致美债变化对中国市场的影响。

西安交通大学金禾经济研究中心侯玉琳同学对本文提供了部分数据支持，在此特表谢意。

[1] 陈守东，韩广哲，荆伟.主要股票市场指数与中国股票市场指数间的协整分析[J].数量经济技术经济研究，2003（5）.

[2] 韩非，肖辉.中美股市间的联动性分析[J].金融研究，2005（11）.

[3] 陈潇，杨恩.中美股市杠杆效应与波动溢出效应[J].财经科学，2011（4）.

[4] 游家兴，郑挺国．中国与世界金融市场从分割走向整合——基于DCC-MGARCH模型的检验[J]．数量经济技术经济研究，2009（12）．

[5] 西村友作．中美两国股票市场联动性研究——基于CCF检验法的新证据[J]．经济评论，2009（2）．

[6] 张兵，范致镇，李心丹.中美股票市场的联动性研究[J].经济研究，2010（11）.

[7] Luo W，Brooks R，Silvapulle P．Effects of the Open Policy on the Dependence between the Chinese‘A’Stock Market and Other Equity Markets: An Industry Sector Perspective[J].Journal of International Financial Markets，Institutions & Money，2011（21）．

[8] 冯涛，刘伟．中国、欧盟与美国债券市场溢出效应研究——欧债危机背景下国债收益率的视角[J].西安交通大学学报:社会科学版，2013，33（4）.

[9] 李成，王彬，黎克俊.次贷危机前后中美利率联动机制的实证研究[J].国际金融研究，2010（9）.

[10]刘威，吴宏.中美两国利率与汇率相互影响效应的评估研究——基于抛补利率平价理论的实证检验[J].世界经济研究，2010（2）.

[11]王晓芳，王瑞君.总体经验模态分解视角下的PPI与CPI波动特征及传导关系研究[J].数量经济技术经济研究，2013（5）.

[12]Huang N E，Shen Z ，Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Process of the Royal Society of London，1998（3）.

[13]Huang N E，Wu M L，Qu W，Long S R，Shen S P.Applications of Hilbert-Huang Transform to Non-stationary Financial Time Series Analysis[J].Applied Stochastic Models In Business And Industry，2003,19（3）.

[14]Wu Z H， Huang N E.Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis，2009（1）．

[15]Peel M C，Amirthanathan G E，Pegram G G S，McMahon T A，Chiew F H S.Issues with the Application of Empirical Mode Decomposition [C].MODSIM05-International Congress on Modeling and Simulation: Advances and Applications for Managem，2005.

[16]李仲飞，肖仁华，杨利军.基于集合经验模态分解技术的中国房地产周期识别研究[J].经济评论，2014（4）.

（责任编辑：张治国）

“第三届金融与计算论坛”会议简讯

2015年7月18日至19日，天津财经大学数学经济研究中心主办的“第三届金融与计算论坛”会议在天津财经大学举行，来自美国、澳大利亚、加拿大、俄罗斯、日本的多位外国专家学者及来自中国科学院、中国社科院、清华大学、北京大学、中国人民大学、中央财经大学、同济大学等单位的专家学者100余人参加了会议。

“论坛”由中央财经大学统计与数学学院、中国科学院计算机网络信息中心超级计算中心、中国数学力学物理学高新技术交叉研究学会及金融量化分析与计算专业委员会协办，并得到了北京聚源锐思数据科技有限公司和北京并行科技有限公司的支持。会议对计算与金融研究的前沿问题和最新研究成果进行了研讨。

（天津财经大学数学经济研究中心 孙杨）

Research on Spillover Effect of Government Bonds between China and USA：Based on Ensemble Empirical Mode Decomposition

YAN Shu-xi1，LIU Wei2

（1.School of Mathematics and Statistics, Yulin University, Yulin 719000，China；2.School of Economics and Finance，Xi'an Jiaotong University，Xi'an 710061，China）

The ensemble empirical mode decomposition is an internationally recognized method which can process non-stationary and nonlinear time series effectively.In the context of Sino-US convergence, this paper firstly decomposes the Sino-US Treasury bond index with EEMD, and filter out low frequency components and trends respectively which can represent the original time series exactly.Then it builds the VAR-GRACH-BEKK model to verify spillover effect of government bonds exist or not between China and USA from the mean and volatility.The results show as follows: when unexpected events occur and economic policies change, bilateral mean spillover effect exists, but the extent is not symmetrical, US' bond spills over into China's strongly, while volatility spillover effect is symmetric.In the long process of government bond's intrinsic development, volatility spillover effect is symmetric, but mean spillover effect exists from US to China unidirectionally.China should further improve the bond market trading mechanism, rich the government bond's varieties, and strengthen financial market regulation, so as to hedge the spillover effect from US to China effectively, prevent and mitigate the systemic risk.

ensemble empirical；mode decomposition；government bond；spillover effect

2015-02-26；修复日期：2015-05-22

闫树熙，男，陕西榆林人，硕士，讲师，研究方向：社会经济与金融统计； 刘 伟，男，陕西富平人，博士生，研究方向：国际经济与投资，货币与财政政策。

F830.9

A

1007-3116（2015）09-0027-09