一堂数学实验课的思考

☉江苏省淮阴中学新城校区 孙立章

一堂数学实验课的思考

☉江苏省淮阴中学新城校区 孙立章

一、对数学实验的认识

数学实验是学生运用有关工具（如纸张、剪刀、测量工具、作图工具以及计算机等），通过动手、动脑“做”数学的一种数学学习活动.数学实验过程中学生不是被动地接受课本上的现成结论，而是从自己已有的数学经验出发，通过动手、动脑去获得新的数学经验，逐步构建并完善、发展自己的数学认知结构.数学实验课的活动设计要步骤明确，层次清楚，可操作性强，老师要引导学生对实验活动的过程与结果进行思维加工，概括提炼.学生的创新思维往往来自学习过程中的偏差与好奇心，而数学实验恰恰可给学生提供探索发现、猜想验证的机会，恰当引导，让学生通过自身的实践真切感受到发现的快乐，在实验过程中学会思考，学会创新.

二、一堂数学实验课的内容概述

一堂“分割纸片”数学实验课，其主要内容如下所示.

实验准备：正方形纸片若干张.

实验内容与步骤如下所示.

（1）我们可以将一张正方形纸片按如图1所示的方式分解成4张正方形纸片（其边长可以相等，也可以不等）.你能将一张正方形纸片分割成n（n＜10）张小正方形纸片吗？试试看，并与同伴交流.

（2）你能将一张正方形纸片分割成5张小正方形纸片吗？试解释原因.

（3）你能将一张正方形纸片分割成n（n≥10）张小正方形纸片吗？n的取值会受限制吗？说说理由，并提供n= 2015时的分割方案.

三、关于这节数学实验课的思考

1.实验步骤的细化

“课标”要求：实验中步骤的设计应从学生的实际出发，由浅入深，抓住关键，阶梯式地逐渐提升，让学生在逐步解决问题的过程中体会其中蕴含的数学思想与方法.

洒布材料选用AH—70号热沥青，用量为1.6kg/m2，然后再洒布一层经拌和站加热除尘的石灰岩石屑，其厚度为0.5cm，粒径为0.5～1.0cm，其中掺加0.4%沥青。下封层洒布采用智能碎石洒布车及智能沥青洒布车进行洒布。并用胶轮压路机进行碾压。

“分割纸片”这节课，所安排的实验步骤起点较高，难度、跨度都偏大，且不利于学生操作，可以细化成以下几个小步骤.

步骤1：“我们知道一张正方形纸片无法分割成2张或3张正方形纸片，你能将一张正方形纸片分割成4张小正方形纸片吗？”作为本课的第一个实验，简单易行（如图1），容易调动起学生的热情，但它是本节课研究的起点.

步骤2：“你能将一张正方形纸片分割成6张、7张小正方形纸片吗？”这一步具有一定的挑战性，给学生自主探究、小组合作均提供了足够的空间.其中分割成6张如图2所示，分割成7张如图3所示.

步骤3：“你能将一张正方形纸片分割成8张、10张小正方形纸片吗？”分割成8张如图4所示；分割成10张分法多样，如图5、图6所示.比较发现：分割成4张、6张、8张、…类似，归纳成一般情况：只要分割成2n（n是大于或等于2的整数）张，均可用同样的分割方法；分割成4张、7张、10张、…类似，归纳成一般情况：只要分割成3n+1（n是大于或等于1的整数）张，均可用同样的分割方法.这一活动旨在引导学生积累活动经验，向发现规律迈出最重要的一步，实现直观感受向理性思考的过渡.

图1

图2

图3

图4

图5

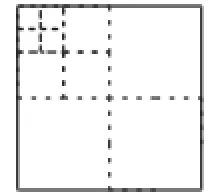
图6

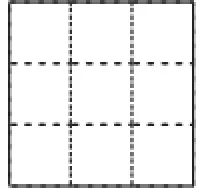
图7

图8

步骤4：“你能将一张正方形纸片分割成9张小正方形纸片吗？”学生首先会画出图7，也有学生会画出图8，但不管哪种都可以看成是前两类分割方法的组合应用.这一步骤促进学生由“做”向“思”的进一步转变，推动学生实现思维的飞跃.

步骤5：“你能将一张正方形纸片分割成5张小正方形纸片吗？”通过分析感受“分割成5张小正方形纸片”的不可能性，通过归纳、猜想等理性分析手段，得到一张正方形纸片的可分割规律.

2.分割方法的概括、分类

数学实验中，应注重直观，使在实验过程中所研究的内容“可视化”，让学生从中获得对数、形的理解，并逐步对其适度抽象，进行更高层次上的再实验，进而体会数学的研究方法，使学生在活动中认识并改造自己的数学知识结构.

纸片分割过程中发现，共有3类分割方法，为了实验探究的方便，增加学生的“可视化”效果，可以根据图形的特征进行形象化的概括，使分类更加明确，一目了然.

比较发现：分割成4张、6张、8张后的图形（如图1、2、4）类似，我们可以形象地称之为“L”型分割，归纳成一般情况：只要分割成2n（n是大于或等于2的整数）张，均可用“L”型分割；分割成4张、7张、10张后的图形（如图1、3、5、6）类似，我们可以形象地称之为“田”型分割，归纳成一般情况：只要分割成3n+1（n是大于或等于1的整数）张，均可用“田”型分割；分割成9张小正方形纸片过程中，学生首先会画出图7，也有学生会画出图8，但不管哪种都可以看成是在“L”型基础上增加一个“田”型，我们可以形象地称之为组合型.

3.分割结论的进一步探讨

课堂上对正方形纸片的分割当然不可能探究得太深入，但数学实验会唤醒学生的主体意识，激发学生的好奇心和兴趣，课后还可以引导学生进行更深入的研究，让学生真正理解数学的本质，体会数学知识的博大精深和相互联系，形成新的数学模型.

进一步研究正方形纸片的分割，发现“田”型、“L”型、组合型三种分割模式的规律可以统一为一个代数式：3m+2n+4（m≥0，n≥0）.

对代数式3m+2n+4（m≥0，n≥0）做以下几点说明.

（1）当m=0时，3m+2n+4=2n+4.n=0、1、2、3、…时，2n+ 4=4、6、8、10、…，即“L”型分割模式；

（2）当n=0时，3m+2n+4=3m+4.m=0、1、2、3、…时，3m+4=4、7、10、13、…，即“田”型分割模式；

（3）当m≠0，n≠0时，即组合型分割模式.

联系课堂“将一张正方形纸片分割成2015张小正方形纸片”的组合型分割方法的研究，3m+2n+4=2015即3m+2n=2011，因此二元一次方程3m+2n=2011的所有正整数解就是“将一张正方形纸片分割成2015张小正方形纸片”的所有分割方法.这是一个由数到形再到方程的模型转换.

4.分割对象的变化

本课的分割对象是“正方形”，我们还可以将“正方形”变成“正三角形”.与分割正方形纸片相比，分割正三角形纸片，虽然是不同的图形，但它们具有同样的特征（各边相等），可以用相同的探究思路，得到一个类似的结论.教师可以引导学生通过类比、联想，依据分割“正方形纸片”的方法和思路来研究分割“三角形纸片”，实现实验对象的创新.Z