初中数学“五步归一”错例修正法的实践与探索——以一道作业本习题为例

☉浙江省余姚市教育局教研室应建军

初中数学“五步归一”错例修正法的实践与探索
——以一道作业本习题为例

☉浙江省余姚市教育局教研室应建军

一、相关概念

1.错例修正

通过师生合作对学生在平时作业、考试试卷中存在的错例进行订正、分析及反思，以获取正确或合理的做法并进行思维的拓展，从而提高教学活动的有效性.

2.初中数学“五步归一”错例修正法的基本模式

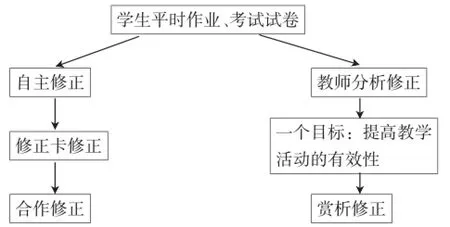
3.初中数学“五步归一”错例修正法的基本步骤

第一步，自主修正：学生针对平时作业、考试试卷中的错例进行订正，不明之处请教同学或老师，争取及时修正错例.

第二步，教师分析修正：教师整合学生在平时作业、考试试卷中的错例后进行系统的讲解、比较及适当拓展，学生在教师的分析过程中修正错例.

第三步，修正卡修正：学生通过整理、归类、筛选，把典型的错例摘抄或剪贴在错例修正卡中，并写出错误原因、正确的解法、反思与拓展，从而修正错例.

第四步，合作修正：教师安排定量时间组织学生互相学习、评析错例修正卡，并推选优秀错例分析供交流学习，学生在小组合作过程中修正错例.

第五步，赏析修正：教师根据各组推选的错例分析进行核查、筛选，最终确定优秀作品，贴于教室的“作品栏”，学生在欣赏作品的过程中修正错例.

一个目标：提高教学活动的有效性.通过实施上述五个错例修正步骤完备学生知识，学生对知识掌握过程中存在的问题进行思考，改正学生解题过程中的错误习惯、错误做法，培养学生的辨析错误能力、创新思维能力，增强学生学习数学的信心，从而提高教学活动的有效性.

二、实施“五步归一”错例修正法的典型案例

一道作业本习题的修正过程：

例1（浙教版数学八年级上册配套作业本第二章复习题第16题）如图1，直角三角形纸片的两直角边AC=6cm，BC=8cm，现将直角边AC沿AD折叠，使它落在斜边AB上，点C与点E重合，求CD的长.

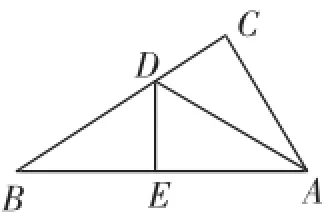
图1

此例是一道代数与几何结合的综合性题目，涉及勾股定理、折叠问题、一元二次方程等知识，应用了转化、方程、数形结合等数学思想，具有一定的灵活性、创新性.

第一步，自主修正.

学生针对平时作业、考试试卷中的错例进行订正，不明之处请教同学或老师，争取及时修正错例.学生对此例的主要订正过程如下：

解析：由已知折叠可知∠AED=∠C=90°，AE=AC= 6cm，DE=CD.因为BC=8cm，所以AB=10cm，所以BE=4cm.

在Rt△BED中，BE2+DE2=BD2，即42+CD2=（8-CD）2，解得CD=3cm.

很多学生不会订正这一题，共有5个学生问了老师，有些学生在同学之间也进行了探讨、请教.

第二步，教师分析修正.

此例是一道典型的错例，A老师在作业讲评过程中进行了重点分析，分析过程如下：

首先，此例要在折叠过程中找到不变的量，即∠AED=∠BED=∠C=90°、AC=AE、DC=DE.其次，运用转化思想把问题转化到Rt△BED中，然后根据勾股定理得到BE2+DE2=BD2，再利用方程思想得到关于线段CD的一个一元二次方程，最后，解此一元二次方程得到CD= 3cm.为了更好地使学生理解和巩固本题的思想方法，提高学生求解这类几何图形中的线段长度问题，对此题进行了变式拓展.

变式1：如图2，将长方形ABCD沿AE对折，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EC的长.

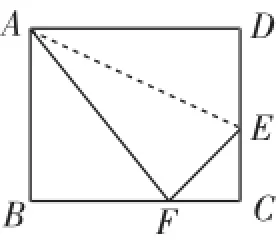
图2

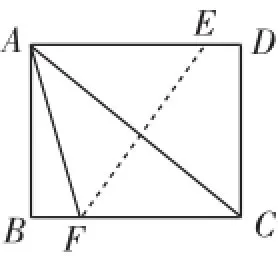
图3

变式2：如图3，将长方形ABCD沿EF对折，使顶点A与顶点C重合，已知AB=8，BC=6，求折痕EF的长.

第三步，修正卡修正.

图4是学生修正卡的缩略图，学生将自认为最典型的错例写在或剪贴在修正卡中，学生通过分析错解原因、写出正确解答、针对错例进行反思及拓展，每人每周至少完成两份.

图4

实验班共有7个学生对此例进行了错例分析.

学生分析的错解原因主要有：没运用对折重合的性质；知道对折重合对应边相等、对应角相等，但不知道有什么用处；没想到转化到Rt△BED中去求；没想到可以列方程解几何题.

学生分析的反思或拓展主要有：有些几何图形尤其是在直角三角形中可以根据勾股定理列方程；应注意折叠问题中的“变中求不变”；应掌握对折重合的性质，运用勾股定理求线段的长；有两位学生将老师的变式题抄在了修正卡中；有一位学生编写了一道变式题，将题中的数字改了一下，把AC改成了3cm、BC改成了4cm；有一位学生编写了一道变试题：如图1，直角三角形纸片的两直角边AC=6cm，BC=8cm，现将△ABC沿DE折叠，使得点B与点A重合，求CD的长.

第四步，合作修正.

教师将整个班级42人分成7组，确定一位学生为合作小组组长，由组长负责安排小组内成员互相学习、评析一周内完成的错例修正卡，在每周四的习题课中安排20分钟时间进行小组合作修正错例，学生对完成的修正卡进行互相学习、评析，每小组推选2～4道优秀错例分析供班级交流学习，有两个小组均推选了此例的分析.

第五步，赏析修正.

教师根据各组推选的错例分析进行核查、筛选，其中学生甲对此例的分析作为优秀作品贴于教室的“作品栏”，学生在欣赏作品过程中修正错例.

三、初中数学“五步归一”错例修正法的实践意义

通过实践发现“五步归一”错例修正法的实施对提高教学活动的有效性起到了积极的作用，归纳如下：

1.充分发挥学生主体的作用

古人云“疑者觉悟，觉悟之机也；一番觉悟，一番长进”，学生对错例的修正不能光靠教师的讲解和不断的强化，其更好的途径是发挥学生的主体作用，进行反思质疑，从而提高错例修正的效果.错题能够暴露学生在学习过程中的不足，是学生提高成绩最有价值的反馈信息，通过对错例的自主修正，学生能自我发现错例的错误原因，得到正确解答，从而更加有效地掌握基础知识和基本技能.针对典型错例进行自主修正、反思与拓展、小组合作修正等过程，给学生搭建了积极思考、合作交流的平台，充分发挥了学生的主体作用.当自己的错例分析在同学之间互相传阅、互相学习时，每个学生都会倍感激动，都想在此时得到同学的认可，因此，学生的表现尤为积极，激励了学生更加认真地进行错例分析.

2.提高学生辨析、修正错例能力

通过“五步归一”错例修正法的实践后发现，学生辨析、修正错例的能力得到了提高.如学生乙平时成绩不佳，但在考试过程中对测试题2的错解进行了自我修正，一开始他选择了B，在考试结束之前对此题进行了检查，发现折痕EF的长必定大于AB的长，不该选择B，因此重新读了题目，后来通过构造直角三角形利用勾股定理算得EF=故选择了A，考完后他激动而自信地对笔者说：“老师，第9题答案是不是A啊！这一题我本来是解错的，后来考虑了一下发现有点不对劲，重新读了题目后发现自己解错了，我在最后3分钟内把它做了出来”，听到甲同学的这句话笔者感到无比的欣慰，学生能进行自我反思、自我发现问题、自我修正，这是多么难能可贵啊！

3.培养学生创新思维能力

学生对典型错例进行反思与拓展能充分挖掘学生的潜能，培养学生的创新思维能力.学生对一道错例进行反思，思考为什么错、该怎么做、还能怎么做、应注意什么等问题后能获得正确解答问题的途径，总结问题解决的方式和方法.学生对错例进行拓展，编写变式题或进行类比能引起学生积极思考，提高创新思维能力.学生甲把典型错例进行了变式拓展，原图不变，原来“将直角边AC沿AD折叠，使它落在斜边AB上，点C与点E重合”改为“将△ABC沿DE折叠，使得点B与点A重合”，仍然求CD的长，考查的知识和解题的思路基本不变，但折叠方法改变了，问题的焦点转移到了△ACD中，充分表明学生对此例进行了积极的思考、深刻的理解及灵活的运用，展现了学生具有较强的创新思维能力.H