混凝土收缩模型相对湿度修正值对比

张贤文

(益阳市交通规划勘测设计院，湖南 益阳 413000)

0 引言

不同湿度环境下混凝土结构变形存在较大差异，同时钢筋的存在对结构的变形和应力发展也将产生巨大影响，在对结构和构件的长期变形进行分析预测时必须对湿度和配筋的影响作用有充分的认识。

加载龄期和加载持续时间是决定徐变系数的两个重要因素，一般将徐变系数中这两个时间函数的表达式作为徐变系数数学表达式的特征式，目前国内外收缩应变预测模型大多采用乘积模式，模型中一部分是影响因素对收缩应变发展的修正系数，一部分是收缩应变随时间发展的函数关系。预测模式主要根据对大量的试验数据分布现象进行观察和研究，构造出如双曲函数、幕函数、指函数类的预测公式;或以理论分析为基础，建立预测模式的框架，根据试验数据回归确定参数［1，2］。

混凝土的徐变往往是造成大跨度预应力混凝土桥梁在长期运营后预应力损失、长期变形和内力重分布显著增加的一个主要原因，得到设计人员的高度关注［3－6］。本文通过对中国建科院模型、CEB—FIP 模型、ACI—209 模型等研究，对比了国内外收缩应变预测模型影响因素取值差异性，对提高对混凝土收缩影响因素修正值把握，对实际桥梁结构效应分析中混凝土收缩应变模型选取至关重要。

1 国内外常见收缩应变模型计算式

1.1 中国建科院收缩模型(1986)

中国建科院模型(1986)收缩应变计算模型表达式中，主要有影响混凝土收缩的影响系数和混凝土收缩应变的时变函数相乘，具体的混凝土收缩应变ε(t)表达式如下:

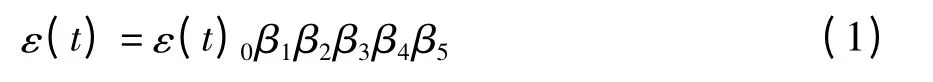
其中:普通混凝土中:

轻骨料混凝土中:

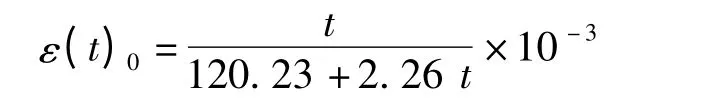
式中:ε(t)0为普通混凝土或轻骨料混凝土收缩基本方程;β1为环境相对湿度对混凝土收缩的影响系数;β2为构件截面尺寸对混凝土收缩的影响系数;β3为养护方法对混凝土收缩的影响系数;β4为粉煤灰取代水泥量对混凝土收缩的影响系数;β5为混凝土强度等级对混凝土收缩的影响。

1.2 CEB－FIP(1990)收缩模型

CEB—FIP(1990)收缩应变计算模型中采用了乘积模式，乘积模式由名义收缩系数和混凝土收缩时变函数两部分组成，在第一部分为名义收缩系数中，即为混凝土收缩应变终值，它由水泥种类、混凝土强度等级和环境年平均相对湿度决定;第二部分为混凝土收缩变形时变函数，它是由计算考虑时刻混凝土龄期t 和构件理论厚度决定，具体混凝土收缩应可按下列公式计算:

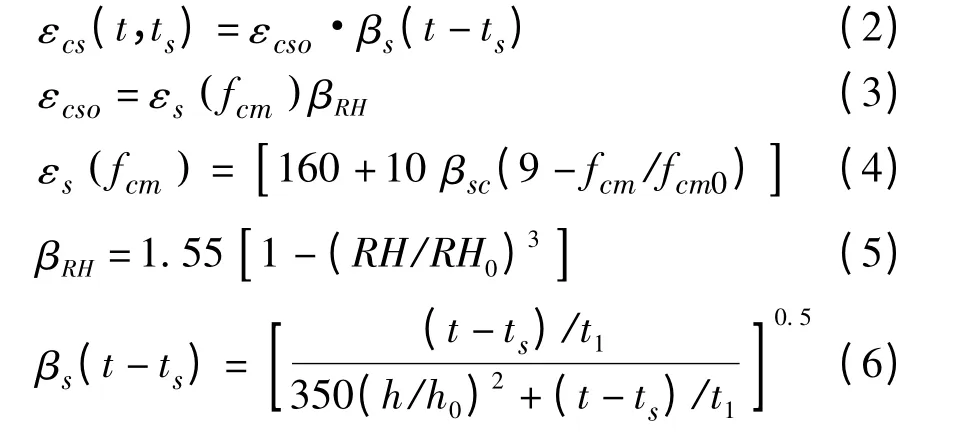
式中:t 为计算考虑时刻的混凝土龄期，d;ts为收缩开始时的混凝土龄期，d，可假定为3 ～7 d;εcs(t，ts)为收缩开始时的龄期为ts，计算考虑的龄期为t 时的收缩应变;εcso为名义收缩系数;βs为收缩随时间发展的系数;fcm为强度等级C20 ～C50 混凝土在28 d 龄期时的平均立方体抗压强度，MPa;fcm=为龄期为28 d，具有95%保证率的混凝土立方体抗压强度标准值，MPa;βRH为与年平均相对湿度相关的系数，式(5)适用于40%≤RH≤90%;RH 为环境年平均相对湿度，%;βsc为依水泥种类而定的系数，对一般的硅酸盐类水泥或快硬水泥，βsc=5.0;h 为构件理论厚度，mm;h=2A/u，A 为构件的截面面积，u 为构件与大气接触的周边长度;RH0=100%;h0=100 mm;t1=1 d;fcm0=10 MPa。

1.3 ACI—209 收缩模型

在ACI—209 规范中，收缩应变计算模型与中国建科院收缩应变模型结构相似，采用的为乘积模式，其中混凝土收缩应变计算公式为:

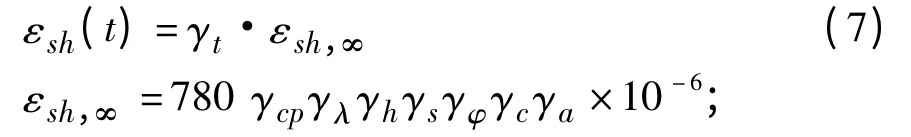
式中:εsh，∞为收缩应变终值;γt为持续时间影响系数;γcp为初始养护条件校正系数，潮湿养护天数为1、3、7、14、28、90 时，γcp分别取值为1.2、1.1、1.0、0.93、0.86、0.75;γλ为环境相对湿度校正系数，γλ=1.40－0.01 λ(40≤λ≤80)，γλ=3.00－0.03λ(80 ＜λ≤100)，其中，λ 为环境相对湿度，%，当λ ＜40，γλ＞1;γh为平均厚度校正系数，γh=1.2 e－0.00472V/S，V/S 为体积面积比，mm;γs为混凝土稠度影响系数(当坍落度为S mm 时，取0.89+0.001 62S);γφ为细集料含量影响系数(当粒径小于4.8 mm，细集料含量百分比F ＜50%时，取0.3+0.14F);γc为水泥含量影响系数(水泥含量C kg/m3时，取0.75+0.000 61 C);γa为空气含量影响系数(当空气含量为A%时，取0.95+0.008A≥1，常取1)。

1.4 GZ(1993)收缩模型

在GZ(1993)收缩应变模型中，预测模型表达式如下:

式中:h 为环境相对湿度，以小数表示;t 为混凝土计算龄期，d;tc为混凝土开始干燥时的龄期，或者混凝土潮湿养护结束时的龄期，d;K 为与水泥类型有关的系数，对I 类水泥取1.0，对Ⅱ类水泥取0.70，对Ⅲ类水泥取1.33;V/S 为混凝土构件体表比，mm;为混凝土干燥时的平均抗压强度，为混凝土龄期为28 d 时的平均抗压强度，MPa。

1.5 GL(2000)收缩模型

在GL(2000)收缩应变模型中，预测模型表达式如下:

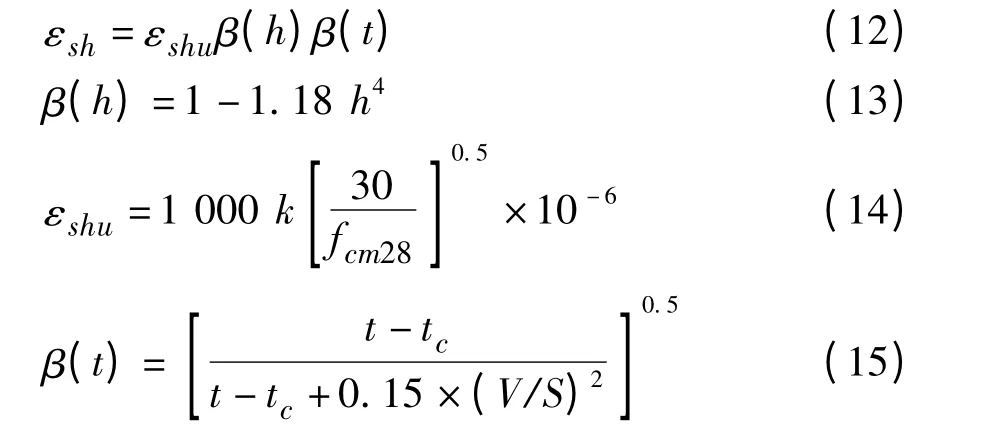
式中:h 为环境相对湿度，以小数表示;t 为混凝土计算龄期，d;tc为混凝土开始干燥时的龄期，或者混凝土潮湿养护结束时的龄期，d;K 为与水泥类型有关的系数，对I 类水泥取1.0，对Ⅱ类水泥取0.70，对Ⅲ类水泥取1.33;V/S 为混凝土构件体表比，mm;为混凝土龄期为28 d 时的平均抗压强度，MPa。

2 环境年相对湿度修正值对比

周围介质的相对湿度对混凝土的收缩有显著的影响。湿度愈大，吸附水的蒸发量愈小，水泥的水化程度愈高，水泥凝胶体的密度也愈高，收缩变形也愈小。在中国建科院模型中，环境相对湿度对混凝土收缩影响系数(β1)采用表格形式来描述不同年环境相对湿度下β1取值，具体见表1。

表1 环境相对湿度对混凝土收缩影响系数

在ACI—209 模型中，环境相对湿度对混凝土收缩影响系数采用方程式来描述不同年环境相对湿度下环境相对湿度校正系数，详见下式:

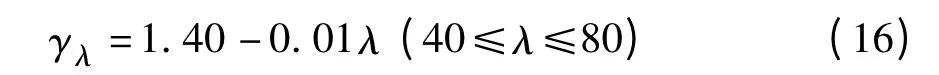
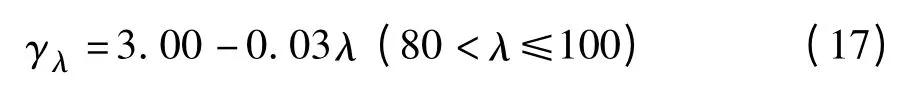
其中，λ 为环境相对湿度，%，当λ ＜40，γλ＞1。

在CEB—FIP(1990)模型中，环境相对湿度校正系数计算公式如下:

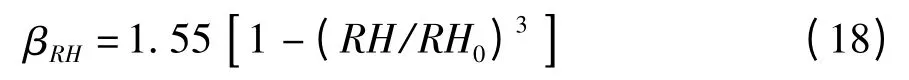
在GZ(1993)收缩模型中，环境相对湿度校正系数计算公式如下:

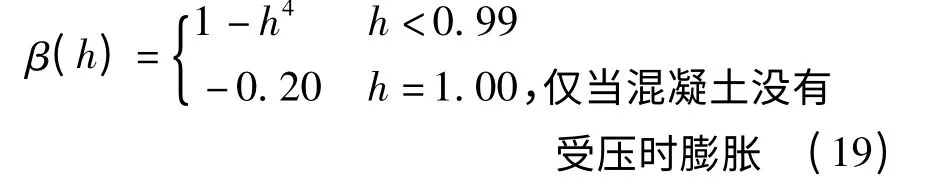
在GZ(2000)收缩模型中，环境相对湿度校正系数计算公式如下:

通常情况下，环境年相对湿度在40%～80%之间，为了对比不同预测模型中年环境相对湿度对收缩徐变影响，以环境年相对湿度10%变化等级，将各个计算模型中环境相对湿度校正系数在不同环境年相对湿度下进行取值绘图，其中，中国建科院模型中环境相对湿度对混凝土收缩影响系数采用直线内插，见表2 所示。

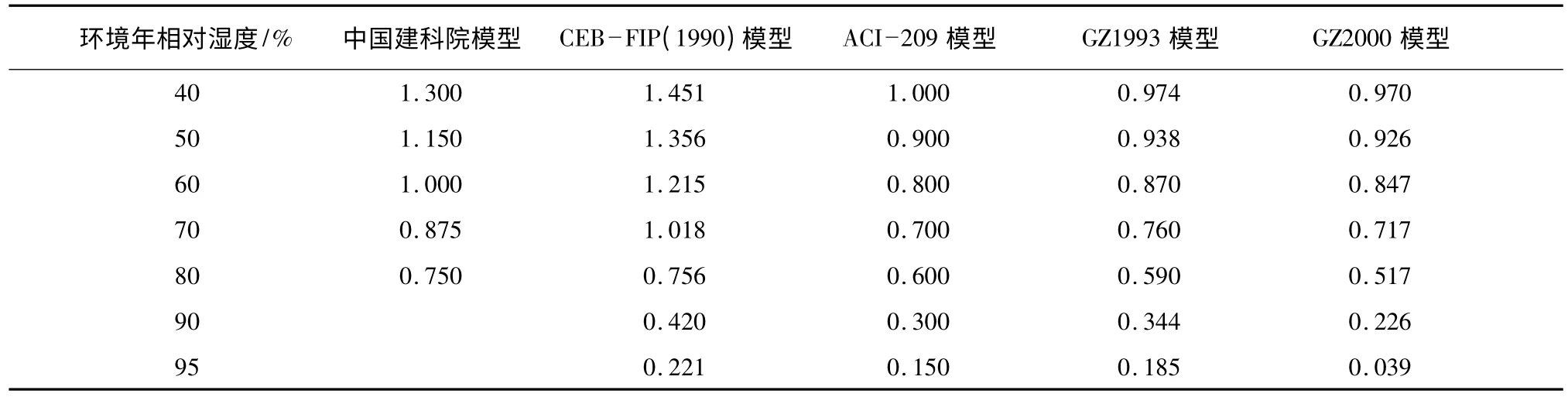
表2 不同预测模型年环境相对湿度取值

由表2 可知，不同预测模型年相对湿度修正值相差较大，其中中国建科院模型年环境相对湿度修正系数与CEB—FIP(1990)很贴近，但中国建科院模型没有提供环境相对湿度在80%以上取正值，中国建科院模型在年环境相对湿度为60%情况下修正值为1，CEB—FIP 模型在年环境相对湿度为70%情况下修正值约为1，且这两个模型皆被国内规范和工程实际人员所采纳。国外收缩应变计算模型中年环境相对修正值很贴近，在年环境相对湿度为40%情况下修正值接近于1，但在年环境相对湿度为40%～80%修正值与国内规范采纳修正值相差较大。

为了更加形象对比国内外模型年环境温度相对湿度修正值之间关系，将各预测模型年相对湿度与修正值之间关系见图1。

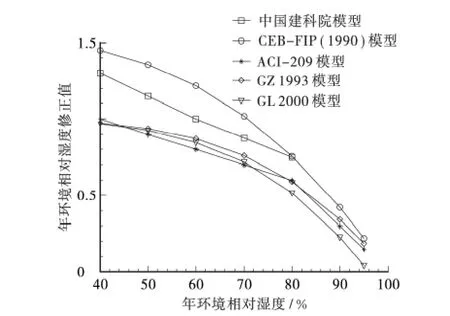
图1 各预测模型年相对湿度修正值之间关图

由图2 可知，中国建科院模型和CEB—FIP(1990)模型年相对湿度修正值高于国外收缩应变预测模型修正值，在年环境相对湿度为40%～70%之间相差最大，在年环境相对湿度大于70%时，逐步与国外年湿度修正值靠近，而国外不同模型间年相对湿度修正值十分贴近，且关系曲线图发展趋势基本一致，关系曲线变化率逐步增大，说明混凝土收缩变形速率随着年环境相对湿度减小而逐步减小。

曾有学者张智博［7］通过采用饱和盐溶液方法形成不同的相对湿度环境，研究了混凝土干缩值与环境相对湿度之间的关系。结果表明:混凝土的干缩受环境相对湿度影响显著，环境相对湿度越低，其干缩值越大，混凝土干缩值与环境相对湿度之间的关系不成线性比例。文献［8］对国内外收缩徐变模型中湿度影响作用进行了分析，通过实验研究了不同湿度下(60%、75%、90%)混凝土收缩特性，详见图2。现在将本文研究预测模型不同湿度下变形比值与文献［8］进行比较，进行综合排名，不同湿度环境试件的收缩变形对比见表3。

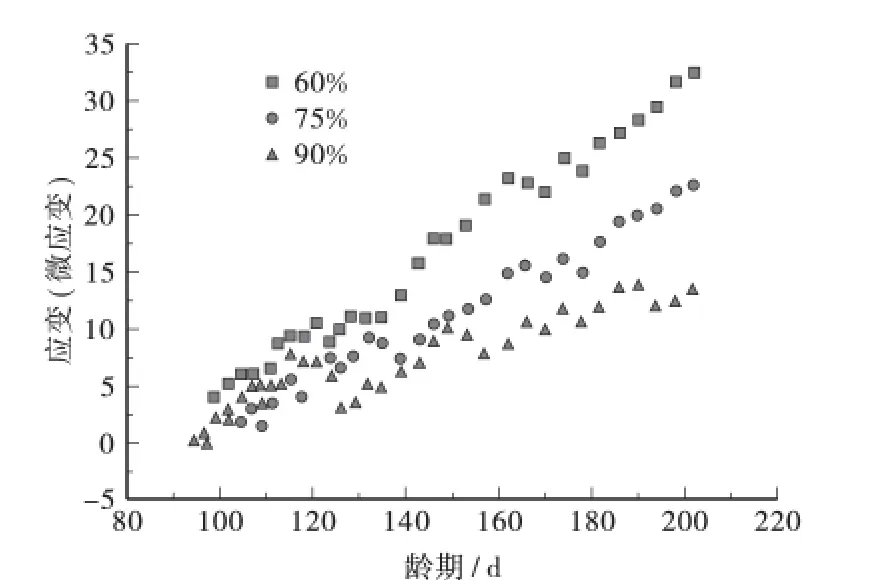
图2 不同湿度条件下混凝土试件的收缩变形

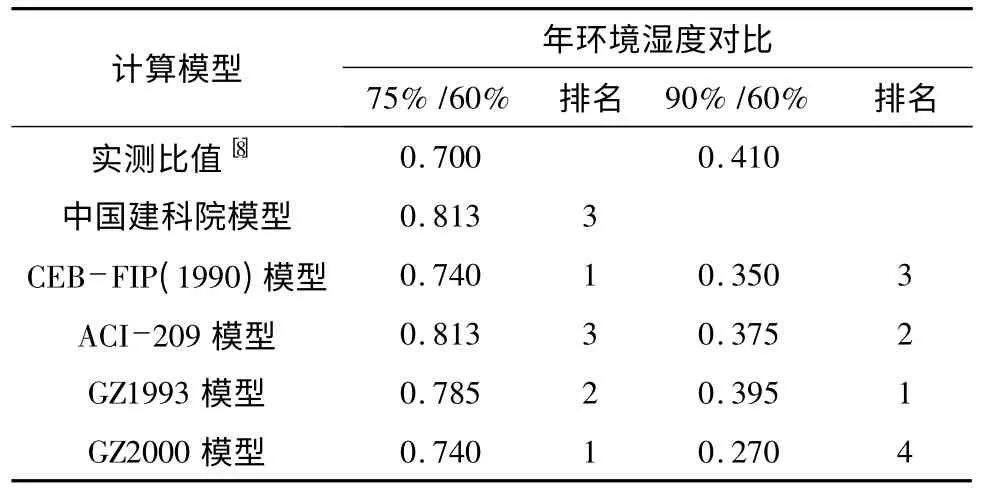
表3 不同湿度环境试件的收缩变形对比

由表3 可知，国内外收缩应变模型中年湿度收缩变形修正比值与实测年环境湿度比值为(75%/60%)实测比值普遍偏大，与实测环境年湿度比值为(90%/60%)比值普遍偏小。从整体排名而言，计算效果较好的是GZ1993 模型中环境年相对湿度修正值。

3 结论

通过对国内外收缩应变模型中环境年相对湿度修正值的对比，可得到如下结论:

1)中国建科院模型和CEB—FIP(1990)模型年相对湿度修正值高于国外收缩应变预测模型修正值，在年环境相对湿度为40%～70%之间相差最大，在年环境相对湿度大于70%时，逐步与国外年湿度修正值靠近。

2)国内外收缩应变模型年环境湿度修正值与年湿度相对值(%)关系曲线图发展趋势基本一致，关系曲线变化率逐步增大，说明混凝土收缩变形速率随着年环境相对湿度减小而逐步减小。

3)就本文而言，通过对比环境年相对湿度修正值与实测值比值差异性，计算效果较好的是GZ1993模型，在国内混凝土构件在非标准养护条件下，建议用GZ1993 模型中年相对湿度修正值进行分析计算。

［1］ACI Committee 209.Prediction of Creep，Shrinkage，and Temperature Effects in Concrete Structures［M］.Houston.Farmington Hills:America Concrete Institute，1992.

［2］张克波，许 康，吕 毅，等.配筋混凝土柱徐变试验［J］.长沙理工大学学报(自然科学版)，2011，8(2):17－20.

［3］余慧平.混凝土徐变与收缩特性现场试验研究［J］.铁道建筑技术，1997(5):7－10.

［4］Committee Euro-International du Beton/Federation International de la Pre constitute.CEB-FIP model code for concrete structures［M］.Switzerland:Thomas Telford，1990.

［5］BAZANT Z P，MURPHY W E.Creep and shrinkage prediction model for analysis and design of concrete structures－model B3［J］.Material and Structures，1995(28):357－365.

［6］吴华君，方鹏飞.高性能混凝土干燥收缩规律研究［J］.混凝土，2009(8)，33－35.

［7］张智博，张 君.混凝土收缩与环境湿度的关系研究［J］.建筑材料学报，2007，9(6):720－723.

［8］郭磊磊.湿度和配筋对混凝土收缩、徐变性能影响研究［D］.哈尔滨:哈尔滨工业大学，2012.