旋转圆柱绕流的流场特性

何颖，杨新民，陈志华，刘波，易文俊

（1南京理工大学瞬态物理重点实验室，南京210094；2淮海工业集团有限公司，山西长治046012）

旋转圆柱绕流的流场特性

何颖1，杨新民1，陈志华1，刘波2，易文俊1

（1南京理工大学瞬态物理重点实验室，南京210094；2淮海工业集团有限公司，山西长治046012）

在亚临界区Re=1.4×105条件下，基于大涡模拟（LES）方法对均匀来流作用下的旋转圆柱绕流进行了数值模拟。通过与非旋转时的实验和计算结果比较，验证了文中计算的准确性。在此基础上，对不同转速条件下（0≤α≤2，α为圆周线速度与自由来流速度的比值）的圆柱绕流进行了数值研究。结果表明，圆柱旋转可以有效地抑制其旋涡脱落，随着转速的增加，可大幅提高其升阻比，主要表现为阻力系数减小而升力系数线性增大。当α=2时，阻力系数和升力系数在经过短暂过渡期后达到稳定。

高雷诺数；旋转圆柱；圆柱绕流

0 引言

圆柱绕流是流体力学的经典课题，且广泛存在于自然界与工程实际中，如高层建筑、烟囱、近海工程结构以及海底管线、架空电缆等。圆柱绕流一般会产生旋涡脱落并诱发流体载荷脉动与结构振动。这主要是因为流体流经障碍物时，由于边界层分别从物体上、下表面分离，在其尾部形成一个负压背风区，随着物体上、下边界层的交替脱落，形成相应的涡街，并对物体产生交变的升阻力，诱发物体振动。涡致振动不仅对物体造成疲劳损伤，当涡脱落频率与物体固有频率相差不大时，还会引起共振，直接对结构造成破坏。另外，旋涡脱落还有增大阻力，产生噪声等危害。

人们出于不同的工程应用目的，对旋涡脱落的抑制进行了很多研究，提出了不少控制方法，如电磁控制[1-2]与圆柱旋转控制[3-9]。以上方法的流体分离控制研究主要集中在低雷诺数情形。如Kang等[3]研究了层流旋转圆柱绕流，发现粘性均匀流中的旋转圆柱可修正尾迹和旋涡脱落，能够降低激流振荡。Ingham等[4]采用有限差分法对雷诺数分别为5和20，相对转速为0～0.5的旋转圆柱绕流进行了数值仿真。Kang[5]对Re=40，60，100，160，相对转速为0～2.5的旋转圆柱绕流进行了数值模拟，得出了60≤Re≤160时流体达到稳定的最大转速。Mittal[6]和Padrino[7]分别对雷诺数为200和200、400、1 000时的旋转圆柱绕流进行计算，分析了升力系数、阻力系数以及压力系数的变化规律。

对于属于亚临界区的高雷诺数圆柱绕流，圆柱尾流涡街转捩为湍流，绕流特性变得复杂，此时圆柱表面分离涡脱落与尾流湍流之间的相互作用关系等仍有待进一步研究。目前，赫鹏等[8]分别对Re=26，200，1.4×105的圆柱绕流进行了二维数值模拟，分析了三种典型雷诺数条件下的绕流形成机理，并得出以空气为介质时的计算结果与实验结果更相符的结论。Isiam等[9]采用LES方法对雷诺数Re=4.2×104，4.6×104，105的二维圆柱绕流进行了计算，验证了LES方法对高雷诺数圆柱绕流模拟结果的准确性。Breuer[10]采用不同网格模型对Re=1.4×105的圆柱绕流进行了数值模拟，发现加密网格并不能得到更准确的结果，而适中的网格与Cantwell等[11]的实验结果则吻合得较好。

而对于亚临界区旋转圆柱的绕流，因其尾流与旋转圆柱相互作用而使整个流场变得更加复杂。初步研究表明，当圆柱旋转速度达到一定值时，圆柱表面的旋涡脱落消失，同时因产生马格努斯力而使升力增加，并且在一定条件下还可能产生负马格努斯力效应。因此，对亚临界区域内的旋转圆柱流场开展研究，揭示其流场与阻力随圆柱转速变化的特性具有非常重要的工程实际意义。

本文选取亚临界区的雷诺数为Re=1.4×105，圆柱转速分别为α=0.5，1.0，1.25，1.5和2.0（其中α=q˙ D/（2u0），为旋转角速度，u0为自由来流速度，D为圆柱半径）进行了数值仿真，对不同旋转速度的升阻力变化情况进行了详细分析，可为其相关工程实际应用提供参考。

1 数值方法与模型

湍流大涡模拟（LES）的基本思想是通过滤波方法将湍流中瞬时脉动运动分解为大尺度和小尺度部分，大尺度运动通过求解可解尺度的N-S方程直接得到，小尺度运动对大尺度的作用则通过亚格子尺度模型来模拟，本文选用Smagorinsky亚格子模型，方程中的对流项采用二阶AUSM格式，关于时间推进则用二阶R-K格式。由于此时圆柱表面仍为层流，尾部湍流区对其气动系数影响较小，因此为了节省计算资源，本文对其作二维数值模拟，并将计算结果与前人的实验与数值计算进行了对比，验证了结果的可靠性。

取计算区域如图1所示，为20D×17D，坐标原点取圆柱中心，沿流向为x方向，阻塞率D/H=1/17，模型上游来流区域为4D，下游尾流区为16D，离上下边界各为8.5D。圆柱第一层网格离壁面距离y=0.01 mm，本文取D=0.1 m，由y+=0.172（y/D）Re0.9可知，y+的值为0.73。经网格收敛检查后，取网格总数约为6万。入口为速度入口，出口用出流条件，上、下壁面及圆柱表面为无滑移壁面条件。流体介质为可压缩空气，密度ρ=1.225 kg/m3，动力粘度ν=1.789×10-5kg/（m·s），雷诺数Re=ρu0D/ν，流场参考压强为1 atm。

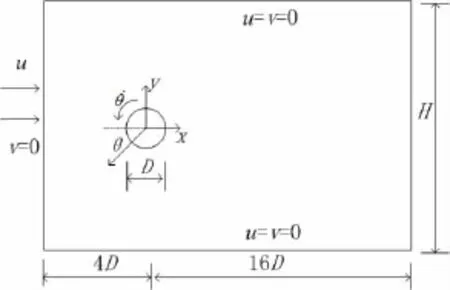
图1 计算区域示意图Fig.1 Schematic diagram of computational domain

2 数值验证

首先对Re=1.4×105条件下的非旋转圆柱绕流进行数值验证。该雷诺数时圆柱表面边界层附近为层流，当流体在圆柱表面流过时，层流边界层分离，产生旋涡脱落，上下两涡相继脱落，构成典型圆柱尾流结构。

图2为圆柱绕流涡脱落一个周期的涡量变化等值图。可知，这与经典圆柱绕流的涡脱落相同[1-2]，边界层上下分离区形成的旋涡周期性交替脱落，在尾流区形成反向的涡对，显示了后缘涡交替脱落的非定常过程。当空气流向圆柱时，在圆柱迎风面的前缘形成了一个滞止点（驻点）。从驻点开始流动逐渐加速，在顺压梯度的作用下边界层开始在圆柱上发展。当气流流经圆柱的两侧时，由于逆压梯度的作用，流体在圆柱的上下表面开始分离，形成旋涡。

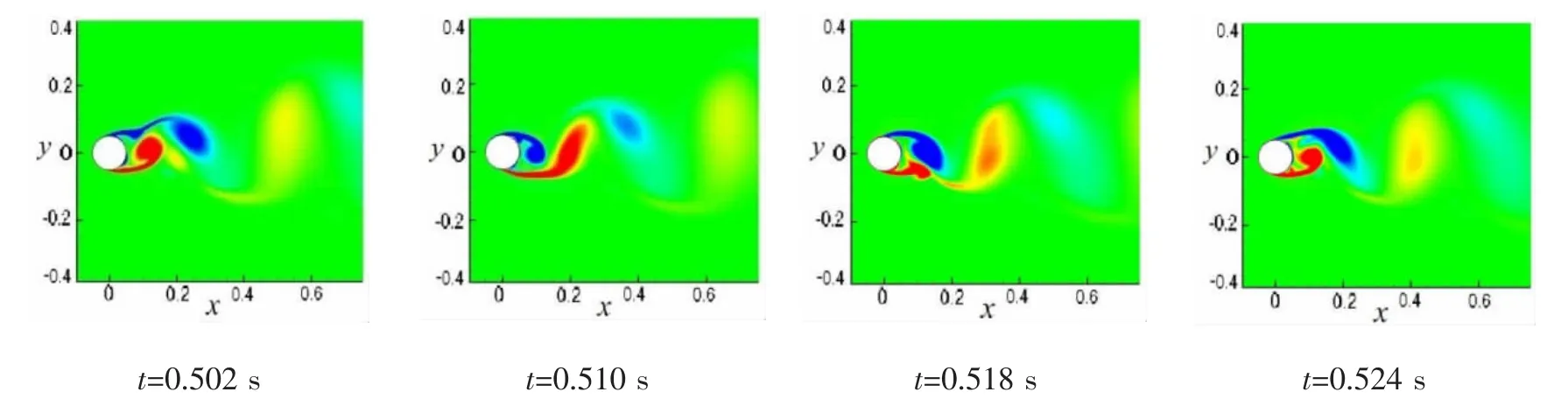
图2 圆柱绕流涡脱落的周期变化Fig.2 Periodic variation for vortex shedding of flow past a cylinder

表1为圆柱的升力系数、平均阻力系数与Strouhal数的实验结果与本文数值计算结果的对比。从表中可以看出，本文计算得到的涡脱落频率Strouhal数为0.205，与Zdravkovich等[12]的实验结果和Breuer[10]的计算结果吻合较好；平均阻力系数为1.26，与Cantwell[11]以及Zdravkovich等实验结果也较为吻合，最大偏差仅为4.76%，而与Tutar[13]的数值模拟结果偏差较大，达到11.1%；升力系数与赫鹏[10]的模拟结果基本相同。

表1 计算结果与实验结果比较Tab.1 Experimental and numerical results compared to the present ones

图3为中轴线y=0上沿来流方向的无量纲时均速度分布，此处时均值是指计算收敛到计算终止的时均值。由图3可知，回流区最小流速umin/u0=-0.05，与Breuer[10]的计算结果相比稍有偏大，尾流的速度恢复与Cantwell[11]等的实验结果相比稍快，但变化趋势保持一致。图4和图5为沿直线x=D上顺气流方向和垂直来流方向的无量纲时均速度分布，可以看出本文的计算结果与文献[10，11]总体趋势一致，且与实验结果误差范围在6%以内，因而具有可信度。

图3 沿中线y=0上u方向时均速度Fig.3 Time-averaged streamwise velocity u along the symmetry line y=0

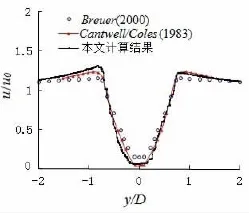
图4 沿x=D上u方向时均速度Fig.4 Time-averaged streamwise velocity u along a constant x-position x=D

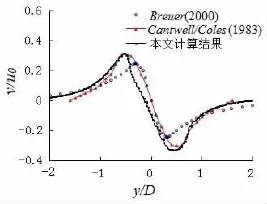
图5 沿中线x=D直线上的v方向时均速度Fig.5 Time-averaged normal velocity v along a constant x-position x=D

图6 时均稳态压力系数周向分布Fig.6 Time-averaged pressuer coeffcient Cp computed along the cylinder’s surface

3 结果与讨论

利用上述数值方法对雷诺数Re=1.4×105，圆柱转速分别为α=0.5，1.0，1.25，1.5与2.0的绕流进行数值模拟。图7为各不同转速条件下，圆柱绕流的瞬时流线。图8为转速α=1.5条件下，圆柱绕流典型周期变化时的涡量等值分布。

从图7中可以看出，当圆柱不旋转时，流体在圆柱顶端分离，圆柱上、下表面的分离点S1和S2的位置基本相同，各自在一定范围内随着上下表面涡的脱落而产生摆动。当圆柱旋转后，因流体粘性作用，圆柱表面流体随圆柱以相同转速运动，因而圆柱下方的圆周速度与来流速度叠加，流速加快，而上方圆周速度与来流速度方向相反，使其总流速下降。对于α=0.5，此时虽然圆柱旋转速度不大，但上表面分离点S1向前移动，而在下表面区域，旋转边界层内的流体速度被加速，逆压梯度出现较后，因此边界层内分离点S2较无旋转时靠后，同时，分离产生的涡开始向尾部偏上区域发展。随着转速的进一步增加，圆柱下表面流体圆周速度进一步加大。当α=2时，旋转边界层远大于自由流速平均值，圆柱下表面分离点则向圆柱尾部转移，接近后驻点位置才从壁面脱落，而圆柱上表面分离同样变得不明显，且尾部回流区域变小。

图7 Re=1.4×105时，不同转速条件下的瞬时流线图Fig.7 Instantaneous streamlines of velocity field for different spin ratio at Re=1.4×105

图8 Re=1.4×105时，转速α=1.5条件下的涡量周期变化分布Fig.8 Periodic variation for vorticity distributions of flow past a cylinder for α=1.5 at Re=1.4×105

由图8可知，转速α=1.5时，旋涡在圆柱右上方交替脱落，此时脱落的涡和非旋转时相比变小，且涡街脱落不再上下对称，而是向上偏移并和x轴成一定角度。

图9为不同转速时的湍流动能等值云图。可知，在亚临界条件下，圆柱周围的湍流动能值很低，圆柱表面边界层附近为层流，随着涡街的脱落，在圆柱下游出现一个高湍流动能区域，脱体涡开始湍流转捩。对于不旋转圆柱，其尾部附近的湍流动能基本对称，大概在x=1.3D左右达到最大值；随着圆柱转速的增加，圆柱尾部湍流区域开始变小，且随着涡的上移而向上转移，另外，湍流动能值随圆柱旋转速度的增大而变小。

由此可知，圆柱旋转可有效抑制圆柱表面边界层的分离，降低分离涡的大小以及抑制尾部湍流产生。

图10为Re=1.4×105时，不同转速时圆柱阻力和升力系数的时间变化曲线。可知，对于α≤1.5，升力系数在整个监测时间内都以高幅值多周期振荡，随着转速的增加，幅值逐渐下降；α=2时，在一段时间内波动幅值不规律，流体依然是非稳态的，经过一个短暂的过渡时间后升力系数和阻力系数都变小，且趋于稳定单周期性振动，表明此时圆柱表面涡的脱落呈现稳定的单周期性。

图9 Re=1.4×105时，圆柱不同转速时的湍流动能分布Fig.9 Contours of the total resolved kinetic energy of the fluctuations for different spin ratio at Re=1.4×105

图10 Re=1.4×105时，不同转速时的阻力系数和升力系数历时曲线Fig.10 Time histories of the drag and lift coefficient for different spin raito at Re=1.4×105

图11为Re=1.4×105时，不同转速条件下圆柱表面平均压力系数分布。由图可知，随着α的增大，圆柱下表面因边界层速度增加，导致其压力降低，且降低辐值受转速增加而增加，在圆柱下表面最低处（θ=90°）左右达到最小。相比圆柱下表面，圆柱上表面压力随转速的变化不大。

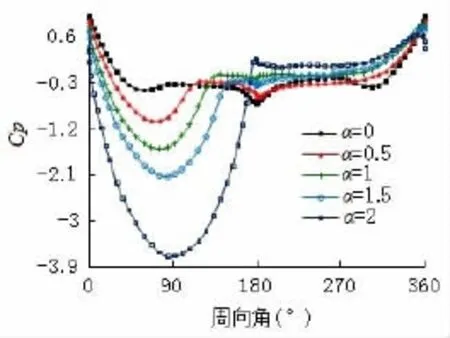
图11 不同转速的圆柱表面时均压力系数周向分布Fig.11 Time-averaged pressuer coeffcient Cp computed along the cylinder’s surface for different spin ratio

图12和图13分别为不同雷诺数Re=160，6×104，1.4 105时，不同转速条件下的阻力系数和升力系数变化曲线由图12可知，阻力系数随α的增大而降低；由图13可知转速为0时，由于圆柱上下表面的压力变化的平均值基本对称，所以升力为0，圆柱逆时针旋转时，下表面边界层内速度增加，而上表面速度减小，导致圆柱上表面压力大于下×。，表面的压力，从而产生向下的侧向力（负升力），且随着转速增加，升力系数绝对值增大，曲线变陡。

图12 时均阻力系数随转速变化规律Fig.12 Mean drag coefficient versus spin raito for different Re

图13 时均升力系数随转速变化规律Fig.13 Mean lift coefficient versus spin raito for different Re

4 结论

本文采用LES方法对亚临界区典型雷诺数（Re=1.4×105）条件下，不同旋转速度的圆柱绕流进行了数值研究。首先，通过对非旋转圆柱绕流的数值模拟，计算所得升力系数、阻力系数以及Strouhal数等均与相关研究成果符合，表明本文计算方法可以模拟复杂的非稳态流场结构。

通过对旋转速度在0-2之间的圆柱绕流特性进行模拟，发现随着转速的增加，圆柱下表面流体分离点则向尾部转移，直到接近后驻点位置，而圆柱上表面分离同样变得不明显，分离涡变小，且涡街脱落不再上下对称，而是向上偏移并和x轴成一定角度。另外，随着圆柱旋转速度增加，圆柱尾部回流区域同样变小，且湍流区域变窄以及湍流动能降低，圆柱阻力与升力的振幅降低，且阻力值较无旋转时变小，而升力的绝对值增加，这主要是因为圆柱逆时针旋转时，下表面边界层内速度增加，而上表面速度减小，导致圆柱上表面压力大于下表面的压力，从而产生负升力，且随着转速增加，升力系数绝对值增大。

[1]陈志华,范宝春.包覆电磁场激活板的圆柱尾迹的数值研究[J].力学学报,2002,34(6):978-983. Chen Zhihua,Fan Baochun.Numerical investigation on wake of cylinder covered with electro-magnetic actuator[J].Acta Mechanica Sinica,2002,34(6):978-983.

[2]张辉,范宝春,陈志华.电磁力控制下圆柱绕流的涡度拟能[J].应用数学和力学,2008,29(11):1365-1375. Zhang Hui,Fan Baochun,Chen Zhihua.Evolution of global enstrophy in cylinder wake controlled by Lorentz force[J]. Applied Mathematics and Mechanics,2008,29(11):1365-1375.

[3]Kang S,Choi H.Laminar flow past a rotating circular cylinder[J].Physics of Fluids,1999,11(11):3312-3321.

[4]Ingham D B,Tang T.A numerical investigation into the steady flow past a rotating circular cylinder at low and intermediate Reynolds numbers[J].comput.Phys.1990,87:91-107.

[5]Kang S.Laminar flow over a steadily rotating circular cylinder under the influence of uniform shear[J].Phy.Fluids.,2006, 18(4):1-12.

[6]Mittal S,Kumar B.Flow past a rotating cylinder[J].Journal of Fluid Mechanics,2003,476:303-334.

[7]Padrino J C,Joseph D D.Numerical study of the steady-state uniform flow past a rotating cylinder[J].Journal of Fluid Me chanics,2006,557:191-223.

[8]赫鹏,李国栋,杨兰等.圆柱绕流流场结构的大涡模拟研究[J].应用力学学报,2012,29(4):437-443. Hao Peng,Li Guodong,Yang Lan,et al.Large eddy simulation of the circular cylinder flow in different regimes[J].Chinese Journal of Applied Mechanics.2012,29(4):437-443.

[9]Isiam W S,Raghavan V R.Numerical simulation of high sub-critical Reynolds number flow past a circular cylinder[C]. Int.Conference on Boundary and Interior Layers.,2006.

[10]Breuer M.A challenging test case for large eddy simulation:High Reynolds number circular cylinder flow[J].International Journal of Heat and Fluid Flow,2000,21:648-654.

[11]Cantwell B,Coles D.An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder [J].Journal of Fluid Mechanics,1983,136:321-374.

[12]Zdravkovich M.Flow around circular cylinders[M].England:Oxford University Press,1997.

[13]Tutar M,Holdob A E.Computational modeling of flow around a circular cylinder in sub-critical flow regime with various turbulence models[J].International Journal for Numerical Methods in Fluids,2001,35(7):763-784.

Flow field characteristics of flow past a rotating cylinder

HE Ying1,YANG Xin-min1,CHEN Zhi-hua1,LIU Bo2,YI Wen-jun1
(1.Key Laboratory of Transient Physics,Nanjing University of Science&Technology,Nanjing 210094,China; 2.Huai-hai Industry Group Co.,Ltd.,Changzhi 046012,China)

Under the sub-critical condition withRe=1.4×105,flow past a rotating cylinder with uniform inflow is simulated numerically with Large Eddy Simulation(LES).The results are verified accurately through the comparison of the corresponding experimental and simulated results of the non-rotating case.Furthermore, flow past a rotating cylinder with different spin ratios(0≤α≤2,αis the ratio of the cylindrical circumferential speed to the free-stream speed).The numerical results show that the rotation of the cylinder can suppress vortex shedding effectively,and with the increase of spinning ratio,the mean drag coefficient of cylinder decreases while the lift coefficient increases.The amplitude of mean drag and lift coefficients become steady through a short transitional period forα=2.

High Reynolds number;rotating cylinder;flow past a cylinder

O35

A

10.3969/j.issn.1007-7294.2015.05.004

1007-7294（2015）05-0501-08

2014-11-24

校自主专项（2010XQTR05）

何颖（1987-），女，博士研究生，E-mail：279335082@qq.com；

杨新民（1959-），男，副研究员；

陈志华（1967-），男，教授。