浅水超临界航速舰船水压场数值计算
2015-04-26邓辉张志宏刘巨斌顾建农
邓辉,张志宏,刘巨斌,顾建农
(海军工程大学理学院,武汉430033)
浅水超临界航速舰船水压场数值计算
邓辉,张志宏,刘巨斌,顾建农
(海军工程大学理学院,武汉430033)
文章基于浅水波动势流理论和薄船假定,建立了浅水超临界航速舰船水压场理论模型。采用有限差分方法,对不同宽度航道下浅水超临界航速舰船水压场进行了数值计算。分析了航道岸壁、水深佛鲁德数、色散效应对舰船水压场的影响。通过与傅里叶积分变换法以及实验结果进行比对,表明了所建立的舰船水压场理论模型与计算方法吻合得较好。
浅水;超临界航速;舰船;水压场;有限差分法;傅里叶积分变换法
0 引言
舰船水压场是指航行舰船在水中引起的压力变化,它是航行舰船自身难以消除的物理特性,与船型、航速、水深及岸壁等多种因素密切相关。由于舰船航行引起的水压变化对岸壁、河床均有洗刷效应,且通过检测舰船水压场信号特征可以发现和识别舰船目标,多年来对它的研究一直受到国内外学者的重视。Tuck(1966)[1]基于渐近匹配展开法,得到了浅水薄船水压场的一个近似解;Müller(1985)[2]利用有限水深兴波源势方法,通过在船舶纵向剖面上布置源汇,提出了薄船、线性自由表面条件下的舰船水压场计算公式;Sahin和Hyman、Nguyen等[3-6]采用有限水深格林函数方法,系统开展了潜艇、水面舰艇和气垫船水压场的理论建模和数值计算工作;张志宏(2002)等[7-8]采用傅里叶积分变换法,得出了浅水开阔海域舰船水压场的解析解,并进行了实验研究;黎昆(2011)[9]、缪涛(2012)等[10]利用面元法计算了舰船在水底引起的压力分布。
在浅水船舶水动力学领域,水深佛鲁德数Fh是一个重要特征参数,Fh<1和Fh>1分别称为亚临界航速和超临界航速,Fh=1为临界航速。由于在临界航速附近,舰船运动将会产生特殊的前传孤立波现象,故通常也将0.8<Fh<1.2称为跨临界航速。本文基于所建立的浅水超临界航速舰船水压场理论模型,采用有限差分法对舰船在不同宽度航道航行引起的水压变化进行数值计算,并与傅里叶积分变换法以及船模实验结果进行比对,验证了该计算方法的准确性及适用性,并可为下一步开展浅水跨临界航速舰船水压场研究提供基础。
1 理论模型
1.1 控制方程
假设流体为理想不可压流体,运动无旋。取动坐标系固结于船体,坐标原点位于船体水线中心,x轴指向舰船运动方向,y轴指向海域岸壁,z轴垂直向上。设船长为L,船速恒为V,水深恒为h,自由表面起伏为ζ。运动舰船引起的流场扰动速度势φ应满足以下方程:
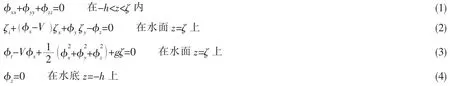
水深h≤0.3L时,可视为浅水。结合浅水波特点,引入反映色散效应、非线性效应的小参数μ=h/L和ε=A/h,并对方程式(1)~(4)进行无因次化处理,令
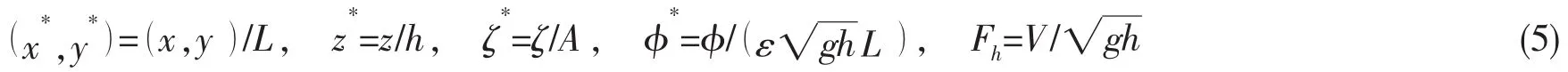
式中:带“*”为无因次量,A为波幅。

式中:第三项为非线性效应项,第四项为色散效应项。
将(6)式根据(5)式返回为有因次变量,如忽略(6)式中的非线性项,则简化为仅考虑色散效应的超临界航速浅水控制方程,即

如(6)式中的非线性项和色散项均忽略,则简化为未考虑非线性效应和色散效应的超临界航速浅水控制方程,即

1.2 船体边界条件
计算采用Wigley数学船型,船体表面方程为

采用薄船边界条件为

1.3 岸壁边界条件
当舰船在开阔海域航行时,岸壁边界条件为

当舰船在有限宽度航道中心线上航行时,岸壁边界条件为

式中:w为航道宽度。
2 计算方法
2.1 有限差分法
根据舰船超临界航行特点,采用显式差分格式对边界条件和控制方程(7)、(8)分别进行离散。沿船长方向为x方向用i标记,网格间距为Δx;沿船宽方向为y方向用j标记,网格间距为Δy。其中x方向二阶导数采用二阶精度由上游至下游的三点迎风差分格式,y方向二阶导数采用二阶精度的三点中心差分格式,而色散效应项为x方向四阶导数,根据超临界色散特点,采用从上游至下游的五点偏后差分格式,即:
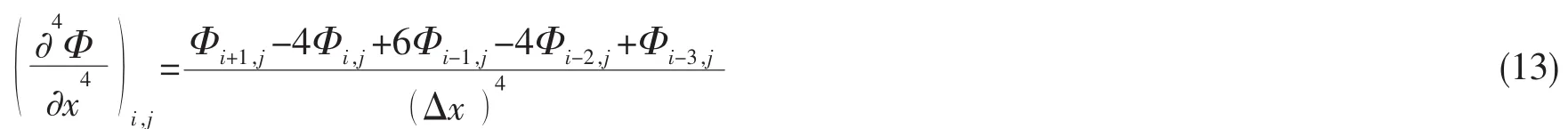
未考虑非线性效应和色散效应的超临界航速浅水控制方程(8)可离散为
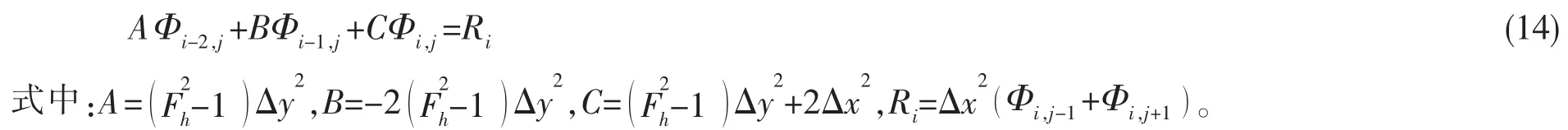
采用三对角矩阵用追赶法求解,可得离散点(i,j)处扰动速度势。
考虑色散效应的超临界航速浅水控制方程(7)可离散为
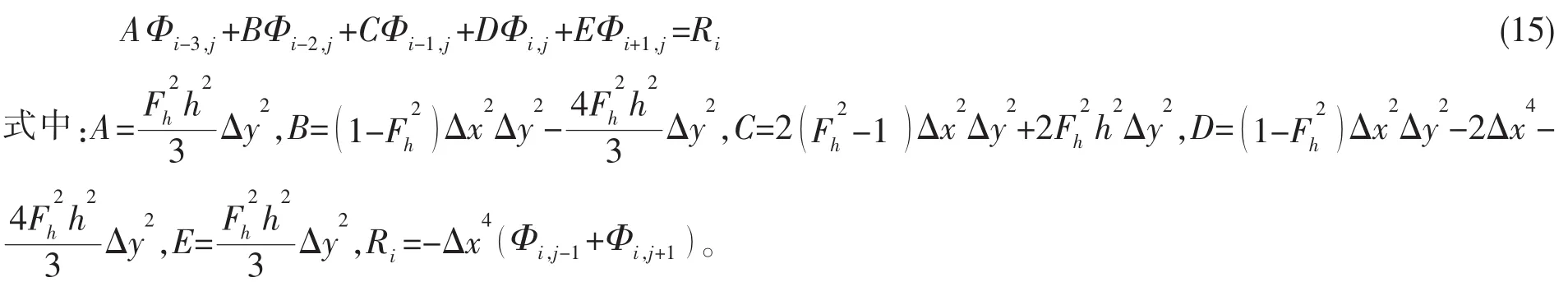
采用五对角线性方程组解法,可得离散点(i,j)处扰动速度势。
由离散点(i,j)处的扰动速度势可得压力系数为

式中:Δp为水中的扰动压力变化,ρ为水的密度。
2.2 傅里叶积分变换法
舰船在浅水开阔海域以超临界航速航行,采用傅里叶积分变换法求解由控制方程式(7)、船体边界条件式(10)以及岸壁边界条件式(11)组成的数学问题,得压力系数计算公式为

3 结果验证与分析
计算所采用的Wigley数学船型与实验船模具有相同主尺度,无因次水线长为1、船宽为0.197 9、吃水为0.052 08。计算区域选取x方向上游7L,下游7L,y方向1~20L,为与实验数据进行比较,计算结果取船艏、船艉分别位于-0.5L、0.5L处。为确保差分格式具有较高精度,将计算区域划分为网格间距Δx=Λy=0.05的均匀正方形网格。
3.1 结果验证
采用傅里叶积分变换法及有限差分法,分别计算了舰船以超临界航速Fh=1.2在开阔海域航行引起的压力变化,如图1(a)、(b)所示。结果对比表明,两种方法计算得到的压力系数三维分布特征一致,Havelock半角角度相同,峰谷对应位置吻合,验证了本文数值计算方法的有效性。尽管傅里叶积分变换法计算的压力分布结果更加精细,但由于该方法对有限宽度航道问题求解困难,故采用有限差分法具有更强适用性。
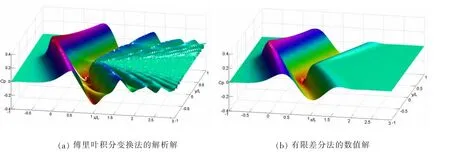
图1 开阔海域下的舰船水压场空间分布(h=0.1L,Fh=1.2)Fig.1 Three dimensional distribution of ship hydrodynamic pressure field in the open water(h=0.1L,Fh=1.2)
为进一步验证所采用计算方法的准确性,应用有限差分法计算了距舰船航线横向距离(即横距)分别为y=0、y=0.25L、y=0.5L的水压通过特性曲线,并与实验结果进行了比对,如图2所示。可以看出,计算得到的y=0、y=0.25L、y=0.5L的水压通过特性曲线均与实验结果趋势一致,船艏附近出现较大正压,船艉附近出现较大负压,且计算得到的负压系数峰值位置与实验结果基本相同;从不同横距的水压通过特性曲线可看出,横距越大,即离船体越远,压力系数峰值越小,且在x方向不断后移,但水压通过特性曲线的特性仍与舰船正下方基本一致。由于本计算采用Wigley数学船型,与实验船模存有一定差异,使得横距y=0时计算出的船艏正压系数峰值位置与实验值略有偏差。
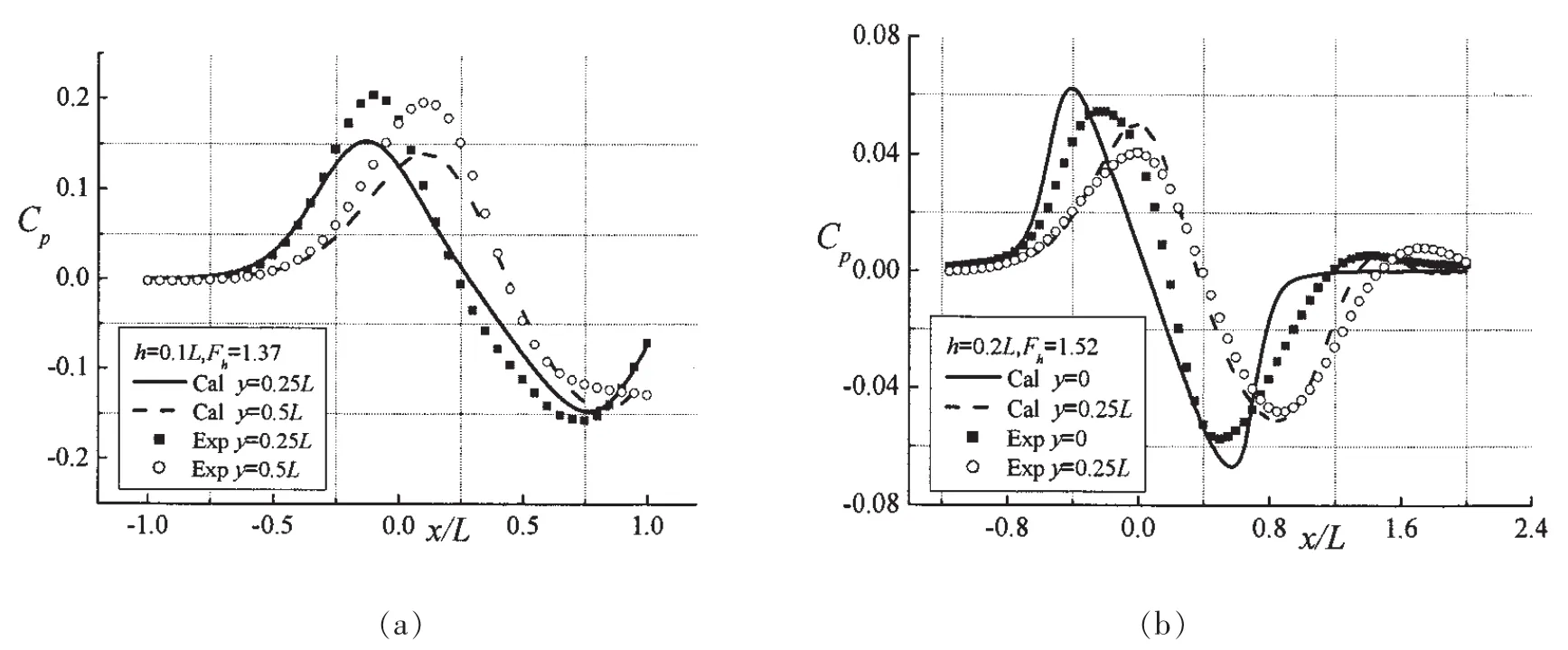
图2 超临界航速舰船水压场纵向通过特性曲线(w=4.5L)Fig.2 Longitudinal curves of pressure field caused by ship moving at supercritical speed(w=4.5L)
3.2 结果分析
3.2.1 色散效应对舰船水压场的影响
将考虑色散效应和未考虑色散效应的计算结果与实验结果进行比较,如图3所示。从图中可以看出,考虑色散效应的计算结果与实验结果更加吻合。但当Fh>1.6时,因舰船超高速航行,船体姿态发生较大变化,沾湿表面及吃水均不断改变,而本文计算未考虑船体沾湿表面变化,因而计算结果存在一定误差;当Fh=1.0~1.2时,由于存在较强的非线性效应和色散效应影响,使得计算结果与实验结果偏差较大,需进一步建立和求解计及非线性和色散效应影响的跨临界航速舰船水压场理论模型。
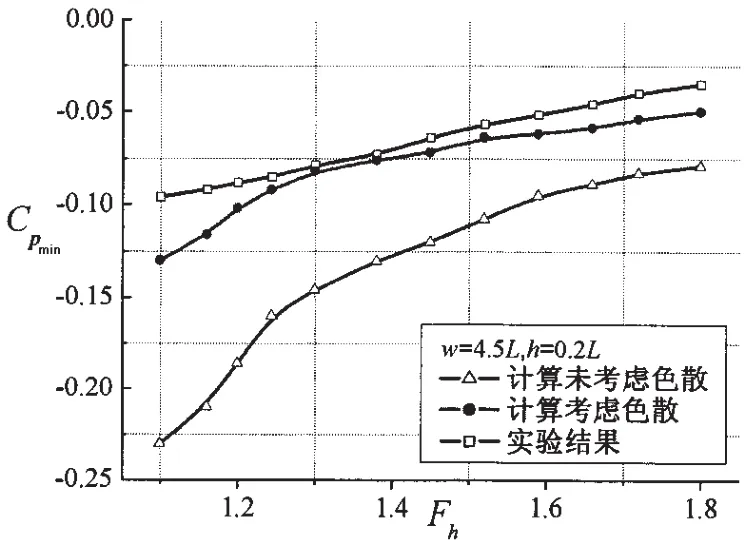
图3 负压系数峰值随水深佛鲁德数变化曲线Fig.3 The peak of negative pressure coefficient V.S depth Froude number
3.2.2 岸壁对舰船水压场的影响
为了分析岸壁对舰船水压场的影响,对h=0.1L,0.2L时,不同宽度航道下舰船航行引起的水压变化进行了计算,如图4所示。从图4(a)可看出,h=0.1L时,当航道宽度由10L减小至4.5L,舰船航行引起的负压系数峰值基本不变,即w≥4.5L,岸壁反射作用对超临界航速舰船水压场影响甚微;随着航道宽度继续变窄至w=2.0L,水深佛鲁德数Fh<1.4的负压系数峰值缓慢回升,而Fh≥1.4的负压系数峰值与开阔海域基本相同;航道宽度再次减小,岸壁反射回的压力波更加靠近船体,受航道宽度影响的航速范围进一步增大,使得水深佛鲁德数Fh<2.0的负压系数峰值均出现不同程度的回升,且越接近临界航速回升的幅度越大。
为进一步证实航道宽度的影响,图4(b)为h=0.2L,Fh=1.4时不同航道宽度的舰船水压场纵向通过特性曲线,可以看出,舰船以超临界航速航行,负压严重后移,甚至移至船艉之后;当航道宽度由4.5L减小至2.0L时,负压系数峰值基本不变,这与图4(a)得出的结果一致,但通过特性曲线在船艉之后有了明显变化,w=2.0L的船后正压系数峰值明显高于w=4.5L,岸壁反射对舰船尾部压力场扰动增大;随着航道宽度继续变窄,岸壁反射的正压与舰船自身的负压区叠加,负压系数峰值进一步回升,由于岸壁的多次反射作用,船后正压峰值和压力波动继续增大,使得船后水域受舰船水压场的影响范围持续后延。
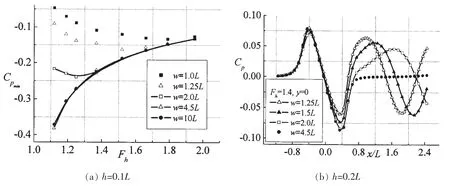
图4 舰船水压场随航道宽度的变化Fig.4 Pressure field V.S different width channel
综上分析可得,舰船以超临界航速航行时,虽然岸壁越窄,舰船水压场负压系数峰值越小,但由于岸壁反射波的作用导致舰船水压场对船后水域的影响范围增大,使得其对更广范围的岸壁及河床产生较为严重的洗刷效应。可见,航道越窄,高速航行的舰船产生的水压变化将对其后更大水域范围产生影响。
3.2.3 水深佛鲁德数对舰船水压场的影响
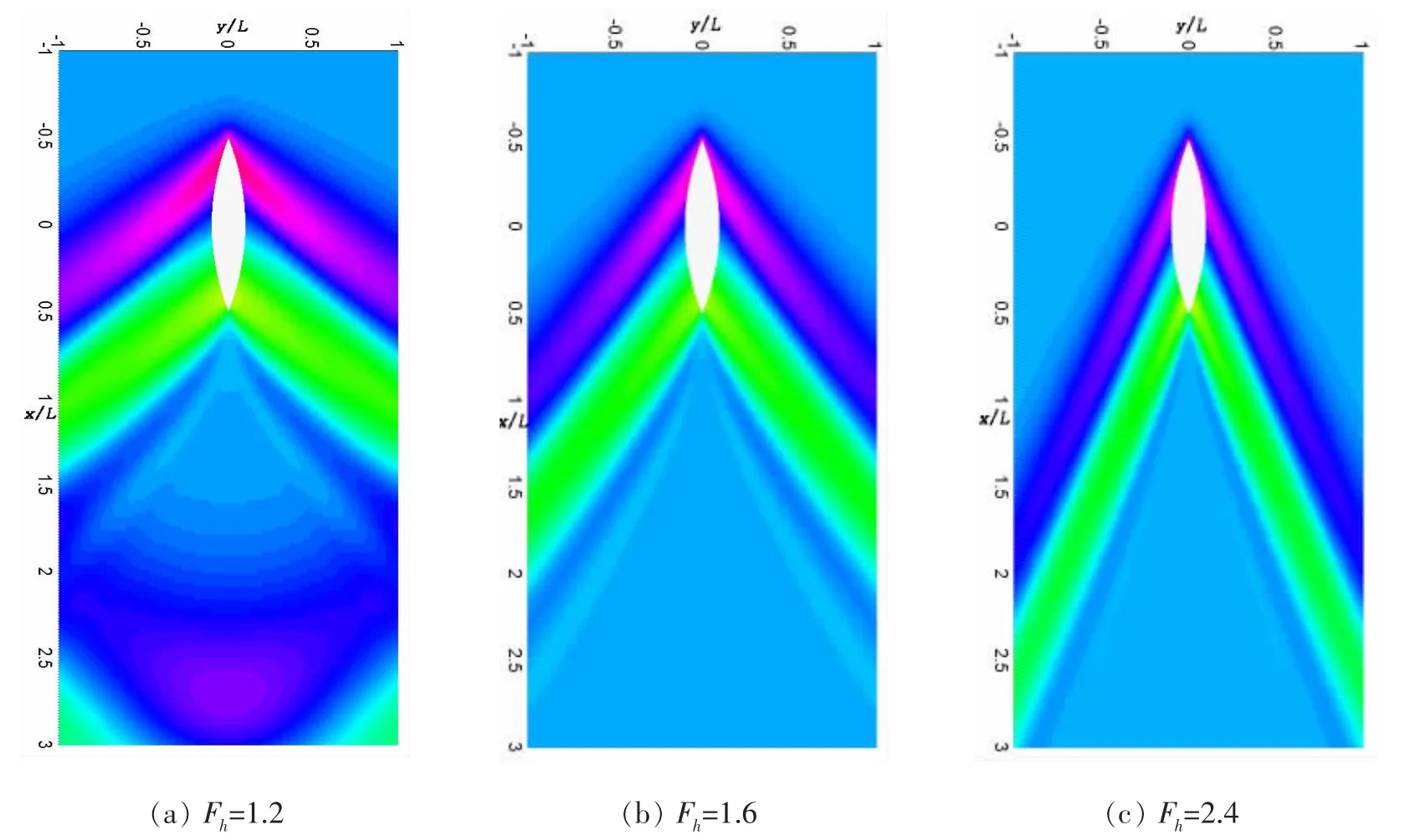
图5 舰船水压场平面分布图(w=4.5L,h=0.1L)Fig.5 Two dimensional distribution of ship hydrodynamic pressure field(w=4.5L,h=0.1L)
在w=4.5L,h=0.1L时,不同水深佛鲁德数下航行舰船引起的水压场平面分布如图5所示。当Fh=1.2时,可见岸壁反射波在船艉之后,对舰船自身水压场干扰较大,岸壁反射作用导致舰船水压场横向区域影响较严重;当Fh=1.6时,船艏艉出现“V”形散波;随着水深佛鲁德数进一步增大,舰船水压场负压区后移,岸壁反射波同时后移且对水压场的干扰减弱,“V”形散波Havelock半角随Fh增加也逐渐减小,如图6所示,采用有限差分法计算出的Havelock半角与理论值sin-1(1/Fh)变化趋势一致;当Fh→1时,“V”形散波Havelock半角接近90°,舰船航行产生的水压变化横向影响区域最广;当Fh=2.0时,Havelock半角急剧减小至30°左右,即舰船水压场在横向区域影响范围急剧变窄;随着水深佛鲁德数继续增大,Havelock半角继续减小至19°左右,减小趋势变缓。可见,水深佛鲁德数越大,舰船水压场横向影响区域越小。
综上分析可得,在一定航道宽度内,舰船以越高的水深佛鲁德数航行,产生的负压系数峰值越小,产生的压力变化横向影响区域越窄,其舰船目标信号特征越不易被检测,更有利于舰船隐身安全航行。

图6 Havelock半角(w=4.5L,h=0.1L)Fig.6 Havelock half-angle(w=4.5L,h=0.1L)
4 结论
本文应用有限差分法对超临界航速舰船水压场进行了数值计算,并与傅里叶积分变换法以及实验结果进行了比对,表明该理论模型与计算方法吻合得较好,并分析了色散效应、航道宽度以及水深佛鲁德数对超临界航速舰船水压场的影响。得到如下结论:
(1)舰船以超临界航速航行时,色散效应影响较大,不可忽略。
(2)航道宽度w≥4.5L,岸壁对超临界航速舰船水压场影响甚微;随着航道宽度变窄,岸壁反射作用导致舰船水压场对船后水域的影响范围增大,使其对更广范围的岸壁及河床产生较为严重的洗刷效应。
(3)接近临界航速,舰船水压场在横向区域影响较广。随着水深佛鲁德数增大,Havelock半角减小,负压区出现后移,舰船水压场在横向区域影响范围逐渐变窄,意味着舰船以越高的水深佛鲁德数航行,产生的负压系数峰值越小,引起的压力变化横向影响区域越窄,舰船附近引起的水压特征信号减弱,范围减小,有利于舰船隐身安全航行。
[1]Tuck E O.Shallow-water flows past slender bodies[J].J Fluid Mech,1966,26(1):81-95.
[2]Müller E.Analysis of the potential flow field and of ship resistance in water of finite depth[J].I.S.P.,1985(32):266-277.
[3]Sahin I,Hyman M C.Numerical calculation of the flow of submerged bodies under a free surface[J].Ocean Engineering, 1993,20(3):339-345.
[4]Sahin I,Hyman M C,Nguyen T C.Three-dimensional flow around a submerged body in finite-depth water[J].Applied Mathematical Modeling,1994,18:611-619.
[5]Sahin I,Crane J W,Watson K P.Application of a singularity panel method for hydrodynamics of underwater vehicles[J]. Ocean Engineering,1997,24(6):501-512.
[6]Sahin I,Hyman M C.Simulation of three-dimensional finite-depth wave phenomenon for moving pressure distributions[J]. Ocean Engineering,2001,28(12):1621-1630.
[7]张志宏,顾建农,郑学龄等.航行船舶在浅水水底引起的压力变化[J].中国造船,2002(2):9-14. Zhang Zhihong,Gu Jiannong,Zheng Xueling,et al.Pressure variation on shallow water bottom caused by moving ship[J]. Shipbuilding of China,2002(2):9-14.(in Chinese)
[8]张志宏,顾建农,郑学龄等.有限水深船舶水压场的实验研究[J].水动力学研究与进展,2002(6):9-14. Zhang Zhihong,Gu Jiannong,Zheng Xueling,et al.Experimental study of hydrodynamic pressure field caused by a moving ship in finite-water[J].Journal of Hydrodynamics,2002(6):9-14.(in Chinese)
[9]黎昆,张志宏,顾建农等.利用面元法计算舰船在水底引起的压力分布[J].海军工程大学学报,2011,23(1):43-46. Li Kun,Zhang Zhihong,Gu Jiannong,et al.Calculating pressure distribution on water bottom caused by a moving ship with panel method[J].Journal of Naval University of Engineering,2011,23(1):43-46.(in Chinese)
[10]缪涛,张志宏,顾建农等.面元法求解有限水深船舶兴波及水底压力变化[J].计算力学学报,2012,29(3):464-469. Miao Tao,Zhang Zhihong,Gu Jiannong,et al.The calculation of ship wave and bottom pressure variation in finite depth by panel method[J].Chinese Journal of Computational Mechanics,2012,29(3):464-469.(in Chinese)
[11]张志宏,顾建农.浅水高速船舶引起的波浪和压力场研究[J].船舶力学,2006,10(2):15-22. ZHANG Zhihong,Gu Jiannong.Research on wave and pressure field caused by ship moving at high speed in shallow water [J].Journal of Ship Mechanics,2006,10(2):15-22.(in Chinese)
Numerical calculation of pressure field caused by ship moving at supercritical speed in shallow water
DENG Hui,ZHANG Zhi-hong,LIU Ju-bin,GU Jian-nong
(College of Science,Naval University of Engineering,Wuhan 430033,China)
A mathematical model for pressure field caused by ship moving at supercritical speed in shallow water was established,based on the shallow water wave potential flow theory and slender ship assumption. The pressure field caused by ship moving at supercritical speed in shallow water was calculated by using the finite difference method.The effects of channel wall,depth Froude number and dispersion characteristics on the ship hydrodynamic pressure field were analyzed.The computed results were compared with the ones of Fourier integral transform method and experiment.The mathematical model and the calculation method were validated have a good agreement.
shallow water;supercritical speed;ship;hydrodynamic pressure field;finite difference method;Fourier integral transform method
U661.1
A
10.3969/j.issn.1007-7294.2015.05.003
1007-7294(2015)05-0493-08
2014-11-09
国防预研项目(513030203);海军工程大学自然科学基金资助项目(HGDQNEQJJ12002)
邓辉(1984-),女,硕士,讲师,Email:denghui8411@163.com;
张志宏(1964-),男,教授,博士生导师。
