铣头旋转分度精度分析

董跃，李再参，师如华，王丹

(1. 云南省机电一体化应用技术重点实验室，云南昆明650031;2. 云南省先进制造技术研究中心，云南昆明650031)

项目研发的自动大扭矩直角分度铣头是数控镗、铣床的重要功能部件。在高档数控机床上安装高精度、高自动化的数控旋转分度铣头，能有效地扩展机床的功能和提高生产效率。此项目设计方案充分利用配套机床主轴的动力源，为铣头自动精确分度和切削加工提供动力。为了满足配套各种镗铣床的要求，面对配套主机的传动系统齿轮为常规精度等级、传动链较长等问题，需对铣头与配套主机的传动系统精度进行理论分析和试验检测，以检验设计方案在分度和精度自身校正方面是否满足实用要求。

1 影响精密机械设备精度的因素

根据影响误差的因素不同，通常将误差分为3类:第一类原理误差为可分为方案误差、机构原理误差、光路原理误差和电器部分原理误差等;第二类制造误差包括零件制造误差及零部件和产品的装配调整误差;第三类使用误差为受力变形、热变形、振动及磨损等引起的误差。

当产品由光、机、电三部分构成时，这3 个部分的误差总和为总误差，总误差可分为随机误差和系统误差二大部分，随机误差主要是制造、使用等方面的误差;系统误差主要由原理误差和相关联的制造和使用等各种误差组成。在此项目中，根据实际情况，铣头传动系统的误差主要是随机误差，因此，下面将对随机误差进行理论分析。

2 随机误差的合成

若产品的随机性原始误差的标准差为σ1、σ2、…、σi，根据方差运算规则，合成后随机误差的标准差为:

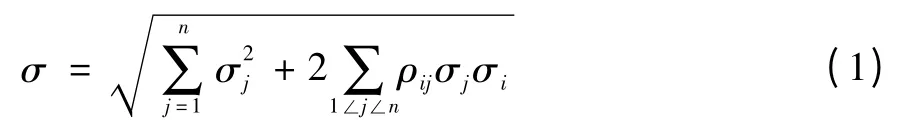
式中:ρij为第i 个和第j 个单次随机误差的相关系数。通常用极限误差δj表征随机误差，即:δj= κj·σj，系数κj不但与置信概率有关，并且与对应的随机误差的概率分布有关。常见的分布有正态分布、均匀分布和三角形分布等。合成后当各误差项互不相关，ρij=0 时，总随机不确定度极限值为:

式中:系数κ 为总随机误差的极限误差δ∑与标准误差σ 的比值，它与置信概率(置信度)和概率分布有关。

对于随机误差常常仅已知其估计值为±δj，而不知其概率分布。然而误差的分布不同，直接影响误差的合成，因此需要对未知的误差分布作出合理的假设，以使误差的合成结果最接近于真实情况。根据不同分布、不同合成方法比较，未知分布的误差假设为均匀分布较为合理，也比较保险，计算时可采用较方便的高斯算法:

3 齿轮传动的精度计算

在铣头分度旋转中，传动齿轮制造和装配的不确定会影响传动系统的传动精度，例如:齿轮有径向圆跳动和轴向窜动，轴与孔有配合间隙，铣头箱体有孔距误差、导向面误差等。传动件的误差最终将在不同程度上影响整个传动系统的传动精度。在使用过程中，作用力及温度的变化也会影响传动链的传动精度。传动精度可分别从传动误差和回程误差两个方面进行研究。

在该铣头传动系统中，旋转分度的动力主要来源于配套主机伺服电机的动力，通过齿轮传动链实现传递的。因此，下面将重点对齿轮副的传动误差进行分析计算。

齿轮传动链的传动误差是各对齿轮副传动误差的综合，而每对齿轮副传动误差则是由齿轮、轴、轴承和箱体孔的制造及其装配误差、受力变形等造成的。

3.1 影响齿轮传动误差的因素

3.1.1 齿轮加工误差

影响齿轮传动误差的主要因素是齿轮加工误差。由齿轮公差标准可知，根据齿轮传动的用途和生产条件，齿轮的运动精度可任选下列一组检验来验收:

(2)周节累积公差(Fp)(静态综合精度指标);

(4)齿圈径向跳动公差(Fr)与公法线长度变动公差(Fw)。

设想引入一个随机变化的由几何偏心和运动偏心综合而成的当量偏心eΣ，则由此偏心造成的那部分传动误差(在齿轮节圆上度量的线值)可表示为:

3.1.2 齿轮孔与轴的配合间隙及轴偏心

由间隙、轴偏心引起的传动误差表达式分别为:

Δc= Δc·sinφc/2cosα

Δs= Δs·sinφs/2cosα

式中:Δc 为轴孔配合间隙;Δs 为轴的径向圆跳动;φc为间隙偏心的相位角;φs为轴偏心的相位角。

单个齿轮传动误差的标准差σt为:

3.2 传动误差的传递与综合

图1 所示的传动链，在输出轴l 上的传动链传动误差Δtl为各个齿轮传动误差折算到输出轴l 后的综合。传动链传动误差的综合式为:

式中:Δtk为第k 个齿轮的传动误差， (');ikl为第k个齿轮到输出轴l 的转速比，ikl=nk/nl;Δtk、Δtl均为随机误差。因此，在输出轴l 上的传动链传动误差，根据式(2)和式(3)得统计值计算式:

式中:σtl为输出轴l 上的传动链传动误差的理论标准差(');σtk为第k 个齿轮传动误差的标准差(')。

图1 传动链示意图

4 铣头工作原理

图2 是滑枕式镗铣床与铣头配套的传动系统示意图，铣头通过滑枕主轴的端键将动力传递给铣头固定轴。铣头功能部件在液压油驱动下，通过运动壳体的左、右移动，实现了以下二种工况:

向右移动时，固定轴外齿圈Z17与运动壳体内齿圈Z16啮合，而联接运动和固定壳体的端齿盘脱啮，运动壳体在固定轴的带动下实现旋转分度;

向左移动时，齿轮Z17与Z16脱啮，而固定和运动壳体的端齿盘啮合，运动壳体被牢固锁紧，确保铣头切削中具有足够的刚度;同时，还利用端齿盘自身的分度精度对铣头运动壳体的旋转分度误差进行精确校正;另外，固定轴Z18与铣头主轴Z19伞齿轮的啮合，滑枕主轴带动铣头主轴旋转，为铣头切削工作提供了动力。

图2 铣头与配套滑枕式镗铣床的传动系统示意图

选用D400Z 144 TED ISA 型号的端齿盘，齿数144，每齿分度2°30'，啮合示意见图3，只要旋转误差得到控制，传动链自动分度误差小于端齿半个齿的分度误差，即1°15'。端齿盘能够正常啮合，利用端齿盘自身的分度精度，就能消除铣头旋转分度时传动链产生的误差。

图3 端齿盘齿啮合示意图

5 传动系统误差计算

根据项目设计情况，传动链各孔与轴的配合都很紧，轴加工精度较高，轴的径向圆跳动很小，即δc≈0、δs≈0，则单个齿轮传动误差的标准差为:

Z8、Z9、Z11、Z12、Z16、Z17为内、外齿轮离合器，啮合精度较高，传动误差忽略不计;Z3过桥轮为变位齿轮，Z9、Z10和Z11是三联滑移齿轮，在轴Ⅲ上由花键联接传递扭转动力。传动路线分3 条为:

第1 条齿轮传动链传动误差Δtl计算列表见表1。第2 条齿轮传动链传动误差Δtl计算列表见表2。第3条齿轮传动链传动误差Δtl计算列表见表3。

表1 第1 条齿轮传动链传动误差Δtl计算

表2 第2 条齿轮传动链传动误差Δtl计算

表3 第3 条齿轮传动链传动误差Δtl计算

6 实际精度检测

6.1 测量装置

图4 铣头分度精度测量示意图

铣头壳体上有一基准孔与主轴分度轴线重合，把多齿台安装在铣头壳体的基准孔内，使多齿台回转轴线与铣头分度轴线重合。如图4，使用CZ-3 激光数显自准直仪进行测量。

6.2 测量数据

根据理论计算得知，第2 传动链传动误差Δtl值最大，因此，下面针对这一传动链，进行了铣头分度精度测量，记录见表4。

6.3 测量结果

齿盘未啮合时第2 传动链传动最大误差为5.5';齿盘啮合时最大误差为1.5″。

7 结论

通过理论计算第2 传动链传动最大误差为4.3'，实测为5.5'，实测值大于理论计算值，有可能是机床主轴长期切削工作，齿轮有一定的磨损所至。另外，为了计算方便，忽略对误差计算影响很小的传动链各孔与轴的配合、轴加工精度、轴的径向圆跳动等也会造成理论计算与样机实测的误差。

系统传动链传动最大误差只有允许误差的1/14左右，有足够精度能确保铣头的正常分度，当端齿盘正常啮合后，利用端齿盘自身的分度精度，啮合齿盘测量最大误差为1.5″，完全消除了铣头旋转分度时传动链产生的误差，该铣头设计方案是可行和实用的。

［1］史习敏．精密机械设计［M］．上海:上海科学技术出版社，1988．

［2］金泰义．精度理论与应用［M］．合肥:中国科学技术大学出版社，2005．

［3］费业泰．误差理论与数据处理［M］．北京:机械工业出版社，1987．

［4］毛英泰．误差理论与精度分析［M］．北京:国防工业出版社，1982．

［5］林洪华．动态测试数据处理［M］．北京:北京理工大学出版社，1996．

［6］机械设计手册编写组．机床设计手册［M］．北京:机械工业出版社，1978．

［7］韦恩．R．穆尔．机械精度基础［M］．北京机床研究所，译．北京:国防工业出版社，1977．